黏土中海底管线自沉过程CEL有限元法分析

霍知亮， 闫　玥， 李　嘉,3， 闫澍旺,3

(1. 天津市市政工程设计研究院， 天津 300051; 2. 天津大学 建筑工程学院， 天津 300072; 3. 天津大学 水利工程仿真与安全国家重点实验室， 天津 300072)



黏土中海底管线自沉过程CEL有限元法分析

霍知亮1， 闫玥2， 李嘉2,3， 闫澍旺2,3

(1. 天津市市政工程设计研究院， 天津 300051; 2. 天津大学 建筑工程学院， 天津 300072; 3. 天津大学 水利工程仿真与安全国家重点实验室， 天津 300072)

在深水区域，海底管线常直接铺设到海床之上，使得海管在铺设过程中下沉至泥面以下一定深度。准确预测管线安装后的埋深是评价管线侧向稳定性的关键所在，通过CEL有限元法，对海底管线自沉问题进行研究，得到无重均质黏土和有重正常固结黏土中海管下沉阻力和下沉位移之间的关系。研究表明，CEL有限元法的计算结果与理论解符合程度较好，对模拟管土相互作用问题有很好的适用性，可有效分析海底管线与土体之间的大变形问题。

海底管线；管线自沉；理论解；耦合欧拉-拉格朗日方法

0　引言

海底管线是海洋油气开发的重要组成部分，在深水区域，海底管线无需保护，故不采用挖沟或者掩埋的方式，而是直接铺设到海床之上。通常，对于典型的单孔海底管线，在铺设过程中其下沉深度约为管线直径的1/10～1/2[1]。在海底管线输送石油和天然气的过程中，需要施加一定的温度和压力，温度与压力的共同作用使管线中产生附加应力。由于受到地基土的约束，管线无法自由变形释放应力，当累计的应力值超过地基土体对管线的约束力时，管线就会发生屈曲(pipe buckling)或者移动(pipe walking)。管线的自沉深度是确定管线侧向抗力和分析管线在位稳定性的重要参数。

对于海管竖向下沉方面的研究中，Murff和Aubeny等[2，3]根据塑性解，把土体视为刚塑性的Tresca材料，得到预埋管线(wished-in-place， WIP)归一化竖向力V/Dsu和归一化下沉位移w/D之间的关系。Merifield[1]、Randolph和White[4]也研究得出在WIP情况下，管线下沉深度和土体抗力的关系，同时考虑了海管受到竖向力和水平力联合作用时V-H包络面的特性。然而Cathie[5]指出，在海管下沉过程中， 土体的隆起将导致下沉阻力大于WIP的情况，海管的自沉过程实际上是海管逐渐挤入到土体中的过程(push-in-place， PIP)，如图1所示。对于此种情况尚无精确的理论解，通常采用数值模拟的方法对PIP情况进行研究。White等[6]采用网格重划分和插值技术(Remeshing and Interpolation Technique with Small Strain Model， RITSS)对海管的PIP情况进行分析。Wang和Chatterjee[7，8]结合了应变速率和应变软化模型，采用RITSS方法对PIP情况管线下沉深度和土体抗力的关系进行探讨。

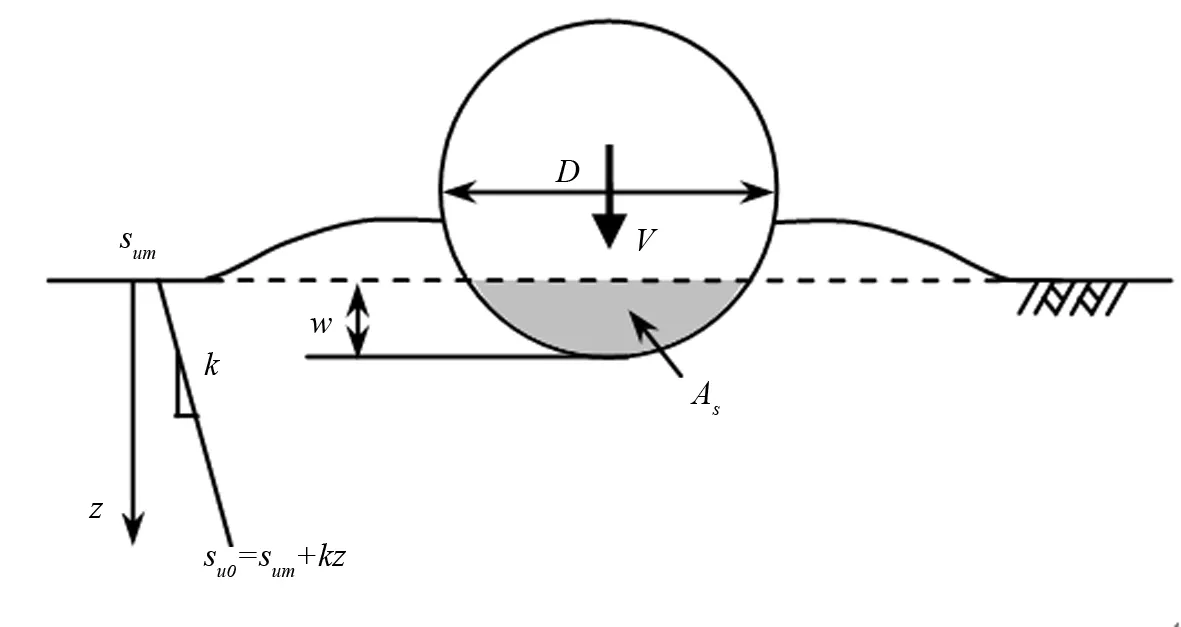
图1　管线自沉示意图

该文采用耦合的欧拉-拉格朗日(CEL)有限元法对海底管线自沉的PIP情况进行研究，得到无重均质黏土和有重正常固结黏土中海管下沉阻力和下沉位移之间的关系，探讨了容重和不排水抗剪强度随深度增加情况下海管自沉阻力的影响。研究结果还表明，CEL有限元法模拟管土相互作用问题有很好的适用性，可有效模拟海底管线与土体之间的大变形问题。

1　海管下沉阻力的理论解

准确预测管线安装后的埋深是评价管线侧向稳定性的关键所在。在均质或不排水抗剪强度随深度增加的黏土中，有许多学者根据传统的承载力理论，通过修正基础形状，提出管线竖向抗力的塑形理论解[1-4,9]，其表达形式为：

(1)

(2)

式中：V为管线单位长度的竖向荷载；D为管线的外径；su0为管线下沉深度位置的土体不排水抗剪强度；Nc为承载力系数；fb为浮力系数。根据阿基米德原理，浮力系数fb= 1，然而Merifield[9]、Randolph和White[10]的研究表明，由于管线下沉过程中土体会产生隆起，此时浮力系数fb取为1.5更适宜；As为管线下沉的截面积，其计算公式为：

(3)

(4)

式中：w为管线的下沉深度。在现有的研究中，Nc值大多忽略了土体隆起和土体重度的影响，并假定管线预埋至土中。由此可看出，土体自重和土体隆起对竖向荷载的影响体现在式(1)中的Nb项。Nc与管线的下沉深度有关，通常简化为幂函数的形式[1,3,9]，其表达形式为：

(5)

式中：a、b为拟合系数，与管土接触面的粗糙程度以及kD/sum有关。系数a和b的取值见表1，其中kD/sum= 0，表示均质土；kD/sum= ∞，表示不排水抗剪强度随深度呈三角形增长；kD/sum= 0～∞，表示不排水抗剪强度随深度呈梯形增长。

表1　w/D < 0.5时，a和b的取值

2　海管下沉CEL法分析

2.1CEL有限元法基本原理

耦合的欧拉-拉格朗日(CEL)有限元分析方法结合了拉格朗日网格与欧拉网格的优点，采用欧拉网格中网格固定而材料可以在网格中自由流动的方式建立模型，有效地解决了大变形和材料破坏等诸多问题。同时，通过欧拉-拉格朗日的接触算法，利用拉格朗日网格得到结构准确的应力应变响应，能够准确的模拟管线与土的相互作用[11-13]。

在耦合欧拉-拉格朗日有限元算法中，欧拉材料的体现是基于流体体积方法。在这种方法中，材料在网格中流动的轨迹是通过计算每一个单元中的欧拉体积分数(Eulerian Volume Fraction，EVF)来确定的。如果一个单元完全被材料填充，则这个单元的欧拉体积分数EVF=1；如果某个单元里没有材料，则它的EVF=0；如果一个单元中所有材料体积分数的总和小于1，则这个单元的剩余部分自动被“空”材料所占据，“空”材料既没有质量也没有强度。欧拉体与拉格朗日体之间的接触通常采用基于罚接触方法的通用接触算法离散。罚接触方法近似为硬化的压力-过盈关系，允许欧拉体侵入到拉格朗日体较小过盈量。拉格朗日网格区域内的物质与欧拉物质之间的界面通过基于罚函数方法的广义接触算法来模拟：

(6)

式中：FP为界面上对应点之间的接触力；dP为穿入深度；kP为罚刚度，其值与拉格朗日和欧拉介质材料特性有关。通用接触算法允许非常自动化的接触定义，能够自动指定接触面中的主面与从面，所以它能够很好地适用于涉及大变形的高度非线性的接触问题。

2.2无重均质土

采用CEL有限元法对无重均质黏土地基中的海管自沉进行分析计算。其中管线模拟为拉格朗日单元，由于其刚度很大，在下沉过程中变形量很小，故在分析中视为刚体。土体模拟为欧拉单元，计算区域为10D×8D，考虑海管下沉过程中的不排水特性，采用Tresca屈服准则，弹性模量和不排水抗剪强度的比值为500，即E/su= 500，泊松比为0.49。在土体上方建立高度为1.8D的空单元，用来模拟管线下沉时海床土体的隆起。管土之间的接触考虑为光滑和粗糙两种情况，有限元计算模型如图2所示。

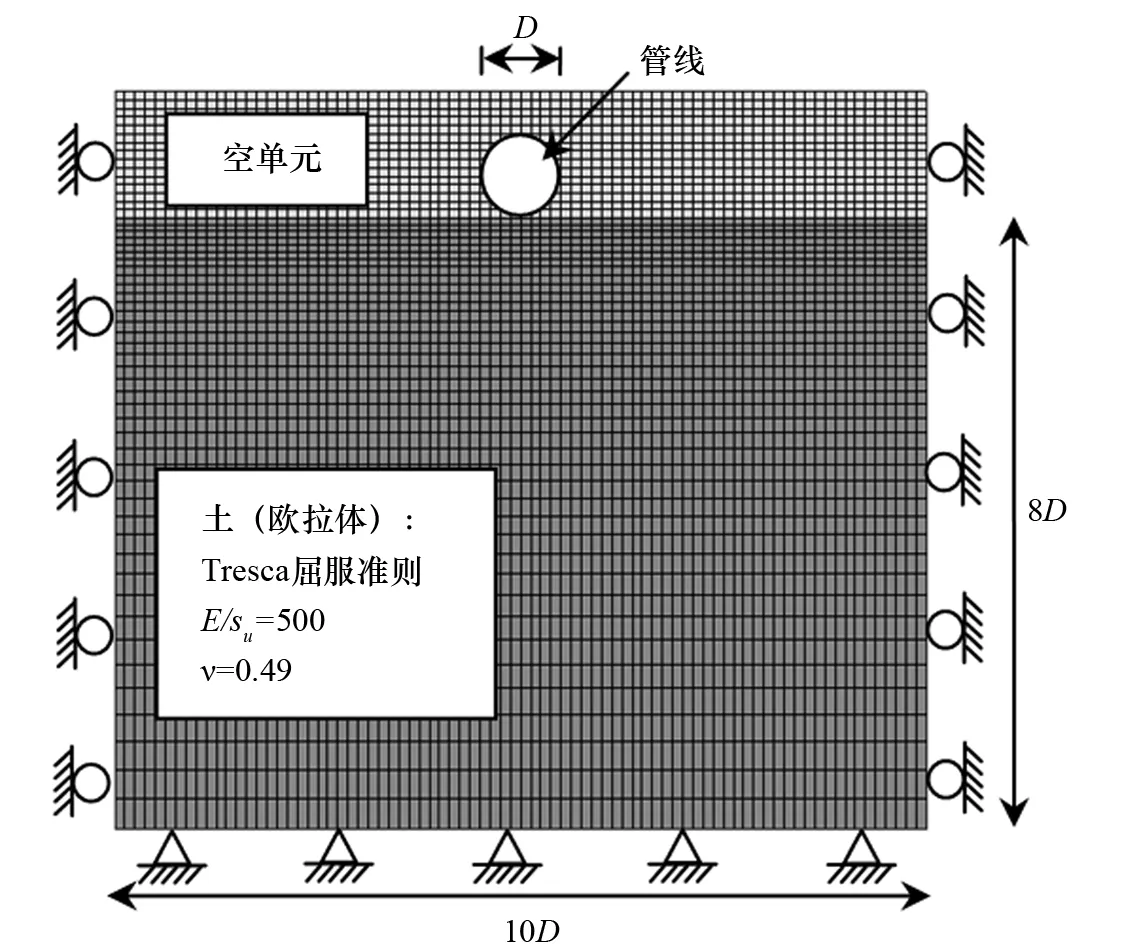
图2　有限元计算模型

对于无重土，海管下沉阻力的理论解为式(1)去除土体自重影响的Nb项，即：

(7)

参照表1中a、b的取值，对于管土粗糙接触时，a = 7.41，b = 0.37；管土光滑接触时，a = 5.42，b = 0.29。应用CEL法计算得出的结果与理论公式进行对比，计算结果如图3所示。从图3可以看出：采用CEL有限元法计算得出的归一化竖向力V/Dsu和归一化下沉位移w/D比Randolph和Houlsby[14]计算结果略小，与式(7)和Merifield[9]的计算结果十分接近，这也验证了CEL法计算结果的可靠性。

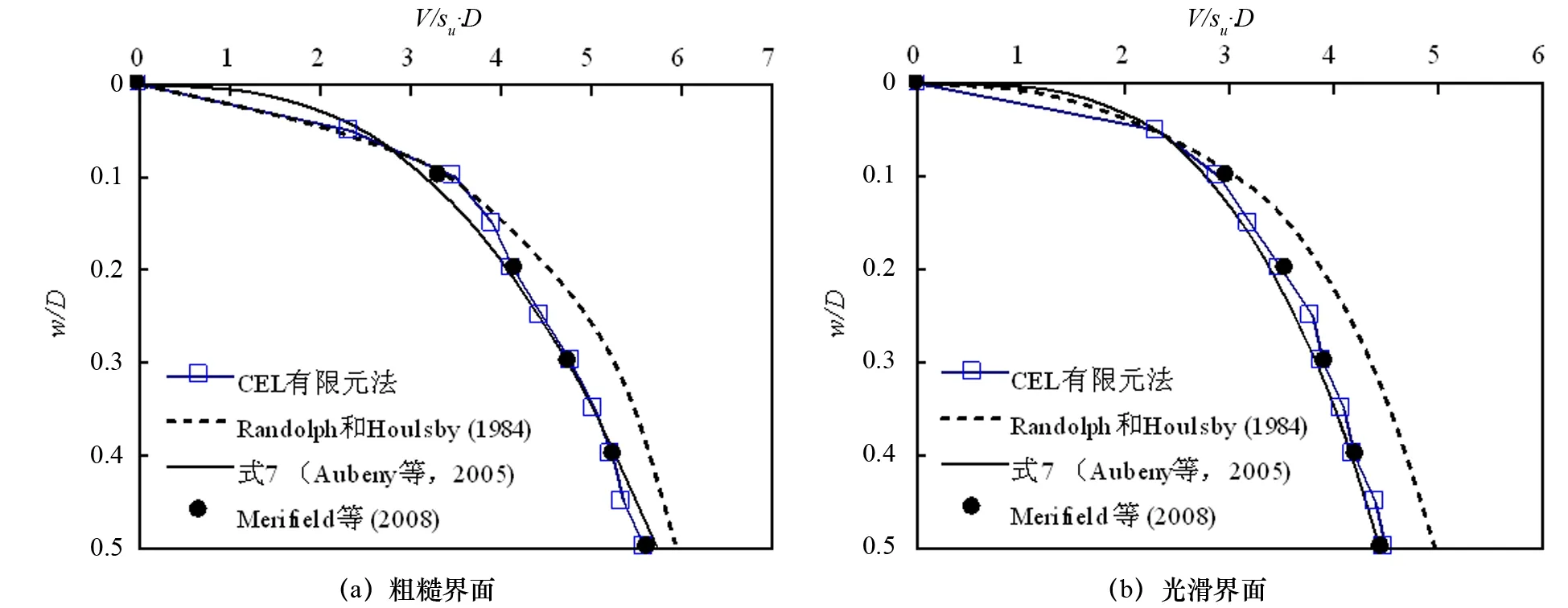
图3　无重均质土有限元计算结果

海管下沉过程中，土体的变形矢量图如图4所示，从图4中可以看出：当下沉深度w/D = 0.2时，土体隆起的影响范围约为D；当下沉深度w/D = 0.5时，土体隆起的影响范围约为2D。

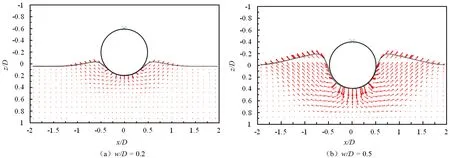
图4　管线下沉过程中土体的变形矢量图

2.3有重正常固结黏土

对于有重黏土，海管下沉过程中，如图4(a)、图4(b)所示的土体隆起将增大管线竖向抗力。对于该情况，采用CEL有限元法对有重正常固结黏土地基中，海管下沉进行计算分析。在计算中，取管线直径D = 0.8 m，土体的不排水抗剪强度随深度线性增加，即su0= sum+ kz，其中：sum=2.3 kPa，k = 3.6 kPa/m，土体有效容重γ′= 6.5 kN/m3。

对于该土质情况，Chatterjee[8]采用RITSS大变形有限元方法进行海管下沉的计算，Tian[15]采用ABAQUS中自带的“mesh-to-mesh solution mapping”方法，并利用Python程序捕捉管线下沉过程中，土体关键节点的位置，从而解决土体大变形的问题，并且管土接触面的最大剪切强度取0.31sum。采用CEL有限元法，考虑管土光滑和粗糙两种接触情况，并与式(1)的理论解进行比较，计算结果如图5所示。从图5中可以看出，CEL有限元法的计算结果与理论解符合程度较好，并且Chatterjee[8]和Tian[15]的计算结果处于管土光滑界面和粗糙界面的结果之间。由此可看出，CEL有限元法模拟管土相互作用问题有很好的适用性，可有效模拟海底管线与土体之间的大变形问题。

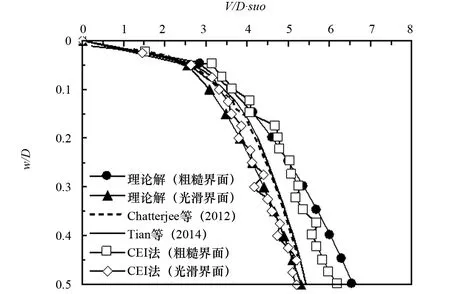
图5　有重正常固结黏土的计算结果

3　结论

准确预测管线安装后的埋深是评价管线侧向稳定性的关键所在。该文采用CEL有限元法，对海底管线自沉的PIP情况进行研究，得到无重均质黏土和有重正常固结黏土中海管下沉阻力和下沉位移之间的关系。研究表明，在无重均质土中CEL有限元法计算得出的归一化竖向力V/Dsu和归一化下沉位移w/D与Merifield的计算结果十分接近；对于有重正常固结黏土，土体容重对土体的隆起将导致下沉阻力增大，CEL有限元法的计算结果与理论解符合程度较好。同时研究也表明，CEL有限元法模拟管土相互作用问题有很好的适用性，可有效模拟海底管线与土体之间的大变形问题。

[1]Merifield R,White D J,Randolph M F.The ultimate undrained resistance of partially embedded pipelines[J]. Géotechnique,2008,58(6): 461-470.

[2]Murff J D, Wagner D A, Randolph M F. Pipe penetration in cohesive soil[J]. Géotechnique, 1989, 39(2): 213-229.

[3]Aubeny C P, Shi H, Murff J D. Collapse load for cylinder embedded in trench in cohesive soil[J]. International Journal of Geomechanics, 2005, 5(4): 320-325.

[4]Randolph M F, White D J. Upper bound yield envelopes for pipelines at shallow embedment in clay[J]. Géotechnique, 2008,58(4): 297-301.

[5]Cathie D N, Jaeck C, Ballard J C, et al.Pipeline geotechnics: State-of-the-art[C]. Proc., Int. Symp. on Frontiers in Offshore Geotechnics: ISFOG 2005.

[6]White D J, Gaudin C, Boylan N, et al. Interpretation of T-bar penetrometer tests at shallow embedment and in very soft soils[J]. Canadian Geotechnical Journal, 2010, 47(2): 218-229.

[7]Wang D, White D J, Randolph M F. Largedeformation finite element analysis of pipe penetration and large-amplitude lateral displacement[J]. Canadian Geotechnical Journal, 2010, 47(8): 842-856.

[8]Chatterjee S, Randolph M F, White D J. The effects of penetration rate and strain softening on the vertical penetration resistance of seabed pipelines[J]. Géotechnique, 2012, 62(7): 573-582.

[9]Merifield R, White D J, Randolph M F. Effect of surface heave on respomse of partially embedded pipelines on clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(6): 819-829.

[10]Randolph M F, White D J. Pipeline embedment in deep water: process and quantitative assessment[C]. In Proceedings of the Offshore Technology Conference, Houston, Tex., 5-8 May 2008. Curran Associates, Inc., Red Hook, N.Y. Paper OTC19128.

[11]Tho K K, Leung C F, Chow Y K, et al. Deep cavity flow mechanism of pipe penetration in clay[J]. Canadian Geotechnical Journal, 2012, 49(1): 59-69.

[12]Shi H, Sun J, Hossain K, et al. Offshore pipeline embedment in cohesive soil - a comparison between existing and CEL solutions[C].In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, OMAE 2011.

[13]Dutta S, Hawlader B, Phillips R. Strain softening and rate effects on soil shear strength in modeling of vertical penetration of offshore pipelines.[C]. In Proceedings of the 9th International Pipeline Conference, IPC 2012.

[14]Randolph M F, Houlsby G T. The limiting pressure on a circular pile loaded laterally in cohesive soil[J]. Géotechnique, 1984, 34(4): 613-623.

[15]Tian Y, Cassidy M J, Randolph M F, et al. A simple implementation of RITSS and its application in large deformation analysis[J]. Computers and Geotechnics, 2014, 56(5): 160-167.

Study of Pipeline Penetration in Clay Based on CEL

HUO Zhi-liang1, YAN Yue2, LI Jia2,3, YAN Shu-wang2,3

(1. Tianjin Municipal Engineering Design & Research Institute, Tianjin 300051, China;2. School of Civil Engineering, Tianjin University, Tianjin 300072, China; 3. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China)

In deep water, pipelines are usually laid directly on the seabed. During the laying process, the pipe typically penetrates into the seabed by a fraction of a diameter. The vertical embedment of pipeline and formation of berm during penetration have a significant effect on the pipeline stability. This study aims to investigate the vertical pipeline penereation at uniform and normal consolidated clay, by carrying out a series of numerical analyses, in which the Coupled Eulerian-Lagrangian method (CEL) was incorporated to enable large deformation simulation. These analyses have been compared with collapse loads calculated using the theory solution. The results show that the CEL method is very suitable for simulating large-deformation pipesoil interaction.

pipeline； self-penetration； theory solution； Coupled Eulerian-Lagrangian method

2015-08-07

国家自然科学基金项目(41272323)。

霍知亮(1987-)，男，博士研究生。

1001-4500(2016)04-0087-06

TU47

A