含双裂纹缺陷海底管道疲劳寿命的分析

余建星， 郭　帅， 吴朝晖， 黄福祥， 李　妍

(1. 天津大学 水利工程仿真与安全国家重点实验室， 天津 300072； 2.高新船舶与深海开发装备协同创新中心， 上海 200240；3. 海洋石油工程股份有限公司，天津 300451)



含双裂纹缺陷海底管道疲劳寿命的分析

余建星1,2， 郭帅1,2， 吴朝晖3， 黄福祥3， 李妍1,2

(1. 天津大学 水利工程仿真与安全国家重点实验室， 天津 300072； 2.高新船舶与深海开发装备协同创新中心， 上海 200240；3. 海洋石油工程股份有限公司，天津 300451)

裂纹缺陷是制约海底油气管道正常运行的关键因素，裂纹会引起管道运行期间的泄漏、断裂，双裂纹共同作用对管道的破坏更为严重。该文研究了含双裂纹缺陷管道的疲劳寿命变化规律，计算了裂纹与管道轴线夹角的变化，双裂纹之间夹角和距离变化对管道疲劳寿命的影响，并对其进行敏感性分析。结果表明，双裂纹之间夹角和距离固定，疲劳寿命随着裂纹与管道轴线夹角的增加而降低，但是变化率逐渐增加；裂纹与管道轴线夹角固定，双裂纹之间夹角和距离变化时，疲劳寿命曲线会出现多个极值点，极小值多出现在夹角为90°时。分析结果可以为海洋工程的实际情况提供参考。

海底管道； 双裂纹； 疲劳寿命； 有限元分析

0　引言

近年来，随着陆地油气资源的日渐枯竭，油气行业逐渐向深海发展。在油气的运输过程中，海底管道的安全稳定运行至关重要。由于海底管道在制造过程中广泛地采用焊接工艺，并且在管道服役过程中，经常会受到落物的撞击，所以管道很容易产生裂纹缺陷。裂纹缺陷引发的管道断裂事故很多，往往造成严重的经济损失及人员安全事故。在工程实际中，裂纹缺陷以多个裂纹相互作用的形式存在，因此，分析多个裂纹之间的相互影响就显得尤为重要。

在含裂纹缺陷管道的分析中，国内外学者已经做了一些工作。国内署恒木[1]分析了含多条轴向裂纹的管道裂纹尖端应力强度因子的变化规律，得出对称裂纹对管道的安全影响最大；秦晓峰[2]研究了厚壁管道均布径向多裂纹的相互作用，得出了随着裂纹数目的增加，最大周向应力会逐渐趋向于一个恒定值等结论。国外Soboyejo和Knott等[3]在实验的基础上分析了多裂纹的相互作用机理；Kachanov等[4]简化了方程中的项，得出了简化的裂纹应力强度因子的计算公式；Qing和Yang[5]在Kachanov方法的基础上做了改进，通过迭代运算得出了较为精确的裂纹应力强度因子的计算公式，并且可以应用到管道多裂纹分析的实际工程中。

但是，国内外学者很少研究双裂纹之间夹角变化所产生的影响。同时，对于双裂纹相互作用对管道疲劳寿命影响的相关研究也较少。该文基于线弹性断裂力学的基本理论，运用ANSYS有限元软件中的Fatigue模块，研究双裂纹缺陷之间的夹角、距离变化对管道疲劳寿命的影响规律。此外，固定双裂纹之间的夹角和距离，改变其中一个裂纹与管道轴线的夹角，分析其对管道疲劳寿命的影响规律。

1　理论基础

1.1裂纹的分类

裂纹的基本类型可分为三类：

Ⅰ型裂纹——张开型裂纹(open mode)；

Ⅱ型裂纹——滑移型裂纹(slide mode)；

Ⅲ型裂纹——撕裂型裂纹(twist mode)。

在实际的工程实践中，还存在三种裂纹混合的型式，裂纹型式如图1所示[6]。

图1　三种裂纹形式

张开型裂纹的受力特点：应力与裂纹面相互垂直，裂纹上下面相互张开；滑移型裂纹的受力特点：剪应力与裂纹面相互平行，并且和裂纹的前端面相互垂直；撕裂型裂纹的受力特点：应力与裂纹的前端面呈现一定的夹角，可以分解为平行于裂纹面和垂直于裂纹面的两部分应力。

具有初始裂纹缺陷海底管道的裂纹型式类似于张开型裂纹，因此着重分析张开型裂纹的特点[7]。

1.2张开型裂纹尖端区域的应力场和位移场

某平板中存在长度为a的裂纹，板的四条边都受到大小为σ的作用力，方向如图2所示。此裂纹形式及受力特点和根据断裂力学的相关理论，推算出该张开型裂纹附近应力场的分布情况，如式(1)所示。

(1)

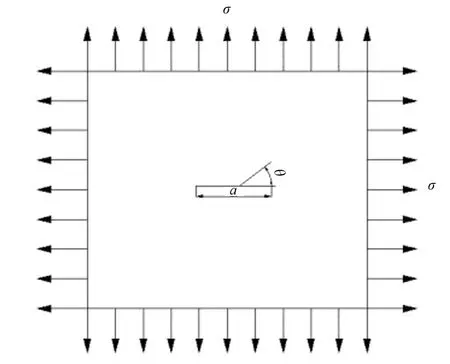
图2　含裂纹薄板示意图

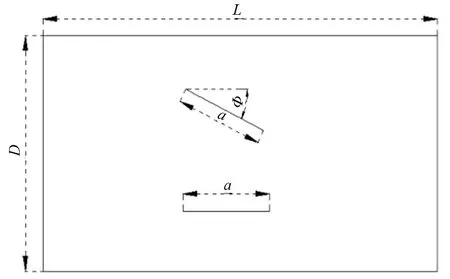
图3　双裂纹间距及夹角示意图

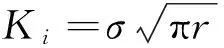
1.3裂纹疲劳扩展寿命的计算

得到应力强度因子之后，根据Paris公式(式2)计算裂纹的扩展速率。

(2)

式中：C和m为材料裂纹扩展性能的基本参数，根据疲劳实验总结得出；△K为应力强度因子的变化值。

将裂纹尺寸a和寿命N向前做差分：

(3)

裂纹扩展一个单位长度△a对应的寿命为：

(4)

对于受到内压力P的管道，在疲劳载荷作用下△K的表达式为：

(5)

根据Paris公式的积分形式即可得到：

(6)

式中：N为管道裂纹扩展到临界尺寸时的循环次数，即管道的疲劳寿命；a0为管道初始裂纹的长度；ac为管道裂纹失稳时的临界尺寸[8]。

2　模型介绍

分析海底油气管道产生双裂纹缺陷的情况下，在海水外压力和管道内油气压力共同作用下的疲劳破坏形式。该文主要研究的是双裂纹之间夹角和距离对管道疲劳寿命的影响。首先分析裂纹和管道轴线夹角变化对具有双裂纹缺陷的管道疲劳寿命的影响，裂纹与管道轴线夹角的示意图如图3所示[8]。

取完整管道作为有限元模拟的模型，根据圣维南原理，计算得L=4 000 mm，模型参数见表1。

表1　模型参数

裂纹参数：长度a=200 mm，深度b=10 mm，设两个裂纹之间的距离为M，裂纹与管道轴线之间的夹角为φ。载荷参数：水深1 000 m时管道所受水体压力P为10 MPa。改变载荷P，模拟P在5 MPa～10 MPa范围内变化时，裂纹疲劳寿命的变化。管道的两端近似成固定端约束，因为管道长度L远大于裂纹半径R，所以产生的误差可以忽略不计。取模型单元为solid45，有限元模型如图4所示。

新生界第四系(Q)：主要分布于研究区的西北部的平原，另外沿河流、沟谷分布，岩性主要为粉沙质粘土、粗砂、砂砾石、细砂层。

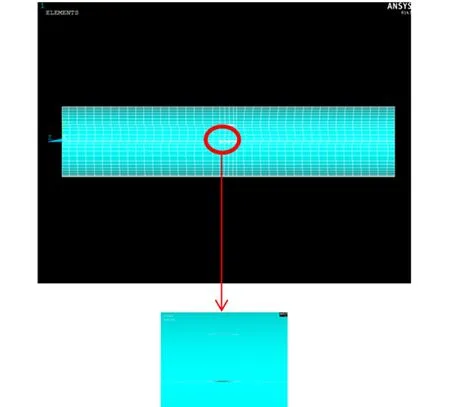
图4　含裂纹缺陷的管道模型图

3　敏感性分析

控制两个裂纹的长度和深度不变，裂纹间距M=200 mm，改变其中一个裂纹与管道轴线的夹角φ=0°，15°，30°，45°，60°，75°，90°，采用ANSYS中的Fatigue模块，计算管道疲劳破坏时的循环次数，并研究其变化规律，计算结果如图5所示。

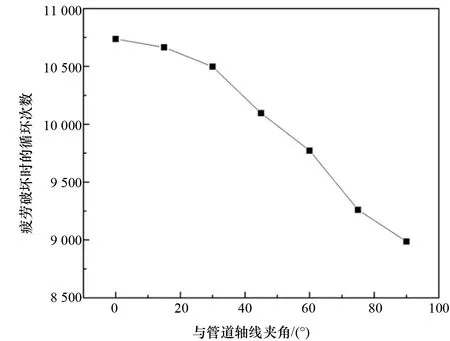
图5　管道疲劳寿命随裂纹间夹角变化的趋势

疲劳破坏时循环次数的变化规律和疲劳寿命的变化规律相似，由图5可以看出：裂纹间距M=200 mm，含双裂纹缺陷管道的疲劳寿命随裂纹与管道轴线夹角的变化明显。φ从0°～90°的变化过程中，管道的疲劳寿命逐渐降低。当裂纹与管道轴线的夹角较小时，疲劳寿命随着角度的降低变化缓慢，随着角度的增加，降低的速率逐渐增加。即在相同夹角变化值(△φ)的情况下，疲劳寿命减少的速度越来越快，说明△φ/φ越小，疲劳寿命变化的越快。

4　模型介绍

在得到裂纹与管道轴线夹角变化对具有双裂纹缺陷管道的疲劳寿命的影响之后，继续研究双裂纹之间夹角和距离对含双裂纹缺陷管道疲劳寿命变化规律的影响。双裂纹之间的夹角和距离的相对情况如图6所示，M表示双裂纹左端边缘线之间的距离，θ表示双裂纹之间的夹角。

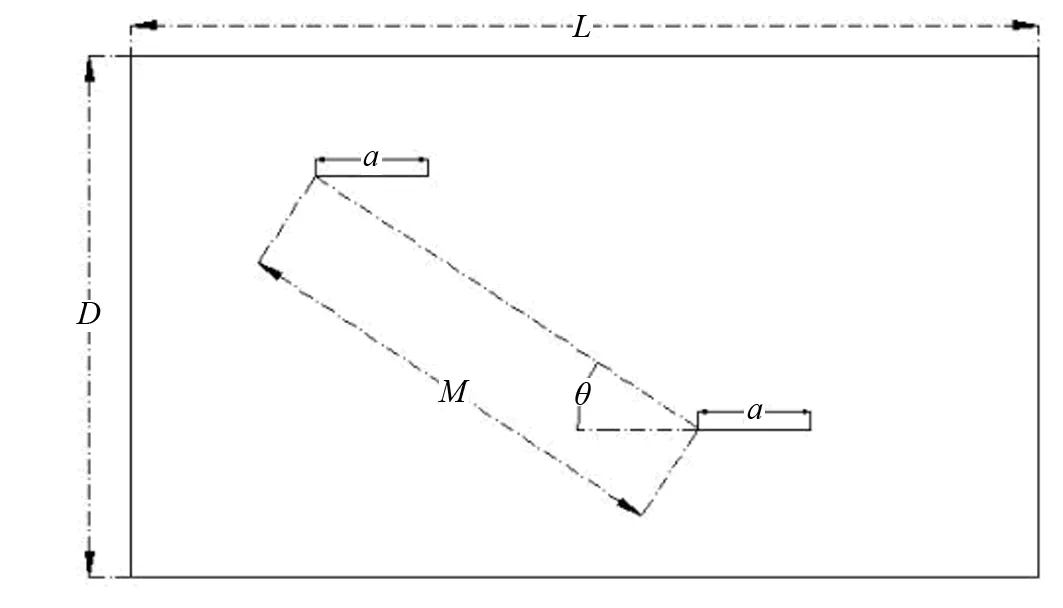
图6　双裂纹间距及夹角示意图

为了减少双裂纹之间夹角和距离变化时，裂纹的形状参数对有限元模拟结果的影响，特模拟锥形尖锐物体碰撞管道后留下的缺陷，这样可以减少裂纹夹角变化时裂纹形状对模拟结果的影响。管道的模型参数和第2节中模型的参数相同，两端仍采用固支约束。模拟载荷P在5 MPa～10 MPa范围内管道疲劳寿命的变化规律，有限元模型图如图7所示。

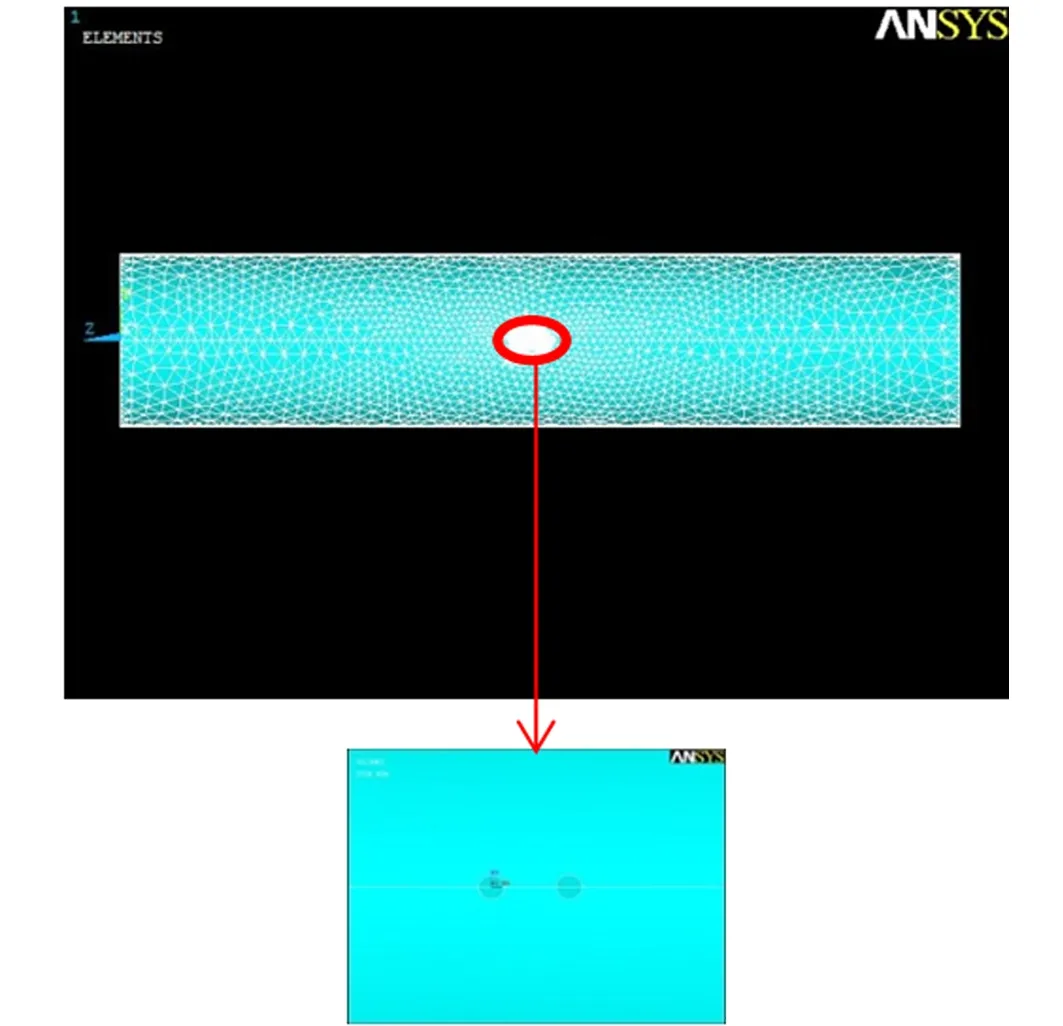
图7　含裂纹缺陷的管道模型图

5　敏感性分析

控制两个裂纹的形状、深度不变，双裂纹之间的距离M=50 mm，所受载荷区间为5 MPa～10 MPa，改变裂纹之间的夹角θ=0°，15°，30°，45°，60°，75°，90°，做7组不同的数值模拟，采用ANSYS中的Fatigue模块，计算管道疲劳破坏时的循环次数，并研究其变化规律，计算结果如图8所示。

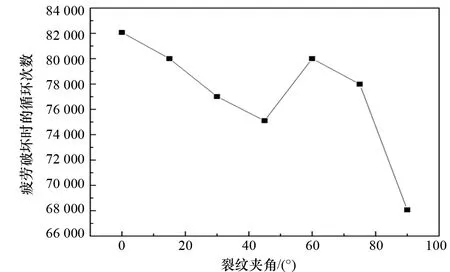
图8　管道疲劳寿命随裂纹间夹角变化的趋势

疲劳破坏时循环次数的变化规律和疲劳寿命的变化规律相似，由图8可以看出：裂纹间距M=50 mm时，含双裂纹缺陷管道的疲劳寿命随裂纹夹角的变化明显。从0°～45°时，管道的疲劳寿命逐渐减小，θ=45°时达到极小值。在θ=60°时疲劳寿命达到极大值，之后逐渐降低，最后θ=90°时达到最小值。因此在裂纹间距M=50 mm的情况下，θ=45°和θ=90°时最容易发生疲劳破坏。含缺陷管道裂纹的应力最大值点应该出现在裂纹的尖端处，由此可知双裂纹的夹角对裂纹尖端的应力最大值有比较明显的影响。

对照上组数值模拟，其他模拟的条件都相同，只改变双裂纹之间的距离M=100 mm，150 mm，200 mm，250 mm。针对不同的裂纹间距值，分别做θ=0°，15°，30°，45°，60°，75°，90°七组数值模拟，得到M=100 mm，150 mm，200 mm，250 mm时管道疲劳破坏时循环次数的规律图，将五组规律图整合到一张图中，如图9所示。

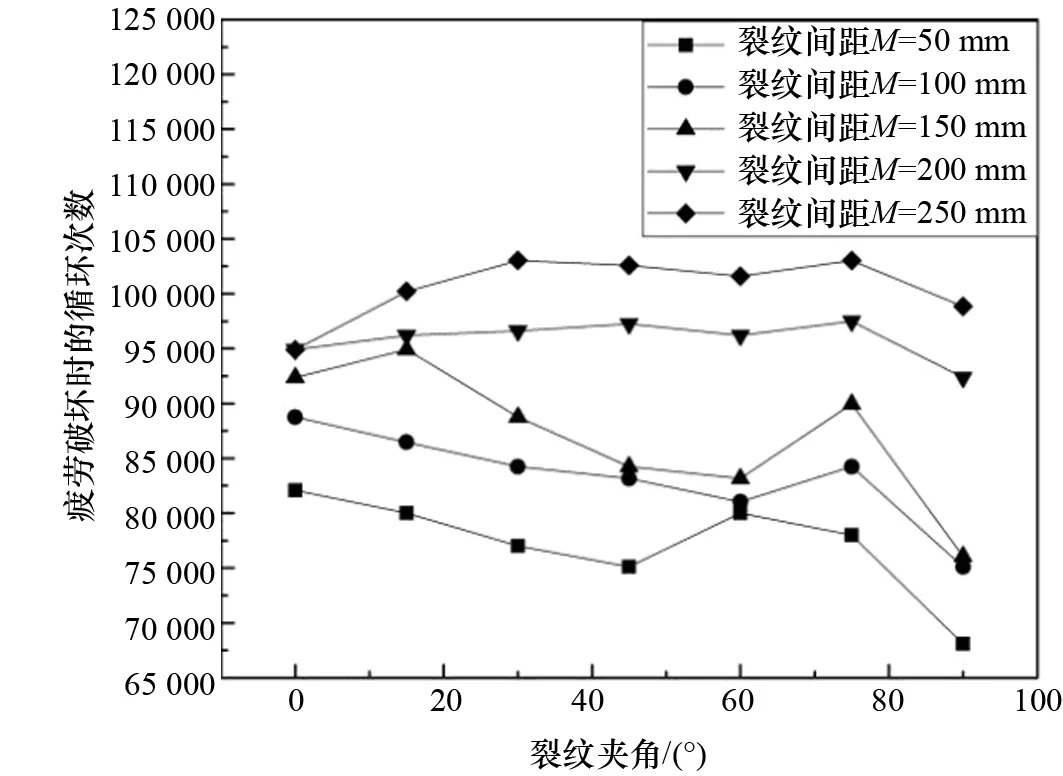
图9　管道疲劳寿命随裂纹间夹角变化的趋势

疲劳破坏时循环次数的变化规律和疲劳寿命的变化规律相似，通过图9可以看出疲劳寿命的变化规律为：

(1) 波动程度。裂纹间距M=50 mm，100 mm，150 mm时，曲线的波动程度比较大，变化过程中都有比较突出的极值点；M=200 mm，250 mm时，曲线的波动程度比较小，变化比较平缓。当裂纹间距增大到一定程度时，裂纹夹角变化对疲劳寿命的影响变小。

(2) 极值的分布。M=50 mm时，极大值出现在θ=0°，60°处，极小值出现在θ=45°，90°处；M=100 mm时，极大值出现在θ=0°，75°处，极小值出现在θ=60°，90°处；M=150 mm时，极大值出现在θ=15°，75°处，极小值出现在θ=0°，60°，90°处；M=200 mm时，极大值出现在θ=45°，75°处，极小值出现在θ=0°，60°，90°处；M=250 mm时，极大值出现在θ=30°，75°处，极小值出现在θ=0°，60°，90°处。从安全的角度考虑，应该关注疲劳寿命较小的点，同时，在裂纹间距较小时，疲劳寿命的最小值点多出现在θ=90°时，当裂纹间距M=250 mm时，最小值出现在θ=0°。

(3) 裂纹间距的影响。在裂纹夹角相同的情况下，裂纹间距越小，管道的疲劳寿命越小，管道发生破坏的可能性就越大。

含缺陷管道裂纹的应力最大值点应该出现在裂纹的尖端处，即疲劳寿命值最小的点，由此可得双裂纹的距离和夹角对管道的疲劳寿命有比较明显的影响。

6　结论

该文基于断裂力学和线弹性力学的相关理论，通过ANSYS有限元软件模拟含双裂纹缺陷管道的疲劳寿命变化规律，分析了双裂纹之间的距离、夹角以及裂纹与管道轴线夹角对管道疲劳寿命的影响，得出了以下结论：

(1) 改变裂纹与管道轴线夹角对含双裂纹缺陷管道的疲劳寿命影响明显，在夹角φ从0°～90°的变化过程中，管道的疲劳寿命逐渐降低，并且角度越大，降低的速率越快。

(2)改变双裂纹之间的距离和夹角。在裂纹间距M=50 mm，100 mm，150 mm，200 mm，250 mm五种情况下，管道疲劳寿命曲线的波动程度随着M的增大逐渐减小。

(3)疲劳寿命的极小值点。裂纹间距M=50 mm，100 mm，150 mm，200 mm，250 mm五种情况下，裂纹间距比较小的时候，疲劳寿命的最小值点多出现在θ=90°时，裂纹间距较大时，疲劳寿命的最小值点出现在θ=0°时。

(4)在双裂纹夹角θ相同的情况下，管道的疲劳寿命随着裂纹间距的减小而逐渐降低，管道发生疲劳破坏的可能性越大。

[1]署恒木. 厚壁筒径向裂纹最危险分布[J],石油化工设备,2000,29(5)：12-14..

[2]秦晓峰. 厚壁管道均布径向多裂纹相互作用的有限元研究[D].沈阳：东北大学,2011.

[3]Soboyejo W O,Knott J F. Fatigue crack propagation of coplanar semi-elliptical cracks in pure bending [J]. Engineering Fracture Mechanics, 1990,37(5):323-340.

[4]Mark K. Elastic solids with many cracks: A simple method of analysis [J]. International Journal of Solids and Structures, 1987,23(1):23-43.

[5]Qing H,Yang W. Characterization of strongly interacted multiple cracks in an infinite plate [J].Theoretical and Applied Fracture Mechanics, 2006,46(6):209-216.

[6]解德. 断裂力学中的数值计算方法及工程应用[M]. 北京：科学出版社，2009.

[7]金伟良，付勇，赵冬岩，等. 具有裂纹损伤的海底管道断裂及疲劳评估[J]. 海洋工程，2005，23(3)：7-16.

[8]卞雪航,吴海欣,余杨,等. 深水海底管道屈曲传播试验设计[J]. 海洋技术,2011,30(4):93-95+131.

[9]周义清,王志华,马宏伟. 超声纵向导波进行管道裂纹检测的数值模拟[J]. 中北大学学报(自然科学版),2006,28(3):258-262.

[10]何雪,秦晓峰,谢里阳,等. 管道轴向双裂纹夹角对尖端应力强度因子的影响[J]. 东北大学学报(自然科学版),2011,32(11):1623-1626.

[11]王海兰，马廷霞，徐洪敏，等. 输油悬空管道洪水冲刷作用下的安全评价[J]. 石油机械，2015，43(1)：112-118.

Analysis of Fatigue Life for Subsea Pipelines with Double Cracks

YU Jian-xing1,2, GUO Shuai1,2, WU Zhao-hui3, HUANG Fu-xiang3, LI Yan1,2

(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University,Tianjin 300072, China； 2. Collaborative Innovation Center for Advanced Ship and Deep-sea Exploration, Shanghai 200240, China； 3. Offshore Oil Engineering Co., Ltd, Tianjin 300451, China)

Crack defects are the key to determine the smooth operation of subsea oil-gas pipelines. Crack defects would greatly increase the probability of pipelines′ leakage and fracture, and double cracks would cause severer damage to pipelines. Aiming at fatigue life′s variation of pipelines with crack defects, calculation was adopted to analyse the sensitivity of included angle between cracks and pipeline′s axis, and sensitivity of included angle and distance between cracks. In conclusion, when angle and distance between cracks are determined, fatigue life of pipeline decreases at an increasing rate due to increase of angle between cracks and pipeline′s axis. Besides, when angle between cracks and pipeline′s axis is determined but angle and distance between cracks are not, there are 2 or 3 extreme value of the fatigue life, mostly located at θ=90°. The conclusion may provide reference for ocean engineering practices.

subsea pipeline; double cracks; fatigue life; finite element analysis

2016-01-26

国家重点基础研究发展计划(973计划)资助项目(2014CB046804)，国家自然科学基金资助项目(51239008)，国家自然科学基金资助项目(51379145)。

余建星(1958-)，男，教授。

1001-4500(2016)04-0066-07

P75

A