引入运动 妙成编题*——对一道向量习题的反思

●张　健　唐恒钧

(浙江师范大学教师教育学院　浙江金华　321004)



引入运动妙成编题*
——对一道向量习题的反思

●张健唐恒钧

(浙江师范大学教师教育学院浙江金华321004)

文章采用“运动”的观点对一道向量习题进行了反思，在此基础上编制了一些数学习题，并产生了对编题的思考.

向量习题；反思；编题

著名数学教育家波利亚非常重视解决问题之后的反思，他在《怎样解题》中指出:通过回顾完整的答案，重新斟酌、审查结果及导致结果的途径，他们能够巩固知识，并培养他们的解题能力[1].对问题进行反思可以加深对于问题的理解，发展解决问题的能力，因而“数学解题及其教学应该注重通过‘回顾与反思’来提出新的问题，从典型的问题出发去变式、去引申、去发现，这样常常可以得到一些意想不到的结论”[2].最近，笔者在学习过程中接触到一道具有几何背景的向量习题，反思这道习题的过程引发了笔者对于编制数学习题的一些思考.

1　习题的呈现

在文献[3]和文献[4]中，有这样一道习题：

图1

图2

文献[3]和文献[4]都对该题进行了解答和证明.为了下文叙述方便，笔者把该题的解答过程呈现如下：

于是

另一方面，点M，G，N共线，因此存在p，q满足p+q=1，使得

解得

于是

即

2　对习题的反思

下面笔者从题目的条件、结论和证明过程2个角度反思例1中的习题.

2.1对条件、结论的反思

2.2对证明过程的反思

例1的问题情境是静态的，以上的反思让我们产生了采用“运动”的观点来对题目进行改造的想法.在运动的过程中，例1就成为了一个特殊的状态和一个特例，问题也从特殊情形变成了一般情形，笔者从中编制出许多数学习题.

3　编题的产生

3.1直线MN绕重心G转动

图3

图4

在直线MN转动过程中，直线MN与AB，AC不一定总有交点，因此可以考虑参数的取值范围，编题如下：

图5

图6

3.2点G沿中线AD所在直线运动

文献[4]对例1中重心G的位置进行了推广，将点G改为中线AD上的其他点[4]，但点G的运动范围只限于三角形内部，因而仍然有局限性.笔者对此结果进一步推广并重新叙述如下：

证明点D为BC的中点，从而

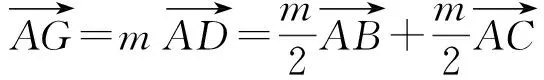
另一方面，点M，G，N共线，于是存在p，q满足p+q=1，使得

解得

于是

即

定理2中并没有限制m的范围，只要保证点M，G，N共线，结论都可以成立.因此，点G不一定要限制在三角形内部,可以将点G沿AD所在直线运动，并且还可以反向延长BA，CA，如图7～9，结论仍然成立，这些图形都可以作为编题的材料.

图7

图8

图9

图10

图11

3.3点D沿直线BC运动

上面的讨论说明了在图形之中引入了“运动”之后的效果，我们站在更广阔的视野看待原有问题，也编出了一些题目.因此，可以让图形进一步“运动”起来，将中点D的位置视作运动过程中的特殊状态，让点D沿BC运动.

另一方面，点M，G，N共线，因此存在p，q满足p+q=1，使得

解得

于是

即

定理3给出了这个图形在运动之中的一般规律，本质上也将例1的情形推广到了一般情形.笔者惊奇地发现，将“运动”引入例1后，经过一步步地演化，问题已经从特殊的情形变成了一般的情形，这正是“运动”带来的奇妙效果.这个图形总共有3个运动的要素：直线MN绕点G转动、点G沿直线AD运动、点D沿直线BC运动，它们互相结合可以演变出许多不同的图形，从中可以编制出许多题目.比如，可以赋予参数具体的数值，选取一个运动状态来进行如下的编题：

证明由定理3，可知

从而

由题意λ1>0,λ2>0，根据柯西不等式知

即

4　对编题的思考

数学习题的一大价值在于帮助学生加深对知识的理解，在解决问题的过程中发展学生的问题解决能力，促进数学思维的发展.而传统的编题过程往往只停留于经验，注重变式而较少关注题目的价值，对题目缺少系统的组织.这导致了数学习题十分冗杂，成为杂乱无章的“题海”，对学生的学习也是不利的.编题者首先需要深入了解问题的结构，这样才能编出促进学生思维发展的有价值的题目.在反思旧问题的过程中编题，不仅可以深入了解问题的结构，还可以挖掘出隐藏在问题背后更多的素材，这是编题的重要来源.围绕一种观点对问题进行反思从而编题(比如本文采用的“运动”观点)，不仅推广了原有问题并编制出了新的习题，编制出的题目也成为一个相互联系的“题族”.

[1]波利亚．怎样解题：数学教学法的新面貌[M]．涂泓，冯承天，译．上海：上海科技教育出版社，2002．

[2]徐彦辉.数学解题后的“回顾与反思”与数学问题的提出——探索一种通过“回顾与反思”来提出数学问题的模式与方法[J].数学教育学报，2015(1)：9-12.

[3]江保兵.平面向量的共线定理及其推论[J].中学数学研究，2014(2)：27-28.

[4]苏庆飞.平面向量中三点共线定理的应用与推广[J].数理化学习:高三，2013(4)：19-20.

�2016-05-04；

2016-06-27

张健(1993-)，男，浙江温州人，硕士研究生.研究方向：数学教育.

O123.1

A

1003-6407(2016)10-22-04