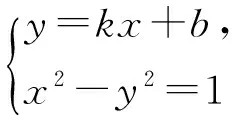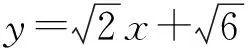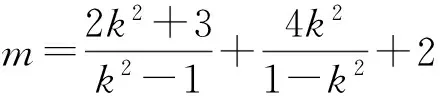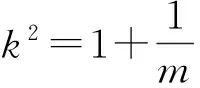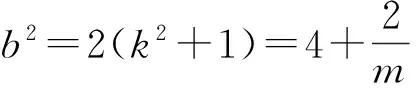善变陈题 触类旁通 精于设计*
2016-10-31何伟军
●何伟军
(渭源县第一中学 甘肃渭源 748200)
善变陈题触类旁通精于设计*
●何伟军
(渭源县第一中学甘肃渭源748200)
文章以一道陈题为变式“生长点”,对其进行创新设计,演绎出16个变式题,涉及常见圆锥曲线的热点(考点)问题.旨在夯实基础,提升解题能力,培养学生灵活多变的思维品质和创新精神,这也是数学高考复习实施高效教学的重要途径之一.
陈题;变式;探求问题
数学高考复习时间紧、量大面宽是众所周知的.要搞好圆锥曲线复习,必须在精选、精讲、精练题上狠下功夫,必须将问题适度拓展、改造、组合、串并联,形成圆锥曲线高考热点问题组,使知识的获得、能力的形成放植于有效的变式训练中,只有变式的“教与学”,方可走出“题海”,达到回头是“岸”之境界,真正减轻学生负担,培养学生灵活多变的思维品质和创新精神.笔者试图以一道陈题为变式“生长点”,演绎出精彩高效的圆锥曲线热点问题.
原题讨论直线l:y=kx+1与双曲线C:x2-y2=1公共点的个数.
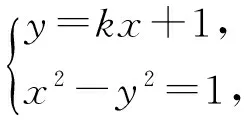
(1)
当1-k2=0,即k=±1时,x=∓1.当1-k2≠0,即k≠±1时,
Δ=4k2+8(1-k2)=8-4k2,
由Δ>0得
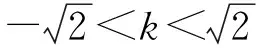
由Δ=0得
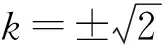
由Δ<0得
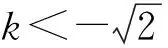
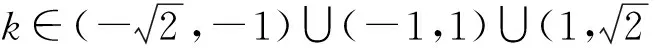
这是一道常规题.如果我们创设问题的新情境,陈题新编,纵横拓展,迁移组合,将会囊括圆锥曲线问题中“参数的取值范围、定值、对称、轨迹、定点”等高考热点问题,做到举一反三,助推能力提升.
1 探求参数的取值范围
变式1若直线l与双曲线C有2个不同的交点A,B,求实数k的取值范围.
变式2若直线l与双曲线C的右支交于2个不同的点A,B,求实数k的取值范围.
变式3若直线l与双曲线C的左支交于2个不同的点A,B,求实数k的取值范围.
变式4若直线l与双曲线C的左、右2支交于不同的点A,B,求实数k的取值范围.
评注此类题应数形结合,根据直线l与双曲线C交于1支(或2支)找到其充要条件,列出不等式组是正确求解取值范围的关键.
变式5若直线l′垂直平分变式1中的弦AB,求l′在y轴上的截距m的取值范围.
思考:若直线l′垂直平分变式2、变式3、变式4中的弦AB,求l′在y轴上的截距m的取值范围.其结果又有什么不同?
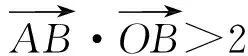
评注在变式5、变式6中含有2个参数,m的变化是由k引起的,且m是关于k的函数,我们在2个参变量之间建立函数m=f(k)是关键,问题转化为求此函数的值域.
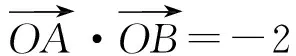
2 探求定值问题
变式8若直线l与双曲线C有2个不同的交点A,B,且A,B都在以M(0,-3)为圆心的圆上,求k的值.
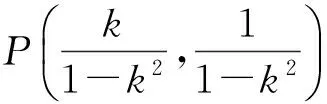
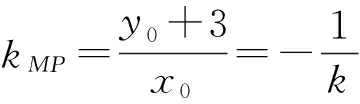
得直线MP的方程为
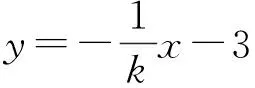
即
x+ky+3k=0,
从而
x0+ky0+3k=0,
得
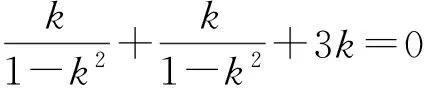
即
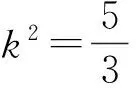
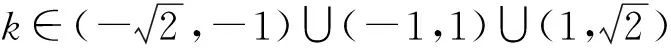

变式9是否存在实数k,使得以直线AB为直径的圆经过双曲线C的右焦点F2.若存在,求出k的值;若不存在,请说明理由.
解由题意知F2A⊥F2B,设A(x1,y1),B(x2,y2),右焦点为F2(c,0),则
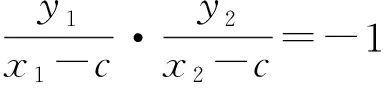
即
x1x2+y1y2-c(x1+x2)+c2=0.
又
y1y2=k2x1x2+k(x1+x2)+1=1,
得
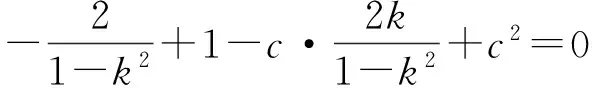
即
(1+c2)k2+2ck+1-c2=0.
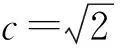
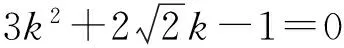
解得

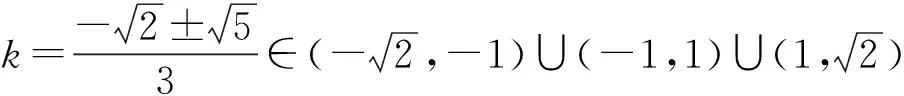
评注陈题条件中加入“A,B在圆上”后,问题分别以求定值和探求存在型的方式呈现,给人以“似曾相识”的感觉,顿生解决问题的欲望与激情.解决这类问题能增强学生的代数运算能力和识图能力.
3 探求对称问题
变式10若直线l与双曲线C有2个不同的交点A,B,是否存在这样的实数k,使得A,B这2个点关于直线l′:y=ax(其中a≠0)对称?若存在,求出实数k;若不存在,说明理由.
解假设存在满足条件的k,使得点A,B关于直线l′对称,并设A(x1,kx1+1)和B(x2,kx2+1)关于直线l′对称,则
整理得
(k-a)(x1+x2)+2=0.
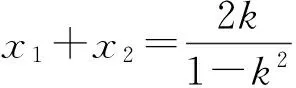
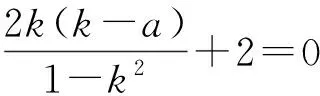
即
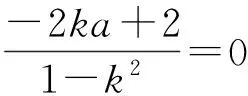
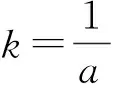
评注对称问题中“嵌套”存在型问题,使陈题面目为之一新,既考查了AB⊥l′和AB的中点在l′上这2个关系,又考查了学生综合运用数学知识进行推理运算的能力.求解圆锥曲线的对称问题,常见的问题是找不出所设变量之间的关系导致解答寸步难行.
4 探求动点的轨迹方程问题
变式11若直线l与双曲线C有2个不同的交点A,B,求弦AB中点的轨迹方程.
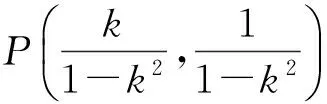
问题探究如何确保参数方程与普通方程等价呢?
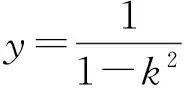
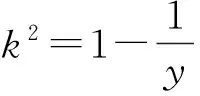
从而
即
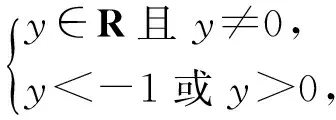
解得
y<-1或y>0.
又k2≥0,得
y<0或y≥1.
综上可得
y<-1或y≥1,
因此弦AB中点的轨迹方程为
x2-y2+y=0(其中y<-1或y≥1).
问题探究题设的限制条件如何寻找?
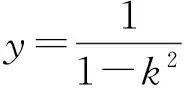
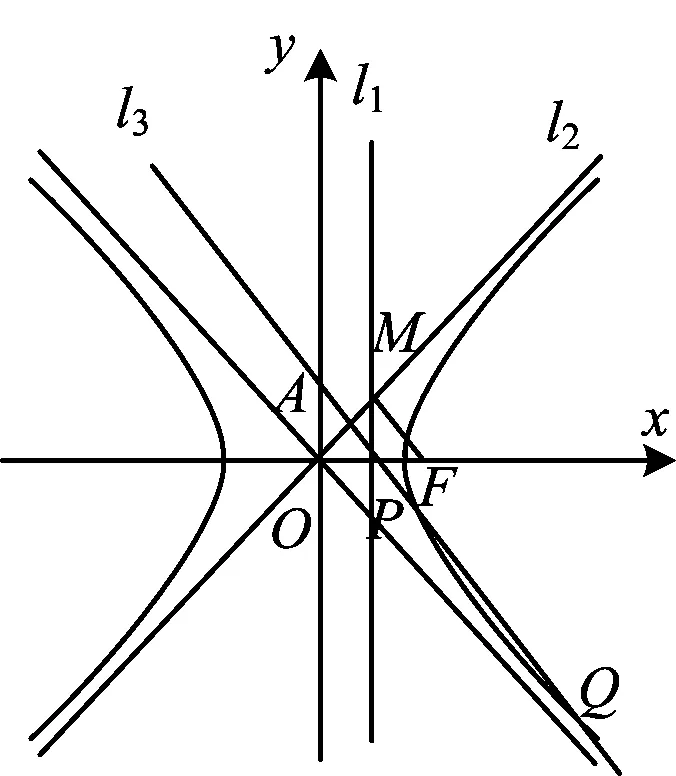
0≤k2<1或1 从而 0<1-k2≤1或-1<1-k2<0, 即 y<-1或y≥1, 因此,弦AB中点的轨迹方程为 x2-y2+y=0(其中y<-1或y≥1). 评注选择以斜率为参变量,或用“点差法”找到斜率与弦中点之间的关系后,先求出参数方程,再化为普通方程,即点P的轨迹方程为 x2-y2+2y=0(其中y<-2或y≥2). 特别注意参数方程与普通方程的等价性是易错点,也是难点和关键点. 解设Q(x0,0),则 即 而 y1y2=k2x1x2+k(x1+x2)+1=1, 代入上式可得 解得 评注以陈题和2006年山东省数学高考试题为雏形设计定点问题,也是高考的热点之一.先求出满足条件的直线l,然后再利用直线过定点知识加以解决.与平面向量的结合,既体现了几何与向量的交汇,也体现了数形结合的巧妙应用. 整理得 28k4-55k2+25=0, 解得 (x1,y1)+(x2,y2)=(λx0,λy0), λ2=16, 即 λ=±4. 因此,△ABP的面积为 变式15若直线l:y=kx+b与双曲线C:x2-y2=1的左支交于2个点A,B,直线l与以F1F2为直径的圆相切. x2+y2=2. 由于直线l与⊙O相切,从而 即 b2=2(k2+1)(其中k≠±1). (2) (k2-1)x2+2kbx+b2+1=0, (1+k2)x1x2+kb(x1+x2)+b2= 化简整理,得 (3) 联立式(2)和式(3)得 2k2+3-4k2+k2-1=0, 解得 此时 Δ=4k2b2-4(k2-1)(b2+1)>0, 得 k2≠1, 从而 由k,b同号知,直线l的方程为 2)类似于第1)小题可得 即 从而 根据弦长公式 因为点O到直线l的距离为 而2≤m≤4,所以当m=2时,△AOB的面积最小,其值为 当m=4时,△AOB的面积最大,其值为 评注设置多个变量,适当改编条件,用待定系数法逆向求解斜率和截距,使思维量加大,思维的难度增大.但方程思想作基础,先利用“减元”思想列出△AOB面积是m的函数,再利用二次函数在给定的区间上求最值的方法可解决. 图1 即 a=b. 即 又b2=1,即a2=1,得双曲线C的方程为 x2-y2=1. 3)解由题意可得0<λ<1. 证明设l3:y=kx+1,点P(x1,y1),Q(x2,y2),则由l3与双曲线C右支交于不同的2个点P,Q及变式2得 (x1,y1-1)=λ(x2,y2-1), 得 x1=λx2, 从而 于是 0 从而 即 λ2-2λ+1>0, 因此λ的取值范围是(0,1). 评注逆向设计、用向量的坐标法证明问题是亮点之一;交换条件与结论后探究x2-y2=1为亮点之二;最后以参数的范围求解、几何问题代数化结尾. 精选典例,抓住“娇”题不放,创新变式.若能从“变”的表象中发现“不变”的本质,从“不变”的假象中掘出“变”的内涵,则能促使学生尽快领悟数学思想方法,形成高超数学能力.变式教学不仅是跳出题海、减轻学生负担、以少胜多、实施高效教学的最佳选择,而且也是全方位提升学生分析问题和解决问题能力的明智之举. �2016-06-21; 2016-07-22 何伟军(1962-),男,甘肃定西人,中学高级教师.研究方向:数学教育. O123.1 A 1003-6407(2016)10-17-05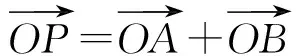
5 探求定点问题
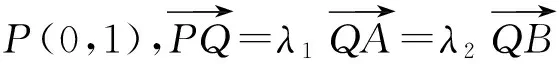

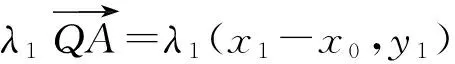
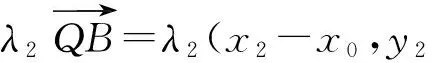
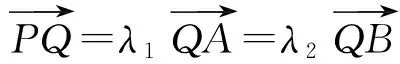
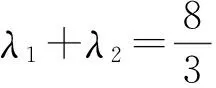
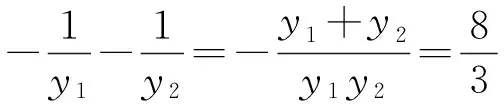
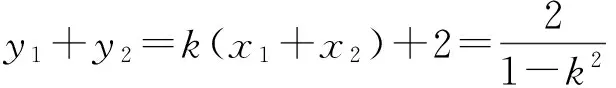
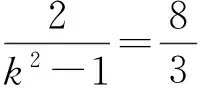
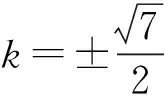
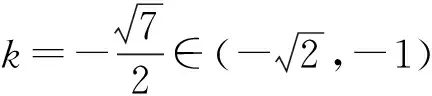
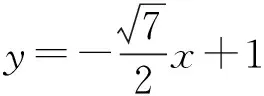
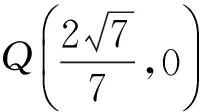
6 探求面积问题
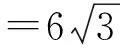
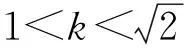
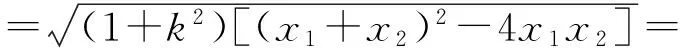
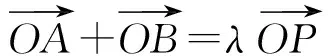
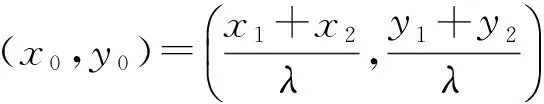
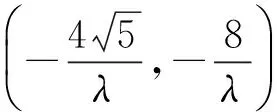
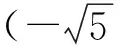
7 多元设置,综合压轴