三角函数型不等式恒成立问题的7种策略*

●魏正清

(临泽县第一中学　甘肃临泽　734200)



三角函数型不等式恒成立问题的7种策略*

●魏正清

(临泽县第一中学甘肃临泽734200)

含参三角函数型不等式恒成立的问题，是竞赛的热点，也是难点，解法多变，无规律可循.文章给出可分离参数的三角函数型不等式恒成立求参数范围的7种策略.

三角函数型不等式;求参数范围;策略

含参不等式恒成立问题，可把不等式、函数、三角、几何等内容有机地结合起来，以覆盖知识点多、综合性强、解法灵活等特点而倍受关注.尤其是三角函数型不等式恒成立求参数范围的问题，一直是竞赛命题的热点，在近几年的高考中，也日益受到命题者的青睐.如何破解参数可分离的三角函数型不等式恒成立求参数范围的问题，值得关注.笔者给出破解此类问题的7种策略，以期抛砖引玉.

1　利用柯西不等式

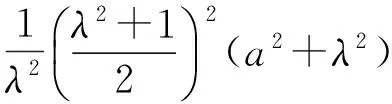
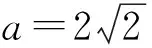
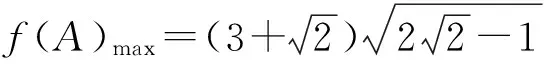
评注对于三角函数型多变元不等式恒成立求参数范围的问题，分离参数后，求函数最值时，若能先固定一元，则可活化思维，柳暗花明.减元是求函数最值问题最重要的思路，而巧妙地引入参数、利用柯西不等式是求解多元最值问题最有效的方法之一.

2　利用几何意义

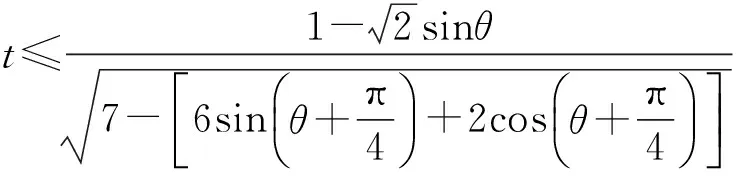
评注对于形式繁琐、结构特征明显的不等式恒成立问题，若能紧扣式子的几何特征，巧妙地利用其几何意义，数形结合，则可迅速找到解题的突破口.

3　构造和函数

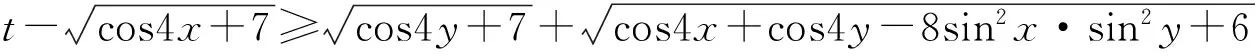
分析依题意，要使

恒成立，可令cos2x=a，cos2y=b，则0≤a≤1,0≤b≤1，于是

由0≤a≤1,0≤b≤1知

评注对于变元易分离的多变元不等式恒成立问题，可将函数的最值转化为几个函数的最值之和处理.

4　构造递推式

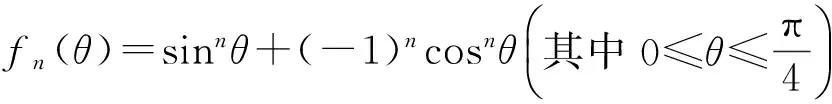
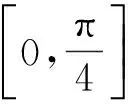
2f2k(θ)-f2k-2(θ)=(cos2k-2θ-sin2k-2θ)(cos2θ-sin2θ)≥0,

得

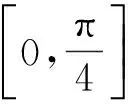
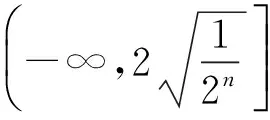
评注对于具有数列特征的多变元不等式恒成立问题，求函数的最值时，可利用数列思想构建递推不等式，使问题巧妙解决.

5　换元法

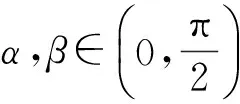
x=sin2αcos2β，y=sin2αsin2β，z=cos2α,

则

x+y+z=1.

评注对于形式复杂，但都是sinx与cosx的偶次方的三角函数型不等式恒成立问题，若能巧妙地利用球坐标变换，则可迅速简化问题，让人耳目一新.

6　先猜后证

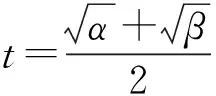
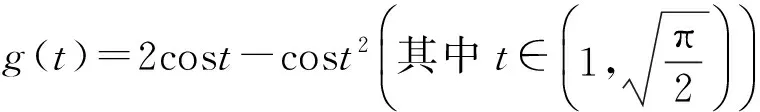
于是f<1.

综上所述，f<1，实数t的取值范围是(-∞,1].

评注对于结构复杂、分离参数后不易求最值的多元函数，若能先猜出其最值，再加以证明，则可迅速找到解题的突破口.

7　构造单调函数

分析依题意可得

即

f(cosθ)≤f(sinθ),

评注对于结构特征明显、但又不易化简的三角不等式恒成立问题，若能根据其特征巧妙地构造单调函数，利用其单调性，定有意想不到的收获.

�2016-04-19；

2016-05-20

甘肃省十二五规划课堂(GS[2015]GHB1415)

魏正清(1968-)，男，甘肃张掖人，中学高级教师.研究方向：数学教育.

O122.3

A

1003-6407(2016)10-09-04