习题变式教学在思维对话中进行*
2016-10-31郭建华
●郭建华
(南京市第二十九中学 江苏南京 210036)
●于 健
(金陵中学 江苏南京 210005)
习题变式教学在思维对话中进行*
●郭建华
(南京市第二十九中学江苏南京210036)
●于健
(金陵中学江苏南京210005)
通过课本习题的辐射功能,让课本习题充分起到“巩固基础知识、提炼解题方法、发展思维的载体”的作用.通过思维对话的形式,调动学生的主观能动性,激活其原有认知结构中适当的观念和感性经验,调动学生有意义的学习心向,让变式教学更具有价值和意义.
习题变式;对话交流;发展思维
著名数学教育家波利亚曾形象地指出:“好问题同某些蘑菇有些相像,它们都成堆地生长,找到一个以后,你应当在周围找一找,很可能附近就有好几个.”数学课堂教学中的变式教学,就如同波利亚所说的蘑菇.所谓“变式”,就是指教师有目的、有计划地对命题进行合理地转化,即教师可不断更换命题中的非本质特征,变换问题中的条件或结论,转换问题的内容和形式,配置实际应用的各种环境等,但应保留问题中的本质因素,从而使学生掌握数学对象的本质属性.通过变式教学的探究,在思维对话中充分调动学生学习数学的主观能动性,引导学生主动参与探究,从而达到发展学生数学思维的目的.
课本中的习题不仅仅是巩固基础知识、提炼解题方法、发展思维能力的载体,如果我们对它们进行认真研究,那么这些习题还可作为探究教学的重要资源.笔者尝试从课本习题入手,并结合数学探究教学作了初步探究.
下面以苏教版高中数学必修1第3章复习题第14题(第111页)教学为例.
题目[1]若关于x的方程3tx2+(3-7t)x+4=0的2个实根α,β满足0<α<1<β<2,求实数t的取值范围.
1 分析解法,深化理解
生1:先求出方程3tx2+(3-7t)x+4=0的2个实根:
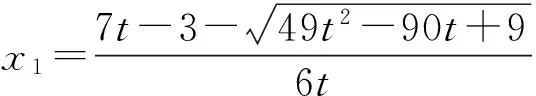
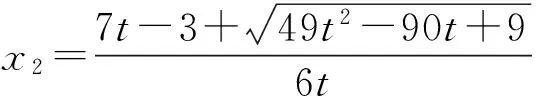
再结合2个实根α,β满足0<α<1<β<2,求出实数t的取值范围.
师:如何判断2个实根x1,x2的大小呢?
生1:令f(x)=3tx2+(3-7t)x+4,由f(0)=4>0,得t>0,从而x1 解得 师:有没有其他解法? 生2:利用二次方程区间根的分布,结合二次函数图像求解,设f(x)=3tx2+(3-7t)x+4,因为f(0)=4>0,且方程3tx2+(3-7t)x+4=0的2个实根分别在区间(0,1)和(1,2)上,得 从而 评注此题重在研究一元二次函数、一元二次方程与一元二次不等式3个二次之间的关系,属于中等难度,考查一元二次方程根的分布问题.解法2明显优于解法1,解法1完全从代数的角度思考问题,但不等式的求解较为复杂.解法2借助于数形结合的思想,利用二次方程区间根的分布求解,此解法不但摆脱了思维定式的影响,而且达到了优化思维和简化运算的目的. 在习题教学过程中,教师要善于捕捉一些典型习题的求解信息,以及关注习题的变式教学和探索,沟通数学知识与技能、数学思想与方法的纵横联系.这样不仅能极大地激发学生学习数学的兴趣和热情,而且更有利于学生分析问题、解决问题能力的提升. 2.1改变条件,激活探究思维 变式1设函数f(x)=3tx2+(3-7t)x+4(其中t<0)的2个零点x1,x2,且在区间(x1,x2)上恰有3个正整数,求实数t的取值范围. 生3:其实该题考查的还是3个二次之间的关系,可以利用二次方程区间根的分步求解. 师:二次方程的根是如何分布的? 解得 师:很好,生3通过深刻理解题意,迅速找到了区间根满足的条件. 评注此解法体现了方程的根与函数零点的联系,以及辨别问题与问题之间的区别和联系.培养学生的解题应变能力,注重引导学生从“形”的角度进行思考,抓住“在区间(x1,x2)上恰有3个正整数”这个条件,观察其图像的结构特征,利用数形结合思想再将其转化为二次方程区间根的分布问题. 2.2改造命题,深化探究意识 变式2已知函数f(x)=lg[3tx2+(3-7t)x+4]的值域为R,求实数t的取值范围. 解得 师:对生4的解法有无异议? 生5:老师,他求解的应该是定义域为R时t的范围,故答案不正确. (其他学生也赞同生5的说法.) 师:很好,那么对值域为R时应该怎么求解呢? 生6:老师,我是这样想的:令μ(x)=3tx2+(3-7t)x+4,由对数函数的性质可知:要使μ(x)能取到一切正实数,才能满足值域为R.当t=0时,显然满足题意,当t≠0时, 生7:老师,我有个困惑,为什么要使函数μ(x)能取到一切正实数呢? (笔者观察了一下,有一部分学生也存在这样的疑惑.) 师:这个问题问得好,谁来帮助他解决一下. 生8:由于函数y=lgx(其中x>0)的值域为R,当且仅当x能取到一切正实数,否则值域不为R,即μ(x)能取到一切正实数,函数μ(x)的图像与x轴恒有交点.若μ(x)的图像与x轴没有交点,则 即 (此时,教室里响起一片掌声.) 评注将命题改造,体现知识和方法的纵横联系和灵活运用.依据学生的思维特点,对命题进行恰当的变式,不但调动了学生学习数学的主观能动性,还能进一步深化对知识的理解和对解法的探究.2.3变存在型,增强探究能力 变式3已知函数f(x)=3tx2+(3-7t)x+4(其中t>0).是否存在整数a,b(其中a,b是常数,且a 生9:假设存在满足题意的a,b,则必有f(x)min≥a. 师:你是如何判断f(x)min≥a? 生9:否则,不等式a≤f(x)≤b的解集是2个关于对称轴对称的区间的并集,与题意矛盾. 师:很好,那么如何求解呢? 生10:不等式a≤f(x)≤b的解集为{x|a≤x≤b}等价于 由f(b)=b,得 (1) 因为a,b∈Z,所以 (2) 由式(2)得 且t>0,故t=3.将t=3代入式(1),得 9b2-18b+4=0, 综上可知,不存在整数a,b,使得关于x的不等式a≤f(x)≤b的解集为{x|a≤x≤b}. 评注求解存在性问题,首先假设存在,再根据题意求解.本题的二次不等式a≤f(x)≤b不是被解出来的,而是通过观察、思考二次函数的图像分析出来的,这正是“多思少算”思想的应用,也是高考考查学生分析、解决问题能力的一个重要方向,而这种能力在一定意义上讲比数学知识和技法更重要.要想培养这种能力,必须具有坚实的基础知识和掌握解决问题的相关技巧和方法. 2.4反客为主,掌握探究方法 变式4已知t∈R,函数f(x)=3tx2+(3-7t)x+4,当t∈[1,2]时,f(x)>0恒成立,求实数x的取值范围. 生11:已知t的取值范围,可以将函数f(x)=3tx2+(3-7t)x+4,改为关于变量t的函数g(t)=3tx2+(3-7t)x+4求解. 师:很好,那么如何求解呢? 生11:由g(t)=3tx2+(3-7t)x+4=(3x2-7x)t+3x+4,转化为关于变量t的一次函数,即当t∈[1,2]时,g(t)>0恒成立,得 师:非常棒!解题简捷、美观、迅速,可见方法的选择对解题是非常关键的. 评注此类型的问题主要考查学生处理问题的机智变通能力.实际上是考查多元不等式的恒成立问题,关键要掌握该类问题的解法.该题以t为主元,转化为求一次函数的最小值大于0恒成立的问题,其优点是一次函数比二次函数更容易求解.由此可以看出,在含有2个或2个以上字母的问题中,首先要根据题意适当选取其中一个作为主元,而其余的作为辅元,区分主次,抓住问题的要害,将复杂问题简单化;然后再通过合理构造函数,转化为求函数的最值问题.很多多元不等式问题都可以巧妙地构造辅助函数求解,使得原本扑朔迷离的问题变得直观明了,变得可程序化.因此在教学中应该重视这种方法的引导和渗透,同时还要加强训练,及时归纳总结,才有利于方法的掌握和运用[2]. 3.1运用变式教学调动学生学习的主动性 学生的数学学习活动不应只限于接受、记忆、模仿和练习,高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的其他方式.这些方式有助于发挥学生学习的主动性,使学生的学习过程成为在教师引导下的“再创造”过程[3].在新课程理念指导下对习题的变式教学,不但要增强课本习题的辐射功能,而且还要有效改变学生被动接受知识的局面,激发学生学习的主动性.借助于一题多用、多题重组等方式设计变式问题,不仅具有丰富的背景知识,而且渗透着明确的信息意图.变式教学是一种思维对话的学习形式,应不断追求立足于教材、唤发自主、善待差异、体现学生的主体地位,调动学生的主观能动性,激活其原有认知结构中适当的观念和感性经验,调动起学生有意义的学习心向,从而产生主动参与学习的动力,在思维对话中让变式教学更具有价值和意义. 3.2运用变式教学培养学生思维的深刻性 在习题教学过程中,应引导学生从不同的视角对原问题进行变式探究,拓展学生的知识视野和增强学生的探究意识.要想通过变式教学培养学生思维的深刻性,必须引导学生在思维对话中对变式问题不断反思,不但要对知识层面反思,而且要对知识形成过程反思;不但要对解决问题的途径和方法反思,而且要对蕴藏在现象背后的实质反思,意识到寻常现象中的非常之处.同时在变式教学探究过程中还需要师生分享彼此的思考、经验和知识,交流彼此的情感、体验与观念,丰富教学内容,求得新的发现,从而使变式教学在思维对话中成为一个发展的、增值的、生成的过程. 顾泠沅先生说过:变式教学也是不断发展和变化着的,我们要用发展的眼光来看变式教学,要做到更新问题背景、更新知识考点、更新问题发展方向的研究,最重要的是更新教师的教学观念,这样的教学才是有效的.因此,教师要不断更新观念,真正成为学生学习的引导者,通过习题变式教学,不仅使学生所学的知识达到融会贯通,而且让学生在习题变式探究教学中增强学习的信心、体验成功的快乐和感受数学的魅力.更重要的是通过思维对话,让学生释放出无穷的智慧,在共享中得到升华. [1]单墫.普通高中课程标准实验教科书·数学1(必修)[M].苏州:江苏凤凰教育出版社,2015. [2]郭建华.例谈解题中“辅助元”的构造[J].高中数学教与学,2014(11):22-24. [3]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003. �2016-04-27; 2016-06-03 江苏省教育科学“十二五”规划课题(D/2013/02/445) 郭建华(1982-),男,安徽宿州人,中学一级教师.研究方向:数学教育. O122.1 A 1003-6407(2016)10-06-04
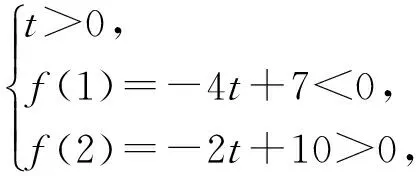
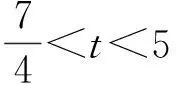
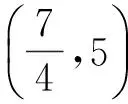
2 关注变式,提升能力
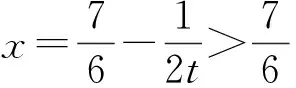
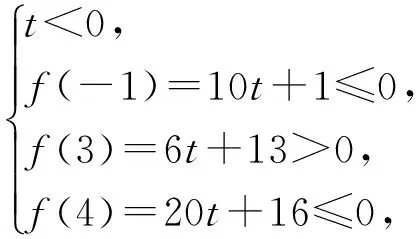
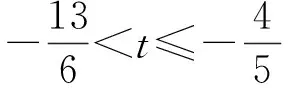
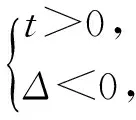
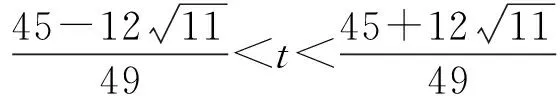
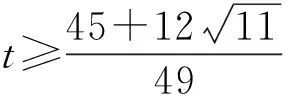
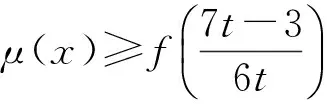
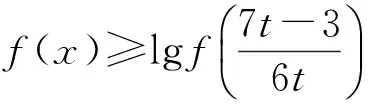
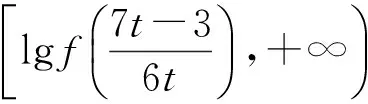


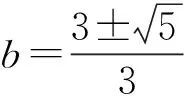
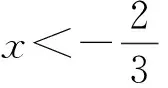
3 教学感悟
