对角占优矩阵的行列式估计

赵建兴，　桑彩丽

(贵州民族大学 理学院　贵州 贵阳 550025)



对角占优矩阵的行列式估计

赵建兴，桑彩丽

(贵州民族大学 理学院贵州 贵阳 550025)

针对对角占优矩阵的行列式估计问题，首先利用严格对角占优矩阵A的元素给出逆矩阵A-1的主对角元的上下界，然后利用逐次降阶法和递归法给出A的行列式的单调递增的下界序列和单调递减的上界序列，改进了一些已有结果. 随后将此方法推广，从而得到对角占优矩阵的行列式的上下界序列. 最后通过数值算例验证理论结果，数值算例表明所得估计在某些情况下能达到真值且比现有结果精确.

矩阵； 对角占优； 行列式； 降阶法； 估计

0　引言

在科学与工程计算问题中有大量的计算问题直接或间接地表现为矩阵计算的形式，例如解线性矩阵方程、线性矩阵不等式[1-2]、求逆矩阵的无穷范数[3]及求矩阵特征值等问题. 因此自然会有这样的问题，是否能有某种方法来判断矩阵的奇异性，并在非奇异的情况下估计出行列式值的上下界.该下界在一定程度上反映了矩阵非奇异程度，且在矩阵的特征值下界和P条件数的估计中经常用到[4-5],文献[4]给出了严格对角占优矩阵的行列式的下界估计式.文献[5]利用矩阵上三角元素给出了对角占优矩阵的行列式的下界估计式.文献[6]利用矩阵上三角元素给出了严格对角占优矩阵的行列式的上下界估计式.文献[7-8]利用不同的方法改进了文献[6]的结果.文献[9]利用矩阵下三角元素给出了严格对角占优矩阵的行列式的上下界估计式.文献[10]给出了弱链对角占优矩阵的行列式的上下界估计式.文献[11]改进了文献[7,9]的结果，并给出其他几类非奇异H-矩阵行列式的估计式. 本文利用矩阵的逆元素估计、逐次降阶法及递归法, 给出了严格对角占优矩阵和对角占优矩阵的行列式的收敛的上下界序列, 在一定条件下改进了文献[4-9,11]的相关结果, 并用数值算例验证了文中结果.

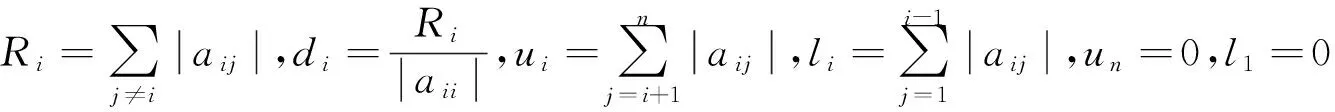
注1由定义1易知SDn⊂CDn⊂Hn.由文献[7]知，若实矩阵A=(aij)∈Hn,且aii>0,i∈N,则det A>0.

引理1[8]若A=(aij)∈SDn，则A-1=(αij)存在, 且对任意的i∈N及某一j≠i,有

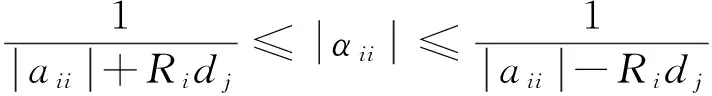
对于严格对角占优矩阵的行列式估计,Ostrowski[4]给出如下结果，设A∈SDn,则

(1)

文献[5]给出了对角占优矩阵行列式的下界估计，设A∈Dn，则

(2)

文献[6]改进了(1)式，并给出结果，设A∈SDn,则

(3)

文献[7]改进了(3)式，并提出结果，设A∈SDn,则

(4)

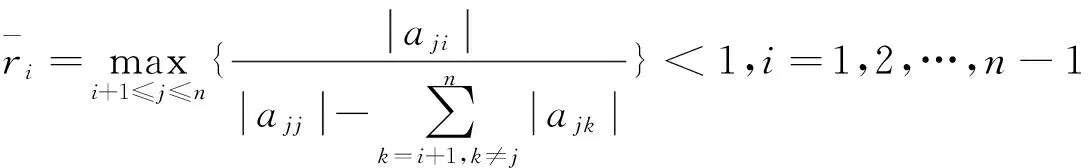
文献[8]改进了(3)式，并给出结果，设A∈SDn,则

(5)

文献[9]改进了(1)式，并提出另一结果，设A∈SDn,则

(6)

文献[10]改进了(4)式，并给出如下结果，设A∈CDn,则

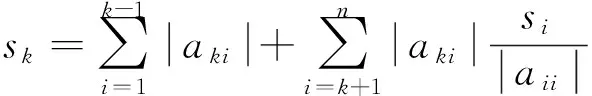
文献[11]改进了(4)式，并给出如下结果，设A∈SDn,则

(7)

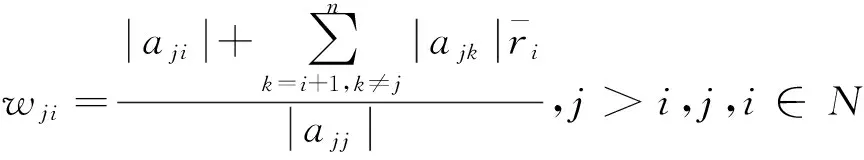
1　主要结果

设A=[aij]∈Rn×n,aii≠0.∀i,j,k∈N,j≠i,t=1,2,…,令

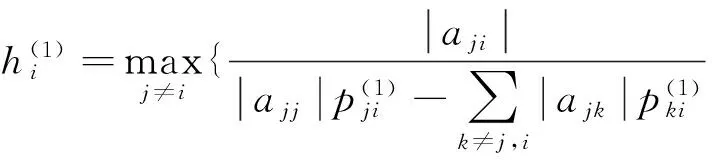
引理3设A=(aij)∈SDn, 则A-1=(αij)存在, 且

证明对于∀i,j∈N,j≠i,t=1,2,…,设ε>0,令

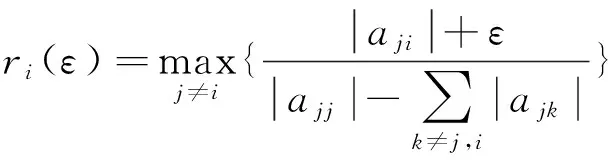
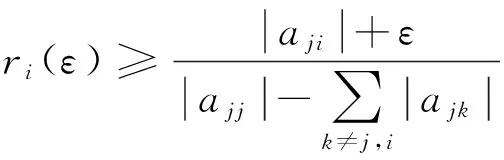
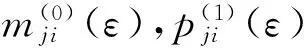
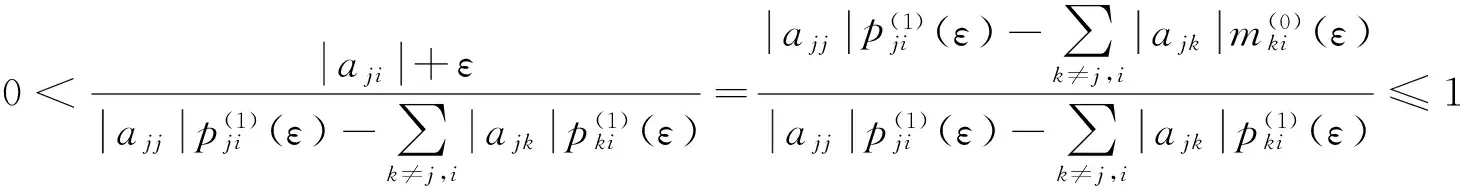
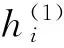
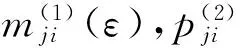
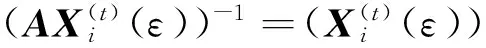
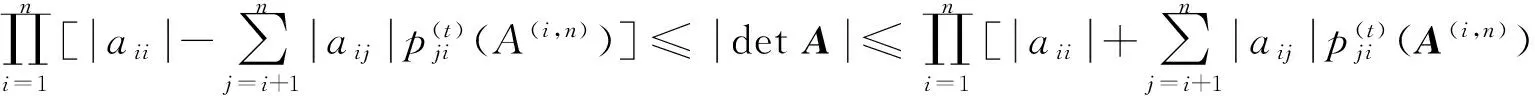
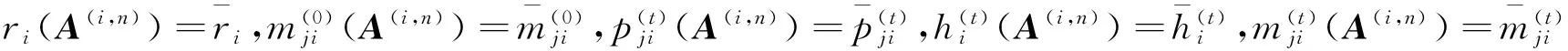
定理3设A=(aij)∈SDn, 则对任意t=1,2,…,

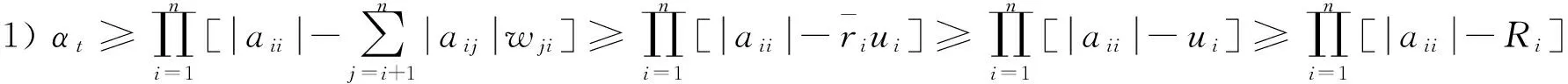
若定理3中严格对角占优矩阵A为对称矩阵，易得如下定理，

定理4设对称矩阵A=(aij)∈SDn, 则对任意t=1,2,…,

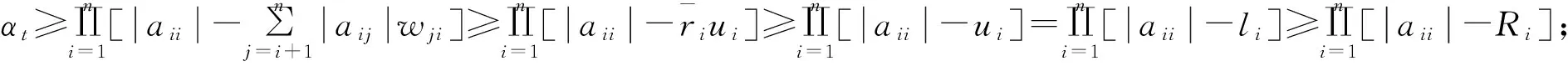
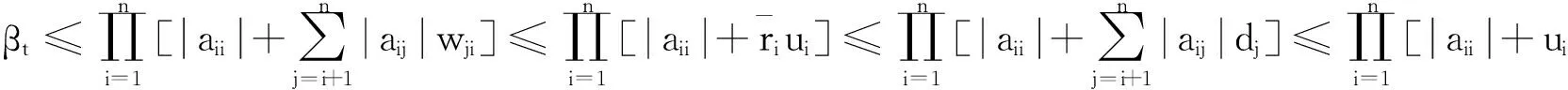
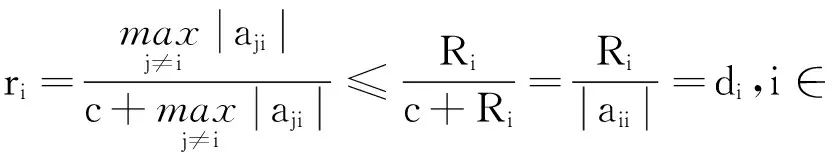
注2由定理3、定理4和定理5知定理1在一定条件下改进了式(1)～(7).若A∈Dn,则∀ε>0,A+εIn∈SDn.将A+εIn应用定理1并令ε→0,根据连续性，可得.

由定理6和注1可得如下推论1.

推论1若实矩阵A=(aij)∈Dn,且aii>0,i∈N,则αt≤detA≤βt,t=1,2,….

2　数值算例

本小节给出两个数值算例验证第二部分的结果.

例1设

易知A∈SD10.由MATLAB7.1计算得det(A)=3.304 3e+010.在定理1中取迭代总次数为10, 由定理1和文献[4-11]中相关结论得到的数值结果在表1中列出，其中t表示迭代次数.

注3从表1可以看出:

1)由定理1得到的det(A)的包含区间优于由文[4-11]中相关结果得到的det(A)的包含区间；

2)由定理1得到的det(A)的包含区间是不断缩小的；

3)由定理1得到的det(A)包含区间能有效地逼近det(A)的真值.

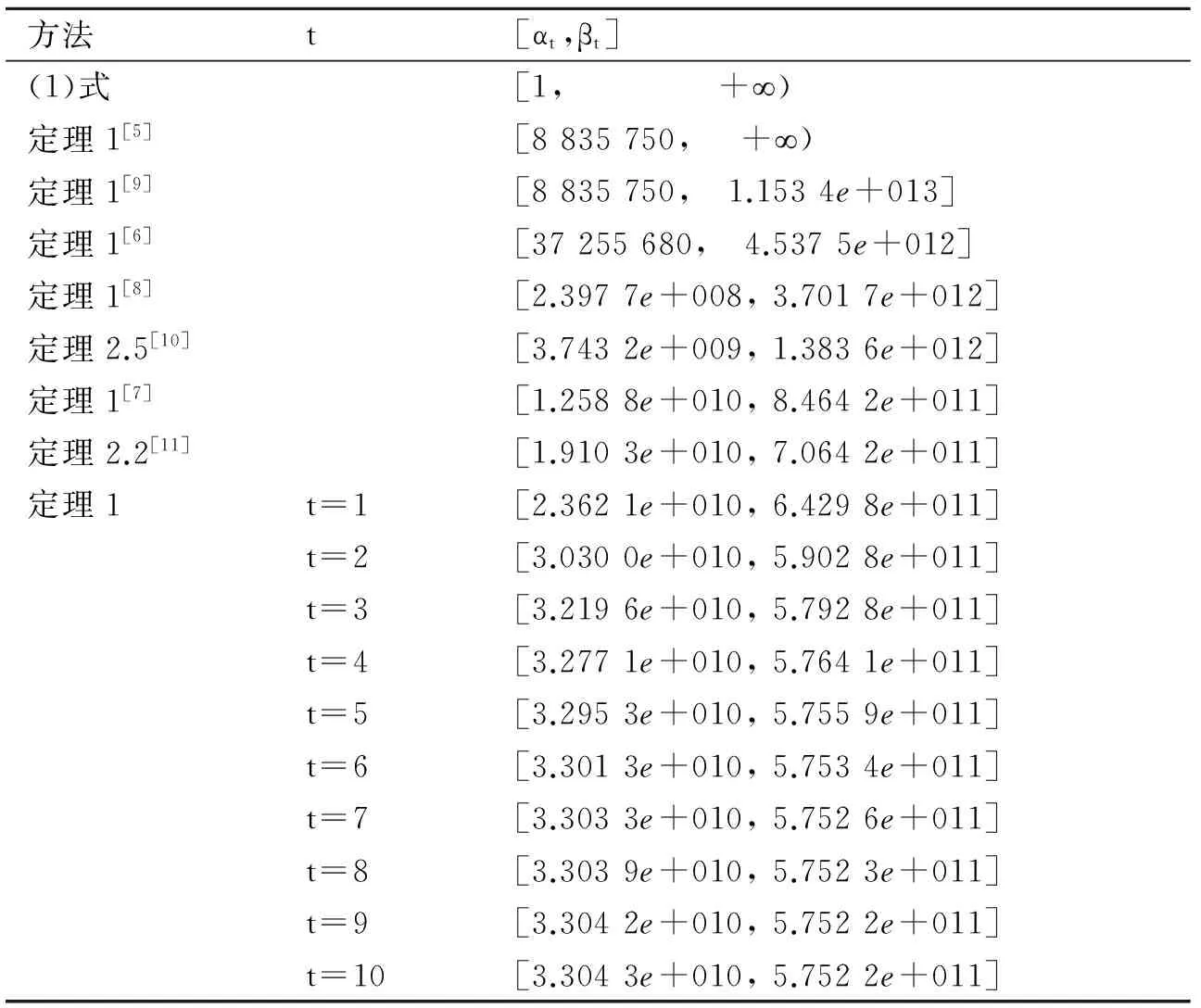
表1　det(A)的包含区间Tab.1　 The scope of det(A)

[1]贾利新,张小勇,周世国.几类线性矩阵方程的显式解[J]. 郑州大学学报(理学版), 2015, 47(2): 24-26.

[2]王岩岩,童艳春,刘伟,等.具有时变传输周期的奇异网络化系统鲁棒控制[J].信阳师范学院学报(自然科学版),2016,29(1):13-16.

[4]OSTROWSKIAM.Surladeterminationdesbornsinterieurespouruneclassdesdeterminants[J].BullSciMath,1937,61(2):19-32.

[5]石钟慈,王伯英.某些类矩阵的行列式,特征值以及条件数界限的若干估计[J].数学学报，1965,15(3):326-341.

[6]PRICEGB.Boundsfordeterminantswithdominantprincipaldiagonal[J].ProceedingsoftheAmerMathSoc,1951,2(3):497-502.

[7]HUANGTZ,LIUXP.Estimationsforcertaindeterminants[J].Computersandmathematicswithapplications,2005,50(10):1677-1684.

[8]高琴,吴春梅,庄光明,等.关于行列式估计的一个注记[J].聊城大学学报(自然科学版),2009,22(1):28-31.

[9]冯天祥,刘学飞.严格对角占优矩阵的行列式估计[J].数学杂志,2008,28(6):673-676.

[10]LIW,CHENYM.Somenewtwo-sidedboundsfordeterminantsofdiagonallydominantmatrices[J].JInequalAppl，2012,61:1-9.

[11]徐仲,黄政阁,陆全.几类非奇H-矩阵的行列式估计[J].应用数学,2015,28(3):692-700.

[12]张俊丽,韩贵春.一类非奇异H-矩阵的迭代判定准则[J].河南科技大学学报(自然科学版),2016,37(1):88-91.

(责任编辑：方惠敏)

EstimatesofDeterminantsforDiagonallyDominantMatrices

ZHAOJianxing,SANGCaili

(College of Science, Guizhou Minzu University, Guiyang 550025, China)

Forestimatesofthedeterminantofdiagonallydominantmatrices,atfirst,somelowerandupperboundsofthemaindiagonalelementsofA-1weregivenbyusingtheelementsofastrictlydiagonallydominantmatrixA.Next,monotoneincreasingsequenceoflowerboundsandmonotonedecreasingsequenceofupperboundsofdeterminantofAweregivenbyusingsuccessivereductionandrecursivemethods.Thesesequencesresultedionimprovementofsomeexistingresults,andthenwereappliedtheupperandlowerboundsofdeterminantofdiagonallydominantmatrices.Finally,numericalexamplesweregiventoverifythetheoreticalresults.Numercialexamplesshowedthatthepresentestimatescouldreachthetruevalueofthedeterminantinsomecasesandweremoreaccuratethantheexistingresults.

matrix；diagonallydominant；determinant；reduction；estimate

2016-02-09

国家自然科学基金资助项目(11361074, 11501141)；贵州省科学技术基金资助项目(黔科合J字[2015]2073号)；贵州民族大学引进人才科研项目(15XRY003)；贵州民族大学科研项目(15XJS009).

赵建兴(1981—)，男，山东济宁人，副教授，主要从事数值代数研究，E-mail: zjx810204@163.com．

O151.21

A

1671-6841(2016)03-0032-07

10.13705/j.issn.1671-6841.2016037

引用本文：赵建兴，桑彩丽．对角占优矩阵的行列式估计[J]．郑州大学学报(理学版)，2016，48(3)：32-38．