多粒度广义L-模糊可变精度粗糙集

薛占熬,　袁艺林,　辛现伟,　司小朦

(1.河南师范大学 计算机与信息工程学院　河南 新乡453007; 2.“智慧商务与物联网技术”河南省工程实验室　河南 新乡453007)



多粒度广义L-模糊可变精度粗糙集

薛占熬1,2,袁艺林1,2,辛现伟1,2,司小朦1,2

(1.河南师范大学 计算机与信息工程学院河南 新乡453007; 2.“智慧商务与物联网技术”河南省工程实验室河南 新乡453007)

为了更有效地处理不精确性问题，将模糊变精度粗糙集与多粒度相结合，成为研究的热点.在不可交换的广义剩余格的基础上，定义了基于L-模糊近似空间的广义L-模糊可变精度粗糙集中的左下(右下)和左上(右上)近似算子.然后，结合多粒度，给出了基于不可交换的广义剩余格的多粒度L-模糊可变精度粗糙集及其近似算子，研讨了它们的一些性质.该研究在变精度粗糙集研究中具有一定的理论价值，提供了一种新方法，能更加精确地解决实际中的不精确性问题.

多粒度； 广义剩余格； L-模糊集； L-模糊近似空间； 广义L-模糊可变精度粗糙集

0　引言

粗糙集理论是Pawlak于1982年提出[1]，用于数据分析和智能信息处理的理论，在许多领域中有着广泛应用[2-5].粗糙集理论作为一种处理不精确、不一致、不完整信息的数学工具，与模糊集理论具有很强的互补性.经典粗糙集模型是建立在等价关系之上的，但等价关系过于严格的约束条件，限制了粗糙集的应用领域，因此广义化粗糙集就成为研究的热点问题并得到了快速发展.文献[6]提出了模糊粗糙集和粗糙模糊集，有学者通过引入不同的模糊逻辑算子和二元关系对模糊粗糙集进行研究[7-9].文献[10-13]提出了L-模糊集和基于不同模糊逻辑算子和二元关系的L-模糊粗糙集模型.文献[14]提出了变精度粗糙集以解决模糊粗糙集对错分和干扰过于敏感的问题，但用于处理真实数据集时，效果并不理想.因此，将模糊粗糙集和变精度粗糙集相结合，来处理真实数据具有重要的研究价值.文献[15]将模糊粗糙集和变精度粗糙集结合，提出了模糊变精度粗糙集模型.文献[16]提出了基于可交换的剩余格的L-模糊可变精度粗糙集模型.然而，对L-模糊可变精度粗糙集和多粒度粗糙集结合的研究还比较少，有必要对此进行研究.

文献[16]对基于可交换剩余格的L-模糊可变精度粗糙集模型进行了定义，并展开了讨论，但由于剩余格是可交换的，具有一定局限性，对不可交换的问题难以解决.本文在文献[16]的基础上，将广义剩余格定义在不可交换情况，结合L-模糊集与L-模糊关系，提出了广义L-可变精度模糊粗糙集的概念，定义了两对不同于文献[16]的广义L-模糊可变精度粗糙的左下(右下)和左上(右上)近似算子.然后，结合多粒度，提出了基于不可交换的多粒度广义L-可变精度粗糙集及近似算子，研讨了它们的一些性质.

1　基础知识

1.1广义剩余格

1) (L,∧,∨,0,1)是一个有界格，最小元素为0，最大元素为1；

2) (L,⊗,Τ)是一个独异点(幺半群)；

1) 若⊗可交换(不可交换)，则广义剩余格可交换(不可交换)；

2) 当Τ=1时，广义剩余格可积；

3) 若基本格(L,∧,∨,0,1)为完备的，则广义剩余格完备.

a⊗(b∨c)=(a⊗b)∨(a⊗c)，(b∨c)⊗a=(b⊗a)∨(c⊗a),

0⊗a=0，a⊗0=0,

需注意，并不是对∀a,b∈L都有a⊗b≤a∧b成立，若广义剩余格不可积，则它就不成立.

(1)

a⊗(b∧c)≤b∧(a⊗c)，(b∧c)⊗a≤b∧(c⊗a).

(2)

证明式(1) 由定理1、定理2，得

式(2) 由定理1，定理2，得

因此，根据定义1，得a⊗(b∧c)≤b∧(a⊗c).同理可证，(b∧c)⊗a≤b∧(c⊗a).

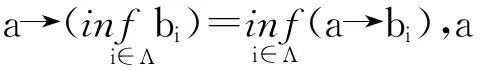
定义3[19]对映射N1:LL,N2:LL，(N1,N2)称为弱否定对，如果满足下列条件：

l0=r0=1，l1=r1=0,

(3)

lb≤la，rb≤ra,a≤b，

(4)

l(ra)≥a，r(la)≥a,

(5)

l(a∧b)=la∨lb,l(a∨b)=la∧lb,

(6)

r(a∧b)=ra∨rb，r(a∨b)=ra∧rb,

(7)

a→lb=l(a⊗b)，arb=r(b⊗a),

(8)

a→b≤lbla，ab≤rb →ra,

(9)

(10)

l(ab)≥(lb⊗a)，r(a→b)≥(a⊗rb),

(11)

(lai)，(rai),

(12)

(lai)，(rai).

(13)

证明式(3)～(5)根据定理1、2和5容易得证，略.

设∀a,b∈L，若a≤b，则a∨b=b，且a∧b=a.

式(7) 证明方法同式(6).

式(9)和式(10) 根据定理1容易得证，略.

式(12)和式(13) 根据定理4容易得证，略.

1.2L-模糊集与L-模糊关系

(A∩B)(x)=A(x)∧B(x)，(A∪B)(x)=A(x)∨B(x),(A→B)(x)=A(x)→B(x)，

对∀x∈X，若A(x)≤B(x)，简写为A⊆B.

对∀R∈LU×W，当∀x∈U,y∈W，L-模糊关系R-1定义为R-1(x,y)=R(y,x).当U=W时，称R是U上的L-模糊关系.

1.3多粒度粗糙集

多粒度粗糙集不同于Pawlak粗糙集，因为前者是建立在不可分辨关系簇的基础上的，而后者则只是利用单一分辨关系.

定义5[21]I是一信息表，且A1,A2,…,Am⊆AT,∀X⊆U，乐观多粒度上下近似表示为：

其中:[x]Ai(1 ≤ i ≤ m)是属性集Ai中x的等价类，～X是X的补.

命题1[21]I是一信息表，且A1,A2,…,Am⊆AT,∀X⊆U，得

证明过程参考文献[21].

定义6[21]I是一信息表，且A1,A2,…,Am⊆AT,∀X⊆U，悲观多粒度上下近似表示为：

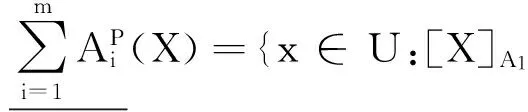
命题2[21]I是一信息表，且A1,A2,…,Am⊆AT,∀X⊆U，得

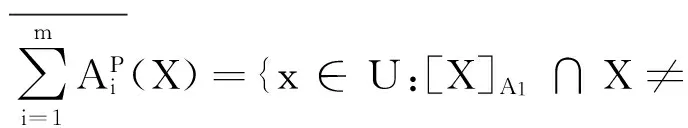
证明过程参考文献[21].

2　多粒度L-模糊可变精度粗糙集

本节中将广义L-模糊可变精度粗糙集与多粒度相结合，对上下近似算子进行粒度化研究.

2.1广义L-模糊可变精度粗糙集

在广义剩余格不可交换的情况下，提出了广义L-模糊可变精度粗糙集的概念.在L-模糊近似空间内，定义了两对近似算子，用于描述L-模糊近似空间.

设U和W为两个非空论域，R是U×W上的L-模糊关系.三元组(U,W,R)称为L-模糊近似空间.

定义7令(U,W,R)为L-模糊近似空间，且ξ∈L.对∀A∈LW,x∈U,定义4个映射：

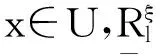
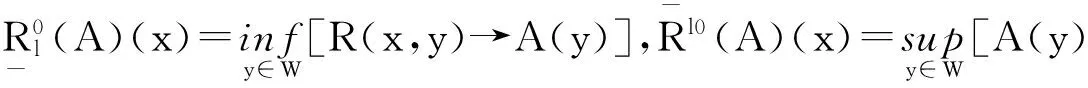
2.2多粒度广义L-模糊可变精度粗糙集

在本节中，结合多粒度，对广义L-模糊可变精度粗糙集进行扩展，给出了多粒度L-模糊可变精度粗糙集的概念，即将广义L-模糊可变精度粗糙集中的左下(右下)和左上(右上)近似算子扩展为多粒度结构，能更加精确地解决实际中的不确定性问题.

下面首先给出多粒度L-模糊可变精度粗糙集的概念，然后讨论其性质.

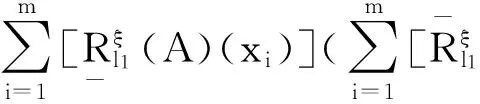
定理7设(U,W,R)是L-模糊近似空间.对∀A∈L,xi∈U,(i=1,2,…,m)，满足如下性质：

证明根据定义8，容易证明，略.

定理8设(U,W,R)是L-模糊近似空间.对∀A∈L,xi∈U,(i=1,2,…,m)，当A⊆B时，满足如下性质：

证明根据定义8，容易证明，略.

定理9设(U,W,R)是L-模糊近似空间.对∀A∈L,xi∈U,(i=1,2,…,m)，R,Q是U×W上的L-模糊关系，当Q⊆R，满足如下性质：

证明根据定义8，容易证明，略.

定理10设(U,W,R)是L-模糊近似空间.对∀A∈L,xi∈U,(i=1,2,…,m)，满足如下性质：

(14)

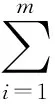
(15)

(16)

(17)

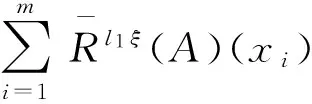
(18)

(19)

证明这里仅证明式(14)中第一公式，第二公式证明类似.对∀A∈L,xi∈U,(i=1,2,…,m)，

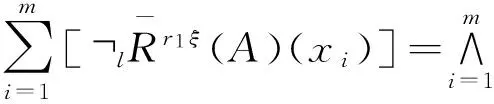
同理可证式(15).

这里仅证明式(16)中第一公式，第二公式证明类似.对∀A∈L,xi∈U,(i=1,2,…,m)，

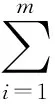
同理可证式(17)～(19).

定理11设(U,W,R)是一个L-模糊近似空间.对∀A∈L,xi∈U,(i=1,2,…,m)，满足如下性质：

(20)

(21)

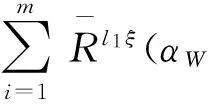
(22)

(23)

证明 这里仅证明式(20)中第一公式，第二公式证明类似.对∀A∈L,xi∈U,(i=1,2,…,m),

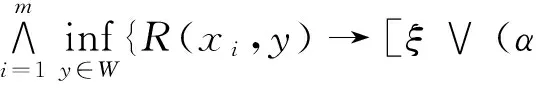
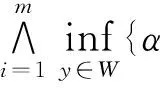
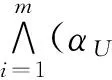
同理可证式(21).

这里仅证明式(22)中第一公式，第二公式证明类似.对∀A∈L,xi∈U,(i=1,2,…,m)，

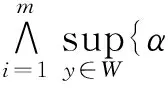
同理可证式(23).

定理12设(U,W,R)是L-模糊近似空间.对∀A∈L,xi∈U,(i=1,2,…,m)，满足如下性质：

(24)

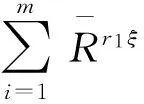
(25)

证明 这里仅证明式(24)中第一公式，第二公式证明类似.对∀A∈L,xi∈U,(i=1,2,…,m),

同理可证式(25).

3　结束语

首先在L-模糊近似空间中，运用不可交换的广义剩余格，构建了广义L-模糊可变精度粗糙集的左下(左上)和右下(右上)近似算子，然后，结合多粒度，提出了多粒度广义L-模糊可变精度的左下(左上)和右下(右上)近似算子，证明其一系列性质.本文将广义L-模糊可变精度粗糙集中的两对上下近似进一步粒化，能对实际的不确定性数据进行细化与求解.

[1]PAWLAK Z. Rough set[J].International journal of computer & information sciences, 1982,11(5):341-356.

[2]朱永明.基于粗糙集理论的股市预测研究[J]. 郑州大学学报(理学版),2009,41(4):45-49.

[3]ABU-DONIA H M. Multi knowledge based on two universal sets and its application[J]. Knowledge-based system, 2010,23(2):110-115.

[4]胡静,曹先彬,王煦法.基于相容粗糙集的图形图像信息预检索[J].计算机辅助设计与图形学学报,2002,14(3):242-246.

[5]LIU G L. Rough set theory based on two universal sets and its application[J]. Knowledge-based system, 2010,23(2):110-115.

[6]DUBOIS D, PRADE H. Rough fuzzy sets and fuzzy rough sets[J]. Internal journal of general system, 1990,17(2):191-208.

[7]RADZILNWSLA A M, KERRE E E. A comparative study of fuzzy rough sets[J]. Fuzzy sets and system, 2002,126(2):137-155.

[8]GONG Z T, SUN B S, CHEN D G. Rough sets theory for the interval-valued fuzzy information systems[J]. Information sciences, 2008,178(13):2794-2815.

[9]ZHANG H Y, ZHANG W X, WU W Z. On characterization of generalized intervaL-valued fuzzy rough sets on two universities of discourse[J]. International journal of approximation reasoning, 2009,51(1):56-70.

[10]HAO J, LI Q. The relationship betweenL-fuzzy rough set andL-topology[J]. Fuzzy sets and system, 2011,178(1):74-83.

[11]LIU G L. Generalized rough sets over fuzzy lattices[J]. Information sciences, 2008,178(6):1651-1662.

[12]MA Z M, HU B Q. Topological and lattices structures ofL-fuzzy rough sets determined by lower and upper sets[J].Information sciences,2013,218(1):194-204.

[13]WANG C Y, HU B Q. Fuzzy rough sets based on generalized residuated lattices[J]. Information sciences, 2013,248(21):31-49.

[14]ZIARKO W. Variable precision rough set model[J]. Journal of computer and system sciences, 1993,46(1):39-59.

[15]ZHAO S, TSANG E C C, CHEN D. The model of fuzzy variable precision rough sets[J]. IEEE transaction on fuzzy system, 2009,17(2):451-467.

[16]ZHAO X R, HU B Q. Fuzzy variable precision rough sets based on residuated lattices[J]. International journal of general system, 2014,44(7):1-23.

[17]BLOUNT K, TSINAKIS C. The structure of residuated lattices[J]. International journal of algebra and computation, 2011,13(4):437-461.

[18]GEORGESCU G, POPESCUB A. Non-commutative fuzzy galois connections[J]. Soft computing, 2003,7(7):458-467.

[19]GEORGESCU G, POPESCUB A. Non-commutative fuzzy structures and pairs of weak negations[J]. Fuzzy sets and system, 2004,143(1):129-155.

[20]GOGUEN J A.L-fuzzy sets[J]. Journal of mathematical analysis and applications,1966,18(1):145-174.

[21]QIAN Y H, ZHANG H, SANG Y, et al. Multi-granulation decision-theoretic rough sets[J]. International journal of approximate reasoning, 2014,55(1):225-237.

[22]RADZIKOWSLA A M, KERRE E E. Fuzzy rough sets based on residuated lattices[J]. Transactions on rough sets Ⅱ, 2004,3135:278-296.

(责任编辑：王浩毅)

Multi-granulation GeneralizedL-fuzzy Variable Precision Rough Set

XUE Zhan’ao1,2, YUAN Yilin1,2, XIN Xianwei1,2, SI Xiaomeng1,2

(1.CollegeofComputerandInformationEngineering,HenanNormalUniversity,Xinxiang453007,China;2.EngineeringTechnologyResearchCenterforComputingIntelligence&DataMiningofHenanProvince,Xinxiang453007,China)

In order to deal with the imprecise problem effectively, the combination of the fuzzy variable precision rough set with multi-granulation has become a research hotspot. Based on the non-commutative generalized residual lattice, the left lower (right lower) and left upper (right upper) approximation operators of generalizedL-fuzzy variable precision rough set were defined in theL-fuzzy approximation space. Then, combing with multi-granulation, multi-granulation generalizedL-fuzzy variable precision rough set and approximation operators were defined, and their properties were explored. The findings of this study explored the research of variable precision rough set, and provided a new method to solve the imprecise problem in practice.

multi-granulation; generalized residuated lattices;L-fuzzy sets;L-fuzzy approximation space; generalizedL-fuzzy variable precision rough set

2016-06-15

国家自然科学基金资助项目(61273018);河南省基础与前沿技术研究项目(132300410174);河南省教育厅项目(14A520082);新乡市重点科技攻关项目(ZG14020).

薛占熬(1963—)，男，河南新乡人，教授，主要从事人工智能基础理论和粗糙集理论研究，E-mail：xuezhanao@163.com.

TP181

A

1671-6841(2016)03-0082-08

10.13705/j.issn.1671-6841.2016095

引用本文:薛占熬,袁艺林,辛现伟，等.多粒度广义L-模糊可变精度粗糙集[J].郑州大学学报(理学版)，2016，48(3)：82-89.