基于多尺度方法的1∶3共振双Hopf分岔分析

王万永，　陈丽娟，　郭　静

(1.河南工程学院 理学院　河南 郑州 451191； 2.郑州铁路职业技术学院 公共教学部　河南 郑州 450052)



基于多尺度方法的1∶3共振双Hopf分岔分析

王万永1，陈丽娟1，郭静2

(1.河南工程学院 理学院河南 郑州 451191； 2.郑州铁路职业技术学院 公共教学部河南 郑州 450052)

利用改进的多尺度方法对一个电路振子模型1∶3共振附近的动力学行为进行了研究.应用该方法得到了系统的复振幅方程，进而得到一个振幅与相位解耦的三维实振幅系统，通过分析实振幅方程的平衡点个数及其稳定性，将系统共振点附近的动力学行为进行分类，发现了双稳态等动力学现象，数值模拟验证了理论结果的正确性.

电路振子； 1∶3共振； 多尺度方法； 分岔

0　引言

在非线性动力学的研究中，内共振由于能够反应系统线性模态之间的相互作用，有着非常重要的研究价值.文献[1]通过研究一个两端固支屈曲梁模型的内共振，构建了该模型在1∶1和1∶3内共振情形下的非线性模态.文献[2]研究了一个悬索模型的1∶2内共振，并讨论了三次非线性和高阶修正项对系统解的影响.文献[3]研究了一个极限环振子系统发生的1∶3共振双Hopf分岔，并研究了非线性对共振附近动力学行为的影响.文献[4]通过利用3∶1内共振的性质设计了一个非线性振动吸振器.文献[5]研究了内共振条件下风力发电机风轮叶片的空气动力学行为.在内共振和双Hopf分岔的研究中，常用的方法有中心流形和规范型方法、多尺度方法、摄动增量法、Liapunov-Schmidt约化和奇异摄动法.这些方法都存在一些问题，例如中心流形方法计算过程复杂，奇异性理论更加数学化，晦涩难懂，而多尺度方法得到的强共振的实振幅方程中，平衡点是非孤立的平衡点[6]，因而使稳定性分析和分岔分析无法进行.在本文的研究中，将应用一种改进的多尺度方法，把1∶3共振的规范型化为一个三维的实振幅系统，进而可以研究系统在共振点附近的动力学行为.

本文以一个电路振子模型为例，利用改进的多尺度方法研究其1∶3共振点附近的动力学行为.其电路示意图如图1所示[7].

其数学模型为[7]：

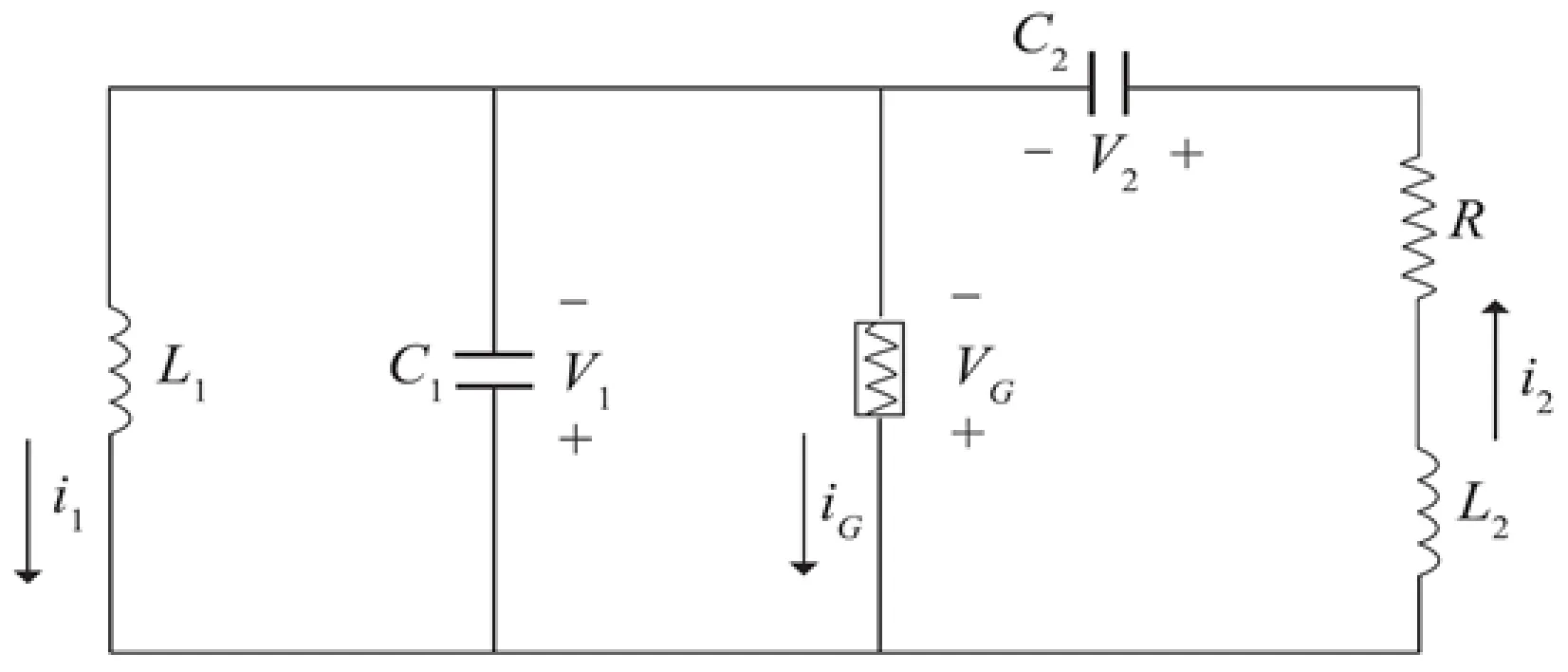
图1　电路振子Fig.1　The electric oscillator；；

(1)

其中：x1=v1，x2=i1，x3=v2，x4=i2是状态变量；η1=1/C1，η2=R，η3=1/L1，ρ1=1/C2，ρ2=1/L2是参数；α1、α2、α3是辅助参数.非线性电路模型的动力学行为是非线性动力学研究的重要内容之一.目前已有不少的文献从实验和理论方面对其进行了研究[8-12]，并发现了次谐波振荡、周期解、概周期解、分岔以及混沌等大量的非线性现象[11].本文将应用改进的多尺度方法对该电路系统的1∶3共振进行研究，计算其振幅方程并分析共振点附近的动力学行为.

1　振幅方程

λ4+(-α1η1+η2ρ2)λ3+(η1η3+η1ρ2-α1η1η2ρ2+ρ1ρ2)λ3+(η1η2η3ρ2-α1η1ρ1ρ2)λ+η1η3ρ1ρ2=0.

(2)

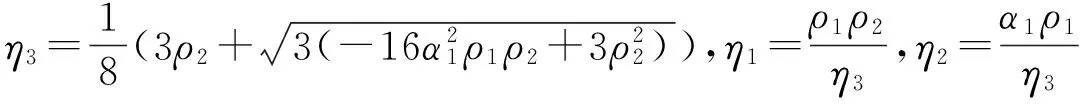
为了得到1∶3共振的规范型方程,将应用改进的多尺度方法对系统(1)进行分析.首先按照如下形式摄动参数

(3)

(4)

其多尺度形式的解具有如下形式

y(t)=εy1(T0,T2)+ε2y2(T0,T2)+ε3y3(T0,T2)+O(ε4).

(5)

将式(3)、(5)带入式(4),并对式(4)的右端进行Taylor展开,令两端ε的各次幂的系数相等,可得

(6)

(7)

(8)

方程(6)的解具有如下形式

y1=A1(T2)p1eiω1T0+A2(T2)p2eiω2T0+c.c.,

(9)

其中：Aj(j=1,2)是复振幅，为时间尺度T2的函数；p1和p2是相应于特征值iω1和iω2的右特征向量；c.c. 表示前面各项的复共轭.将式(9)代入式(7),可求得式(7)的解为

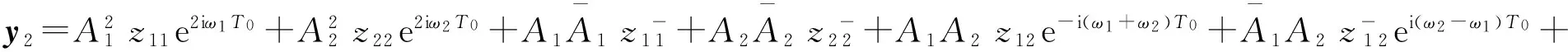
(10)

其中zij是复系数.

将式(9)、(10)代入式(8),令长期项的系数为零,可得到A1和A2关于时间尺度T2导数的两个方程.应用左特征向量消去D2A1和D2A2的系数并吸收参数ε[13],可得

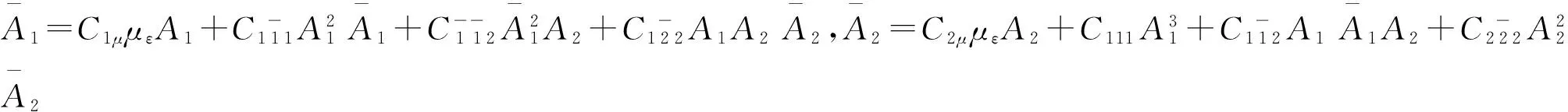
(11)

Cijk和Ciμμε是复系数.在式(11)中，A1和A2为复振幅，为了将式(11)转化为实数振幅方程，通常将A1和A2设为极坐标形式.但是，在强共振条件下，如果将A1和A2设为极坐标形式，将会得到一个实振幅与相位变量耦合的三维系统，其平衡点将是非孤立的平衡点，平衡点的稳定性将无法研究.为了避免这种情况，将复振幅A1和A2设为一种混合形式(极坐标-笛卡尔形式)[13]，

(12)

将式(12)代入式(11),分离其实部和虚部,可得到一个振幅与相位解耦的三维实振幅方程，如下:

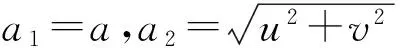
2　动力学行为分析

由前面的分析可知1∶3共振的振幅方程是由3个变量组成的三维系统，并且含有3个分岔参数.为了分

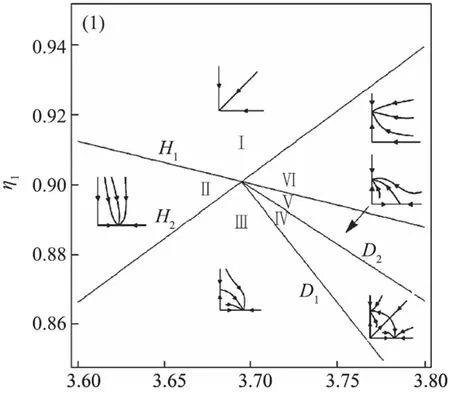
图2　系统(1)在η1-η2平面内的动力学行为分类图和相图Fig.2　The classification of the dynamical behavior and phase portraits of system (1) in the plane of η1-η2

析共振点(η1c，η2c，η3c)附近的动力学行为，可以固定其中一个分岔参数，分析系统在二维参数平面上共振点附近的动力学行为.为此，固定参数η3，在η1-η2平面内对系统的动力学行为进行分类.根据实振幅方程的平衡点个数及每个平衡点稳定性的不同, 将平面η1-η2分为6个不同的区域，如图2所示.在Ⅰ区中，其平凡平衡点E0(0,0)是稳定的平衡点，对应于原系统的原点.当参数进入Ⅱ区，一个稳定的单模态平衡点E1(a10,0)出现，而平凡平衡点E0(0,0)变为不稳定的平衡点.当参数进入Ⅲ区，一个不稳定的平衡点E2(0,a20)出现，而平衡点E1(a10,0)保持其稳定性，平衡点E0(0,0)仍然是不稳定的.在Ⅳ区，一个新的不稳定的双模态平衡点E3(a12,a22)产生，而平衡点E1(a10,0)和E2(0,a20)是稳定的平衡点.在Ⅴ区，双模态平衡点E3(a12,a22)消失，平衡点E1(a10,0)失稳，平衡点E2(0,a20)仍然是稳定的.在Ⅵ区，平衡点E2(0,a20)保持稳定性，平衡点E1(a10,0)消失.其中单模态平衡点E1(a10,0)和E2(0,a20)分别相应于原系统频率为ω1和ω2的周期解，双模态平衡点E3(a12,a22)则相应于原系统的一个概周期解.

为了验证理论分析的正确性，对原系统进行数值模拟，模拟的结果如图3～图8所示.可以发现，当参数在共振点附近变化时，系统出现两个不同频率的周期解，其频率比值接近1∶3.同时在分类图的Ⅳ区，两个不同频率的周期解同时出现，系统出现双稳态现象.

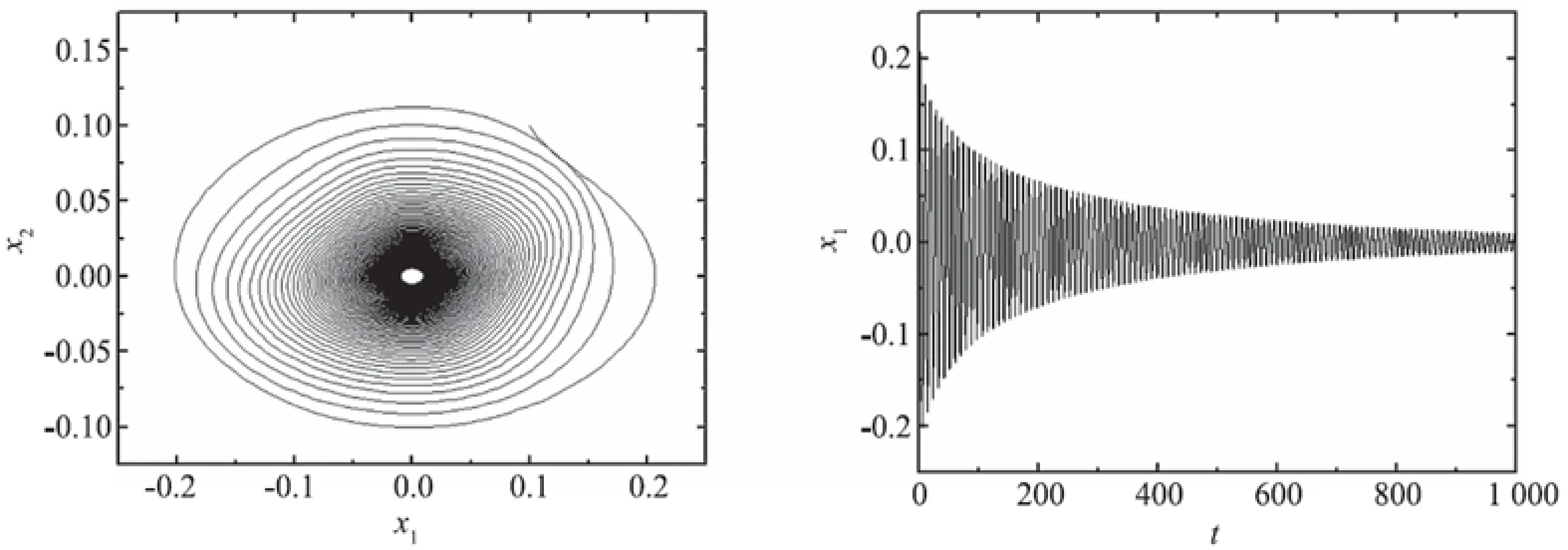
图3　Ⅰ区内稳定平衡点的相图和时间历程图Fig.3　Phase portrait and time history of the stable equilibrium in region Ⅰ

图4　Ⅱ区内周期解的相图和时间历程图Fig.4　Phase portrait and time history of periodic solution in region Ⅱ

图5　Ⅲ区周期解的相图和时间历程图Fig.5　Phase portrait and time history of periodic solution in region Ⅲ

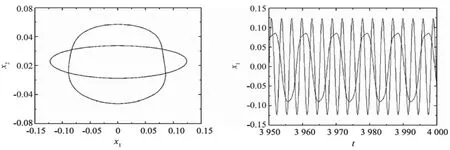
图6　Ⅳ区内双稳态的相图和时间历程图Fig.6　Phase portrait and time history of the bi-stable state in region Ⅳ

图7　Ⅴ区内周期解的相图和时间历程图Fig.7　Phase portrait and time history of periodic solution in region Ⅴ

图8　Ⅵ区内周期解的相图和时间历程图Fig.8　Phase portrait and time history of periodic solution in region Ⅵ

3　总结

本文研究了一个电路振子模型中发生的1∶3共振双Hopf分岔，通过应用改进的多尺度方法得到了该1∶3共振的规范型方程，进而分析其共振点附近的动力学行为，发现了周期解、双稳态等动力学现象，并通过数值模拟验证了结果的正确性.本文在揭示电路振子系统动力学现象的同时，应用了一种研究1∶3共振的新方法，该方法通过应用多尺度方法的过程，并将1∶3共振的复振幅设为一种混合形式，可以得到1∶3共振实振幅系统，从而能够研究共振点附近的动力学行为.

[1]LACARBONARA W，REGA G，NAYFEH A H．Resonant non-linear normal modes．Part I：analytical treatment for structural one-dimensional systems [J]．Int J Non-linear Mech,2003，38(6)：851-872．

[2]LEE C L， PERKINS N C．Nonlinear oscillations of suspended cables containing a two-to-one internal resonance [J]．Nonlinear Dyn，1992，3(6)：465-490.

[3]王万永，陈丽娟．非线性时滞反馈对共振附近动力学行为的影响 [J]．信阳师范学院学报(自然科学版)，2014，27(1)：15-18．

[4]JI J C， ZHANG N．Design of a nonlinear vibration absorber using three-to-one internal resonances [J]．Mech Syst Signal Processing，2014，42(1/2)： 236-246．

[5]LI L,LI Y H,LIU Q K,et al. Flap wise non-linear dynamics of wind turbine blades with both external and internal resonances[J]．Int J Non-Linear Mech，2014，61(1)：1-14．

[6]LUONGO A，DI EGIDIO A，PAOLONE A．On the proper form of the amplitude modulation equations for resonant systems [J]．Nonlinear Dyn，2002，27(3)：237-254．

[7]REVEL G，ALONSO D M，MOIOLA J L．Numerical semi-global analysis of a 1∶2 resonant Hopf-Hopf bifurcation [J]．Physica D-nonlinear phenomena，2012，247(1)：40-53．

[8]徐兴磊，李红．压缩真空态的激发态下介观串并联RLC电路的量子涨落 [J]．郑州大学学报(理学版)，2007，39(1)：67-70．

[9]方天申，董学义．LC串联电路非共振固有振荡与谐波共振的区别 [J]．信阳师范学院学报(自然科学版)，2007，20(4)：429-431．

[10]CHUA L O, WU C W, HUANG A, et al．A universal circuit for studying and generating chaos-Ⅱ：Strange attractors[J]. IEEE T Circuits Sys I, 1993, 40(10): 745-761.

[11]张晓芳，陈章耀，毕勤胜．非线性电路系统动力学的研究进展及展望 [J]．电路与系统学报，2012，17(5)：124-129．

[12]苏利捷，魏兆博，杨广德．单相逆变器共模电磁干扰特性研究 [J]．郑州大学学报(理学版)，2014，46(4)：57-62．

[13]LUONGO A，PAOLONE A，DI EGIDIO A．Multiple timescales analysis for 1∶2 and 1∶3 resonant Hopf bifurcations [J]．Nonlinear dynamics，2003，34(3/4)：269-291．

(责任编辑：方惠敏)

Analysis of 1∶3 Resonant Double Hopf Bifurcation by Using the Method of Multiple Scales

WANG Wanyong1，CHEN Lijuan1，GUO Jing2

(1.CollegeofScience,HenanInstituteofEngineering,Zhengzhou451191,China； 2.DepartmentofPublicTeaching,ZhengzhouRailwayVocationalandTechnicalCollege,Zhengzhou450052,China)

The dynamical behavior near a 1∶3 resonance of an electric oscillator was investigated. By using the method of multiple scale, the complex amplitude equations of the system were obtained. Then a three dimension real amplitude system in which the amplitudes decouple from the phases was given. Analyzing the number of equilibrium and its stability of the real amplitude equation, the dynamical behavior around the resonant point was classified. Some interesting dynamical phenomenon were found, for example,the bistability. Numerical simulations for justifying the theoretical analysis were also provided.

electric oscillator; 1∶3 resonance; the method of multiple scale; bifurcation

2016-03-06

国家自然科学基金资助项目(11302072)；河南省科技厅资助项目(112300410194)；河南教育厅资助项目(12B120004)；郑州市科技局资助项目(20141391)．

王万永(1982—)，男，河南南阳人，讲师，主要从事非线性动力学研究，E-mail: wangwanyong630@163.com．

O175.1

A

1671-6841(2016)03-0023-05

10.13705/j.issn.1671-6841.2016053

引用本文：王万永，陈丽娟，郭静．基于多尺度方法的1∶3共振双Hopf分岔分析[J] ．郑州大学学报(理学版)，2016，48(3)：23-27．