浅谈微积分的应用
2016-10-25金韩中


作者简介:金韩中(1998.05-),男,韩国人,北京拔萃双语学校,高三学生,拔翠双语学校数学兴趣小组组长。
指导老师:池明月(1981.09-),女,朝鲜族,黑龙江鸡西人,北京拔萃双语学校教师,从事中学数学教学,拔翠双语学校数学兴趣小组指导教师。
摘 要:数学很好地锻炼了我们的逻辑思维能力,我们现在能够运用所学的数学知识解决很多问题。数学一直跟随着科学社会的进步而发展,在十七世纪时,人们面临着怎样解决函数曲线长度的求值问题,曲线围成图形面积求值问题,人们借助极限思想,创立了微积分学,微积分的出现很好地解决了上述问题,并且越来广泛地应用到各个领域中。
关键词:微分;导数;定积分;不定积分
中图分类号:O172文献标志码:A文章编号:2095-9214(2016)10-0105-02
一、微积分的产生
从17世纪开始,随着社会的进步和生产力的发展,有許多科学问题需要解决,物理方面的即时速度问题,曲线函数中曲线长度的求值问题,几何中曲线围成图形的面积求值问题等等,这些促使了新的数学思想的产生,“无限细分”以及“无限求和”的思想,最终促使了微积分的产生。
十七世纪初,有数十位科学家对微积分进行了探索,微积分的大量知识已经积累起来了。到了十七世纪后半叶,牛顿主要从运动学的角度出发,独自研究和完成了微积分的创立工作,而莱布尼茨则侧重于从几何学的角度出发,独自研究和完成了微积分的创立工作,两人的研究促使了微积分学的产生。
在十九世纪以前,在微积分的发展过程中,其数学分析的严密性问题一直没有得到解决。柯西极限存在准则为微积分注入了严密性,维尔斯特拉斯,黎曼为积分的完善做出了杰出贡献。
二、微分的几何意义及其应用
微积分是建立在实数,函数和极限的基础上的,包含微分学和积分学。其中微分学主要包括极限理论,导数描述,微分等,积分学主要包括定积分和不定积分。
首先我们要理解到,“极限”在微积分学中引入的必要性,当我们确定一个値时,通过考察这一连串近似值的趋向,确定一连串越来越准确的近似值,最终确定一个量,这就是极限的思想方法①。
其次,导数的概念,导数是指函数在一点处自由变量所引起的函数变化的快慢程度。其本质是利用极限概念对函数进行局部的线性逼近。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率②。
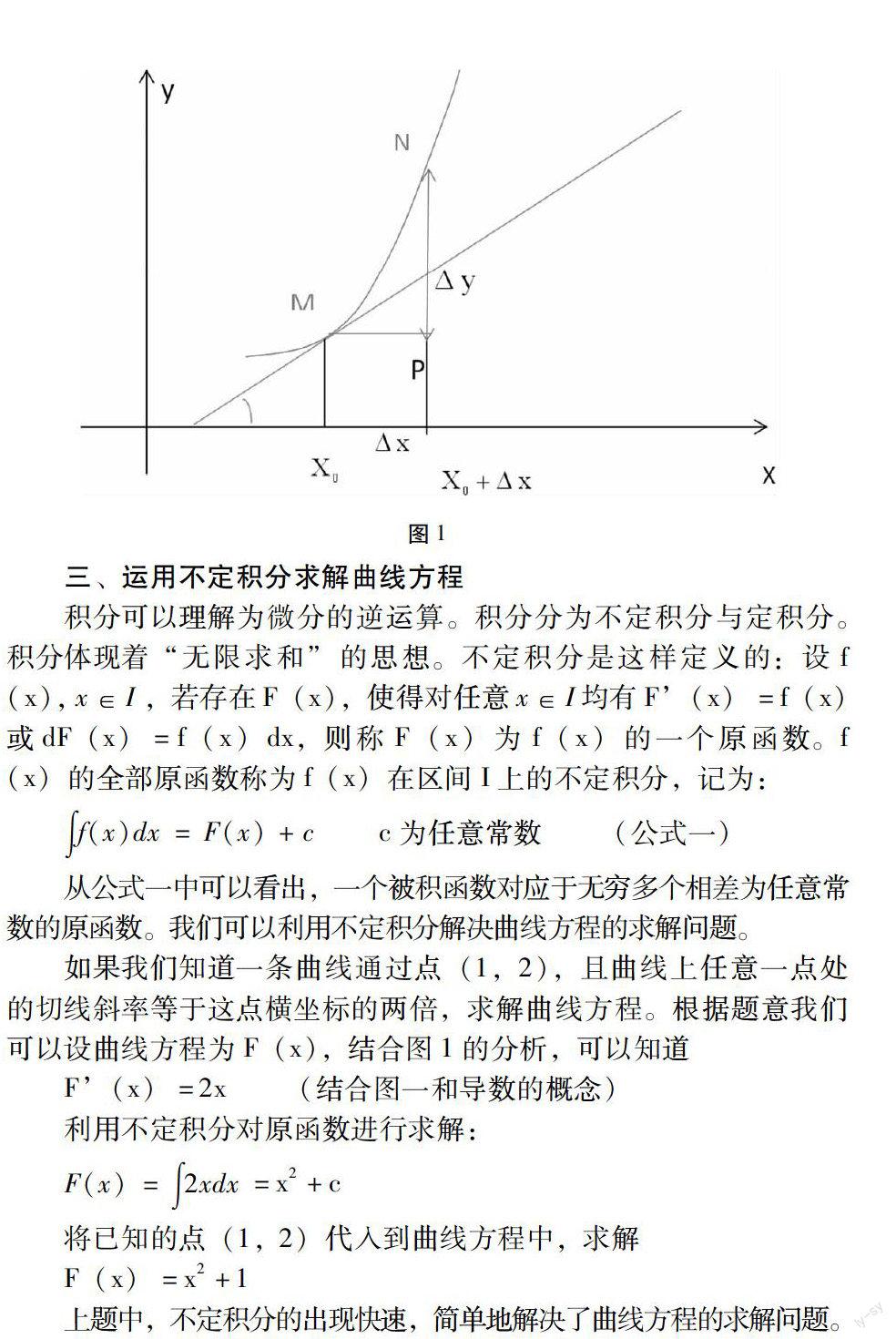
在数学中,微分是对函数的局部变化率的一种线性描述。微分可以近似地描述当函数自变量的取值作足够小的改变时,函数的值是怎样改变的。从微分的几何意义分析(如图1),当Δy是曲线的纵坐标增量时;dy就是切线纵坐标对应的增量,借助极限思想,当Δ x很小时,在点M的附近,切线段MP可近似代替曲线段MN。
从图一中我们可以看处曲线切线的斜率tanα即为函数的导数。
从微分的几何意义可以看出我们可以利用微分解决求曲线长度的问题。微分也可以利用在物理学中,如果一个物体的运动路程与时间的函数为S,则速度函数是s的导数,即V=S。
不只是总产量的问题,复利,年有效收益,连续复利,成本函数,需求函数,消费者剩余,生产者剩余,最大利润等一系列的经济问题都可以通过微积分来解决。
六、小结
从以上例子中,我们看到了微积分在物理学,在曲线函数以及经济学方面的应用。微积分是与实际应用联系着发展起来的,面对科学难题,人们开始借助“不变”来认识“变”,借助极限的思想,从直线形来认识曲线形,从近似认识精确。面对变速直线运动的瞬时速度问题,人们借助极限思想,在小范围内,用匀速代替变速,将瞬时速度定义为平均速度的极限,利用微积分解决变速的问题。
在当今社会,微积分已经越来越广泛地应用到天文学、力学、化学、生物学、工程学、经济学等自然科学、社会科学及应用科学等多个分支中。而计算机的发明更是有助于这些应用的不断发展。
(作者单位:北京拔萃双语学校)
(指导老师:池明月)
注释:
①对于y=nn+1,当n=100时,结果约为0.99,当n=1000时,结果约为0.999。那么利用极限思想,当n无限趋近正无穷,结果就无限趋近1。即n→+∞,y→1
②运动学中,做匀加速直线运动的物体在t时刻的运动速度是Vt=V0+at,对Vt求导,可以得到Vt′=a,即物体速度变化的快慢。
参考文献:
[1]同济大学数学系.高等数学[M].高等教育出版社,2007
[2]龚昇.微积分五讲.科学出版社[M].2004
[3]龚德恩.经济数学基础(微积分)[M].四川人民出版社,2005
