基于教材 谈高考试题—对2016年高考新课标I卷解析几何题的剖析与思考

中国科技大学附属中学（230051）　黄严生



基于教材 谈高考试题—对2016年高考新课标I卷解析几何题的剖析与思考

中国科技大学附属中学（230051）黄严生

近几年高考新课标I理科数学试卷，解析几何是解答题的必考内容，一般试题的难度较大，位置是第20题.今年高考新课标I理科数学试卷第20题的解析几何题，源于课本，高于课本，凸显创新.突出考查了解析几何的本质，考查考生运算求解、分析问题、以及综合运用所学知识解决问题能力，考查数形结合、函数方程、转化与化归等数学思想.笔者将从以下几个方面进行分析.

一、试题解答与剖析

题目 设圆x2+y2+2x-15=0的圆心为A，直线l过点B（1,0）且与x轴不重合，交圆A于C，D两点，过B作AC的平行线交AD于点E.

（I）证明|EA|+|EB|为定值，并写出点E的轨迹方程；

（II）设点E的轨迹为曲线C1，直线l交C1于M，N两点，过B且与l垂直的直线与圆A交于P，Q两点，求四边形MPNQ面积的取值范围.

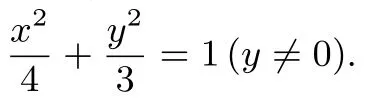
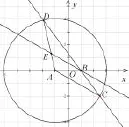
图1　

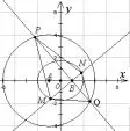
图2　

至于计算多边形的面积问题，一般情况下，没有直接的计算公式，通常将多边形进行割补，转化为求三角形面积问题.本题四边形是对角线互相垂直的四边形，其面积等于对角线长度之积的一半.只要知道这个公式，其计算方法和套路都是考生熟悉的.用一个参数表示四边形的面积，然后利用函数思想求四边形面积取值范围.如果设直线l的点斜式方程，就必须讨论直线l斜率不存在情形，此情形正是四边形面积取得最小值情况.

在试题设问上，命题专家充分考虑到考生的平面几何基础问题，给考生搭建台阶，逐步递进，首先证明|EB|+|EA|为定值，然后写出点E的轨迹方程，目的是启发引导考生思维方向.在某种程度上，有暗示考生利用定义法求轨迹方程，有利于考生顺利解答.若将试题的设问改为“求点E的轨迹方程”，试题难度会陡然上升，考生在解答时，首先必须对曲线的模型进行猜测，然后再选定解决问题的方法，利用定义法还是其它方法，对考生的要求就大大提高.

数学是研究空间形式和数量关系的一门学科，坐标法研究几何问题是解析几何的本质，其实质就是将问题中的几何要素用坐标或方程表示，利用坐标运算和方程思想，来研究几何图形的性质.虽然如此，但仍然注意图形的几何性质.新课标人教版教材中在旁白栏目明确指出，“适当利用图形的几何性质，有助于简化计算”.这种以“形”助“算”，以“数”解“形”，数形相依，相得益彰正是解析几何精髓所在.

二、试题溯源与拓展

1.教材习题与考题比较

本题源于人教版教材选修2-1中2.2节中习题.

如图3，圆O的半径为定长r，A是圆内一点（异于点O），P是圆上任意一点，线段AP的垂直平分线l和半径OP相交于点Q，当点P在圆上运动时，点Q的轨迹是什么？为什么？

教材习题利用线段的垂直平分线的性质构造等腰△QAP，且|QA|=|QP|，从而得到|QO|+|QA|=|OP|= r，根据椭圆的定义可知点Q轨迹是以点O、A为焦点，长轴长为r的椭圆.

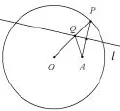
图3　

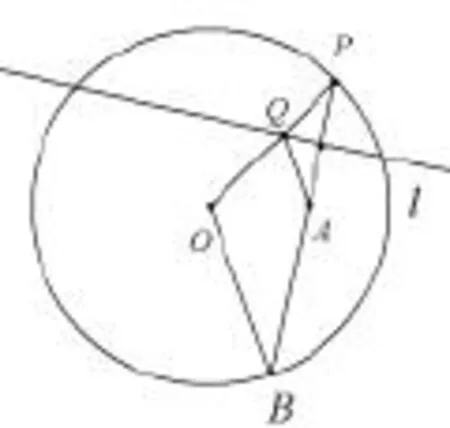
图4　

如图1，今年高考新课标I卷第20题是通过平行线的性质和圆的性质构造等腰△EBD，且|EB|=|ED|，从而得到|EB|+|EA|=|AD|.根据圆的方程和点B的坐标，可以进一步求点E的轨迹方程.

习题深究 如图4，对习题稍作加工改造，延长线段PA交圆O于点B，连接OB，由平面几何知识，可得∠P=∠B=∠QAP.所以QA//OB.线段AP的垂直平分线与半径OP交点，就是过点A作OB的平行线与半径OP的交点.从而发现，2016年高考新课I卷解答第20题是将课本的习题一般情形进行具体化而形成.

2.类比联想，从椭圆拓展到双曲线

我们可以将考题椭圆问题类比推广到双曲线中，可以得到类似的命题：

拓展1设圆x2+y2+ 8x=0的圆心为A，直线l过点B（4,0）且与x轴不重合，l交圆A于C，D两点，过B作AD的平行线交直线AC于点E.证明|EB|-|EA|为定值，并写出点E的轨迹方程（如图5）.

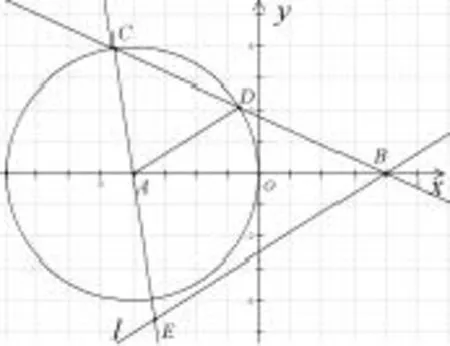
图5　

拓展2设圆x2+y2+ 8x=0的圆心为A，直线l过点B（4,0）且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交直线AD于点E.证明|EA|-|EB|为定值，并写出点E的轨迹方程（如图6）.

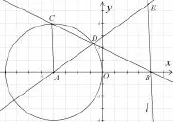
图6　

人教版教材选修2-1中2.3节有类似于2.2节的习题：如图7，圆O的半径为定长r，A是圆O外一点，P是圆上任意一点，线段AP的垂直平分线l和半径OP所在直线相交于点Q，当点P在圆上运动时，点Q的轨迹是什么？拓展1与2就是该题习题的变式.

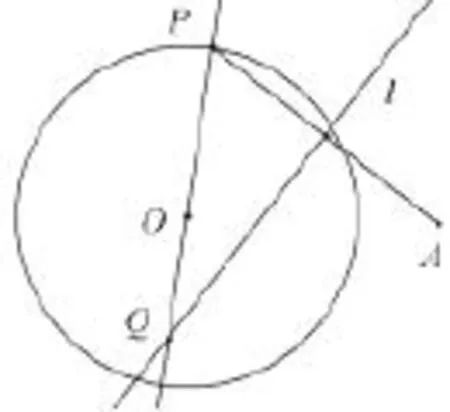
图7　

三、几点思考

1.注重知识间内在的联系，数学各知识间并不是完全独立的，而是有着天然的联系，这些联系也是高考试题设计的突破口.如函数与不等式、函数与方程、数列与函数、解析几何与函数、解析几何与平面几何等等.对于一道数学题来说，与之联系问题有很多，往往这种联系没有被发现，尤其是一些数学素养不高的学生，是不能发现这种联系的.如2016年高考新课标I卷第20题，将平面几何中圆知识、平行线知识、四边形面积公式、函数知识与解析几何知识有机联系在一起，注重考查考生综合运用所学知识分析问题、解决问题、逻辑推理和运算求解能力.因此，在日常教学中，要积极引导学生通过问题解决梳理知识间的联系，做到触类旁通，举一反三.正如数学家笛卡尔所说：“我们解决的每个问题都将成为一个范例用于解决其他问题.”

2.重视教材的蓝本作用，教材是实现课程标准的载体，是课堂教学的素材.教材是专家精心打造的，凝聚专家的智慧.特别是教材中例题和习题，是编写专家遴选的.因此，教师在日常教学中，应重视教材作用和地位，发挥教材的教学功能，能科学地开发教材，创造性地使用教材，善于对教材例题和习题，尤其一些典型例题和习题，进行重组变式和拓展.并让学生自己经历和感受改造教材中习题、提出新问题、解决新问题历程，培养学生创新意识.爱因斯坦就指出：“提出一个问题往往比解决一个问题更重要，因为解决一个问题也许只是一个数学上或实验上的技巧问题.而提出新的问题、新的可能性，从新的角度看旧问题，却需要创造性的想象力，而且标志着科学的真正的进步.”

3.强化表征能力培养，著名心理学家西蒙指出：“表征是问题解决的一个中心环节，它说明问题在头脑里是如何呈现的，如何表示出来的”.数学问题通常用符号语言、文字语言、图形与图表等表征出来的.对不同形式的表征，能有效转化，将抽象的问题具体化，复杂问题简单化，是解决数学问题关键.前面分析的高考试题，就充分体现一点，如何从题目中几何图形表征，提取信息，转化表征形式，发现问题本质，确立解题策略.因此，教师在教学中应注重发展学生数学语言转换能力，深化数学问题表征能力的培养.

总之，数学课堂教学不能急功近利，不能通过刷题、题海战术，来提高学生的解题能力.应通过夯实基础，注重联系，强化反思，培养能力，突出创新，不断积淀，来提升学生的数学素养.

［1］人民教育出版社.普通高中课程标准实验教科书数学［M］.人民教育出版社，2014.

［2］黄严生.抓住联系 突破思维障碍 实现有效转化［J］.中学数学教学，2015（3）：16-19.

［3］李艳华.数形结合思想在高中数学解题中的实践［J］.中学数学，2016（5上）：75-76.

［4］陈昂 任子朝.高考数学试题情境创新研究［J］.中学数学教学参考，2016（6上）：2-4.