一道高考解几压轴试题的赏析

福建省龙海第一中学新校区（363100）　苏艺伟



一道高考解几压轴试题的赏析

福建省龙海第一中学新校区（363100）苏艺伟

试题（2016年全国I卷理科第20题）设圆x2+y2+ 2x-15=0的圆心为A，直线l过点B（1,0）且与x轴不重合.l交圆A于C，D两点，过B作AC的平行线交AD于点E.

（1）证明|EA|+|EB|为定值，并写出点E的轨迹方程.

（2）设点E的轨迹为曲线C1，直线l交C1于M，N两点.过B且与l垂直的直线与圆A交于P，Q两点.求四边形MPNQ的面积的取值范围.

试题分析本道试题分为两步，第一步考查用定义法求轨迹方程，较为基础；第二步求对角线互相垂直的四边形面积取值范围，具有一定的难度.从知识层面讲，融合了直线，圆，椭圆等高中阶段重要的知识点，强调知识的融汇贯通，交叉渗透；从能力立意的角度讲，侧重考查考生通过一系列的思维过程：画图分析（全国卷的解几压轴试题一般不给出图形）—直观感知—操作确认—计算求解—推理论证，从而达到能力立意的高度，对考生的思维量，计算能力提出了较高的要求.从难易层面讲，两问具有梯度性，能够让不同的考生都有所收获，让优秀的学生得到更高的分数，具有区分度.可以说，本道试题延续了全国卷命题的一贯风格，既注重基础知识，又强调能力立意，不失为一道好题.

一.对第一步的赏析

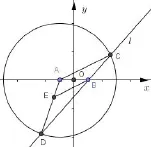
图1　

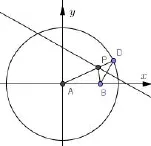
图2　

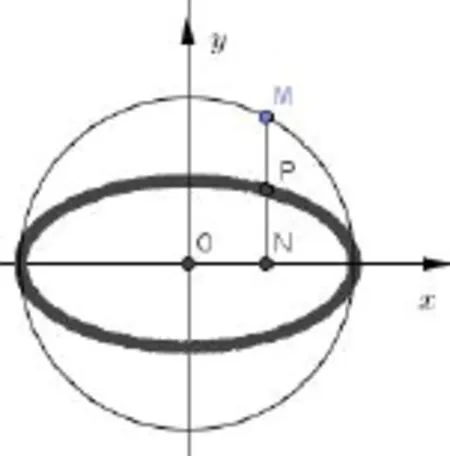
图3　

图4　

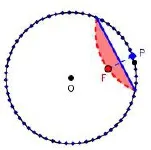
图5　

图6　

1.1解法

1.2赏析

该小步的本质是利用椭圆定义求出动点的轨迹方程.由于将背景设置在直线与圆当中，增加了试题的迷惑性，复杂性.考生要能够正确求解，必须建立在对图形的准确观察以及简单的推理论证基础之上，然后结合椭圆定义求出动点E的轨迹方程.众所周知，椭圆定义是高中阶段一个非常重要的内容，即动点P到两定点A，B的距离之和为定值（且该定值大于两定点的距离）的点的集合：｛P||PA|+|PB|=2a,2a＞|AB|｝.这是学生都非常熟悉的，但是在实际考试当中，试题往往不会直接给出这么明显的条件，而是经过一系列的包装（经常和圆结合，在圆中得到椭圆，本道试题其实给我们提供了一种从圆中得到椭圆的方法），这就要求我们要熟悉一些常见的从圆中得到椭圆的几何模型.

1.如图（2）所示，在平面直角坐标系中，任作一个圆A，在直径上任取一点B（该点在圆内）.然后在圆上取一点D，连接DA，DB.作出DB的垂直平分线交DA于点P，则当点D运动时，点P的轨迹为椭圆.

2.如图（3）所示，在平面直角坐标系中，在圆x2+y2= a2（a＞0）上任取一点M，做MN⊥x轴，垂足为N.取MN中点P，则当点M在圆上运动时，点P的轨迹为椭圆.

4.如图（5），（6）所示，一张纸上画有半径为R的圆O，F为圆内一定点.折叠纸片，使圆周上一点P刚好和F重合，这样的每一种折法，都会留下一条折痕.当点P取遍圆周上所有点时，折痕的轮廓线是以O，A为焦点的椭圆.

熟悉了上述几种几何模型，我们就能够站在一个更高的高度来重新审视该题，即透过表现看到本质，从圆中得到椭圆.总之，该小步的求解不仅需要对椭圆定义有一个全面的认识，还要求能够根据题目条件灵活运用，真正做到了缘于基础，又高于基础，突出考查学生的理性思维，逻辑思维，对高考备考具有很好的导向作用.

二.对第二步的赏析

2.1解法

解法1从直线的斜率入手.如图（7）所示，由于直线l过点B（1,0）且与x轴不重合，故可设直线l方程为x=my+1，则直线PQ的方程为y=-m（x-1）.

图7　

图8　

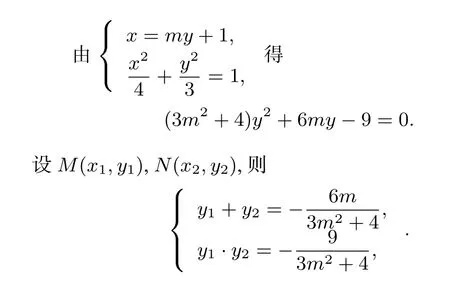
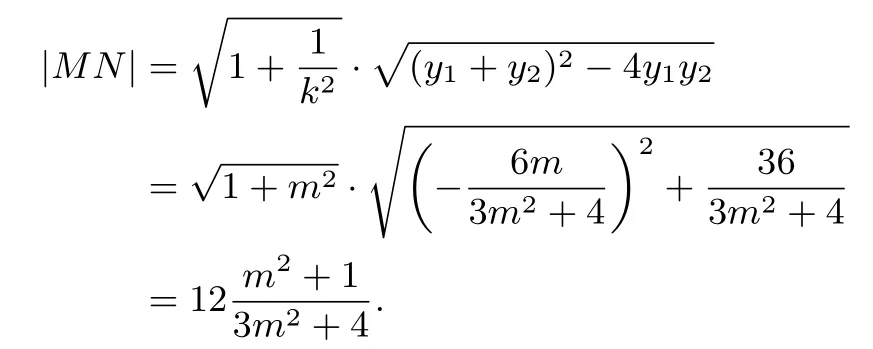
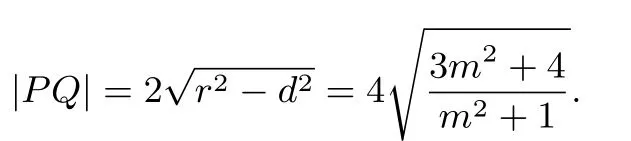
因此四边形MPNQ的面积

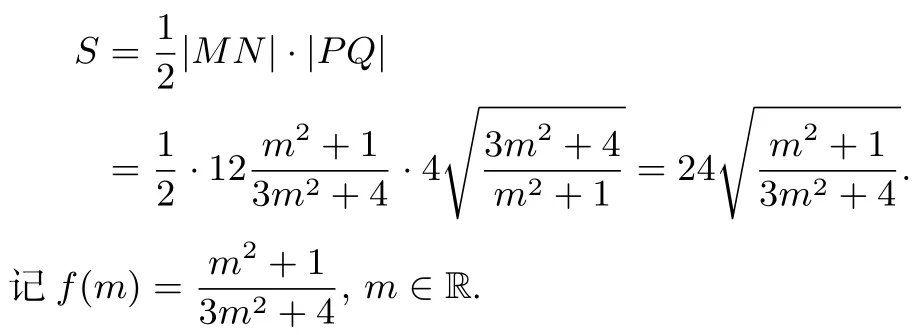
以下采用三种方法来求出f（m）的取值范围.

方法1：求导

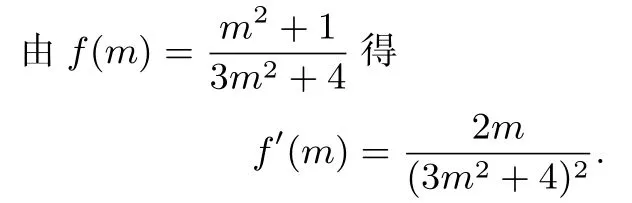
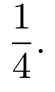
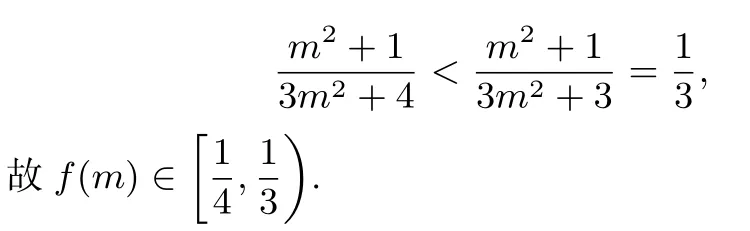
方法2：利用齐一次分式函数图象和性质

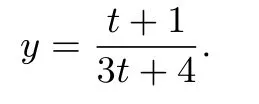
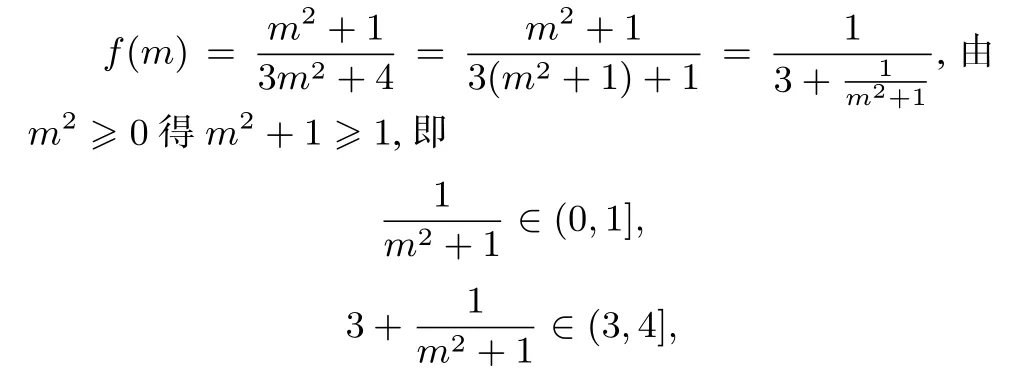
方法3：配凑

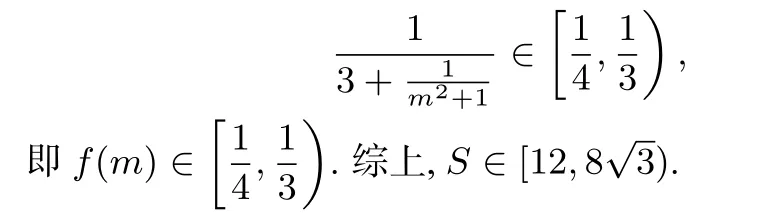
解法2从设角度入手.如图（7）所示，设∠MBA=θ，由于直线l与x轴不重合，故θ∈（0,π）.

在△MAB中，由余弦定理有

结合|MA|+|MB|=4可得

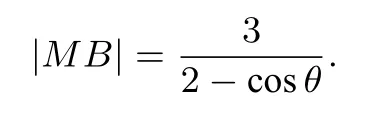
在△NAB中，由余弦定理有

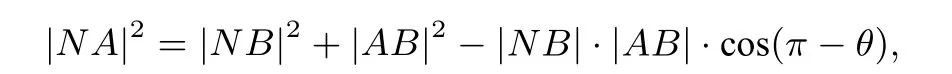
结合|NA|+|NB|=4可得

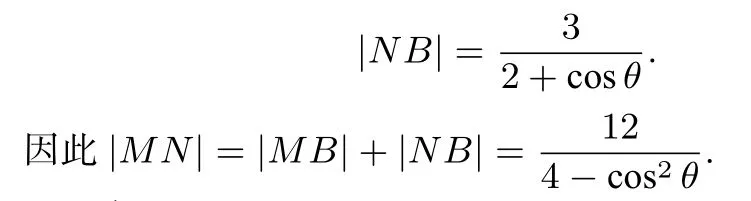
圆心A（-1,0）到直线PQ∶cosθ·x-sinθ·y-cosθ=0的距离为

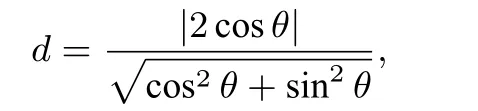
则

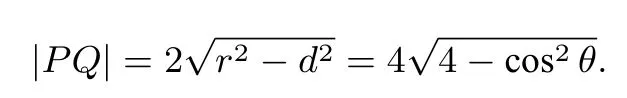
因此四边形MPNQ的面积

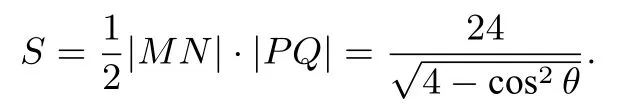
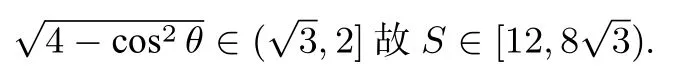
解法3从特殊情况入手.如图（9），（10）所示.

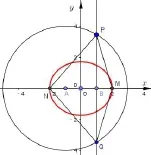
图9　

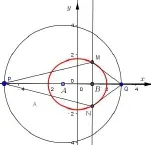
图10　

假设直线l与x轴垂直，此时直线PQ与x轴重合.则MN为椭圆的通径，|MN|=3，PQ为圆A的直径，|PQ|=8.

观察图形可知，当直线l绕着点B旋转时，四边形MPNQ的面积S介于这两种特殊情况之间.由于题目条件直线l与x轴不重合，故

2.2赏析

该小步涉及到三个基本图形：直线，圆，椭圆；四个基本点：M,P,N,Q（其中两个点在圆上，两个点在椭圆上）；一个四边形：四边形MPNQ.要求的是四边形MPNQ的面积的取值范围，前提条件是这个四边形的两条对角线互相垂直.涉及到的知识点有：点到直线的距离公式，圆中弦长公式，椭圆中弦长公式，对角线垂直的四边形面积公式，函数值域的求法等等.该小步解法多样，入口宽，着重突出考查考生的逻辑思维能力，推理论证能力，运算求解能力，凸显全国卷以能力立意的命题宗旨.

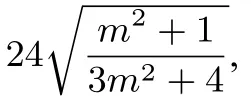
通过上述分析不难发现，本道试题的命制是建立在命题者对课本教材相关知识点挖掘的基础之上，然后进行一系列的融合，研磨.它与2013年全国I，II卷的圆锥曲线试题具有异曲同工之处.

2013年全国I卷理科第20题已知圆M ∶（x+1）2+ y2=1，圆N∶（x-1）2+y2=9，动圆P与圆M外切，并与圆N内切，圆心P的轨迹为曲线C.

（1）求C的方程；

（2）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|.

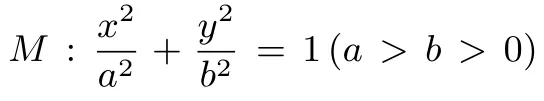
（1）求M的方程；

（2）C，D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值.

三.对本题的推广

设圆A的圆心为A（-c,0），半径为2a（0＜c＜a），直线l过点B（c,0）且与x轴不重合.l交圆A于C，D两点，过B作AC的平行线交AD于点E.则有

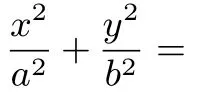
（2）设点E的轨迹为曲线C1，直线l交C1于M，N两点.过B且与l垂直的直线与圆A交于P，Q两点.则四边形MPNQ的面积S∈［4b2,4ab）.

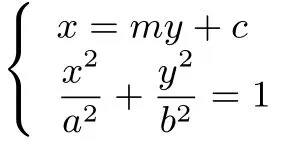
因此四边形MPNQ的面积

四.备考建议

1.重视对学生数学直觉的培养

史宁中教授这样阐述道：任何一门学科都应该把培养学科直觉作为一个根本的教育任务.数学要培养数学直观，数学的结论是看出来的，不是证出来的.因此培养数学直观是很重要的，而直观的培养是学生经验的积累，而不是老师说教的结果，所以要帮助学生培养基本活动经验.

对于本题第一步，直觉思维告诉我们，这是从圆中得到椭圆的一种方法.对于第二步，直觉思维提醒我们考虑特殊情况，进而得到面积的取值范围.由此可见，直觉思维在我们解题中发挥着至关重要的作用.

笔者认为，所有的定理只有在直觉理解，想通领悟的前提下才能被学生真正接受.基于此，在备考中要为学生创造更多的有意义的学习经历，以培养学生的数学直觉.笔者认为可以从以下两方面入手.第一：引导学生理解概念的形成过程，在身临其境中感悟概念，让学生不仅知其然，还能知其所以然，并能运用所学概念解决实际问题.第二：注重结论的推导过程，让学生运用所学知识推导新结论，提高学生的灵活运用能力与数学学习能力.

2.加强解题后反思，进一步发展思维和提升能力

南京师范大学的单墫教授认为，同一个数学问题的不同解法，可以有美丑之分，简洁明快是一种数学美.在数学解题教学中，要引导学生寻求更美的解题方法.应当引导学生加强解题后反思.思考同一道题目是否有更好的解法？思考问题可否进一步变换与引申，诸如题目条件不变，是否可以变换出新的结论；题目条件再加强一些，是否可以引申出新的结论等等.如此解题反思，对于调动解题积极性，培养发展思维，创造性品质有着重要的意义.