2016年全国高考乙卷（文理科）第19题分析及启示

广州市执信中学（510080） 刘诗顺

华南师范大学数学科学学院（510631）　苏洪雨



2016年全国高考乙卷（文理科）第19题分析及启示

广州市执信中学（510080） 刘诗顺

华南师范大学数学科学学院（510631）苏洪雨

一、题目

（理科）某公司计划购买2台机器，该种机器使用三年后即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元.在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：

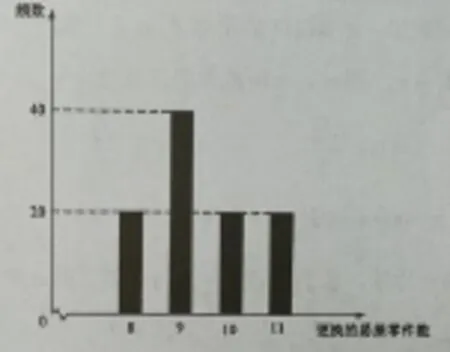
图1　

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记X表示2台机器三年内共需更换的易损零件数，n表示购买2台机器的同时购买的易损零件数.

（I）求X的分布列；

（II）若要求P（X≤n）≥0.5，确定n的最小值；

（III）以购买易损零件所需费用的期望值为决策依据，在n=19与n=20之中选其一，应选用哪个？

（文科）某公司计划购买1台机器，该种机器使用三年后即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元.在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：

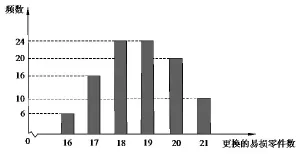
图2　

记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元），n表示购机的同时购买的易损零件数.

（I）若n=19，求y与x的函数解析式；

（II）若要求“需更换的易损零件数不大于n”的频率不小于0.5，求N的最小值；

（III）假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？

二、解答赏析

理科（1）由柱状图并以频率代替概率可得，一台机器在三年内需更换的易损零件数为8，9，10，11的概率分别为0.2,0.4,0.2,0.2.X的可能取值为：16,17,18,19,20,21,22，从而

P（X=16）=0.2×0.2=0.04；

P（X=17）=2×0.2×0.4=0.16；

P（X=18）=2×0.2×0.2+0.4×0.4=0.24；

P（X=19）=2×0.2×0.2+2×0.4×0.2=0.24；

P（X=20）=2×0.2×0.4+0.2×0.2=0.2；

P（X=21）=2×0.2×0.2=0.08；

P（X=22）=0.2×0.2=0.04.

所以X的分布列为

X 16 17 18 19 20 21 22 P 0.04 0.16 0.24 0.24 0.2 0.08 0.04

......................................................5分

（2）由（1）知P（X≤18）=0.04+0.16+0.24=0.44，P（X≤19）=0.04+0.16+0.24+0.24=0.68，故n的最小值为19...............................................8分

（3）记Y表示2台机器在购买易损零件上所需的费用（单位：元）.当n=19时，

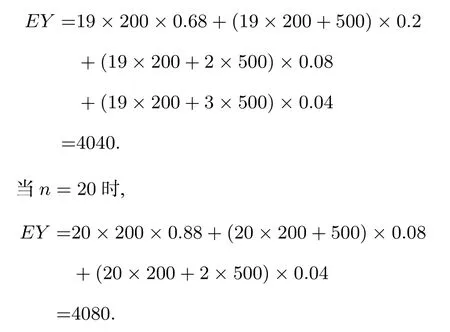
可知当n=19时所需费用的期望值小于n=20时所需费用的期望值，故应选n=19..........................12分

评析 在第（1）问中，柱状图反映的是100台机器三年内更换的易损零件数的频率，以此频率代替1台机器更换的易损零件数发生的概率，从而才能得到一台机器在三年内更换的易损零件数为8，9，10，11的概率，有些同学不能读懂题意而导致错误.2台机器三年内更换的易损零件数X的情况多达8种，平常练习中X的取值一般只有4-5种，故题目的难度一下子增大.

在第（2）问中，式子P（X≤n）≥0.5中两个字母，两个不等号，平常这种题训练较少，理解起来有一定的困难，就算理解了，但又不知道怎样用数据来说理.

在第（3）问中，题目要求是以购买易损零件所需费用的期望值为决策依据，而不是以易损零件数的个数X的期望值为依据，有些同学习惯性的直接求X的数学期望值而造成错误.另外两种解法供参考.

第三问方法一购买零件所需费用含两部分，一部分为购买机器时购买零件的费用，另一部分为备件不足时额外购买的费用.

当n=19时，所需费用的期望为：

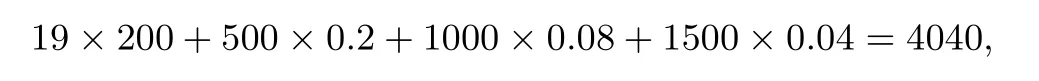
当n=20时，所需费用的期望为：

所以应选用n=19.

第三问方法二购买零件所需费用包括两部分，一部分为购买机器时购买零件的费用，另一部分为备件不足时额外购买的费用.

当n=19时，设所需费用为Y1，则随机变量Y1的分布列为

Y13800 5300 4300 4800 P 0.68 0.20 0.08 0.04

所以Y1的数学期望为：

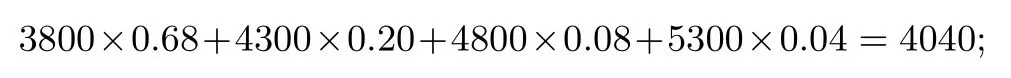
当n=20时，设所需费用为Y2，则随机变量Y2的分布列为

Y24000 4500 5000 P 0.88 0.08 0.04

所以Y2的数学期望为：

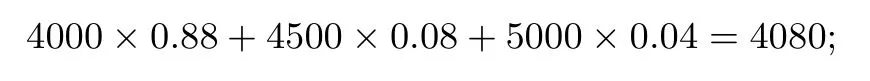
因为EY1＜EY2，所以应选用n=19.

文科（1）当x≤19时，y=3800.当x＞ 19时，y=3800+500（x-19）=500x-5700.所以y与x的函数解析式为：

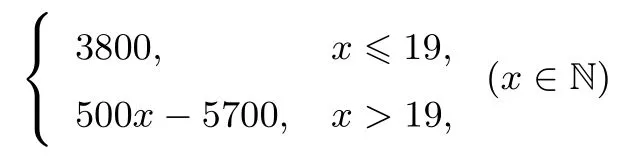
......................................................5分

（2）由柱状图知，需更换的零件数不大于18的频率为0.46，不大于19的频率为0.7，故n的最小值为19......8分

（3）若每台机器在购机同时都购买19个易损零件，则这100台机器中有70台在购买易损零件上的费用为3800，20台的费用为4300，10台的费用为4800，因此这100台机器在购买易损零件上所需费用的平均数为：

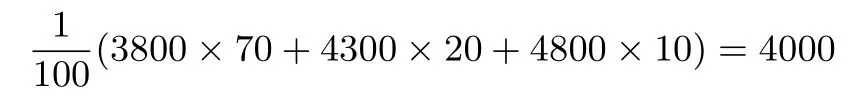
若每台机器在购机同时都购买20个易损零件，则这100台机器中有90台在购买易损零件上的费用为4000，10台的费用为4500，因此这100台机器在购买易损零件上所需费用的平均数为：

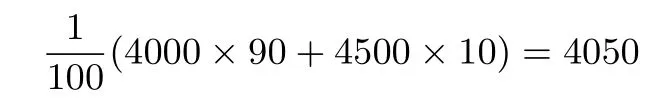
比较两个平均数可知，购买1台机器的同时应购买19个易损零件..............................................12分

评析 第（1）问，是一个分段函数，写出该分段函数难度不大，但是要特别注意其定义域.第（2）问，首先是这句话“‘需更换的易损零件数不大于n’的频率不小于0.5”，对一些“数学不太好，语文更糟糕”的考生来说，理解起来实属不易.只要理解了这句话，解答还是很简单的，给出下列几种解法供参考.

方法一（频率法）需更换的易损零件数不大于18的频率为0.06+0.16+0.24=0.46，需更换的易损零件数不大于19的频率为0.06+0.16+0.24+0.25=0.7，因为0.46＜0.5，0.7＞0.5，故应取n=19.

方法二（频数法）需更换的易损零件数不大于18的台数为6+16+24=46，需更换的易损零件数不大于19的台数为6+16+24+24=70，100×0.5=50（台），46＜50，70＞50，故n的最小值为19.

方法三（频率差数法）需更换的易损零件数不大于18的频率为0.06+0.16+0.24=0.46，0.5-0.46=0.04，因为0.04＜0.24，故n的最小值为19.

方法四（频数差数法）需更换的易损零件数不大于18的台数为6+16+24=46，50-46=4，因为4≤24，故N的最小值为19.

第（3）问，题目要求是以100台机器在购买易损零件上所需费用的平均数作为决策依据.

三、答卷的主要错误分析

有关考试的主要错误及原因，请参见本期的另文：

刘秀湘，2016年高考数学广东卷试题和答卷分析，中学数学研究［J］，2016，9（上半月刊）.

四、对2017年高考概率统计备考及中学教学的几点启示

针对2016年全国高考乙卷第19题出现的主要问题，对概率统计模块的备考和教学提出以下建议：

首先：重视基本概念的教学，尤其是概念本质的理解.《普通高中数学课程标准（实验）》指出：“数学教学中应强调对基本概念和基本思想的理解和掌握，对一些核心的概念和基本思想要贯穿高中数学教学的始终，帮助学生逐步理解.由于数学高度抽象的特点，注意体现基本概念的来龙去脉，在教学中要引导学生经历具体实例抽象数学概念的过程，在初步运用中逐步理解概念的本质.”数学概念是数学的逻辑起点，是学生认知的基础，是学生进行数学思维的核心.而考卷上的概念一般都源自教材，在复习备考和教学中，要引导学生对教材中的基本概念、易错易混淆概念进行辨析理解，充分挖掘概念的内涵与外延.例如本题中的频率与概率.频率是实验中某一事件发生的次数与实验总次数之比.频率会随着实验条件的改变而变化.概率是频率的稳定值，是客观存在的一个数，是对总体而言的.再例如柱状图的概念，“排列数”与“组合数”的理解和区分等.

其次：重视思想方法的教学，尤其是核心素养的培养.新的一轮课程改革即将开始，而这一轮课改将以核心素养立意，数学学科的核心素养有：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析.今年的数学试卷体现了数学在解决实际问题的应用价值，体现了课程改革中加强应用性、实践性的特点.尤其是本题，题目长，难度大，以能力立意，考查数学的基本思想，在新课程理念上体现了数学抽象、数学建模、数据分析等核心素养.从本题解答的情况来看，考生“惧于抽象推理，烦于建模应用”，本质上是数学思想方法内化不够，数学抽象能力不足，数学建模意识不强.在备考和教学中应注重数学思想方法的渗透，注重核心素养的培养，尤其是数学抽象和数学建模能力的培养.例如：二项分布与超几何分布是随机现象中两种最基本的离散型随机变量服从的分布，是高考的常考考点.在教学中，应该通过具体的例题，让学生真切体会二项分布与超几何分布的异同点，培养学生抽象数学问题和准确识别概率分布模型的能力.

第三：重视语言表述的规范性，尤其是解题格式的训练.概率统计题一般是一个实际应用性质的题，解答通常需要先将实际问题抽象简化为数学模型，然后对数学模型进行分析求解，得到数学结论，再将数学结论进行验证并回答实际问题.中间穿插着自然语言与数学语言的转化互译，要注意数学语言中的“文字、符号、图形”之间的转换，做到文字要准确，符号要规范，逻辑要清晰.教师在平时的教学中板书要规范，表述要严谨.例如今年理科第19题在求离散型随机变量的分布列时，先要写出随机变量的所有可能取值，再求出随机变量的每一种取值对应的概率，并且要列式写出过程，最后列表写出随机变量X的分布列，并检验各列的概率之和是否等于1.平常如果按照以上规范步骤作答，将书写要点写出来，并辅以相应的文字说明，那么将会有效提高概率统计题的得分率.

第四：重视运算能力的培养，尤其是良好习惯的养成.《普通高中数学课程标准（实验）》明确指出：要提高学生的运算求解的能力.加强运算能力培养，这是一个整体的要求.其实不仅仅是概率统计模块，其他模块也有因计算错误失分的现象.因计算错误失分看似偶然，其实是平时的问题.在计算时候尽可能用笔算.某些考生口算不熟练，还要“耍小聪明”而造成计算失误.良好的计算习惯包括认真审题的习惯、认真细致计算的习惯、验算的习惯、良好书写的习惯等.养成良好的计算习惯，功夫要下在平时，平常的教学中要对学生提出要求，使他们明白应该怎么做，对做得好的要及时表扬，不好的要及时指出更正，同时教师在平常的教学中要以身作则起好示范作用.