基于混合算法求解ELSP问题的可行域分析

2016-10-24邱深山

华南师范大学学报（自然科学版） 2016年4期

张　琴, 邱深山，谢　中, 王　琦

(1.广东技术师范学院电子与信息学院，广州 510665；2.广州天河科技园管委会，企业博士后科研工作站，广州 510663；3.广州天河科技园管委会，广州 510663；4.广东工业大学应用数学学院，广州 510006)

张琴1*, 邱深山2，谢中3, 王琦4

给出了求解ELSP问题(EconomicLotSchedulingProblem)的可行域的特征、启发式规则和演化神经网络设计问题. 经济批量问题采用基本时段方法表示，该方法产生2类决策变量：表示基本时间段的连续变量和表示时间倍数的整数变量. 在求解ELSP问题的算法设计中，可行域是判定启发式规则有效性的基础. 为了给出可行域的特征，利用神经网络的演化计算，给出了求ELSP问题的初值算法，设计演化参数函数、网络结构、演化函数、演化规则，并依此获得可行域的约束条件. 对在可行域约束条件和启发式规则下设计的算法进行测试，并与用HGA和一般GA方法求解ELSP问题进行比较，求解效率明显提高，使得在满足可行性的前提下总费用减小.

经济批量问题；演化神经网络；遗传算法；混合算法；可行域

Keywords：ELSP(EconomicLotSchedulingProblem);recurrentneuralnetwork;geneticalgorithms;hybridalgorithms;thefeasibledomain

经济批量问题(EconomicLotSchedulingProlbem,简称ELSP)已被证明是一个NP难题[1],为求得其近似最优解，研究者们提出了很多精简的分析方法和启发式算法，如应用迭代算法、遗传算法、分支定界算法和整数规划等方法获得了一系列局部最优解[2-8]，考虑调整时间依赖于生产顺序问题[3]，应用模拟退火方法、邻域搜索算法、神经网络方法得到了局部最优解[8-11]，也有以较大规模数据为基础给出了全局最优解的算法[12]．多数研究者以具体实例得到全局最优解，但绝大多数是概率意义上的最优解，在未获得解析解前，给出求全局最优解的一般方法非常困难．

文献[13-16]虽研究了全局最优解的一般方法，但未考虑设备共享和有限产能的限制，为此，BOMBERGER[17]提出了能力约束条件，改进了求解ELSP问题模型，利用基本时段(简称BP)方法给出一种动态规划方法(简称DP). 虽然文献[18]在文献[19]的基础上提出了能够确定最优解范围的启发式方法，但由于没有给出ELSP问题的特点与初始值之间的依赖关系，在保证可行性方面计算效率不高[3,8,20-21]. 分析其原因是启发式规则设计的算法缺乏对可行域刻画和对参数初始化的优化.

本文提出基本时段问题的初始值优化计算方法，刻画了可行域，把启发规则嵌入到算法设计中，用演化神经网络算法配合遗传算法对ELSP问题进行求解.

1　问题描述和可行域

1.1问题描述

ELSP问题描述为一个单一的设备或者生产线可以生产多种不同的产品，每种产品的生产速度和需求速度已知，设备每次只能生产一种产品. 当转换为生产另一种产品时要花费一定的成本和时间，需要进行合理的排产，以在满足产品需求的基础上使得库存费用和调整费用之和最小.

传统ELSP问题的假设条件见文献[17]778，其中的参数定义见文献[22]588.

一种可行的排产方案定义如下[14]988:(1)一个生产周期的产品生产量足够满足这个周期的需求；(2)生产周期长度足够长使得所有产品都能在这个周期中生产.

ELSP问题的解是集合Γ={T1,T2,…,Tn},其中Ti必须足够长，以保证产品i的生产满足在周期Ti中的需求,同时剩下的时间(从产品i生产结束到下一个周期的开始)可以满足其他产品的生产. 可行性定义如下：如果集合Γ是可行的,而且使得总费用最小,则得到的解是ELSP问题的可行解.

单位时间产品i的平均费用定义如下：

所有产品的总费用为：

(1)

由此可见，ELSP的目标是找到一个满足可行性条件的集合Γ,使得TC最小.

1.2可行性条件

到目前为止，关于ELSP问题还未能给出一个封闭形式的解析解，其主要原因在于可行性条件难以验证. 非可行解表现为如下2种情况[22]588：

(1)生产能力非可行性：生产的负载超过了设备的能力；

(2)顺序非可行性(生产顺序冲突)：一个产品生产的开始时间比前一个产品生产完成的时间早.

本文只讨论生产能力的可行性，其条件为：

(2)

条件(2)保证用在生产产品和设备调整的时间不会超过可用时间，与目标函数(1)结合就是本文研究的主要问题.

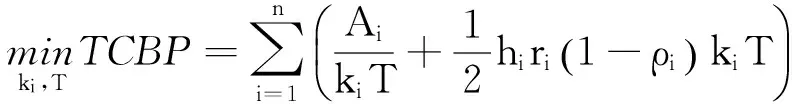
(3)

(4)

1.3可行域

本文的可行域是基本时段方法的可行域Ω：计算模型(3)、(4)的参数T和ki(i{1,2,…,n})满足条件(4)的区域Ω，即{k1,k2,…,kn,T}Ω．一般来说，这个区域Ω是在n+1维空间的满足可行性条件的区域. 我们分析得到可行性域中分量之间存在制约关系，这些制约关系是设计算法和启发式策略的主要依据，是判定启发式策略有效性的理论基础.

2　可行域分析与算法设计

2.1演化计算

演化计算是演化神经网络通过激活神经元的状态使得目标函数(1)趋于稳定的计算方法，稳定点就是局部极值点．本文研究将演化计算应用到初值优化计算上．基本时段模型假定每种产品都有特定的生产周期，每种产品i的周期Ti都是某个基本时段的整数倍，即Ti=kiT，T为基本时段,总的生产周期就是所有ki的最小公倍数乘以T值. 该方法的计算模型为：

(5)

本文算法设计目标是求模型(3)、(4)的最小值，以模型(5)的演化结果作为T和ki的初始化值．运用演化神经网络计算原理(有时也称之为迭代神经网络)[8]790，即以2个连续时刻演化值不同的神经元i进行演化为优先选择原则，然后再随机选择其他神经元. 从而避免采用随机选择初始值进行演化而产生远离可行域、稳定状态将落入局部极小点的情况，提高计算效率. 为此，将模型(3)、(4)转化为模型(5)，通过演化神经网络计算其初始值．

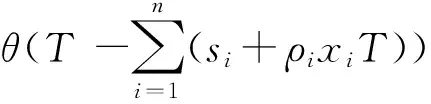
(6)也被称为能量函数[8]790，其极小值解就是模型(3)、(4)的1个解.

神经元i的演化规则定义如下：

xi(l+1)=fi(K,l)(l≥1),

(7)

2.2可行域与启发式规则

如果条件(4)成立，保证基本时段T足够长,则可以安排所有产品生产. 虽然基本时段方法获得的解优于CC方法，即共周期法[15]158,但是它难以保证收敛到可行解. 由于ki必须是正整数以及模型的复杂性，求解很困难,即使求得了T和ki的值,也不一定得到可行的排产方式. BOMBERGER[17]指出上述问题可以用动态规划方法求解，即固定T,通过求解动态规划问题找到最优的ki,然后利用已知信息来估计T. 因此，这个过程需要求解动态规划问题来找到最优的T,即该方法需要对T进行一维搜索. 为了研究方便，给出如下引理.

引理1[11]483可行解问题

min(x1,x2,…,xn,T)(n×+)∩ΩE(x1,x2,…,xn,T,θ)

的一个解是模型(3)、(4)的一个可行解.

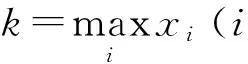
证明由于T满足:

(8)

则

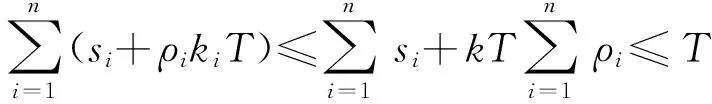
(9)

或者

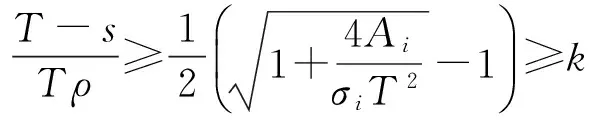
(10)

证明考虑式(9)左边作为变量T的不等式：

(11)

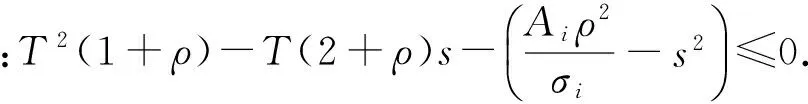
(12)

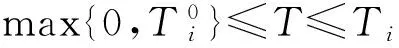
引理4证明类似引理3,在此略.

证明将式(7)代入罚函数(6),易知

E(x1,x2,…，xi(l)，…,xn,T,θ)-

E(x1,x2,…，xi(l+1),…,xn,T,θ)≤0，

其中xi(l+1)=fi(K，l).

引理7[2]358如果TUB和ki=1(i=1,…,n)不满足可行性条件,则对于任何的T和ki≥1(i=1,…,n)都不满足可行性条件.

该引理是用1个边界条件来判断1个区域上的结果.

在设计基本时段算法时，启发式规则的作用表现为当出现不满足可行性条件时，用二分法来确定满足条件的T′和ki(i=1,…,n). 这个启发式规则在算法设计中起到重要作用.

引理9[20]1317如果T和ki(i=1,…,n)满足可行性条件，那么存在一个δ，使得当T和δ满足：

1)δ>0,T，其中，；

则{ki,T+δ}满足可行性条件,且TC(ki,T)≥TC(ki,T+δ).

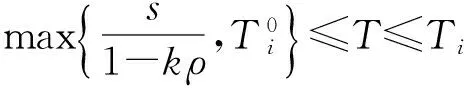
证明考虑在规则(7)下，选择第i(i{1,2,…,n})个神经元进行演化，即xi(l+1)=fi(K,l)下的函数变化：ΔE(xi(l))=E(x1,x2,…,xi(l+1),…,xn,T,θ)-E(x1,x2,…,xi(l),…,xn,T,θ),所以

当满足引理3的条件时，可以得到在规则(7)下,函数E(x1,x2,…,xn,T,θ)是递减的. 当演化遍历所有神经元时，局部极小值点存在. 再根据罚函数法可以得到模型(3)、(4)的局部极小值.

在对ELSP问题求解时，若利用率>88%，则运用基本遗传算法找到可行解的概率很低，此时因可行性区间非常小，随机选择初始值时很难落到该区域[3,20]. 为了提高找到可行解的效率，本文利用神经网络演化计算和启发式策略提出了一种高效搜寻可行解的方法；在利用率≤88%运用遗传算法时，虽然能找到可行解，但也容易陷入局部极小点. 针对这种情况，应用引理8，使得其算法能找到更小的目标值(即总费用更小).

在考虑给定的参数T和ki(i=1,…,n)下，在算法设计上分别使用演化神经网络方法和启发式规则来计算初始化初值和确定初始参数，本算法采用改进的启发式规则[2,20].

2.3算法设计

ki和T的初始值通过演化神经网络进行计算，当出现局部极小值时可利用引理7～引理9来调整，从而大大降低T的搜索空间，测试规模从1013降低到349. 实际测试表明，在此基础上确定初始值ki，再利用神经网络进行演化，明显提高求解ELSP问题的算法效率.

用神经网络计算的局部极值点作为模型(3)、(4)的初始化值，采用启发规则和初值选择来找到遗传算法的更好的局部最优解，搜寻最优解(次最优)的效率有很大提高.

通过定理1给出神经网络算法的局部最优解，以局部最优解作为初始值后再利用如下遗传算法进行求解，两者的优势结合可提高寻找最优解的计算效率. 算法设计步骤如下:

Step 1.依据演化神经网络算法给出的局部最优的初始值作为初始化GA初始值和参数(一般取ki=1(i{1,2,…,n}),TUB充分大[20,22])；

Step 2.产生初始种群，随机生成染色体中表示基本时间段的部分，将表示ki的部分由神经网络计算的局部最小结果给出；

Step 3.generation++(generation是遗传算法的代数的变量[20])，对当前种群运用随机联赛选择，交叉，均匀变异算子产生新的种群；

Step 4.如果当前最佳个体不满足可行性条件，则执行(i)(否则转Step 5)：

(i)判断TUB和ki(i{1,2,…,n})是否满足可行性条件，如果满足转(ii)，否则转(iii)；

(iii)转Step 2；

Step 5.如果连续100代最佳个体都未改变而且generation<=500，则执行如下：

(i)generation++，产生新种群，随机生成染色体中表示基本时间段的部分，表示ki的部分不变；

(ii)如果当前最佳个体的基本时间周期T>P/T，则此时T的取值范围设置为(P/T,T),否则,T的取值范围设置为(T,P/T).

(iii)按照此时T和k的范围计算适应度的值，对此时的个体进行评价.

Step 6.判断generation是否满足终止条件(到达最大代数1 000代，或者连续150代最佳个体都未改变)，如果满足，则算法结束，记录最佳个体的k值和T值，否则转Step 3.

3　算法的比较

在解决ELSP问题的过程中，求解目标不仅是总费用达到最小，而且要保证解的可行性条件. 一般利用遗传算法求解ELSP问题，需要5个部分：(1)问题的编码方案(附加初值进行优化方案)；(2)评价函数；(3)初始群体；(4)遗传算子；(5)运行参数. 在利用基本遗传算法求解的实验当中，我们发现该算法很容易在前几十代的迭代中就收敛到1个解，此时的这个解有2种情况：(1)是可行解，但非最优解；(2)不是可行解.

为了说明初值的优化和可行域的应用效果，将本文算法(简记为HIGA算法)应用到Bomberger标准问题中,并在利用率分别为88%和66%时与其他算法进行比较.

为便于比较分析，以Bomberger问题的标准数据(利用率为88%)[17]783作为比较标准值. 由表1和表2的运行结果可以看出，HIGA方法有更好的求解效率：在利用率为88%时，HIGA方法得到最优解的平均进化代数为89代，而GA方法平均进化代数为402代、HGA方法得到最优解的平均进化代数为178代；在利用率为66%时，HIGA方法得到最优解的平均进化代数为231代，而HGA方法得到最优解的平均进化代数为500代、GA方法平均进化代数为520代. 由此可见，初始化直接影响GA算法运行效率.

表1　HIGA、GA[3]和HGA[20]的参数对比表(利用率=88%)

表2　HIGA、GA[3]和HGA[20]的参数对比表(利用率=66%)

4　小结与展望

本文考虑基本时段(BP)方法的ELSP问题求解, 用分析方法刻画可行域. 在文献[3]、[10]的基础上，利用演化神经网络对ELSP问题的初始参数进行预处理，为启发式规则作用和效率提供理论支持，得到优化的排产方案，提高计算效率. 所得结果包括：

(1)利用演化神经网络作为计算初值框架给出了基于基本时段(BP)的可行域的内在关系、设计了演化函数、演化规则,证明了计算模型(3)、(4)与罚函数的关系.

(2)用ESLP基本时段问题的内在关系精细刻画可行域，提高GA算法计算效率.

(3)设计了跳出局部极小问题的启发式规则.

(4)当最佳个体不满足可行性条件时，利用引理7进行判断：判断当基本时间周期等于TUB时,TUB和ki(i)是否满足可行性条件. 如果不满足，则此时必须改变ki值才有可能找到可行解. 否则利用引理8寻找可行解的启发式策略，重新设置满足可行性条件时T的取值范围，然后再按照遗传算法继续演化. 在利用率很高的时候，该方法作用明显. 当利用率达到95%以上时，可猜测其就是全局最优解.

(5)如果当前最佳个体满足可行性条件，利用引理3寻找更小费用的启发式策略，改变T的取值范围，跳出局部最优，尽快找到更好的解.

(6)本文方法比GA方法、HGA方法有更好的求解效率.

本文设计的方法尽管是依据具体问题，但其设计思想具有一般性，主要表现在利用演化神经网络计算的优点进行遗传算法初值的计算. 因为初值的选择如果不适当，无论方法如何即便是给出了一个解，也未必是局部最优，是局部最优也无法到达全局最优，许多实际问题对初值是高度敏感的. 同时，本方法还可以推广到更一般的情况.

[1]HSU W L. On the general feasibility of scheduling lot sizes for several products on one machine[J]. Management Science, 1983, 29(1):93-105.

[2]GRZNAR J, RIGGLE C. An optimal algorithm for the basic period approach to the economic lot scheduling problem[J]. Omega-International Journal of Management Science, 1997, 23(3):355-364.

[3]KHOUJA M, MICHALEWICZ Z, WILMOT M. The use of genetic algorithm to solve the economic lot scheduling problem[J]. European Journal of Operational Research, 1998,110(3):509-524.

[4]YAO M J,ELMAGHRAPHY S E. The economic lot scheduling problem under power-of-two policy[J]. Computers and Mathematics with Applications, 2001, 41(10/11):1379-1393.

[5]SOMAN C A. A basic period approach to the economic lot scheduling problem with shelf life considerations[J]. International Journal of Production Research, 2004, 42(8):1677-1689.

[6]COOKE D L. Finding effective schedules for the economic lot scheduling problem:a simple mixed integer programming approach[J]. International Journal of Production Research, 2004, 42(1):21-36.

[7]DOBSON G. The economic lot-scheduling problem:achieving feasibility using time-varying lot sizes[J]. Operations Research, 1987, 35(5):764-771.

[8]QIU S S,TSANG E C C,YEUNG D S,et al.A general updating rule for discrete hopfield-type neural network with time-delay[C]∥Proceedings of the 17th international joint conference on Artificial intelligence.San Francisco:Morgan Kaufmann,2001:789-794.

[9]DOLL C L, WHYBARK D C. An iterative procedure for the single machine multi-product lot scheduling problem[J]. Management Science, 1973, 20(1):50-55.

[10]HUANG J YEN, YAO M J. A genetic algorithm for solving the economic lot scheduling problem in flow shops[J]. International Journal of Production Research, 2008, 46(14):3737-3761.

[11]陈宝林. 最优化理论与算法[M].北京:清华大学出版社,2005.

[12]MOON I K, SILVER E A. Hybrid genetic algorithm for the economic lot-scheduling problem[J]. International Journal of Production Research, 2002, 40(4):809-824.

[13]ROGERS J. A computational approach to the economic lot scheduling problem[J]. Management Science, 1958, 4(3):264-191.

[14]DAVIS S G.Scheduling economic lot size (ELS) production runs[J].Management Science,1990,36:985-998.

[15]HANSSMANN F.Operations research in production and inventory control[M]. New York:Wiley, 1962:158-160.[16]MAXWELL W. The scheduling of economic lot sizes[J]. Naval Research Logistics Quarterly, 1964, 11:89-124.

[17]BOMBERGER E. A dynamic programming approach to a lot size scheduling problem[J]. Management Science, 1966, 12(11):778-784.

[18]WAGNER B J, DAVIS D J. A search heuristic for the sequence-dependent economic lot scheduling[J]. European Journal of Operational Research, 2002, 141:133-146.

[19]MOON I K, HAHM J H, LEE C. The effect of the stabilization period on the economic lot scheduling problem[J]. IIE Transactions, 1998, 30(11):1009-1017.

[20]QIU X, CHANG H Y. A hybrid genetic algorithm for solving the economic lot scheduling problem(ELSP) [C]∥Proceedings of the Eighth International Conference on Machine Learning and Cybernetics.Baoding:IEEE, 2009:1315-1320.

[21]JENSEN M T, KHOUJA M.An optimal polynomial time algorithm for the common cycle economic lot and delivery scheduling problem[J].European Journal of Operational Research, 2004,156 (2):305-311.

[22]ELMAGHRAPHY S E. The economic lot scheduling problem(ELSP):review and extensions[J]. Management Science, 1978, 24(6):587-598.

【中文责编：庄晓琼英文责编：肖菁】

Analysis of the Feasible Domain of ELSP Problems Based on Hybrid Algorithms

ZHANGQin1*,QIUShenshan2,XIEZhong3,WANGQi4

(1.SchoolofElectronicandInformation,GuangdongPolytechnicNormalUniversity,Guangzhou510655,China；2.PostDoctoralResearchWorkstation，AdministrativeCommissionofGuangzhouTianheSoftwarePark，Guangzhou510663,China；3.AdministrativeCommissionofGuangzhouTianheSoftwarePark，Guangzhou510663,China；>4.SchoolofAppliedMathematics,GuangdongUniversityofTechnology,Guangzhou510006,China)

Theanalysischaracteristicsoffindingfeasiblesolutiondomain,heuristicstrategiesandalgorithmofRecurrentNN(NeuralNetwork)fortheEconomicLotSchedulingProblem(ELSP)problemsareproposed，whichcanbedescribedinbasictimemethod.Thismethodproducestwokindsofdecisionvariables,oneisthecontinuousvariablesforthebasicperiodoftime,andtheotheristheintegervariablesforthemultipleoftime.InthedesignphaseofthealgorithmforsolvingtheELSPproblem,thecharacteristicinformationofthefeasibledomaindeterminestheeffectivenessoftheheuristicstrategies.InordertosolveELSPproblems,itmustberequiredaneffectivetheheuristicstrategies.Theresearchresultsshowthatthecharacteristicsoffeasiblesolutiondomainimprovetheeffectivenessoftheheuristicstrategies.Basedontheadvantagesofevolutioncomputingofneuralnetwork,thealgorithmsforsolvinginitialvaluesofESLPproblemaredesigned,whichincludesevolvingfunction,networkstructure,evolutionfunctionandstrategies,sothattheconstrainedconditionsoffeasiblesolutiondomainisgiven.ThealgorithmsemployedfeasibledomainconditionsandheuristicstrategiesaretestedandcomparedwithHGAandtraditonalGAmethodsforsolvingESLPproblem.Thetestresultsshowthattheefficiencyofcomputingissignificantlyimprovedandthetotalcostdecreases.

2016-03-05《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(11201084)；广东省自然科学基金项目(s2012010008437)

张琴，工程师，Email: 573749120@qq.com.

TP18

1000-5463(2016)04-0125-07