广义指数分布顺序统计量的分布性质

李　娟，范梓淼，周菊玲

（新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017）

广义指数分布顺序统计量的分布性质

李娟，范梓淼，周菊玲*

（新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017）

文章在总体服从广义指数分布时，抽取样本X1，X2…，Xn，设X（1），X（2），…，X（n）为其顺序统计量，研究了（X（1），X（2），…，X（n））的联合概率密度函数；X（1）和X（n）的密度函数。进而得到了X（1）和X（n）的数学期望和方差，证明X（1），X（2）-X（1），…，X（n）-X（n-1）不独立且不同分布。

广义指数分布；顺序统计量；数学期望；方差

顺序统计量是概率统计中一类很重要的随机变量，它的分布在随机过程特别是泊松过程和数理统计中都有着诸多的应用。本文运用下面的原理构成理论基础：设n个电路元件的工作寿命为X1，X2，…，Xn。若将它们组成一个串联系统，且系统能正常工作当且仅当n个元件均正常工作，于是该系统能正常工作的寿命为若将它们组成一个并联系统，且系统能正常工作当且仅当至少有一个元件正常工作，于是该系统能正常工作的寿命为由于GE（广义指数分布）对于偏斜的寿命数据有很好的分析效果，而且还可以作为Gamma分布和Weibull分布的替代分布，因而在寿命试验和可靠性工程中有着重要的应用，也是统计学家和实际工作者十分关心的一个问题，因此对广义指数分布的研究有着十分重要的实际意义［15］。文章考虑广义指数分布：当Xk服从参数为θ和λ的广义指数分布，其中θ（θ＞0）为形状参数，λ（λ＞0）为尺度参数，即广义指数分布的密度函数和分布函数分别为

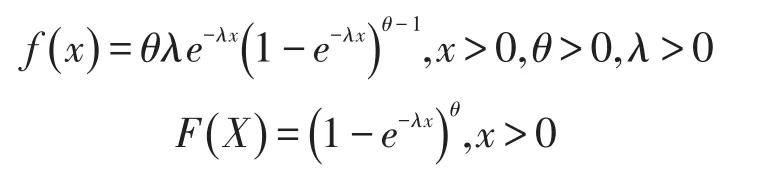
条件下顺序统计量的分布性质。

引理1［16-18］：设｛Xk:1≤k≤n｝独立同分布，有相同的分布函数F（x）和密度函数f（x），X（1），X（2），…，X（n）为其顺序统计量，则

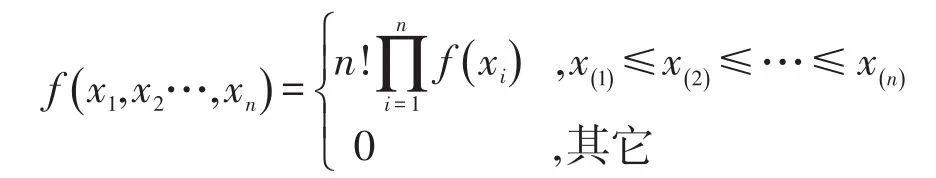
（2）X（k）的密度函数为

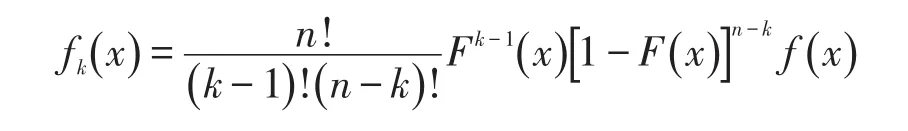
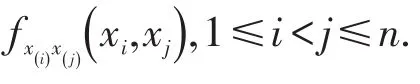
1　主要结果及结论

定理1：设｛Xk: 1≤k≤n｝独立同分布，Xk服从参数为θ（θ＞0）和λ（λ＞0）的广义指数分布，则：

（1）（X（1），X（2），…，X（n））的联合概率密度函数为

（2）X（1）的密度函数为

（3）X（n）的密度函数为

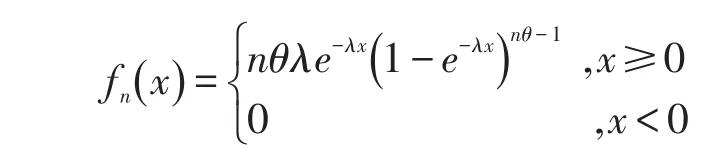
证明：由引理1及广义指数分布的密度函数与分布函数可得。

注：X（n）=max｛X1，X2…，Xn｝仍然服从两参数分别为nθ和λ的广义指数分布。X（1）=｛X1，X2…，Xn｝不服从广义指数分布，但是其概率密度函数可表示为n个不同的广义指数分布密度函数的线性组合。事实上，其概率密度函数的非零部分为

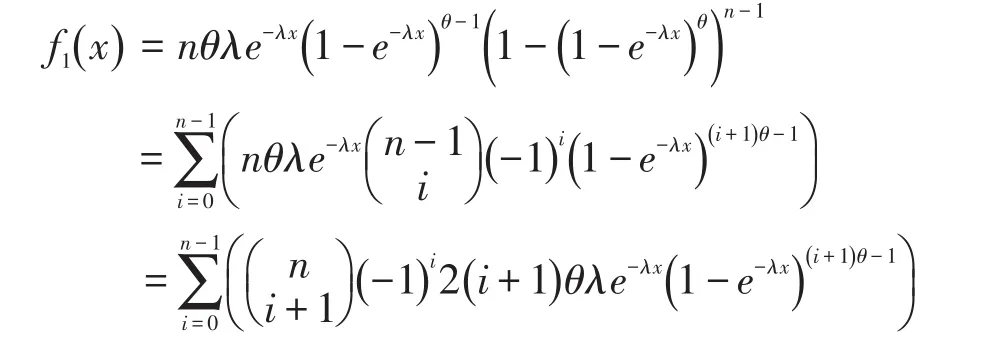
其中上式第二个等号是由二项式系数性质得到的。由此可见，f1（x）概率密度函数可表示为两参数分别为（i+1） θ（0≤i≤n-1）和λ的n个不同广义指数分布密度函数的线性组合。

定理2：设｛Xk: 1≤k≤n｝相互独立同分布，且Xk服从两参数分别为θ（θ＞0）和λ（λ＞0）的广义指数分布，X（1）=｛X1X，2…，Xn｝，X（n）=max｛X1，X2…，Xn｝则

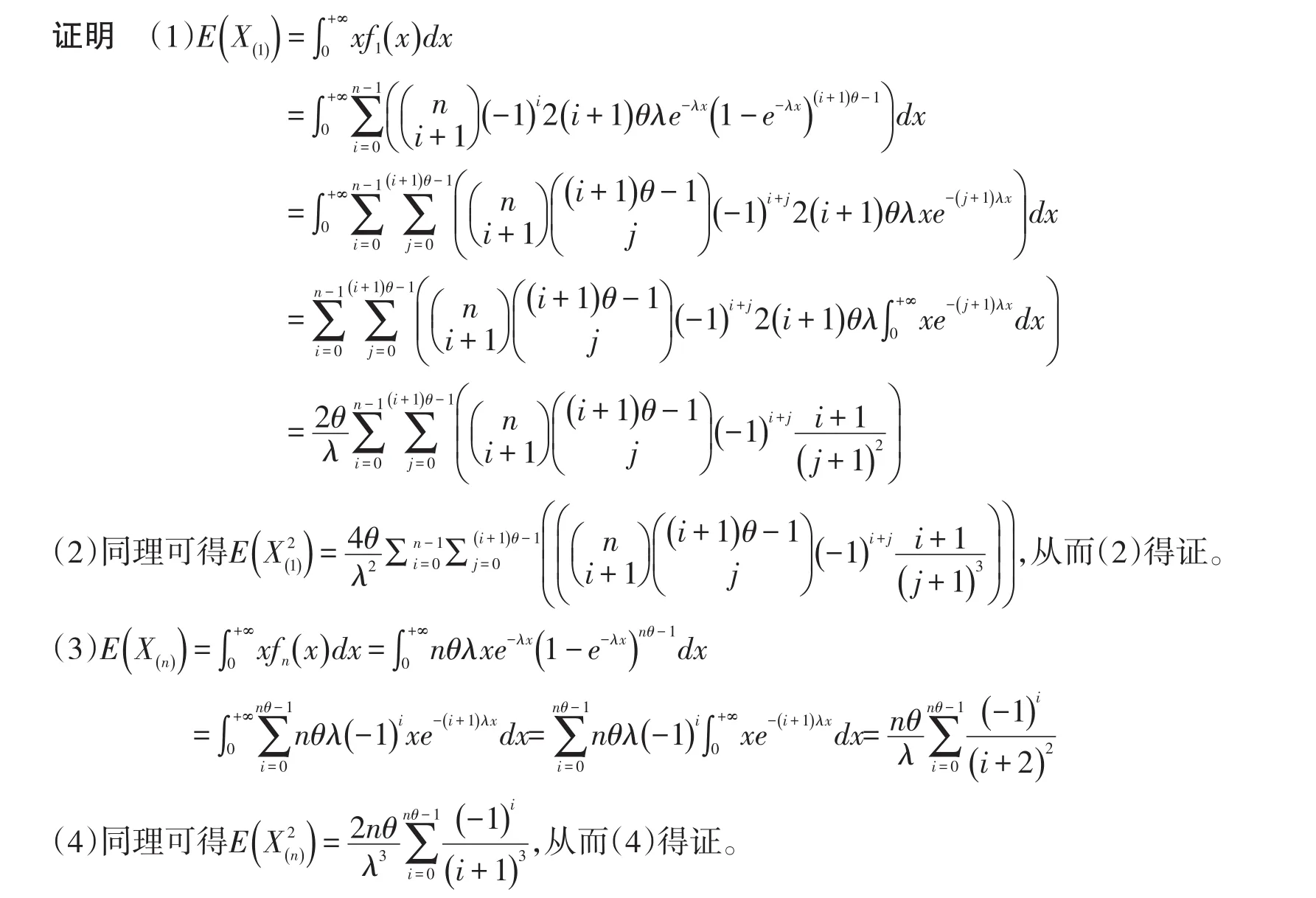
证明不妨设Y1=X（1），Y2=X（2）-X（1），令y1=x1，y2=x2-x1，则x1=y1，x2=y1+y2，其雅可比行列式|J|=1，从而由定理1中的（1）知（Y1，Y2）的联合密度函数为

另一方面，根据定理1可得y1的密度函数为

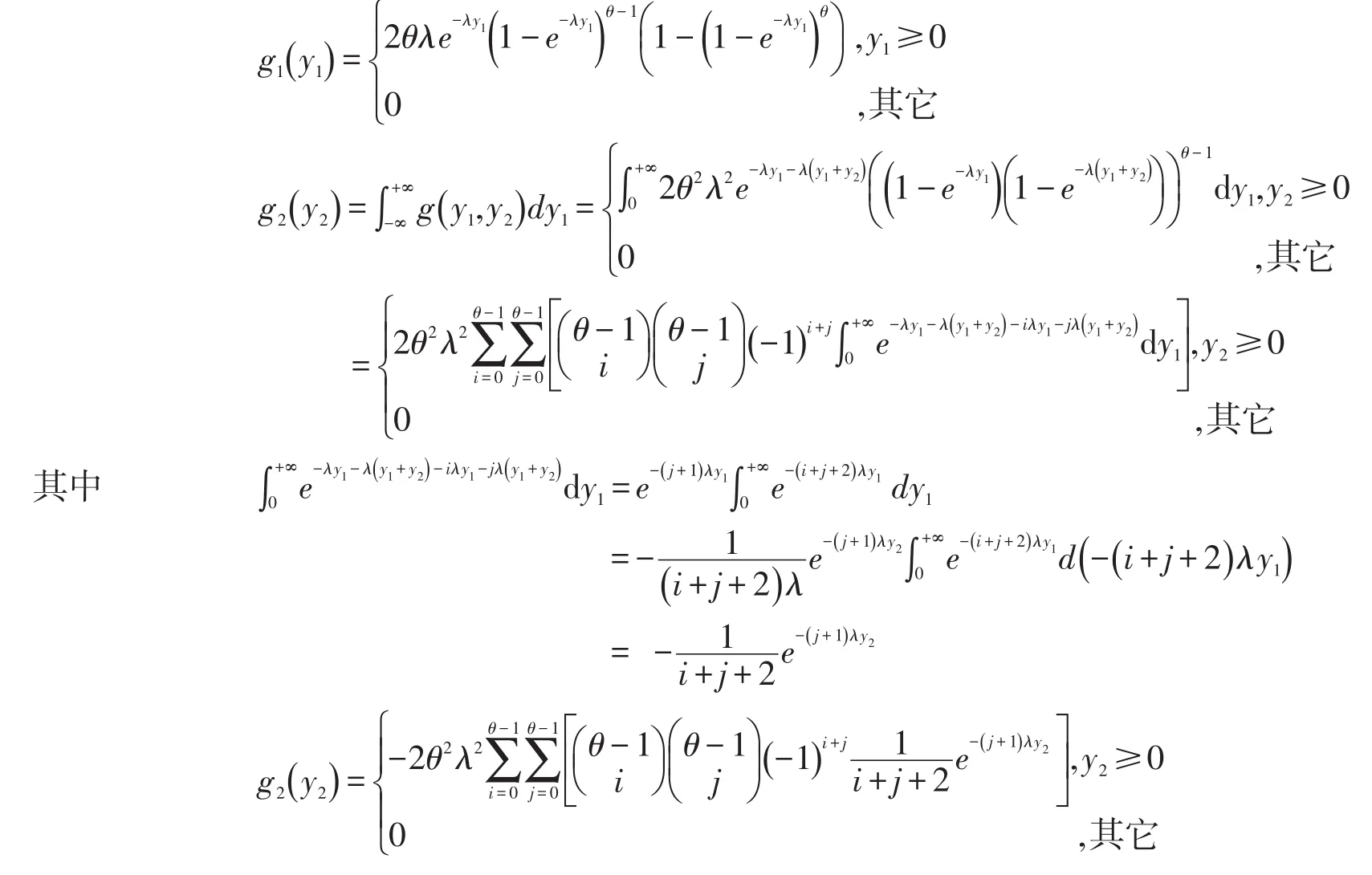
显然g（y1，y2）≠g1（y1）g2（y2），故X（1），X（2）-X（1）不独立且不同分布。

同理可证如下定理：

2　结语

［1］匡能辉.拉普拉斯分布顺序统计量的分布性质［J］.徐州师范大学学报，2009，27（3）：34-37.

［2］匡能辉.三参数Pareto分布顺序统计量的分布性质［J］.郑州大学学报，2011，43（2）：10-15.

［3］匡能辉.关于Gamma分布顺序统计量的分布性质［J］.兰州理工大学学报，2013（3）：166-168.

［4］匡能辉.关于瑞利分布顺序统计量的分布性质［J］.怀化学院学报，2009，28（2）：11-15.

［5］匡能辉.关于χ2分布顺序统计量的分布性质［J］.浙江师范大学学报，2009，32（4）：396-400.

［6］匡能辉.关于帕累托分布顺序统计量的分布性质［J］.甘肃联合大学学报，2009，23（4）：18-21.

［7］匡能辉.关于两参数瑞利分布顺序统计量的分布性质［J］.江西师范大学学报，2009，32（6）：678-651.

［8］姜培华，范国良.关于三参数威布尔分布顺序统计量的概率分布性质探讨［J］.统计与决策，2015，27（6）：27-30.

［9］姜培华.关于威布尔分布顺序统计量的分布性质［J］.安庆师范学院学报，2012，18（1）：47-50.

［10］姜培华.自由分布顺序统计量的函数的概率分布［J］.池州学院学报，2011，25（3）：9-11.

［11］姜培华.艾拉姆咖分布顺序统计量的概率分布及渐进性质［J］.南通大学学报，2015，14（2）：64-68.

［12］姜培华.双参数指数分布顺序统计量的概率分布性质［J］.哈尔滨师范学院学报，2013，29（5）：25-28.

［13］贺嘉，杜超雄.关于指数分布顺序统计量的分布性质［J］.湖南科技大学学报，2011，26（3）：125-128.

［14］王晓红，姜泽.关于幂分布顺序统计量的分布性质［J］.吉林师范学院学报，2011（4）：108-110.

［15］郭环.两参数广义指数分布的参数估计与数值模拟［J］.华中科技大学硕士论文，2013.

［16］茆诗松，王静龙，濮晓龙.高等数理统计理论［M］.高等教育出版社，2006：14-15.

［17］何朝兵，田彦伟.顺序统计量的分布［J］.成都大学学报，2008，27（2）：116-119.

［18］王伟.关于顺序统计量分布的一种证明［J］.长春大学学报，2002，12（6）：20-21.

Generalized Exponential Distribution Properties of Order Statistic

LI Juan， FAN Zi-miao，ZhouJu-ling
（School of Mathematical Science，Xinjiang Normal University，Urumqi，Xinjiang，830017，China）

In this article，we extract the sampleX1，X2…，Xnwhen general obey generalized exponential distribution，X（1），X（2），…，X（n）are their order statistics.The joint probability density function of（X（1），X（2），…，X（n））and the density functions of X（1）andX（n）are researched.Therefore the representation formulas of the mathematical expectation and variance of X（1）andX（n）are obtained And proving thatX（1），X（2）-X（1），…，X（n）-X（n-1）are not independent and different distribution.

The generalized exponential distribution；Order statistic；Mathematical expectation；Variance

O212.7

A

1008-9659（2016）03-0037-04

2016-04-20

李娟（1991-），女，新疆乌鲁木齐人，硕士研究生，主要从事概率论与数理统计方面的研究。

周菊玲（1968-），女，新疆哈密人，副教授，主要从事概率论与数理统计方面的研究。