概率组合与警告类型对合取谬误的影响

徐富明　李　欧　邓　颖　刘程浩　于会会

（华中师范大学心理学院暨湖北省人的发展与心理健康重点实验室；青少年网络心理与行为教育部重点实验室，武汉 430079）

概率组合与警告类型对合取谬误的影响

徐富明李欧邓颖刘程浩于会会

（华中师范大学心理学院暨湖北省人的发展与心理健康重点实验室；青少年网络心理与行为教育部重点实验室，武汉 430079）

概率判断中的合取谬误是指违反事件发生概率的合取规则，而认为包含多个独立事件的复合事件的发生可能性大于其中某些事件的发生可能性的一种概率判断偏差现象。本研究探讨了概率组合类型与警告类型及其交互作用对合取谬误的影响，结果表明概率组合类型、警告类型的主效应均显著，但并未发现二者对合取谬误的影响存在交互作用。

合取谬误；合取事件概率组合类型；警告类型

1　前言

Tversky和Kahneman指出，在概率判断中，如果个体认为两个合取项组成的合取事件“A且B”要比单个合取项“A”或“B”发生的可能性更大，那么就会出现合取谬误（conjunction fallacy）［1］，用数学表达即P（A∧B）≥P（A）or P（B）。根据集合关系，元素A∧B∈集合｛A，B｝，所以 P（A∧B）≤P（A）or P（B），显然合取谬误违反了这一规则。自合取谬误提出后，众多心理学家对这一现象进行了深入的探讨。Yates和Carlson根据合取事件的主观概率与其各个合取项的主观概率之间的关系，把合取谬误分为三种类型，即双重合取谬误（double conjunction fallacy）、单合取谬误（single conjunction fallacy）以及零合取谬误（zero conjunction fallacy）［2］。双重合取谬误指对合取事件的概率估计高于其各个合取项的概率；单合取谬误指对合取事件的概率估计高于其中一个合取项而小于另一个合取项；零合取谬误指对合取事件的概率估计低于其各个合取项的概率，即未出现合取谬误。

对该现象的解释机制，有从代表性启发式（representative heuristic）观点出发的因果模型理论（casual model theory）［1］，从事件惊奇值（surprise values）角度分析的潜在惊奇理论 （potential surprise theory）［3］，还有分析证据（evidence）对合取项或合取事件支持性的确认理论（confirmation theory）［4］，以及“齐当别”理论（the equate-to-differentiate theory）［5］、语义多样性观点［6］等。尽管上述理论都证实了合取谬误的存在并提出和验证了众多的心理机制，但有关合取谬误影响因素的研究仍较为少见。本文试图对合取谬误的影响因素进行一些有益的探索，以弥补该方面的不足。

合取事件的概率组合类型会影响个体表现出何种类型的合取谬误及其可能性。Yate和Carlson依据符号加和理论（signed summation theory）提出用QLI（qualitative likelihood index，质性可能指数）表示事件的可能性，QLI与代表性相似，但其具有正负两个维度［2］。不可能事件的QLI为负，事件越不可能QLI越小；可能事件的QLI值为正，可能性越大其QLI值越大；合取事件的QLI值为其各个合取项的QLI值之和。如果以P（A）表示事件A发生的可能性，当事件A为可能性事件、中性事件和不可能性事件时，P（A）分别为正值、零和负值。因此A与B的合取事件的可能性可以表示为P（A&B）=P（A）+P（B）。如果以P（A）表示事件A发生的可能性，对于两个可能事件A与B，P（A）＞0，P（B）＞0，可知此时合取事件A&B，P（A&B）＞P（A）且P（A&B）＞P（B），产生双重合取谬误；对于可能事件A，P（A）＞0，不可能事件B，P（B）＜0，那么此时合取事件A&B，P（A&B）＜P（A）且P（A&B）＞P（B），产生单合取谬误；对于两个不可能事件A与B，P（A）＜0且P（B）＜0，可知此时合取事件A&B，P（A&B）＜P（A）且P（A&B）＜P（B），产生零合取谬误。而Costello依据概率偏差理论预测合取谬误在一个高概率事件和低概率事件组合时最易发生，其次是高概率事件和高概率事件组合时，最后是低概率事件和低概率事件组合时［7］。Nilsson和Andersson在足球赌博的任务情景中验证了上述预测，他们发现人们更偏好投注两支赢率差异较大的球队的组合［8］。此外，Fisk和Pidgeon在其实证研究中发现当两个高概率事件组合时，双重合取谬误发生的概率并不高［9］。而且根据加权平均模型（weighted averaging model）的研究，人们判断合取事件的概率并不是根据合取概率或者条件概率等进行比较，而是对多个合取项的概率进行简单的加权平均［9］。Fantiona等人在实验中比较了被试对合取事件的概率判断与乘法、加法以及平均模型的拟合度，结果被试的判断与平均模型的拟合度最优，而且他们还发现当合取事件是由两个发生概率相差较大的合取项组成时，合取谬误的程度最大［10］。但在后续研究中，Tentori，Crupi和Russo却发现合取谬误的大小与事件发生概率的差异无关［11］。针对相关研究中存在的矛盾，我们有必要对何种概率组合类型对合取谬误产生的影响最大做进一步研究。

Cheng和Wu在研究指导语中的警告对框架效应的影响时，发现适当的警告可以减弱框架效应对人们的影响［12］。合取谬误和框架效应同样作为一种非理性决策，适当的警告应该也可以减弱合取谬误对人们的影响。因此，本文的目的是探究指导语中的警告能否减弱合取谬误对人们的影响，同时探究警告和概率组合类型对合取谬误的交互影响。

基于以上分析，我们提出如下假设：

H1：合取事件概率组合类型会影响合取谬误，具体为，合取事件由两个高概率事件组合时，被试表现出双重合取谬误，且合取谬误的表现较强；合取事件由高概率事件和低概率事件组合时，被试表现出单合取谬误，且合取谬误的表现最强；合取事件由两个低概率事件组合时，被试表现出零合取谬误。

H2：警告类型会影响被试的合取谬误，具体为，无警告时最易表现出合取谬误，其次是间接警告，直接警告条件下最不易出现合取谬误。

H3：合取事件概率组合类型和警告类型对被试合取谬误的影响存在交互作用。

2　方法

2.1被试

随机选取国内某高校在校生443名，其中本科生386名，大一120名，大二58名，大三147名，大四61名；研究生57名，研一23名，研二18名，研三及以上16名；男生270名，女生173名；理科139名，工科209名，文科95名。

2.2实验设计

实验为3（合取事件概率组合：高高概率、高低概率、低低概率）×3（警告类型：无警告、直接警告、间接警告）组间设计，因变量是合取谬误的发生比例和类型，合取谬误类型有三个水平：双重合取谬误、单合取谬误和零合取谬误。在实验中，虽然每一个被试组都可能表现出三种谬误类型，但每一名被试只可能表现出一种谬误类型，所以只标记所出现的谬误类型即可。然后统计每种实验条件下三种谬误类型的数目以及比例等数据，而合取谬误的发生比例为双重合取谬误和单合取谬误的频数在三种谬误类型总频数中所占的比例。

2.3实验材料

首先我们在预实验中进行单一合取项的概率估计任务，并将概率估计大于0.5的事件确定为高概率事件，而将小于0.5的事件确定为低概率事件，而且尽可能选取估计概率接近于极值的合取项作为高低概率事件。此外，根据合取谬误的研究范式，我们将经典的Linda、Bill问题［1］改编为李娜和李明问题，分为3（概率组合类型）×3（警告类型）=9种任务情景。

2.4实验程序

首先让被试阅读一段关于人物（李娜或李明）的描述，然后估计后面每个事件发生的概率。当预测该事件发生的概率值处在0%与50%之间时，表示该事件较不可能发生；当预测该事件发生的概率值处在50%与100%之间时，表示该事件较可能发生。实验结束后每位被试会得到一份精美的礼品。

指导语分为无警告语和有警告语两种，其中有警告语的指导语又分为两种：（1）间接警告，提醒人们判断中会出现判断偏差，并注意防范偏差的发生；（2）直接警告，介绍合取谬误的概念，并提醒人们判断中会出现合取谬误，要注意审查信息防止合取谬误的发生。

3　结果与分析

首先，分析合取谬误是否存在以及每种谬误类型在9种条件下的情况，结果如表1所示。从表1最后一列可知，出现双重合取谬误、单合取谬误和零合取谬误的可能性分别为13%、42%、45%，即在该问题中有55%的被试表现出合取谬误，证实了这种偏差的存在。

然后检验人口学变量以及概率组合类型、警告类型对合取谬误的影响，结果见表2。

由表2可知，性别（χ2（2）=0.18，p=0.92）和专业类别（χ2（4）=3.91，p=0.42）对合取谬误的影响不显著，但年级（χ2（12）=21.47，p＜0.05）对合取谬误的影响显著；概率组合（χ2（4）=27.97，p＜0.01）、警告类型（χ2（4）=16.49，p＜0.01）对合取谬误的影响均显著，即二者的主效应均显著。

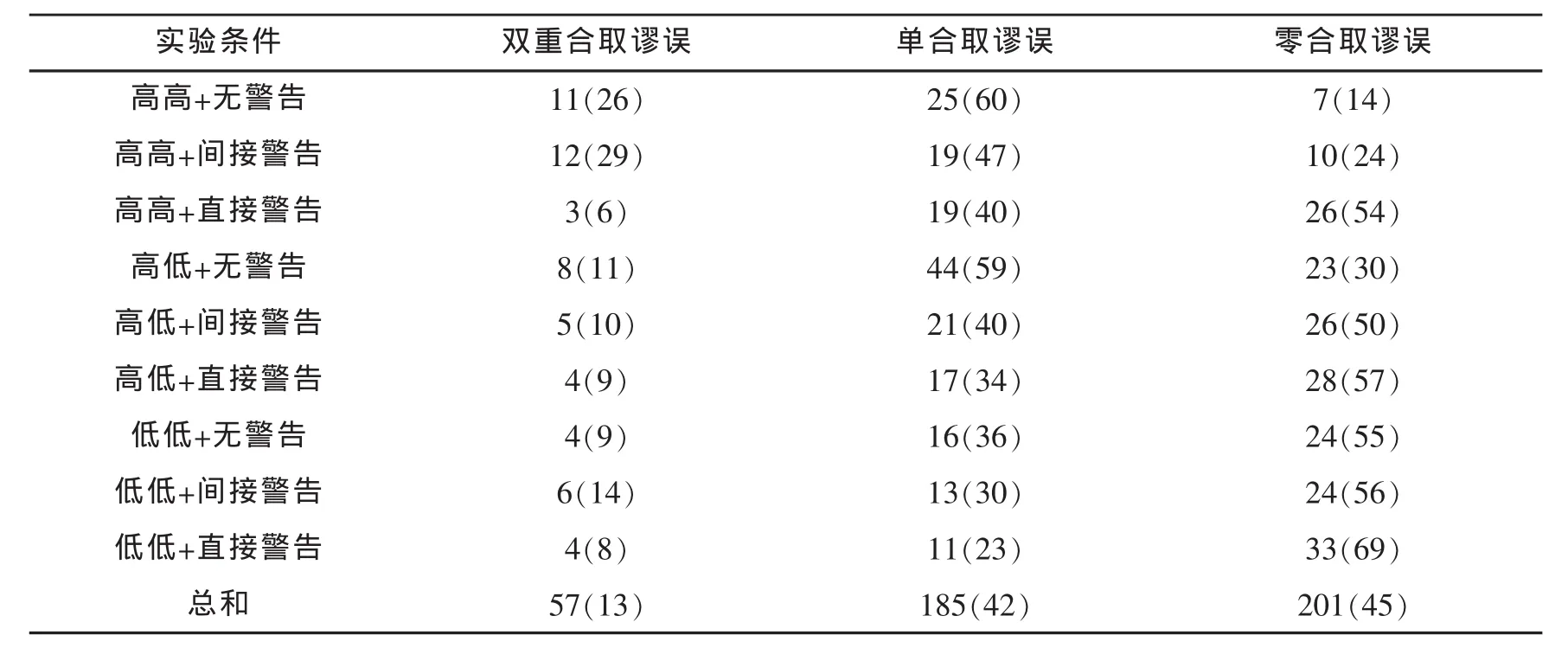
表1　合取谬误类型人数分布

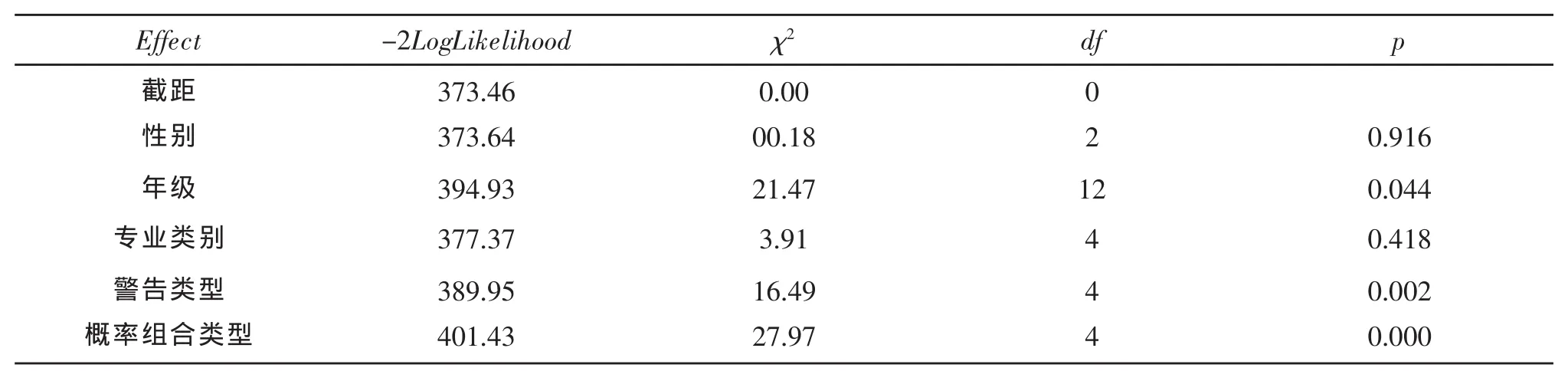
表2　似然比检验

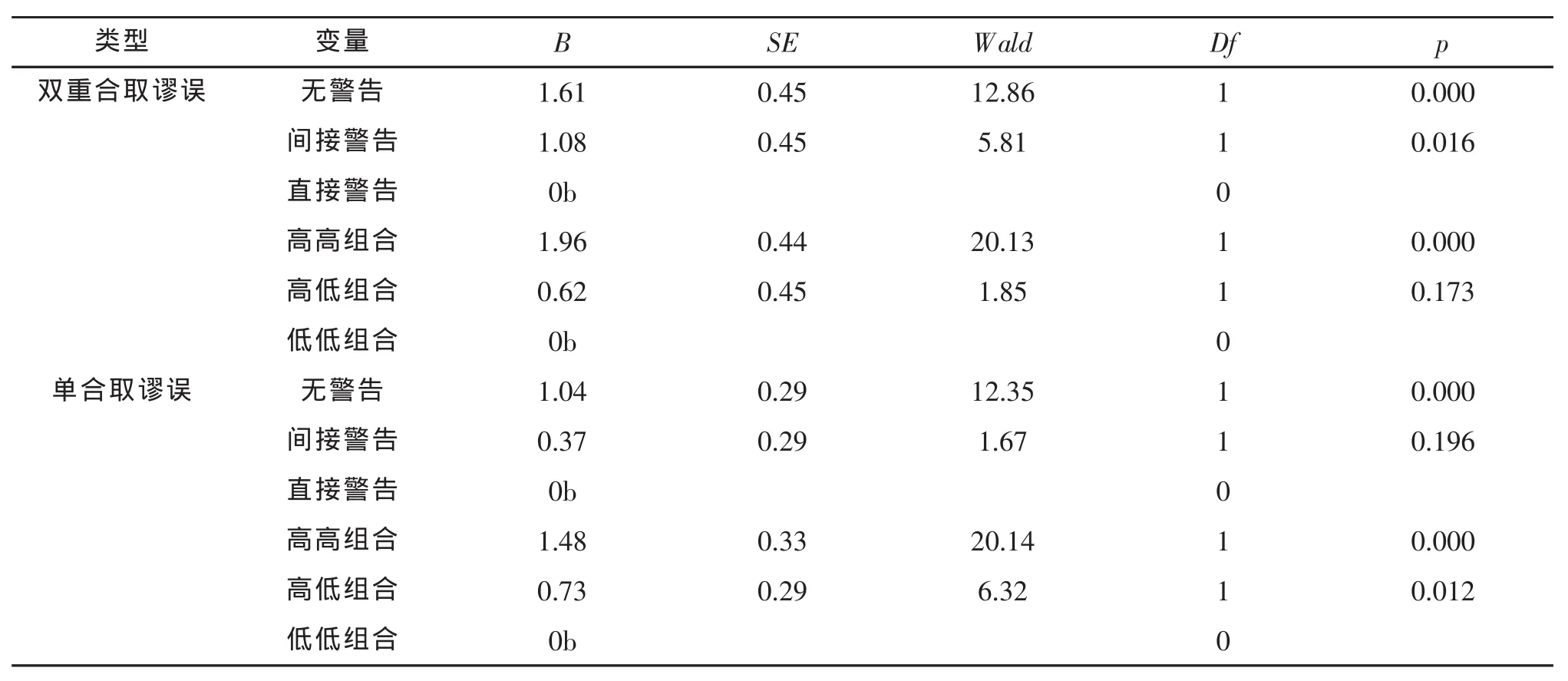
表3　参数估计

进一步进行参数估计检验，结果见表3。从中可以看出警告类型对双重合取谬误是正向预测，即无警告时最易表现出双重合取谬误，其次是间接警告，直接警告相较于其它两种警告形式表现出较少的双重合取谬误。而对于单合取谬误来说，预测方向基本一致，无警告时最容易产生合取谬误，但间接警告和直接警告对合取谬误的预测程度一致，即两种警告方式产生的合取谬误率无显著差异。

而合取事件概率组合类型对双重合取谬误和单合取谬误也均是正向预测，即高高概率组合最易表现出合取谬误，其次是高低概率组合，低低概率组合相较于其它两种组合表现出较少的合取谬误；同时相较于零合取谬误，高高概率组合表现出明显的双重合取谬误和单合取谬误，高低概率组合仅表现出显著的单合取谬误。各交互效应也不显著，只有年级和合取事件概率组合类型的主效应显著，其中年级的主效应表现在研究生相较于本科生产生的合取谬误较少。

最后，分析合取事件概率组合与警告类型对合取谬误的交互作用。以合取谬误类型为因变量时，对数据进行多项logistic回归的主效应分析，结果表明模型拟合较好。进一步分析影响合取谬误的自变量，数据分析结果见表4。

表4　似然比检验

由表4可知，合取事件的概率组合类型、警告类型对合取谬误影响的交互作用不显著（χ2（8）=7.93，p=0.441）。进一步进行参数估计检验，仅发现高高概率组合条件下，无警告和直接警告水平间存在双重合取谬误的显著差异（p＜0.05）。

综上，本实验首先验证了合取谬误以及双重合取谬误、单合取谬误和零合取谬误三种谬误类型的存在，然后探讨了合取事件概率组合类型对合取谬误的影响。结果发现，除年级外，其他人口学变量对合取谬误无显著影响，但是合取事件概率组合类型对合取谬误有显著影响。在单合取谬误上，验证了Yates和Carlson提出的符号加和理论的预测：合取谬误率最大的是高高概率组合，其次是高低概率组合，低低概率组合最不易表现出合取谬误［2］。而在双重合取谬误上，高高组合和高低组合的差异并不显著，这与Costello所做出的“双重合取谬误在两个高概率事件组合时最易出现”的预测［7］不一致。除此之外，在各个实验条件下均出现了三种合取谬误，所以综上得出：实验结果并不支持假设H1。

其次，本实验基本验证了假设H2，直接警告相较于其它两种警告形式更有助于抑制合取谬误，但仅仅限于双重合取谬误。而在单合取谬误中，两种警告方式并无显著差异。

再次，本实验探讨了合取事件概率组合类型和警告类型对合取谬误的影响，合取事件概率组合类型和警告类型的交互作用对合取谬误的影响不显著，即不支持假设H3。这说明外界警告并不能帮助被试克服问题特征的影响，也就是说，问题本身特征引起的合取谬误很难通过外界因素干预而克服。

4　讨论

4.1合取谬误的跨文化一致性

自Tversky和Kahneman首次发现合取谬误现象之后，众多研究发现合取谬误在西方文化背景中是普遍存在的，然而国内的相关研究却较为少见。本文研究发现，在无其他因素干扰下，有55%的被试表现出合取谬误，可见合取谬误在中国文化背景中也是稳定存在的。此外，本文还证明对合取谬误的划分方式（双重合取谬误、单合取谬误、零合取谬误）是成立的，确实存在三种类型的合取谬误。

4.2合取谬误的变化性

本文还发现合取事件的概率组合类型以及警告类型会影响被试是否表现出合取谬误。相对于零合取谬误，高高概率组合最易表现出合取谬误，其次是高低概率组合，低低概率组合最不易表现出合取谬误，从而说明合取项之间的概率差异确实会对合取谬误产生影响。该结果并不如加权平均模型所做的预测：高低组合表现出最高的合取谬误。而且加权平均模型无法解释双重合取谬误的现象，但就单合取谬误来说，高低组合却表现出最高的合取谬误率，也说明了加权平均模型有一定的正确性。然而Tentori等人对加权平均模型所提出的增加合取项使合取事件概率增加进而导致合取谬误的观点提出了质疑，他们将模型改进为P（A∧B/e）=w·P（A/e）+（1-w）·P（B/e）［11］。实验中将合取项A发生概率设置为低水平，合取项B可以得到证据e（关于人物特性的描述性信息）的确认，但发生可能性不太大，而￢B得不到e的确认，却有更大的发生概率。而加权平均模型假设，增加的合取项可以使合取事件的发生概率增加从而导致合取谬误，那么在合取项为B和￢B的情况下，都会出现合取谬误。然而实验结果却表明只有在合取项为B的条件下，也就是只有合取项能够得到证据e的确认时才会出现合取谬误。因此加权平均模型尽管很好地拟合了实验中的某些数据，但对实验数据的解释可能并不正确。而符号加和理论也不能很好地解释为何在三种概率组合下均出现三种合取谬误类型。所以针对本研究的实验结果，我们认为确认理论［4］能够做出很好的解释。确认理论认为合取事件（A∧B）得到e的确认使其条件概率较先验概率（或本有的概率）增加更多，而合取项的概率增加值很小或者没有。在概率判断中，被试并不比较合取事件的概率或条件概率的大小，而是根据确认性进行事件发生可能性的判断。如果用C表示确认度，那么合取事件的确认度C1=P（A∧B/e）-P（A∧B），合取项的确认度C2=P（B/e）-P（B）、C3=P（A/e）-P（A）。在三种概率组合条件下，双重合取谬误产生即C1＞C2且C1＞C3，单合取谬误即C1＞C2或C1＞C3，零合取谬误即C1＜C2且C1＜C3，而在每种条件下，不同被试对三个事件（一个合取事件，两个合取项事件）主观赋值的差异导致不同的C1、C2、C3，进而产生三种谬误类型。

此外，实验同时证实了警告类型也会影响被试表现出合取谬误，无警告时被试最易表现出合取谬误，间接警告时被试较容易表现出合取谬误，直接警告时被试最不倾向于表现出合取谬误。可见警告越直接、警告程度越深，被试对问题的认知加工深度越深，从而较少受问题表述方式的影响，合取谬误也就更难发生。

但实验并未验证概率组合类型与警告类型对合取谬误的影响存在交互作用。由此可知，外界干预——警告——在概率组合类型对合取谬误的影响之中不起调节作用。这可能是因为合取事件的概率组合类型对合取谬误的影响程度较深，本研究所采用的警告程度还不足以对其产生抑制作用。这也间接证明了事件特征对合取谬误的影响更稳定、更深刻。

本研究还发现被试的年级会对合取谬误产生影响。低年级被试倾向于表现出双重合取谬误，但更不易表现出单合取谬误，这可能是由各年级组之间的认知能力差异导致的。例如Oechssler，Roider和Schmitz的研究发现，高认知能力的被试发生合取谬误的概率较低，但是合取谬误现象在高认知能力的被试中仍然存在［13］。同时这些人口学变量的主效应并不稳定，年级主效应的产生也可能是因为本实验仅将人口学变量作为控制变量，对被试的选取不均匀所致。

综上所述，本研究证实了合取谬误的稳定性，发现了合取事件的概率组合类型以及警告类型对合取谬误的影响。这些研究可以引导我们采取更合理的措施应对合取谬误的不利影响，做出更准确的判断，从而做到决策最优化。

5　结论

合取谬误在中国文化背景中仍然存在，而且合取谬误的三种类型（双重合取谬误、单合取谬误、零合取谬误）的划分是成立的。

相对零合取谬误，高高概率组合最易表现出合取谬误，其次是高低概率组合，低低概率组合最不易表现出合取谬误；同时高高概率组合表现出明显的双重合取谬误和单合取谬误，高低概率组合仅表现出明显的单合取谬误。

被试在无警告、间接警告、直接警告的类型下表现出合取谬误的倾向性是递减的；而警告与概率组合类型的交互作用不显著。

低年级被试倾向于表现出双重合取谬误，而较少表现出单合取谬误，但这种影响并不稳定。

1Tversky A，Kahneman D.Extensional versus intuitive reasoning：The conjunction fallacy in probability judgment.Psychological Review，1983，90（4）：293-315.

2Yates J F，Carlson BW.Conjunctionerrors：Evidenceformultiplejudgmentproceduresincluding“signed summation”.Organizational Behavior and Human Decision Processes，1986，37（2）：230-253.

3Fisk J E，Pidgeon N.Conditional probabilities，potential surprise，and the conjunction fallacy.The Quarterly Journal of Experimental Psychology：SectionA，1998，51（3）：655-681.

4Crupi V，Fitelson B，Tentori K.Probability，confirmation，and the conjunction fallacy.Thinking&Reasoning，2008，14（2）：182-199.

5Li S.Equate-to-differentiate approach：An application in binary choice under uncertainty.Central European Journal of Operations Research，2004，12（3）：269-294.

6Hertwig R，Benz B，Krauss S.The conjunction fallacy and the many meanings of“and”.Cognition，2008，108（3）：740-753.

7Costello F J.How probability theory explains the conjunction fallacy.Journal of Behavioral Decision Making，2009，22（3）：213-234.

8Nilsson H，Andersson P.Making the seemingly impossible appear possible：Effects of conjunction fallacies in evaluations of bets on football games.Journal of E-conomic Psychology，2010，31（2）：172-180.

9Fisk J E，Pidgeon N.Component probabilities and the conjunction fallacy：Resolving signed summation and the lowcomponent model in a contingent approach. Acta Psychologica，1996，94（1）：1-20.

10Fantino E，KulikJ，Stolarz-Fantino S，et al.The conjunctionfallacy：Atest of averaging hypotheses. Psychonomic Bulletin&Review，1997，4（1）：96-101.

11Tentori K，Crupi V，Russo S.On the determinants of theconjunctionfallacy：Probabilityversus inductive confirmation.Journal of Experimental Psychology：General，2013，142（1）：235-255.

12Cheng F F，Wu C S.Debiasing the framing effect：The effect of warning and involvement.Decision Support Systems，2010，49（3）：328-334.

13Oechssler J，Roider A，Schmitz P W.Cognitive abilities and behavioral biases.Journal of Economic Behavior&Organization，2009，72（1）：147-152.

The Effect of Probability Combination and Warning Type on Conjunction Fallacy

Xu Fuming，Li Ou，Deng Ying，Liu Chenghao，Yu Huihui
（School of Psychology，Central China Normal University；Key Laboratory of Human Development and Mental Health of Hubei Province；Key Laboratory of Adolescent Cyberpsychology and Behavior（CCNU），Ministry of Education，Wuhan 430079）

The conjunction fallacy in probability judgment refers to a phenomenon of probability judgment bias，which results from violating the conjunction rules of event occurrence probability and regarding that the occurrence probability of conjunction event that contains multiple independent events is greater than that of conjunct events in it.This study examined the effect of probability combination，warning type and the interaction between them on the conjunction fallacy.The results suggested that the main effects of the two variables both reach ed the significant level.However，there was no interaction.

conjunction fallacy；probability combination type of the conjunctive event；warning type

徐富明，男，教授，博士。Email：fumingxu@126.com