焊管厂成品库库存优化研究

时兵兵，杜天苍

(1.北京化工大学，北京 100029；2.北京石油化工学院，北京 102617)



焊管厂成品库库存优化研究

时兵兵1，2，杜天苍2

(1.北京化工大学，北京 100029；2.北京石油化工学院，北京 102617)

以国内传统和现代物流库存成本管理为依据，对焊管厂成品库库存进行建模及优化设计，对采购成本、保管成本和缺货成本进行了分析。在以库存成本为优化目标的模型上加入以库存时间为优化目标的模型，并使其结合，得到资金制约、仓库容积制约等情况下最优订购批量的弹性区间，在节约订货总成本的同时，使焊管厂的库存时间大大减少，让焊管厂的库存资金使用更加灵活，确保库存资源的有效利用。

库存优化；仓储管理；联合订购；经济批量

库存管理是以顾客需求为第一前提，从库存这一关键点进行优化，最大限度地降低库存量，加强企业影响力和竞争力。库存水平的优劣给企业经营与生产带来直接影响，适当的库存量可以防止交货期延误、产品供应中断等问题，减少多余开支，调节市场对产品的季节性需求，适应各种需求变动，是企业保持连续稳定生产的必要条件。而库存过量需要大量库存费用的支出，造成成本增加、利润减少，同时必然暴露出量产与销售的矛盾以及各种生产阶段的问题，因此急需从供应链管理方面改善库存问题。

笔者分析了焊管厂运营现状及目前存在的库存问题，着重对成品库存的控制和优化进行分析和研究，并对产库存结构进行设计，保证成品交库、盘盈交库、移库交库、外委交库、场外库存、待平整库存等处于合理数量，保证产入产出处于均衡、稳定、有序的状态。最后，针对问题提出解决对策和改善方案，达到降低库存成本，减少库存时间的目的，提高库存控制能力。

1　库存成本管理模型

1.1库存成本管理方法的选择

常用的传统库存成本管理方法有物流库存成本管理ABC分析法[1]、定期订货管理法和经济订货批量法。现代库存成本管理方法有物料需求计划(MRP)、制造资源计划(MRPII)、分销资源计划(DRP)和准时方式(JIT)。

随着物流行业的高速发展，库存成本管理的重要性在企业竞争中越来越突出。传统的库存成本管理方法已不能适应现代物流的发展。ABC管理法对库存成本管理要求低，但使用手工分类计算，因而比较粗略。用定期订货管理法进行订货不仅运输成本较高，还需要对未来销售量进行精准预测，因而使用起来也有一定的局限。现代物流库存成本管理方法虽然较为先进，但对于许多企业有多种条件难以满足，也就是说还没有到可以立即采用的时机。

因此，企业选择何种库存成本管理方法还需要根据企业自身判断，从系统可靠性、维护费、系统资源的使用率、系统活性等方面综合考虑，选择适合企业自身的方法进行管理。

1.2经济订货量基本模型

经济订货批量的模型(EOQ模型)是现代企业最普遍、最常使用的定购货物的方式。最优订货量反映了现有成本与订货成本之间的平衡:用Q表示货物每次的订购批量，大批量Q的、低频率的订货方式会造成较高的平均库存水平，从而使持有成本上升；小批量Q的、高频率的订货导致经常性的订货，这样同样迫使年成本上升[2]。只有采取经济型订单批量，订货批量在订货量与订货次数两者之间找到平衡，最小化总成本。

设某种货物在单位时间以恒定需求量消耗库存量，库存量经过时间T后由最高下降到零，此时定货则库存量立即补充至最高[3]。模型以此为1个消耗-补充周期，重复进行。对该模型，假设：(1)某种货物年需求量已知，为常量，以D表示；(2)货源充足，订货量无限制；(3)采购、运输单价不变；(4)订货提前期已知，为常量；(5)货物补充及时到位；(6)缺货成本为零；(7)存货不存在变质[4]。

假如将库存成本分为采购成本Ca、保管成本Cc和缺货成本Cs，某种货物每次的订购批量为Q，每次订货成本为K，货物单价为P，单位储存变动费用为Kc，采购与保管固定费用分别为F1、F2。那么，该种货物年储存总成本：

(1)

如果不考虑不会引起存货成本的变化的常数，对其求导，可得该种货物最佳经济订货模型:

(2)

2　焊管厂成品库库存成本优化研究

2.1焊管厂当前库存状况

某焊管厂产品为石油天然气管、石油套管、结构管，年产量15万t。近年来，随着焊管厂业务面的多方位开展，市场压力随之增加，传统库存管理的问题渐渐的浮出水面，包括库存资金比例过重、存货周转率偏低等。由于焊管厂生产管理中各工序的生产能力和运行特性不一致等问题，到2014年年底，焊管厂已产生了巨额的库存积压。与此同时，大量积压的库存使不合格品不能得到及时处理，混杂在合格品中，更增加了处理难度。2014年4月，预处理成品库存达到22 675 t，待场外库存达到14 423 t，待平整库存为8 742 t，成品待交库5 464 t。4月份库存达到51 304 t，成品发运只有37 081 t，造成钢管大量积压，占用资金巨大。此外，由于钢管的随意摆放，符合生产要求的钢管无法及时送到生产线上，使得计划停顿、欠产，单月合同亏欠已达4 136 t，严重影响了客户满意度。由于相应管理方法不足，生产中不合格品很难得到妥善而及时的处理，有的甚至被误当作正常品流通，结果库存中不合格品比例逐步上升，进而造成库存结构不合理，给正常管理带来很大难度。所以，公司需使用更为系统的管理模式，寻找符合自己情况的库存管理方案来解决当下问题。

2.2成品库库存成本模型

对库存的优化目标通常是让与库存决策有关的各项消费的总成本(包括采购成本、保管成本、缺货成本)达到最小水平[5]。

2.2.1采购成本

采购费包括订货费和可变费用。货物如果是向外采购，那么每进购一批货物都需要支出采购员的差旅费和运输费等相关费用，在货物入库和货物堆放时也会产生一定的费用。向外采购将支出一笔采购费，他跟批量大小相关。即使库存货物由企业内部生产，也存在设备消耗、清理和工人管理费等生产费用。而生产中的可变生产成本随批量大小改变，是每批的可变费用，他与批量大小之间也不是线性相关的。

假设某种货物每批固定的订货费为K，单位价格为P，每批的订购批量为Q，年需求量为D，那么年总采购成本的费用模型为:

(3)

2.2.2保管成本

保管成本为存放在仓库而产生的有关费用和现金支出，包括库存税、货物保险、货物搬运费、仓库空间占用费、库存资金占用费、管理员工资，以及货物丢失、变质、损坏带来的损失等。假设这些费用与平均库存量I线性相关，于是可以建立库存保管成本的费用模型。对于焊管厂来说，I(t)表示不同时间段焊管的平均库存量。那么，在(0，T)时间内的平均库存可表示为:

(4)

设C1为单位时间内单位货物的保管费用，那么总库存保管费用可表示为：

(5)

2.2.3缺货成本

在对焊管厂建立缺货损失费用模型时，假设缺货总数为b，每吨所缺成品单位工时的违约费用为C1。在客户撤销合同或者同意用其他货物代替的情况下，总缺货损失费用模型为C1b。 若客户在缺货时同意延期交货，那么，损失费会与延期交货的时间相关，并且与平均缺货费用成正比。设单位所缺货物延期单位时间所造成的损失费用C2表示。

(6)

那么，在(0，T)时间段内的总缺货损失费模型可表示为：

(7)

2.3具有弹性的焊管厂库存优化改进模型

目前，焊管厂的库存包括生产库存、销售库存和积压库存，是一个多品种生产的库存系统。由于每天成品入库、出库频繁，长此以往库存管理任务艰巨，需要对其进行科学分析，利用有效方法进行指导，这样才能减少库存问题的出现。

一般情况下，通过经济批量法模型可以得到一个库存成本最少情况下的最优订货批量，他是1个固定参考值。然而，为应对资金周转方面问题，在多数情况下，财务管理使用弹性预算，希望订货批量是1个可选择区间而不是1个固定参考值，所以需要对库存模型进行一些改进。考虑到资金制约、仓库容积制约的情况，在以总库存成本为优化目标的模型基础上加入以库存时间为优化目标的模型，并使两者结合得到一个弹性区间，可以让焊管厂的库存资金有更多选择决策，使用更加灵活。

焊管厂产品种类繁多，每种钢管的平均库存时间由于相应订单要求不同以及生产周期不同而有所区别。在缺货成本为零且物资消耗速率匀速的情况下，为了建立1个具有普遍性的以库存时间为目标的优化模型，引入以下定义：Ki表示第i种钢管的订货成本；Pi表示第i种钢管的单位价格；Ui为第i种钢管的单位保管成本；Di为第i种钢管的年需求量；Hi为第i种钢管每次补充库存订货的固定周期；Ti为第i种钢管单位钢卷在生产线上的轧制时间；Ii为第i种钢管单位钢卷在生产工艺各机组间平均滞留时间；Qi为第i种钢管每次进购相应原材料的批量。

那么n种钢管的年储存总成本：

(8)

n种钢管从原料的订货入库到加工为成品交库的年总耗时之和为:

(9)

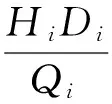
实际生产中，需要考虑生产总时间的限制和资金、仓库容积限制。用T表示最大生产总时间，V表示仓库的总容积，F表示最大订货资金，vi为第i种钢管每卷的占用体积，可得约束条件：

(10)

(11)

(12)

由式(8)、式(11)、式(12)可得以库存总成本为优化目标的非线性规划模型，根据极值的拉格朗日乘子法，引入乘子θ1,θ2:

(13)

由求极值的最优性条件:

(14)

可求得以库存总成本为优化目标的最优订购批量:

(15)

由式(9)～式(11)可得以库存时间为优化目标的非线性规划模型，根据极值的拉格朗日乘子法:

(16)

由求极值的最优性条件式(14)可求得以库存时间为优化目标的最优订购批量:

(17)

(18)

2.4应用分析

以焊管厂生产的J55套管、Q235B结构管2种钢管为例，根据生产计划统计出过去3年与上述以库存时间为目标的优化模型相关的生产管理数据，结果如表1所示。

表1　焊管厂钢管生产管理数据

根据实际情况设定焊管厂最大库存资金限制为F=1 200万元；钢管仓库最大容积V=7 200 m3；年生产总时间限制为T=48 000 h；单位钢管占用体积为2 m3。那么，可以算出每种钢管原材料每次的最优进购批量Qi，其结果与实际进购批量的比较如表2所示。

表2　最优进购批量与实际进购批量对比

从表2可以看出， 通过此库存优化模型得到的最优进购批量在节约订货总成本的同时，也能使焊管厂的库存时间大大减少，提高整体生产效率，最后的计算结果为一个弹性区间，以缓解库存资金压力。当库存资金紧张时，选择订货成本最少的决策，节省更多资金；当库存资金充裕时，选择库存时间最少的决策，节省更多库存时间。

3　结论

分析了焊管厂成品库库存问题，以国内传统和现代物流库存成本管理为依据，对其进行建模及优化设计。应用经济批量法在以库存成本为优化目标的模型基础上进行改进，加入以库存时间为优化目标的模型，并使其相互结合，得到资金制约、仓库容积制约等情况下最优订购批量的弹性区间。用改进后的模型进行现场数据分析，结果表明，用此模型在节约订货总成本的同时，也能使焊管厂的库存时间大大减少，让焊管厂库存资金使用更加灵活，提高库存资源利用率和整体生产效率。在保障生产和消耗的动态平衡为前提下，为客户提供更好的服务质量。

[1]孙莹，鲍新中，王宁.考虑缺货的供应链联合库存成本分析及收益分配[J].北京科技大学学报，2012，10：1205-1212.

[2]李珍萍，胡洁琼，赵菲.东莞市某企业库存控制策略研究[J].物流技术，2013，13:394-396.

[3]栾少群，刘丽兰，程功勋，等.EOQ法随机库存预警模型研究与应用[J].现代制造工程，2011(5):31-35.

[4]何芬，翁玉婷，张玲玲，等.库存成本的分解及结构[J].物流工程与管理，2010，32(11):35-36.

[5]赵英会.EOQ模型在企业库存成本优化中的应用[J].统计与决策，2015，13:182-185.

A Study on Inventory Optimization for Product Storeroom of Welded Pipe Industry

SHI Bing-bing1,2, DU Tian-cang2

(1.Beijing University of Chemical Technology, Beijing 100029， China;2.Beijing Institute of Petrochemical Technology, Beijing 102617， China)

According to the traditional and modern logistic inventory cost management, modeling and optimization design of welded pipe industryproduct storeroom is done.The purchasing cost, storage cost and shortage cost areanalyzed as well.Based on the model, whichtakesinventory cost as the optimization goal, a new model which adds time as anotheroptimization goal, a variable intervalof optimum order batch is obtained, within constraints of both funds and warehouse space.Meanwhile, the total ordercosts can be saved, so doesthe inventory time of the welded pipe industry, which renders the industry more flexibleon the use of stockfunds and more effective on the use ofinventory resources.

inventory optimization; warehouse management; joint ordering; economic order quantity

2016-03-10

时兵兵(1990—)，男，硕士研究生，主要从事工业软件开发，E-mail:bing_share@163.com。

F416

A