一种鲁棒的基于射线跟踪的AOA目标定位算法

孔范增，李　洋，于海涛，郑娜娥

(1.解放军信息工程大学，河南 郑州 450001；2.北京石油化工学院 信息工程学院， 北京 102617)



一种鲁棒的基于射线跟踪的AOA目标定位算法

孔范增1，李洋2，于海涛2，郑娜娥1

(1.解放军信息工程大学，河南 郑州 450001；2.北京石油化工学院 信息工程学院， 北京 102617)

针对定位信号的多径传播和非视距噪声以及奇异方位线交点严重影响基于权值交点的AOA算法定位精度的问题，给出一种鲁棒的基于射线跟踪的AOA目标定位算法(RAOA-RT)。建立了微小区下的AOA定位模型，根据信号传播路径和镜像原理给出了镜像站的位置公式。所给RAOA-RT算法首先根据多径定位信号的跟踪结果构建镜像站，将NLOS径转化为到达镜像站的LOS径；其次，利用镜像站的AOA测量值形成相应的方位线，并获得所有方位线交点；最后，利用圆误差概率确定其中的有效交点，并依据有效交点的几何精度因子(GDOP)为其赋予相应的权值，对其进行加权求和作为目标的位置估计。仿真结果表明，与已有算法相比，RAOA-RT算法在不同应用场景下具有更高的定位精度，且其RMSE接近CRLB，鲁棒性更好。

定位；射线跟踪；到达角度(AOA)；几何精度因子;地理信息系统

在众多的定位技术中，基于射线跟踪的定位技术可有效解决基于距离的定位算法所面临的多径传播、可听见性和NLOS(Non Line of Sight)噪声等严重影响定位效果的问题而受到广泛关注[1]。

基于射线跟踪的定位技术综合利用多种定位信号的测量值实现对信号传播路径的跟踪，构建虚拟定位站，使其与目标之间具有直达径，以此为基础再运用各种基于距离的定位算法进行目标的位置解算。典型的基于距离的定位算法主要有到达时间(Time of Arrival，TOA)算法[3]、到达距离比算法[4]、到达时间差(Time Difference of Arrival，TDOA)算法[5]、基于时频差(Frequency Difference of Arrival，FDOA)算法[6]和到达角度(Angle of Arrival，AOA)算法[7]等，其中到达角度(AOA)算法是1个重要的研究分支。笔者主要研究基于射线跟踪的AOA定位算法及其克拉美罗下限(Cramér-Rao lower bound，CRLB)。

用于定位的射线跟踪已经有一些文献对其进行了研究。在只有一个反射面的条件下，基于多传感器实现对多径信号的直射和一次反射路径的跟踪[8]。基于多传感器，利用TOA和AOA的测量值以及几何约束关系设立虚拟传感器，完成对信号首达径的直射、反射和绕射的射线跟踪[9]。基于单传感器结合室内结构实现对多径信号传播路径的跟踪[10]。

基于AOA的定位算法，相关学者已经做了很多研究。Stansfield[11]提出一种加权最小二乘算法，文献[12]中提出一种具有闭式解的伪线性二乘算法。这2种算法都不需要目标位置的初始估计，且易于实现，但均是有偏估计，增加定位站不会彻底消除这个偏差。为消除估计偏差，先后提出了约束最小二乘[13]、总体最小二乘等算法，这些算法均是迭代算法，计算量较大。文献[14]中，证明了CLS算法和TLS算法是渐进最大似然估计。

文献[15]中给出1种最大似然估计算法，其在高斯条件下，可以最小化AOA整体测量误差，实现渐进无偏估计，算法性能接近CRLB。这些算法是迭代算法，需要1个比较接近目标真实位置的初始化位置，初始化位置不合理可能导致算法收敛于局部最优解或无法收敛[16]。

文献[18-22]中，利用传感器与目标的方位线两两之间的交点进行加权求和估计目标的位置，此类算法称为基于权值交点的AOA定位算法。文献[17]中提出了复合AOA(CAOA)算法，该算法将所有的方位线交点的均值作为目标的估计位置。文献[18]中提出了基于网格的和基于矢量的近似算法，这2种算法是迭代算法，计算量较大，且定位精度低于PLS算法。文献[19]中提出了基于敏感分析(SA)的定位算法，利用方位线交点的闭式解的一阶或二阶偏导定义各交点的敏感度，生成相应的权值，再进行加权求和。文献[20]中提出的基于CRLB权值交点的AOA(CWIAOA)定位算法，利用方位线交点的CRLB值得到交点的权值。CWIAOA算法定位精度均优于PLS算法，但没有考虑某些交点虽具有较大的权值，但其与目标真实位置之间的偏差却比权值较小的交点的偏差大，将这样的交点用于目标位置的估计会严重影响估计的精度，这样的交点可称为奇异方位线交点。

笔者首先根据定位站和目标所处微小区环境，建立了基于AOA的定位模型，包括信号传播环境模型和定位模型，并利用镜像原理给出镜像站的位置公式。其次，给出了1种鲁棒的基于射线跟踪的AOA目标定位算法(RAOA-RT)，该算法利用射线跟踪构建的镜像站及其AOA测量值，获得所有方位线交点，根据圆误差概率剔除奇异方位线交点，将剩余的方位线交点视为有效交点，对有效交点赋予相应的归一化权值并进行加权求和，完成对目标的位置估计。算法充分利用了定位信号的多径传播实现了单站定位，并且只对有效交点进行加权求和，在权值的计算中考虑了定位站的位置误差，使算法对应用环境具有较好的鲁棒性。算法仿真结果表明，该算法与CAOA、SA、CWIAOA等算法相比，在不同的应用场景下具有更好的适应性和定位精度。

1　微小区AOA定位模型

算法模型主要包括2部分：信号传播环境模型和定位模型。

1.1信号传播环境模型

对定位信号进行射线跟踪需要针对目标所在区域的地理信息构建无线信号传播的环境模型。该模型可通过实地测量或GIS系统获得。笔者所给算法主要用于微小区，故可假设目标所在区域的地面为水平的平坦地面。为简化模型，模型建立在二维平面内，建筑物的几何模型为其在地面上的投影所构成的多边形。多边形的边为建筑物的表面，且表面为光滑平面，射线在其上会发生反射，第i个表面可表示为：

(1)

两边的交点为建筑物表面相交的棱，射线到达棱时会发生绕射。

信号在传播过程中只发生直射或反射，由此构成的信号传播路径称为位置指向性路径(P-路径)，该信号称为位置指向性信号(P-信号)。P-信号在传播过程中发生N次反射，则称该信号为N阶P-信号，其传播路径称为N阶P-路径。第i条Ni阶P-路径表示为：

(2)

式中，Fi1，…，FiNi代表其经过的建筑物表面。

P-信号的传播路径通过反向跟踪算法是可以唯一确定的，路径的两端分别为定位站和目标。除直达径外，若信号的传播过程只存在反射，利用镜面反射原理，可以确定出镜像定位站，可以把非直达径转换为到达镜像定位站的直达径。为描述方便，直射信号也称为1阶P-信号，其传播路径称为1阶P-路径，其经过的平面为F0，此时定位站也称为镜像定位站。

1.2定位模型

定位站通过阵列天线接收多径定位信号，利用多重信号分类等算法实现对各径信号AOA的估计，并根据P-路径的跟踪结果转化为相应的镜像站的AOA估计。镜像站利用AOA估计值建立镜像站与目标之间的方位线，2条方位线的交点即为目标位置的粗估计值，对粗估计值进行加权求和可作为目标的位置估计。

(3)

(4)

式中，

另外，第i条P-路径为直达径，则Ai=I且Bi=0。

(5)

(6)

(7)

2　鲁棒的基于射线跟踪的AOA目标定位算法

在定位站完成对定位信号的射线跟踪的基础上，为提高AOA算法的定位精度，应剔除奇异方位线交点，消除其对目标位置估计的影响。为此引入圆误差概率(Circular Error Probable，CEP)解决这个问题。二维环境下圆误差概率的定义为定位结果落到以目标真实位置为中心的圆形区域C的概率。圆形区域C称为误差概率圆，他的半径定义为几何精度因子(geometric dilution of precision，GDOP)半径的n倍[21]，由式(8)确定，其中RCEP-P表示定位结果以概率P落入圆形区域C的半径。根据文献[21]，式(8)中P与n的关系可由式(9)确定，通过推导得到式(10)。

(8)

(9)

(10)

(11)

(12)

下面讨论GDOP的计算问题。在考虑镜像站的位置存在误差的情况下，根据式(7)对θi求全微分，得

(13)

得

(14)

利用伪逆求解目标的定位误差估计值为

(15)

(16)

(17)

根据式(5)，各镜像站的位置由定位站的位置和微小区的模型共同决定，假设定位站位置误差各元素之间互不相关，则

(18)

GDOP的计算方法既考虑了镜像站AOA测量误差，也考虑了镜像站的位置误差，具有较强的适应性。这里仍然以方位线i和方位线j的交点代替目标的真实位置，得到

(19)

(20)

(21)

(22)

(23)

(24)

根据式(23)、式(24)对各方位线交点进行加权求和，盲节点位置的估计值为

(25)

综上所述，本节所给的RAOA-RT算法主要包括以下几步：(1)获得镜像站的位置和AOA测量值；(2)得到方位线交点，确定有效交点；(3)对有效交点进行加权求和，获得目标的位置估计。RAOA-RT算法的具体步骤如表1所示。

表1　RAOA-RT算法步骤

3　CRLB

其CRLB矩阵为C=J-1，则算法的CRLB可由CRLB矩阵的迹求得：

(26)

4　仿真结果与分析

为验证所给算法的性能，在2种典型场景下对RAOA-RT算法、CAOA算法、CWIAOA算法和SA算法的定位性能进行比较。在每个场景下，每种算法进行1000次Monte-Carlo仿真，统计算法的均方根误差(Root Mean Square Error，RMSE)。在场景1下建筑物位于目标的一侧，定位站由此产生的镜像站位于目标的一侧。场景2下目标被建筑物包围，定位站由此产生的镜像站位于目标的周围。因此可比较镜像站不同分布方式对算法定位性能的影响。

场景1：微小区1内存在3个建筑物，建筑物在水平面的投影坐标如表2所示。定位站真实坐标为(0，45)，目标真实坐标为(250，40)，定位站已知位置在x轴和y轴方向存在误差nx0和ny0，其服从零均值正太分布，标准差为σx0=σy0=σs=2，且互不相关。在定位站与目标之间有4条1阶P-路径，即存在4个镜像站(表3)，如图 1所示。假设射线跟踪算法可正确跟踪所有P-路径，即跟踪结果所经过建筑物表面与实际路径经过的建筑物表面一致。镜像站AOA测量误差服从零均值高斯分布，标准差为σ1=…=σ4=σθ，且互不相关，σθ的取值范围为[1°，5°]。

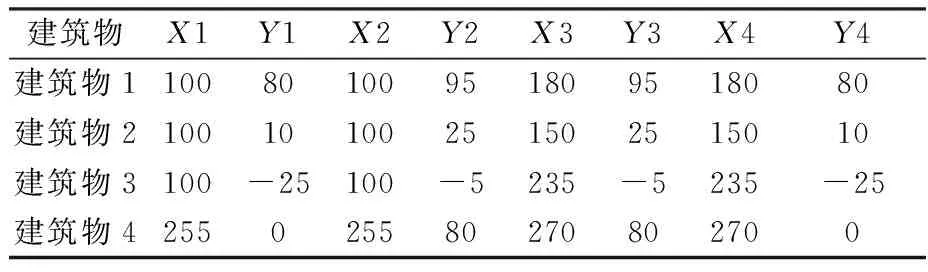
表2　微小区1和微小区2内建筑物坐标

表3　微小区1和微小区2内镜像站坐标

场景1下各算法的RMSE随σθ变化的曲线如图 2所示。从图2中可以看出，在场景1下，CAOA算法的性能最差，RAOA-RT算法的整体性能优于其他算法，CAOA和SA算法的RMSE偏离CRLB的程度随σθ的增加而明显增大。当σθ<3.5°时，RAOA-RT算法与CWIAOA算法的性能相近，但当σθ>3.5°时，CWIAOA算法的RMSE明显偏离CRLB。

场景2：微小区2内存在4个建筑物，建筑物在水平面的投影坐标如表2所示。定位站真实坐标为(0，45)，目标真实坐标为(250，40)，定位站已知位置在x轴和y轴方向存在误差nx0和ny0，其服从零均值正太分布，标准差为σx0=σy0=σs=2，且互不相关。在定位站与目标之间有5条1阶P-路径和3条2阶P-路径，存在8个镜像站(表3)，如图 3所示。假设射线跟踪算法可正确跟踪所有P-路径。镜像站的AOA测量误差服从零均值高斯分布，标准差为σ1=…=σ8=σθ，且互不相关，σθ的取值范围为[1°，5°]。

场景2下各算法的RMSE随σθ变化的曲线如图 4所示。从图 4中可以看出，在场景2下，CAOA算法的性能最差，SA算法的性能好于CAOA算法，RAOA-RT算法的性能优于其他算法。当σθ<3°时，RAOA-RT算法和CWIAOA算法性能接近；当σθ>3°，RAOA-RT算法的性能优于CWIAOA算法。

对比场景1与场景2可以发现，上述几种算法在场景2下的定位性能比在场景1下的性能相对要好，即镜像站分布目标周围时，算法的定位性能比较好。

仿真结果表明，所给RAOA-RT算法在不同仿真场景下较其他几种算法有更好的适应性，且该算法的定位精度在整体上优于其他算法。

5　结束语

给出了一种鲁棒的基于射线跟踪的AOA目标定位算法。算法的核心思想是定位站根据多径定位信号的相关测量值实现射线跟踪并构造镜像站，将NLOS径转化为LOS径，生成相应的方向线并获得方位线交点，利用圆误差概率在所有的方位线交点中确定有效交点，根据有效交点的GDOP为其赋予相应的权值，并对有效交点进行加权求和，得到目标的位置估计。RAOA-RT算法充分利用了定位信号的多径传播，在GDOP的计算中考虑了定位站位置的误差对计算结果的影响，且不需要初始值进行迭代，且可以为其他定位算法提供更加合理的初始值。仿真结果表明，RAOA-RT算法与CWIAOA算法、SA算法和CAOA算法相比，具有更好的适应性，且算法的整体定位精度更高。

[1]周晓平，谭凤杰，柳朝阳，等.射线跟踪技术场强计算的改进算法[J].电波科学学报，2013，28(4):669-675．

[2]袁正午.蜂窝通信系统移动终端射线跟踪定位理论与方法研究[D].长沙：中南大学，2003．

[3]朱国辉，冯大政，周延，等.一种线性校正TOA定位算法[J].西安电子科技大学学报，2015，42(3)：22-25．

[4]郝本建，李赞，万鹏武，等.传感器网络基于特征值分解的信号被动定位技术[J].物理学报，2014(5):54304-054304．

[5]Compagnoni M， Notari R. TDOA—based localization in two dimensions: the bifurcation curve[J]. Fundamenta Informaticae， 2014，135：199-210．

[6]逯志宇，王大鸣，王建辉，等.基于时频差的正交容积卡尔曼滤波跟踪算法[J].物理学报，2015，64(15):150502-150502．

[7]Shao H J， Zhang X P， Wang Z. Efficient closed-form algorithms for AOA based self-localization of sensor nodes using auxiliary variables[J]. IEEE Transactions on Signal Processing， 2014，62(10):2580-2594．

[8]Lui K W K， So H C. Range-based source localication with pure reflector in presence of multipath propagation[J]. Electronics Letters， 2010，46(8):957-958．

[9]Liu D L. Joint TOA and DOA localization in indoor environment using virtual station[J]. IEEE Communications Letters， 2014，18(8):1423-1426．

[10]Setlur P， Smith G E， Ahmad F， et al. Target localization with a single sensor via multipath exploitation[J]. IEEE Transactions on Aerospace and Electronic Systems， 2012，48(3):1996-2014．

[11]Stansfield R. Statistical theory of d.f. fixing[J]. Journal of the Institution of Electrical Engineers-Part IIIA: Radiocommunication， 1947，94(15):762-770．

[12]Pages-Zamora A， Vidal J， Brooks D H. Closed-form solution for positioning based on angle of arrival measurements[C]∥the 13th IEEE International Symposium on Personal， Indoor and Mobile Radio Communications. Lisboa， Portuga， 2002:1522-1526．

[13]Ho K， Chan Y. An asymptotically unbiased estimator for bearingsonly and doppler-bearing target motion analysis[J]. IEEE Transactions on Signal Processing， 2006，54(3):809-822．

[14]Gu G. A novel power-bearing approach and asymptotically optimum estimator for target motion analysis[C]∥the IEEE Conference on Decision and Control， Atlanta， Georgia， USA， 2010:5013-5018．

[15]Wang Z， Luo J A， Zhang X P. A novel location-penalized maximum likelihood estimator for bearing-only target localization[J]. IEEE Transactions on Signal Processing， 2012，60(12):6166-6181．

[16]Le Cadre J P， Jaetffret C. On the convergence of iterative methods for bearings-only tracking[J]. IEEE Transactions on Aerospace and Electronic Systems， 1999，35(3):801-818．

[17]Brida P， Machaj J， Benikovsky J， et al. A new complex angle of arrival location method for ad hoc networks[C]∥the 7th Workshop on Positioning Navigation and Communication， Dresden， Germany，2010:284-290．

[18]Jiang J R， Lin C M， Hsu Y J. Localization with rotatable directional antennas for wireless sensor networks[C]∥the 39th International Conference on Parallel Processing Workshops， San Diego， California， USA， 2010:542-548.

[19]Pezeshk A A M， Dallai M. A novel method for position finding of stationary targets using bearing measurements[C]∥the C4I Conference at Sharif University of Technology， 2010．

[20]Duan Z， Zhou Q. CRLB-weighted intersection method for target localization using AOA measurements[C]∥Computational Intelligence and Virtual Environments for Measurement Systems and Applications (CIVEMSA)， Shenzhen， China， 2015．

[21]Yu K G，Sharp I， Guo Y J.地面无线定位技术[M].北京：电子工业出版社，2012:178-180．

A Robust AOA Target Localization Method Based on Ray Trace

KONG Fan-zeng1, LI Yang2, YU Hai-tao2， ZHENG Nae1

(1.The PLA Information Engineering University, Zhengzhou 450001, China; 2.Journal of Beijing Institute of Petro-Chemical Technology, Beijing 102617, China)

Multipathpropagation and non-line of sight (NLOS) propagation of positioning signal, and singular bearing line intersection, seriously influence the positioning accuracy of weighted intersection methods for target localization using AOA(Angle of Arrival) measurements. In this paper, a method called robust AOA target localization method based on ray trace (RAOA-RT) is proposed. We establish the AOA localization modelin microcell. We get the position formula of the image base stations (IBS) according to ray-tracing result of multipath positioning signal and the principle of mirror image. The proposed RAOA-RT method firstly constructs IBSs according to ray-tracing result of multipath positioning signal, and transforms the NLOS path to LOS path arriving at the IBS. Secondly, the method establishes bearing lines between the IBSs and the target by the AOA measurements at the IBSs, and gets all the intersections of bearing lines (IBL). Finally, the effective IBLs are determined by circular error probable and distance between the IBLs. We can give the reasonable weight of every effective IBLs based on their geometric dilution of precision (GDOP), and get an accurate estimate of target position by weighted merge all the effective IBLs of bearing lines. The simulation results show that RAOA-RT method is more accurate than other methods, and the RMSE of RAOA-RT method is much closed to the CRLB, and RAOA-RT method has better robustness in different application scenarios.

positioning; ray tracing; angle of arrival (AOA); geometric dilution of precision (GDOP); geographic information system (GIS)

2016-03-18

孔范增(1982—)，硕士，研究方向为无线定位技术及能信协议分析，E-mail:kfz821118@163.com。

TN92

A