轻型机械臂的轻量化结构设计优化方法
2016-10-19杨世强王蓓蓓
杨世强 王蓓蓓,2
1.西安理工大学,西安,710048 2.西安飞豹科技发展公司,西安,710089
轻型机械臂的轻量化结构设计优化方法
杨世强1王蓓蓓1,2
1.西安理工大学,西安,7100482.西安飞豹科技发展公司,西安,710089
在轮式移动机器人基础上,开发移动机械臂,设计了一种轻型五自由度机械臂,建立了三维实体模型,以减轻机械臂自身质量为目标,对关键构件进行了减重孔方案设计和结构优化,利用有限元方法计算得到了在不同载荷下不同方案的应力应变规律、模态与振型,对比分析了不同减重方案的优劣性,给出了最优减重方案,为机械臂结构设计提供了理论依据。
移动机械臂;有限元分析;结构优化;减重方案
0 引言
随着机器人技术的迅速发展,机器人在生产、日常生活等方面凸显出越来越明显的重要性和优越性,成为研究复杂智能行为、探索人类思维模式的有效工具与实验平台[1-2]。移动机械臂系统是由一个或多个自由度的机械臂固定在移动平台上构成的特殊移动机器人系统,通过引入平台的移动,拓展了机械臂的工作空间,使得移动机械臂系统优于移动机器人和传统的机械臂[2-5]。作为移动机械臂系统中的重要部分之一,机械臂一直是研究的重点[6],有限元分析应用于机械臂结构部件的研发和设计中,特别是机械臂的振动分析,大大缩短了产品的开发周期,降低了研发成本[7]。
本研究在现有轮式自主移动机器人基础上研发设计了轻型机械臂,构成移动机械臂,将三维建模软件和有限元分析结合,为减小移动机械臂的手臂自身质量,进行了手臂结构设计与优化,分析了结构设计优化方案的合理性。
1 机械臂系统模型
移动机械臂由轮式自主移动机器人和机械臂两部分组成, 移动机器人完成大范围移动,而机械臂实现小范围、灵活、准确的复杂运动,从而构成人形移动机器人系统。图1a所示的五自由度串联机械臂固定在图1b所示的现有轮式移动机器人肩部之上,构成图1c所示的移动机械臂。五自由度机械臂由可回转的腰关节、可俯仰的肩关节、肘关节、可回转和俯仰的腕关节构成,图中1为机械臂安装基座,固定于移动机器人肩部,2、4、6、8、10均为回转关节(驱动元件已去除),3、5、7、9均为连接关节的构件。机械臂伸展长度为390 mm,额定载荷为7 N,机械臂自重与负载的总重不大于70 N。各主要构件的三维实体模型如图2所示。
机械臂是一个典型的悬臂梁结构,自身质量对机械臂有重要影响,在轮式移动机器人额定载荷一定的情况下,如何减小机械臂质量,同时满足刚度和动态性能要求是机械臂设计研究的重要内容,可通过设计合理的构件模型和选择合适的构件材料两方面来实现轻量化。

(a)机械臂实体模型图
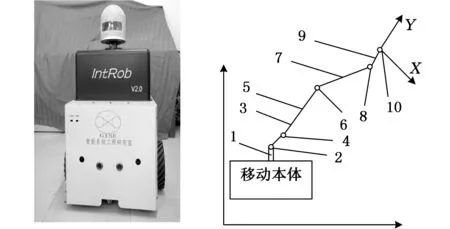
(b)轮式移动机器人 (c)移动机械臂运动简图1.机械臂安装基座 2,4,6,8,10.回旋关节3,5,7,9.关节连接构件图1 机械臂系统模型图
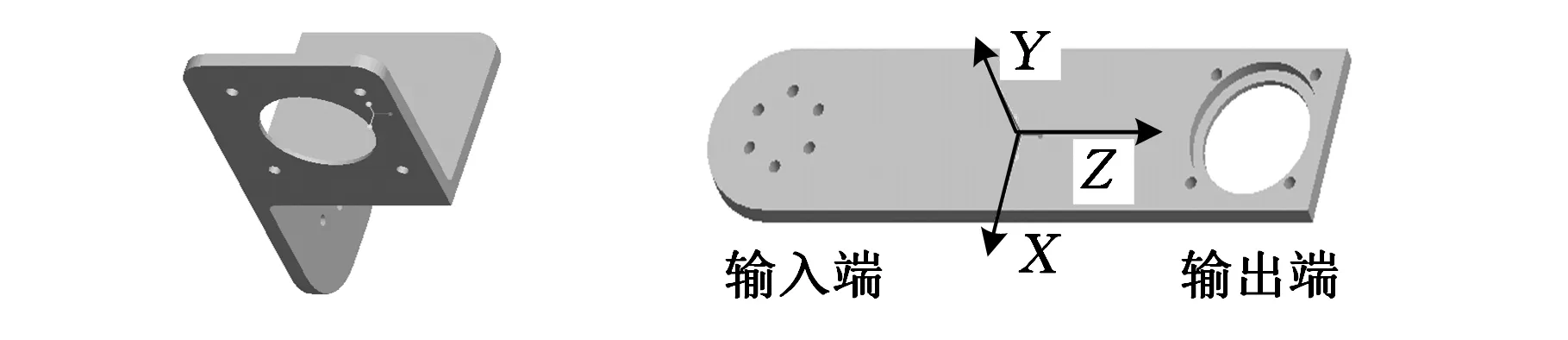
(a) 构件3 (b)构件5

(c)构件7 (d)构件9 图2 机械臂构件三维实体模型
在设计机械臂的构型时,根据机械臂运动空间以及现有轮式移动机器人的参数要求可以初步确定机械臂系统中肩关节构件3的宽度尺寸与基座的端面宽度相等,腕关节构件9的宽度与小臂构件7端面宽度相等。构件3和构件9尺寸较小,可以用微缩的直角型板材代替。构件5和构件7长度均为230 mm,构件5带有70 mm直角弯头,它们的参数决定了机械臂运动范围的半径,其质量所占整个机械臂质量的比重大,其尺寸参数和质量在很大程度上影响机械臂的总体尺寸和质量,优化构件5和构件7具有重要意义。
在满足刚度与强度条件下,为尽可能减小机械臂质量,机械臂的各关节采用5个规格不同、集成度高、质量较小的自带减速器的AC伺服单元[8]驱动,各零件材料的选择影响机械臂工作的安全性和可靠性,铝合金具有密度小、加工性能和导热性好等优点,机械臂材料采用厚度为6 mm、宽度为60 mm的铝合金材料6061T板材。
2 减重孔方案设计
为了有效减小机械臂质量,满足整个移动机械臂系统的设计需求,对机械臂进行受力分析,在满足机械性能要求以及材料许用性能的前提下,需设计选择合适的轻量化方案。对于机械臂系统依次从腕关节(8-10)、小臂(7)、肘关节(6)、大臂(5)、肩关节(4)分别标记为第i个构件,第i个构件载荷Fi为
(1)
式中,m为末端执行器(含额定载荷)质量;Mj为第j个关节或构件质量;g为重力加速度。
由式(1)得构件7末端载荷为20N,对构件7添加约束,固定输入端X、Y、Z三个方向的转动和平动,输出端电机安装处等效为四个接触点[9],每个接触点平均载荷为5N。对构件7的四个接触点在X、Y、Z三个方向(坐标系已在图2标明)分别施加大小为6N的载荷,各方向的应力云图和应变云图如图3所示。

(a)X方向应力云图
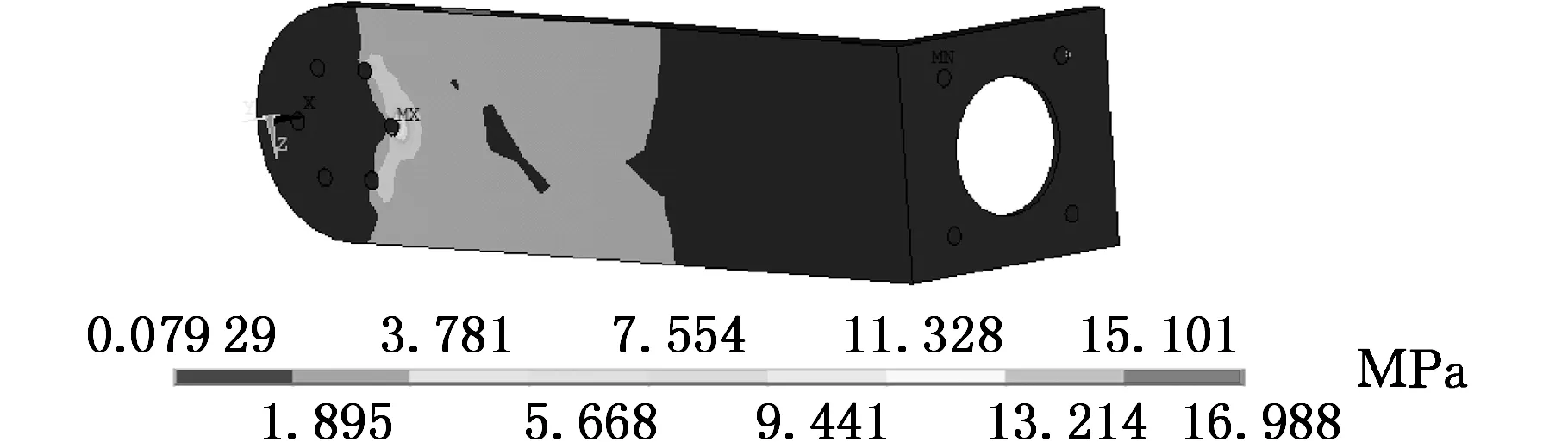
(b)Y方向应力云图

(c)Z方向应力云图

(d)X方向应变云图

(e)Y方向应变云图

(f)Z方向应变云图图3 构件7施加6 N载荷下应力应变云图
由图3看出在受到同样大小的作用力时,在Y方向的应力应变最大,X方向次之,Z方向最小,应力应变分布不均匀,应力集中明显。因此对Z方向进行结构优化,得到骨性结构,施加6N载荷,其应力应变云图如图4所示。
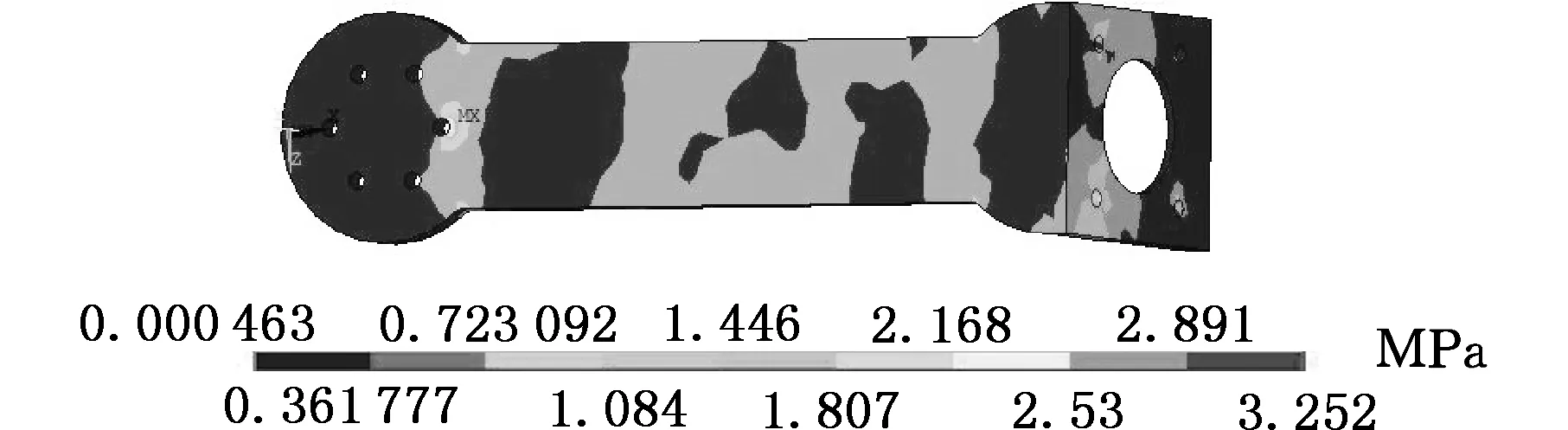
(a)X方向应力云图

(b)Y方向应力云图

(c)Z方向应力云图

(d)X方向应变云图
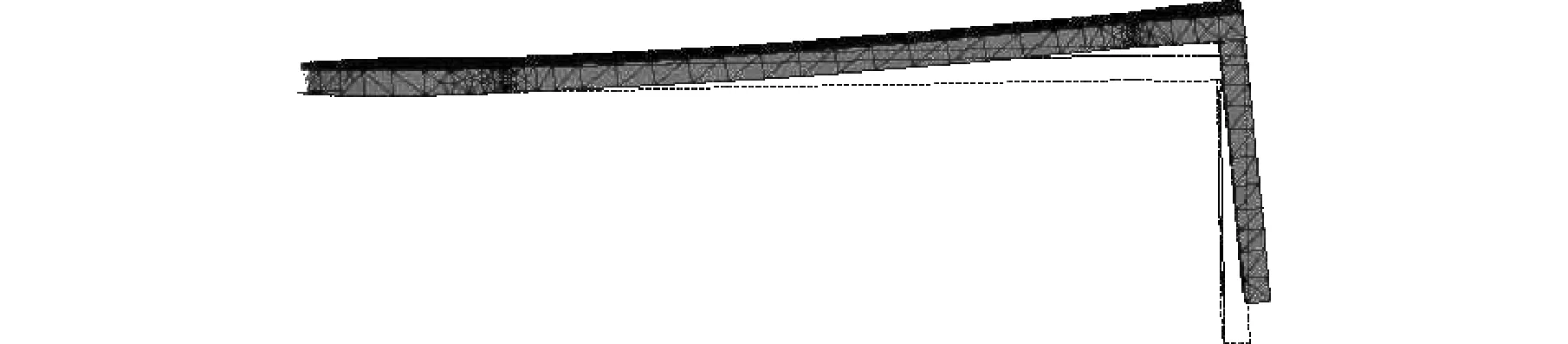
(e)Y方向应变云图

(f)Z方向应变云图图4 构件7结构优化后施加6 N载荷下应力应变云图
由图4可以看出,对机械臂进行Z方向结构优化后,机械臂构件的质量仍然较大,构件有进一步减重优化的空间。为了更进一步减小质量,采用增加减重孔的方式优化结构。当减重孔去除面积相同时,剩余面积相同,机械臂质量相同,所以“寻找质量最优”的问题就转化为“寻找减重孔最优”问题。减重孔的面积一定时,为了研究减重孔的布置形式和位置对构件力学性能的影响,分别建立模型0~模型7,其中模型0为类梯形减重孔,模型1是具有5个大小相等的圆形减重孔,模型2和模型3是具有12个大小相等、分布不同的圆形减重孔,模型4和模型5是具有15个大小相等、分布不同的圆形减重孔,模型6和模型7是具有18个大小相等、分布不同的圆形减重孔,如图5所示。

(a)模型0(b) 模型1

(c)模型2(d) 模型3

(e)模型4(f) 模型5

(g)模型6(h) 模型7
图5模型0~模型7减重孔截面图
在材料和施加载荷一致、去除面积一致的条件下,分别对以上模型在ANSYS环境下进行静力学分析,提取应力和变形量的最大值,绘制曲线图如图6所示。其中X、Y、Z分别表示X、Y、Z方向施加6N载荷时的应力、应变值。
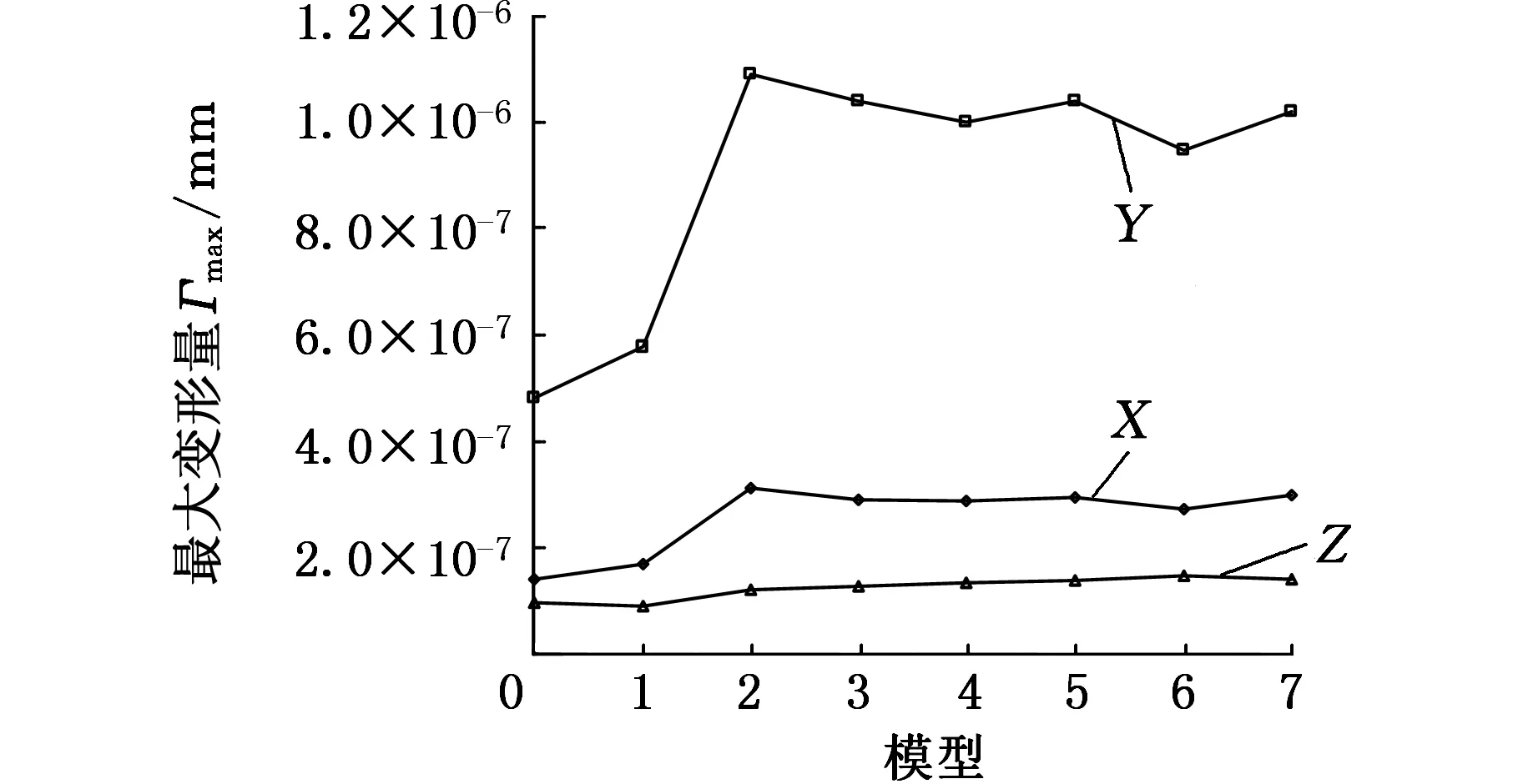
(a)最大变形量

(b)最大应力图6 6 N载荷下X、Y、Z向应力和变形量最大值
从计算结果可以看出,在载荷和去除面积相等的情况下,各减重方案具有以下特征:
(1)减重孔的存在会改变构件的刚度、强度等性能,对构件的力学性能产生不同影响;
(2)减重孔的数量、位置及排列方案对构件的力学性能有显著影响,应力与应变的最大值不同;
(3)相同条件下,类梯形孔的模型0系列在X和Y方向的应力、应变均最小,且与材料最大许用值有一定差距,即以上各减重方案中,类梯形孔的减重方案与其他各减重孔方案相比更具有优越性,可以进一步优化。
3 减重孔方案优化
进一步优化构件7的模型0系列板模型截面,如图7所示,减重孔面积S1为
(2)

图7 构件7的模型0系列模型截面
在确定其对称性的前提下,对于构件7,c=14mm、d=20mm、l=230mm、m=60mm不变,由式(2) 可以看出、S1与b线性相关,即随着b的增加,减重孔的面积增加,机械臂的质量减小。当a=50mm,即减重孔的位置一定时最大应力应变随着b的变化规律如图8所示。可以看出,当a为定值,b=30mm时应变最小,且应力在材料许用范围内。

(a)最大变形量
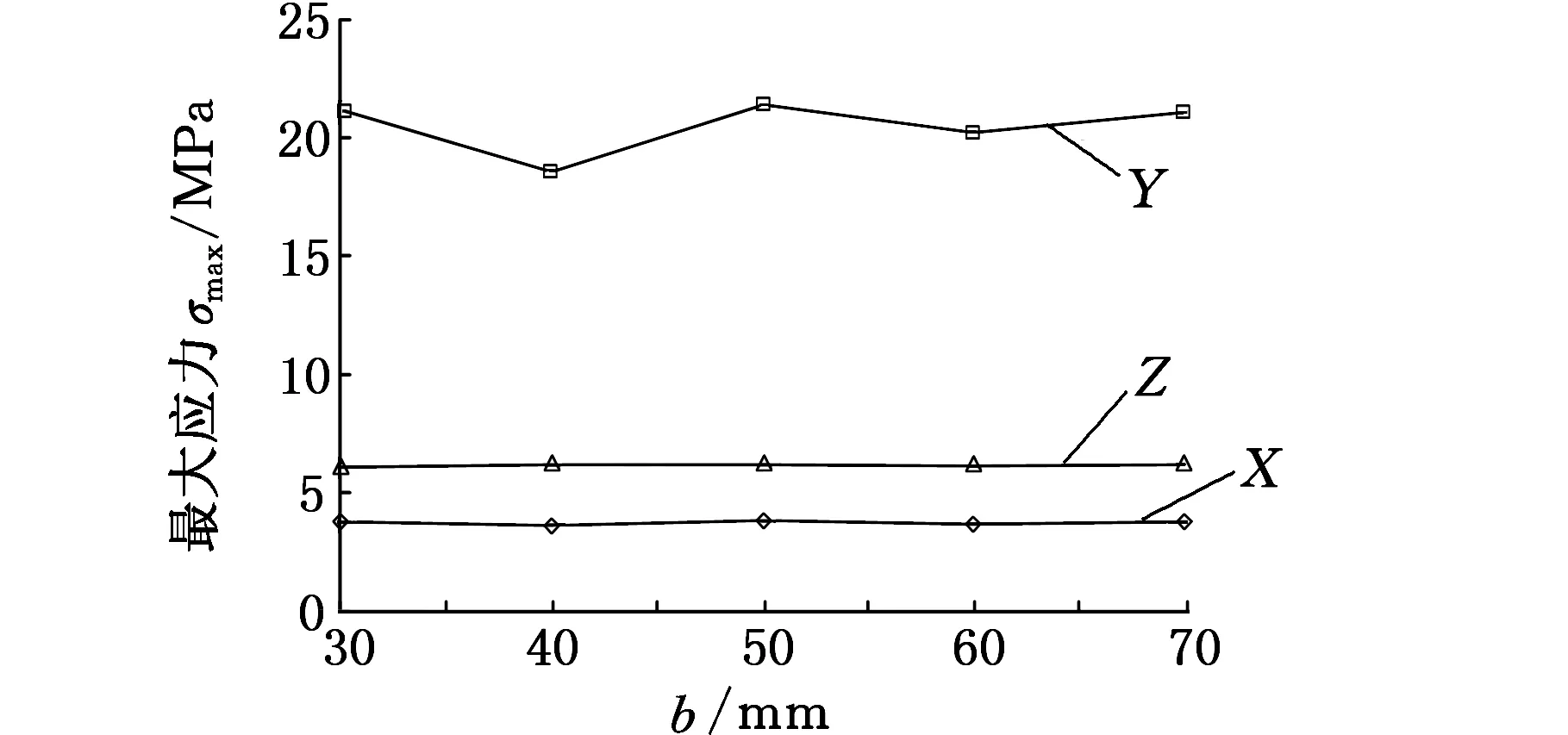
(b)最大应力图8 6 N载荷下,参数a固定时,参数b变化引起的最大应力和变形量的变化
当b=30mm,即减重孔的面积一定时,最大应力应变随着a的变化规律如图9所示。可以看

(a)最大变形量
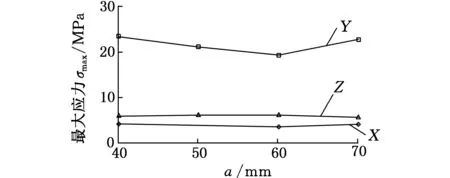
(b)最大应力图9 6 N载荷下,参数b固定时,参数a变化引起的最大应力和变形量的变化
出,当b=30mm为定值时,a=50mm时应力应变都相对较小。
由图9可以看出,当b=30mm时,等载荷下应力随着a的变化先变小,后变大,在a=60mm时较小,而应变则在a=50mm时相对较小。
综合考虑应变变化规律、应力最大值与分布状况,以及两者对机械臂性能的影响,可以看出减重面积一定时,可以找到相对较优的减重孔位置。结合减重孔位置一定时,面积变化对应力应变的影响规律,可以看出,模型0(a=50mm,b=30mm)在等面积情况下应力分布相对均匀,最大的应力应变值相比于其他模型较小,且未超过材料许用值;随着载荷增加,最大应力应变增加趋势良好,应变特征相对最优。


图10 构件5的模型0系列模型截面
在对称结构的前提下,当a+b=42mm,选取a分别为18,17,16,15,14,13,12,11mm,得到A~H八种模型,添加四组减重孔为圆形的减重方案,分别表示为T1(5孔)、T2(8孔)、T3(9孔)和T4(10孔),加8N的载荷,最大应力应变如图11所示,由图11可以看出,T1~T4应力和应变均明显较大,不宜采用,在此主要分析讨论A~H八种类型。

(a)最大变形量

(b)最大应力图11 8 N等载荷条件下应力和变形量曲线
同类型条件下不同载荷引起的机械臂应力应变如图12所示。

(a)最大变形量

(b)最大应力图12 模型E的变形量和应力曲线
结合图11和图12,可以得出以下结论:
(1)从应变方面来看,在X、Y、Z三个方向,模型E都显示出较好特征。8N载荷下各个模型在三个方向的应变变化都较平稳,随着载荷的增加,应变出现波动,而模型E在应变方面对载荷的变化相对最不敏感,在等载荷条件下应变都最小,有很明显的优势。
(2)从应力方面来看,模型E也显示出较好特征,等质量全圆形减重孔在相同载荷下的应力分布除X方向较稳定以外,其余方向应力较大且分布不均匀,特别是在应力整体相对较大的Y方向。
(3)模型E在应变方面显示出较好的特征,在等载荷条件下应变最小。应力方面,在X方向,应力的最大值随载荷增加而增加,Y方向也满足材料许用条件。构件5的类梯形模型E减重孔方案在额定载荷至1.625倍载荷区间内,应力应变最小,且满足材料的许用要求。
4 移动机械臂构件动态分析
4.1动态响应分析
将动态载荷施加到构件上,分析构件在受到动态载荷时的应力应变值,对构件7和构件5的相对较优模型施加动态正弦载荷F(t)=Fnsinωt,n=1,2,ω=π/6,Fn分别为构件5和构件7静态极限载荷,F1=13N,F2=10N,Y方向应力最大,其最大应力如图13所示,从图13所示的计算结果可以看出,构件7和构件5在受到动态外部激励时会产生内部应力,最大应力分别为51.70MPa和50.52MPa,均在材料的许用应力范围内。
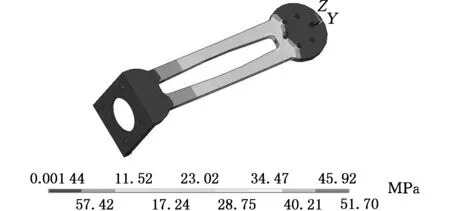
(a)构件7应力云图

(b) 构件5应力云图图13 构件7和构件5应力云图
4.2模态分析
对机械臂进行模态分析,了解其具有的固有频率和振型,避免在使用中产生共振,模态分析是振动特性分析的核心,是研究结构动力学中一种极为重要的分析方法,利用模态分析可以分析观察及确定机械臂的振动特性,即固有频率和多阶振型。
对构件5、构件7模型进行模态分析,前5阶固有频率如图14、图15所示。

图14 构件5前5阶固有频率变化图
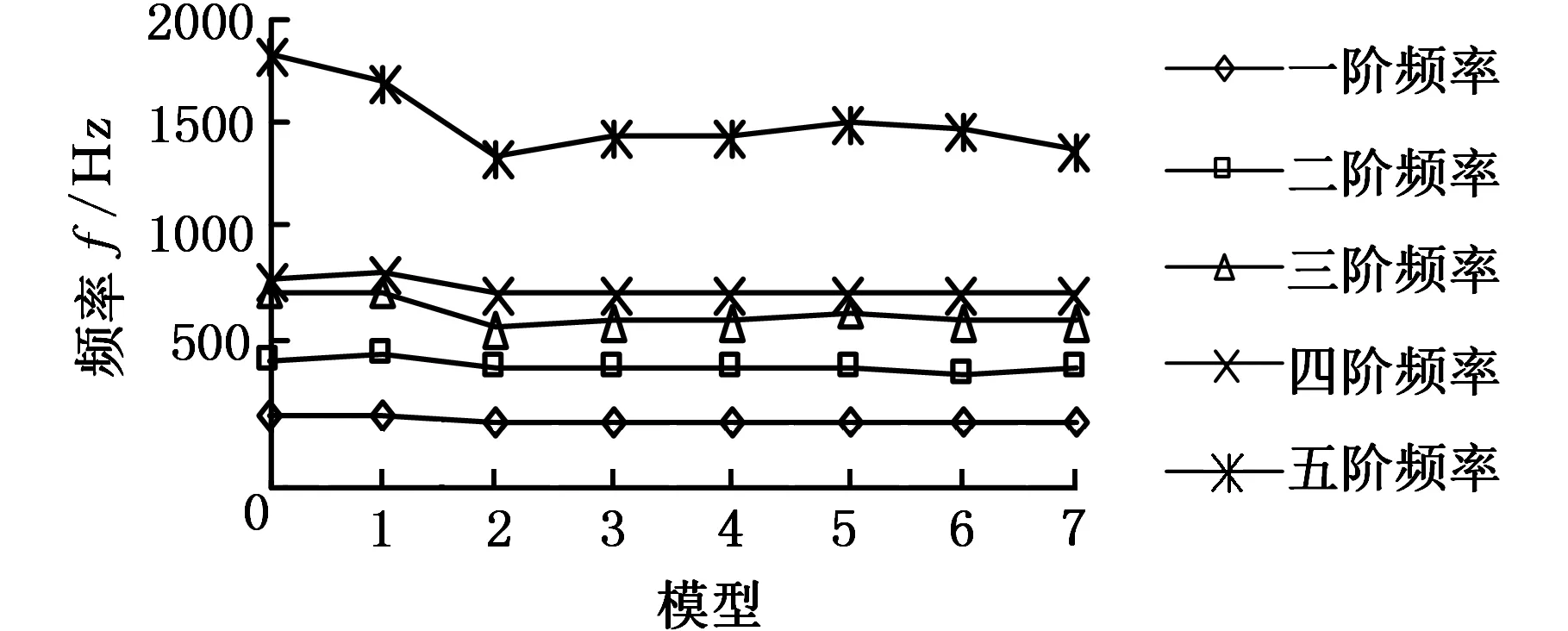
图15 构件7前5阶固有频率变化图
由以上两图可以看出,由于圆形减重孔与类梯形减重孔的截面形状不同,结构的不同引起结构内部的变化不同,模型A~H类梯形孔各阶频率变化规律不同,各阶频率都相对于0系列模型较大,减重孔的存在使构件固有频率均有所下降。
图16和图17显示了构件7和5的1~5阶振型,其中灰色部分为机械臂静态状态,深色部分为各阶振型,总结构件5与构件7的前5阶固有频率及其振型如表1所示。

(a)1阶振型 (b)2阶振型

(c)3阶振型 (d)4阶振型

(e)5阶振型图16 构件7前5阶振型图
可以看出,两构件的一阶振型均为绕X轴的弯曲,二阶振型不同,构件5的二阶振型为绕Y轴的弯曲,而构件7的二阶振型为绕Z轴的扭转,三阶及更高阶振型互不相同,但均为弯扭耦合的复合振型。

(a)1阶振型 (b)2阶振型

(c)3阶振型 (d)4阶振型

(e)5阶振型图17 构件5前5阶振型图
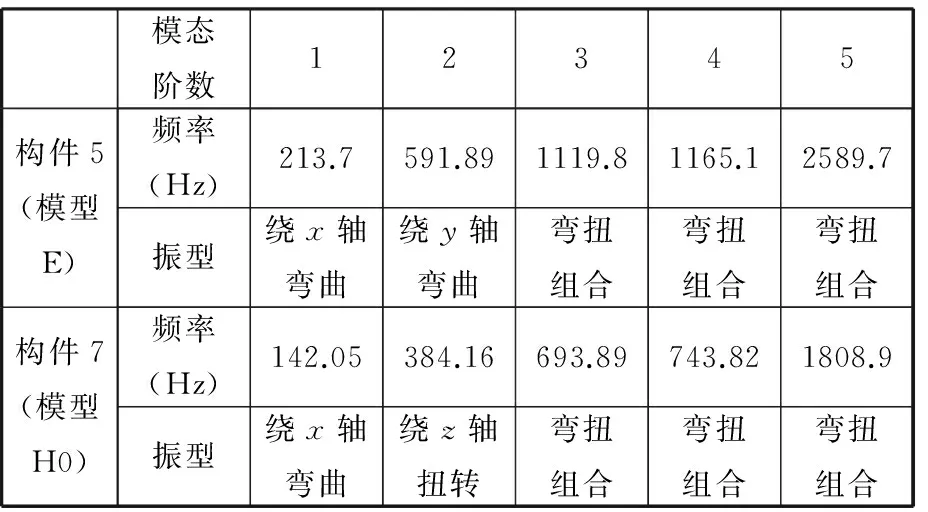
模态阶数12345构件5(模型E)频率(Hz)213.7591.891119.81165.12589.7振型绕x轴弯曲绕y轴弯曲弯扭组合弯扭组合弯扭组合构件7(模型H0)频率(Hz)142.05384.16693.89743.821808.9振型绕x轴弯曲绕z轴扭转弯扭组合弯扭组合弯扭组合
模态分析计算结果表明,构件5和构件7的各阶频率较高,均远离机械臂工作频率,不会产生共振。
5 结语
在分析移动机械臂系统需求的基础上,建立了轻型移动机械臂系统实体模型,对机械臂系统中关键的两个构件进行了静力学分析,为减小机械臂的质量,对主要构件设计了不同轻量化方案,对比分析了不同方案的应力应变变化规律,得到了较优方案,对其进行模态分析,计算结果表明给出的最终方案可以满足所设计的机械臂性能要求。
[1]SephenS,DavidG.Lowe,JamesJ.Little.Vision-basedGlobalLocalizationandMappingforMobileRobots[J].Robotics,IEEETransactionson, 2005,21(3): 364-375.
[2]杜滨. 全方位移动机械臂协调规划与控制[D]. 北京:北京工业大学,2013
[3]于登云, 孙京, 马兴瑞. 空间机械臂技术及发展建议[J] . 航天器工程, 2007, 16(4):1-9.
Yu Dengyun,Sun Jing,Ma Xingrui. Suggestion on Development of Chinese Space Manipulator Technology[J]. Spacecraft Engineering, 2007, 16(4):1-9.
[4]张波涛.移动机械臂运动规划算法及其应用研究[D]. 上海:华东理工大学,2012.
[5]Sheng Lin.Robust and Intelligent Control of Mobile Manipulators[D].Toronto:University of Toronto,2001.
[6]吴玉香,胡跃明.二阶动态滑模控制在移动机械臂输出跟踪中的应用[J].控制理论与应用,2006,23(3):410-416.
Wu Yuxiang, Hu Yueming. Second Order Dynami-cal Sliding Mode Control and Its Application to Output Tracking of Mobile Manipulators[J].Control Theory & Applications,2006,23(3):410-416.
[7]田野,陈晓鹏,贾东永,等.仿人机器人轻型高刚性手臂设计及运动学分析[J].机器人,2011,33(3):332-339
Tian Ye, Chen Xiaopeng, Jia Dongyong,et al. Design and Kinematic Analysis of a Light Weight and High Stiffness Manipulator for Humanoid Robots[J].Robot,2011,33(3):332-339.
[8]哈默纳克有限公司.谐波传动[EB/OL].[2015-04-08]http://www.harmonicdrive.net.cn/xuanz/sfzxyj 2.shtml.
[9]王高利, 唐吉运.全尺寸飞机结构试验约束点载荷误差分析及优化[J].工程与试验,2014,54(2):42-45.
Wang Gaoli,Tang Jiyun. Error Analysis & Optimization of Full Aircraft Test[J].Engineering &Test,2014,54(2):42-45.
(编辑华中平)
Lightweight Structure Design and Optimization Method for a Light Mobile Manipulator
Yang Shiqiang1Wang Beibei1,2
1.Xi’an University of Technology,Xi’an,710048 2.Xi’an Feibao Development Company,Xi’an,710089
A mobile manipulator was presented based on the original mobile robot. A light weight manipulator with 5-DOF was presented and its 3D solid model was constructed. The lightening schemes of the key parts were presented to reduce the whole weight of the manipulator and the structure was optimized. The rules of stress and strain to the key parts with different lightening schemes under different loads were provided by finite element method, and the modals and vibration modes of the key parts were obtained as well. The advantages and disadvantages among different lightening schemes were contrasted, and the best lightening scheme was given. The theoretical basis for the optimization of the manipulator structure design was shown.
mobile manipulator; finite element analysis; structure optimization; lightening scheme
2015-11-11
国家自然科学基金资助项目(51475365);陕西省教育厅省级重点实验室科学研究计划资助项目(12JS071);陕西省教育厅科学研究计划资助项目(2013JK1000)
TP242.6;TH114
10.3969/j.issn.1004-132X.2016.19.004
杨世强,男,1973年生。西安理工大学机械与精密仪器工程学院副教授。主要研究方向为智能机器人控制。发表论文20余篇。王蓓蓓,女,1989年生。西安理工大学机械与精密仪器工程学院硕士研究生。
