面齿轮磨削加工工艺参数的优化

明兴祖　罗　旦　刘金华　严宏志

1.湖南工业大学，株洲，412007　　2.中南大学，长沙，410083



面齿轮磨削加工工艺参数的优化

明兴祖1罗旦1刘金华1严宏志2

1.湖南工业大学，株洲，4120072.中南大学，长沙，410083

基于磨削面齿轮工艺参数的分析，在满足产品质量要求和磨削加工条件等设计约束的前提下，建立了以磨齿效率和表面质量为目标函数的多目标优化数学模型。将内点罚函数法与遗传算法相结合用于该数学模型的优化计算，获得了三组最优的磨削用量方案且三组方案均能使磨齿效率和表面质量得到较大提高。根据优化后的结果设计并完成了工艺实验，实验结果也验证了该方法的正确性、有效性和实用性。

面齿轮；磨削；工艺参数；多目标优化；内点罚函数法；遗传算法

0　引 言

面齿轮传动是一种圆柱齿轮与圆锥齿轮相啮合的齿轮传动,它具有诸多优点和几何特性[1]。磨削一般作为面齿轮的最终加工工序，因其成形机理复杂，影响加工因素多，加工参数在线检测困难，所以磨削加工过程的工艺方案优选是困扰制造企业的难题[2-3]。为实现高质量、高精度、高效率、低耗能的加工目标，需研究各个磨削工艺参数对加工目标的影响规律，找出最佳的工艺参数值，确定优化的工艺方案。

在工艺参数优化研究方面，国内外学者已进行了大量研究。Venkata等[4]为获取最高生产率，采用了多种进化算法对多道铣削的工艺参数进行优化。Yildiz[5]以生产成本最低为目标函数，提出了一种田口-差分进化混合优化算法，实现了多道车削加工过程中的工艺参数优化。Savadamuthu等[6]采用遗传算法对车削过程的工艺参数进行了优化。Ho等[7]将正交试验与遗传算法相结合，以表面粗糙度为研究目标，使表面粗糙度的预报误差达到4.06%。以上文献虽均采用进化算法进行求解，但不足之处在于仅考虑单目标函数，没有综合考虑更多的优化目标。在面齿轮磨削工艺参数优化程中，需考虑使加工质量和加工效率在给定条件下尽可能最佳的多目标优化问题。为解决多目标优化问题，Wang等[8]采用加权法将多目标函数转化为单目标问题，但该方法的缺陷在于其加权系数较难确定。马廉洁等[9]结合遗传算法与BP神经网络对微晶玻璃点磨削工艺参数进行了双目标优化，但优化时只考虑了变量的上下限约束条件。

本文在前述研究的基础上，结合碟形砂轮磨齿的特点，综合考虑齿面表面质量、磨削效率等工艺要求和主要约束条件，建立碟形砂轮磨削面齿轮的工艺参数的多目标非线性数学模型，并运用内点罚函数法和遗传算法相结合的策略对此多目标问题进行优化。

1　面齿轮数控磨削工艺参数分析

数控磨削作为面齿轮加工的最终加工工序，其工艺参数的优化重点是：既要保证工件的加工质量，又要考虑数控磨削的加工效率。本文采用数控六轴五联动磨床,加工方式为碟形砂轮磨削面齿轮,其工艺参数包括磨削用量(砂轮磨削速度、进给速度、切深)和碟形砂轮特性参数(主要包括磨料、粒度、硬度、结合剂、组织、浓度、砂轮形状尺寸、硬度等)[10]。磨削用量的选取是否合适将直接影响磨削温度、工件表面粗糙度和加工时间。较大的砂轮磨削速度会使工件表面温度上升、表面粗糙度减小、单位时间内金属去除率提高；进给速度的增大会使表面粗糙度恶化；切深的增大会使工件表面温度升高。砂轮参数的选择应保证磨削表面质量，如粗糙度、金相组织等。砂轮参数中的磨料选择主要根据工件材料类型确定，本文中工件材料为18Cr2Ni4WA，则一般采用具有较好切削性和自锐性的白刚玉较为合适；砂轮粒度的大小选择对加工表面粗糙度有直接影响，根据加工工序的不同和加工精度的要求，精磨时一般选用粒度为60～80#；砂轮硬度是以工件材料的硬度大小为前提进行选择的，工件材料硬度越大，则选取的砂轮硬度越小，但不宜过小，否则将因易脱落而影响砂轮寿命。为减少设计变量、简化数学模型，在此仅考虑将磨削用量作为面齿轮磨削工艺参数的主要优化对象，而将碟形砂轮的相关参数选定为D300×25×127WA80L5R35。

2　工艺参数优化的数学模型

2.1设计变量

根据上述对碟形砂轮数控磨削面齿轮的工艺参数的分析，本文取磨削用量三个参数即砂轮磨削速度vs、进给速度vf、切深ap且分别记为x1、x2、x3作为磨削加工工艺优化问题的设计变量，即

(1)

2.2目标函数

2.2.1磨齿效率

对于面齿轮磨齿加工，在确保齿轮加工质量与避免齿面烧伤的前提下，应尽可能提高加工效率、缩短磨齿时间。而单件齿轮磨削加工时间T包括基本时间T1、辅助时间T2、加工场所准备时间T3、休息时间T4、磨齿加工准备时间T5等。本文建立的磨削加工时间T的数学模型如下：

T = T1+ T2+ T3+ T4+ T5

(2)

对于齿轮参数一定的单件齿轮除了T1，其他时间基本上是不变的，故要提高效率、缩短磨削加工时间只能通过优化T1来实现。建立基本时间T1模型[11]如下:

(3)

式中，d为齿轮分度圆直径，mm ；Z为齿轮齿数；b为磨削齿轮宽度，mm；z为齿轮磨削余量，mm。

2.2.2表面质量

面齿轮磨齿加工后的表面质量直接影响其物理、化学及力学性能，面齿轮的工作性能、可靠性、寿命在很大程度上取决于其表面质量。一般而言，提高产品的表面质量会在很大程度上提高其耐磨性、耐蚀性和抗疲劳破损能力。磨齿的表面质量包括齿面表面粗糙度、表面硬层深度等，常用表面粗糙度Ra对其进行评价。磨削工艺参数与零件的加工表面质量指标及其磨削过程指标间存在一定的幂函数关系，本文采用以砂轮磨削速度、进给速度、切深为变量的表面粗糙度经验公式[12]:

(4)

其中，A为常数项，t、b、c分别为切深、进给速度、砂轮磨削速度的指数，其大小需针对具体加工条件，通过磨削试验数据统计分析，并经多元回归数值分析计算得到，本文中A=2.56，t=0.12,b=0.10,c=-0.48。

2.3约束条件

2.3.1表面粗糙度约束条件

齿轮表面粗糙度对其使用性能和寿命有非常重要的影响。因此磨齿时一个重要的指标就是齿面表面质量，即表面粗糙度不能超过给定的范围Ramax，即

Ra≤Ramax

(5)

首先将A、t、b、c的值代入式(4)，再由所得的式(4)代入式(5)并联立式(1)，整理可得表面粗糙度约束方程G1(x)：

(6)

2.3.2磨削烧伤约束条件

齿轮磨削时为了防止齿面磨削烧伤，需满足以下防止烧伤的条件[13]：

(7)

式中，Cb为由工件材料和砂轮类型决定的磨削烧伤临界系数[13]，Cb= 1920 m·mm/min;ds为砂轮的直径，mm。

将Cb值代入式(7)且联立式(1)可得磨削烧伤约束方程G2(x)：

(8)

式中，x1的单位为m/min;x3的单位为mm。

2.3.3磨削功率约束条件

齿轮磨削时磨削功率需满足一定要求，必须在主轴功率的范围之内:

0.0358(apvfvs)0.7-ηPc≤0

(9)

式中，0.0358(apvfvs)0.7为切削功率[14]；η为机床主电机到主轴间传动效率，取η=0.95[14-15]；Pc为主电机功率。

将η值代入式(9)且联立式(1)可得磨削功率约束方程G3(x)：

2013年，浙江省紧紧围绕新一届省委、省政府提出的“干好一三五、实现四翻番”，建设物质富裕精神富有现代化浙江的工作部署，在水利部的指导和支持下，抓重点、破难点、呈亮点，努力实现开局第一年水利工作“开门红”，确保完成“十二五”水利发展三年主要目标任务，并为今后五年全省水利改革发展开好头、起好步。

G3(x)=0.0358(x1x2x3)0.7-0.95Pc≤0

(10)

2.3.4磨削用量边界约束条件

磨齿时要选取最佳的磨削用量，切深、进给速度、砂轮磨削速度不能超过许可范围，变量边界条件为

vsmin≤vs≤vsmax

(11)

vfmin≤vf≤vfmax

(12)

apmin≤ap≤apmax

(13)

将上述三式联立式(1)整理可得

G4(x)=x1min-x1≤0

(14)

G5(x)=x1-x1max≤0

(15)

G6(x)=x2min-x2≤0

(16)

G7(x)=x2-x2max≤0

(17)

G8(x)=x3min-x3≤0

(18)

G9(x)=x3-x3max≤0

(19)

综上，这是一个含2个目标函数(F1(x)、F2(x)),3个性能约束条件(Gi(x),i=1,2,3),6个边界条件(Gi(x),i=4,5,…,9)的三维非线性优化设计问题,即

(20)

3　优化方法选择

根据前面所建立的工艺参数优化模型和约束条件类型可知，本文所要求解的问题是一个多目标非线性约束的优化问题。通过对上述类型数学模型分析可发现，无法找到一个单一的某一个点让这两个目标同时达到最小。对于该类实际应用问题一般是采取从多目标优化问题的Pareto最优解集合中挑选一个或一些解作为所求多目标优化问题的最优解[16]。目前存在多种求解多目标优化问题的方法，如线性加权法、理想点法等；针对约束优化问题的处理办法现主要有丢弃法、修理法、修改遗传算子法和惩罚函数法。这些求解方法各有优势与弊端。本文采用内点罚函数法与遗传算法相结合的策略进行求解。多目标优化问题描述如下：

(21)

式中，X为待优化的变量；fi(x)为待优化的目标函数；r为变量个数；s为目标函数个数；g(x)为约束条件函数；p为约束条件个数。

3.1内点罚函数法(内点法)

式中，minf(x)为求最小目标函数；Gj(x)为不等式约束函数条件。

构造惩罚函数为

本文参照内点法构造惩罚函数原理，将面齿轮磨削工艺参数优化的数学模型(式(20))中3个性能约束条件(Gi(x),i=1，2，3)作为罚项加入目标函数(f1(x)、f2(x))构成罚函数，即

(22)

则面齿轮磨削工艺参数优化的多目标约束数学模型(式(20))就转化为

(23)

可以看出，式(23)是一个仅含变量上下限约束条件的多目标优化问题。

3.2基于遗传算法的多目标优化算法

函数gamultiobj[17]受控的精英遗传算法是NSGA-Ⅱ算法的改进型，它包含在MATLAB遗传算法与直接搜索工具箱(GADST)中。该函数适用于求解只含变量上下限约束条件和线性约束条件的多目标问题。面齿轮磨削工艺参数优化的多目标数学模型即式(20)经内点法处理后，已转化为式(23)，式(23)只含变量上下限约束条件无非线性约束条件，显然符合函数gamultiobj适用范围,则本文利用函数gamultiobj对式(23)进行求解。本文采取通过GUI界面调用的方式，即：首先，将式(23)中罚函数(M1(x)、M2(x))编辑成m文件作为适应度函数，并命名保存在函数gamultiobj界面工作目录下以便调用;其次，打开函数gamultiobj界面并输入其所需相关参数(种群大小、迭代次数等)；最后，运行该界面即可。

综上所述，面齿轮磨削工艺参数优化的多目标优化问题求解的基本流程如下所示：

(1)确定惩罚因子μ的值。根据内点法惩罚因子选取的原则，需经多次试验调整和运行程序以确定合适的值。

(2)编写面齿轮磨削工艺参数优化的适应度函数m文件。首先将式(3)、式(4)、式(6)、式(8)、式(10)代入式(22)中形成罚函数；再通过MATLAB程序编辑器将罚函数形成m文件作为本次研究中的适应度函数。

(3)通过GUI界面调用函数gamultiobj并确定有关设置参数。需设置的有关参数主要有：种群大小、进化代数与停止代数、交叉概率、变异概率、最前端系数、适应度函数值偏差。

(4)在函数gamultiobj界面输入适应度函数、变量个数值、变量上下界以及线性约束条件。本文所研究的变量个数为3，即x1、x2、x3；变量上下界分别为变量边界条，即式(14)～式(19)中各个变量(x1、x2、x3)的最大值和最小值；线性约束条件本文中为空。

(5)开始求解。

4　优化仿真及实验

仿真中面齿轮参数及加工参数如表1所示。

表1　面齿轮参数及加工参数

4.1优化仿真

本文以MATLAB7.6为平台，先将上述面齿轮加工参数代入适应度函数，再运用遗传算法与直接搜索工具箱(GADST)。经多次运行MATLAB程序和试算后，确定合适的有关参数如下：惩罚因子μ=0.0001、设置的种群大小为80、进化代数与停止代数也均为80、交叉概率为0.8、变异概率为0.01、最前端系数为0.2、适应度函数值偏差为1×10-10，其余设置为默认。

通过程序运行结束后，将Workspace中得到的Pareto解集及x对应的适应度函数值列于表2。同时根据表2中磨削时间T1和表面粗糙度Ra的值利用MATLAB程序绘制适应度函数Pareto解第一前端个体分布图，见图1。

表2　某次运行得到的Pareto解

由图1可以清晰地了解到两个适应度函数的Pareto解分布情况，同时也可看出无法找到某一个点使两个优化目标函数值同时最小。而表2中优化结果则表明：采用内点法与基于遗传算法的多目标优化算法相结合的优化策略对面齿轮磨削工艺参数进行多目标优化时，可以找到多组工艺参数对磨削面齿轮进行加工指导；多组操作参数在协调多个生产目标上各有优劣。因此，生产者可以从多组的优化参数中找到一组或几组操作参数来对当前的生产状况进行相应调整，这体现了该方法的优势。

图1　适应度函数Pareto解第一前端个体分布图

根据面齿轮磨削加工的实际情况可知：表2中第1组～第5组数据显示磨削基本时间T1较短，但其值与生产实际不符且表面粗糙度值较大；第9组～第16组数据显示表面粗糙度值Ra较小，但生产效率较低。故当表面质量要求较高时可选表2中第8组中的磨削用量；当要求生产效率要求较高时可选第6组中的磨削用量；当生产效率与表面质量同时要求较高时可选择第7组中的磨削用量。此三组相对应的性能约束函数值(表3)均为负值且各设计变量优化值均在相对应的边界范围内，故满足前述约束条件。

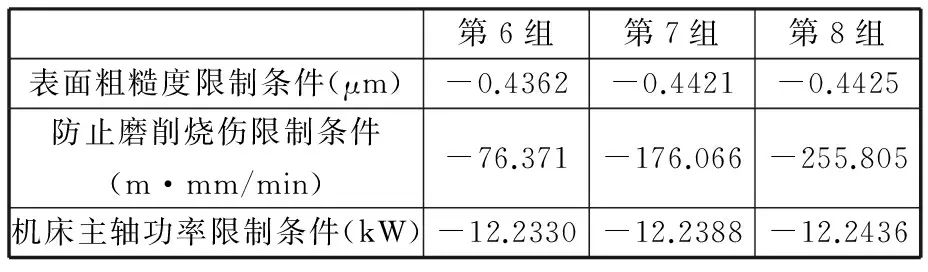
表3　最优点的非线性约束函数值

4.2实验

为了验证优化方法及结果的有效性，依据工艺参数优化实验的方法设计并进行实验。本次实验在叶片磨床QMK50A进行，磨轮为碟形砂轮(D300×25×127WA80L5R35)，磨削液用水基成磨削液，齿轮热处理为HRC56～63；其他面齿轮有关加工参数与仿真相对应相同。对选用的磨削用量每组做三次实验，并采用德国生产的表面轮廓仪Hommel Werke T800(精度可达0.001 μm)测量表面粗糙度，取样长度为0.8 mm，评定长度为取样长度的6倍，面齿轮磨削面Ra测量三次，取其平均值作为实验的表面粗糙度实测值。实验后测量结果如表4所示。

表4列出了三组磨削面齿轮优化前的有关数据，其中数据1是要求高生产效率时所选的磨削用量；数据2是要求高表面质量时所选的磨削用量；数据3是同时要求生产效率和表面质量时所选的磨削用量。通过对比优化前后的相关结果，可以看出优化后的工件表面质量与加工时间都有一定的改善。另外，优化后的磨削基本时间相对误差的最大绝对值为5%，表面粗糙度相对误差的最大绝对值为10.4%，在误差允许范围内。

表4　面齿轮磨削工艺参数优化实验结果

5　结论

(1)针对面齿轮磨削加工，建立了以磨削基本时间和表面粗糙度为加工目标函数的优化数学模型，通过该模型确定了加工目标与磨削用量参数(砂轮磨削速度、进给速度、切深)之间的非线性函数关系。

(2)提出了将内点罚函数法与遗传算法相结合的方法，利用内点罚函数算法将有约束的优化问题转化为无约束问题和函数gamultiobj求解多目标优化问题,对面齿轮磨削工艺参数的多目标优化模型进行求解。

(3)通过优化结果及实验可知：在使用直径为300 mm白刚玉碟形砂轮磨削面齿轮加工过程中，当选用砂轮磨削速度34.354 m/s、进给速度4.927 m/min及切深0.032 mm时，磨削加工基本时间最大优化率为26.2%，当选用砂轮磨削速度34.403 m/s、进给速度5.345 m/min及切深0.026 mm时，齿面表面粗糙度最大优化率为34.3%；要获得要求较高的表面质量与加工效率时，应尽量选较大的砂轮磨削速度、较小的进给速度和切深。

[1]Stadtfeld H J. Coniface Face Gear Cutting and Grinding[CB/OL].Kassel:Gleason Corp Oration,[2011-07-15].http://www.gearsolutions.com/article/detail/6020/confiface-face-Gear-cutting-and-grinding.

[2]Guingand M, Vaujany J P, Jacquin C Y. Quasi-static Analysis of a Face Gear under Torque[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 94:4301-4318.

[3]刘伟，邓朝晖，万林林，等.基于正交试验-遗传神经网络的陶瓷球面精密磨削参数优化[J]. 中国机械工程,2014,25(4):451-455.

Liu Wei， Deng Zhaohui，Wan Linlin, et al. Optimization on Precision Grinding of Ceramic Sphere Using Orthogonal Experiment and Genetic Neual Netword[J]. China Mechanical Engineering,2014,25(4):451-455.

[4]Venkata R R, Pawar P J. Parameter Optimization of Multi-pass Milling Process Using Non-traditional Optimization Algorithms[J].Applied Soft Computing,2010,10(2):445-446.

[5]Yildiz A R. Hybrid Taguchi-differential Evolution Algorithm for Optimization of Multi-pass Turning Operations,2013,13(3):1433-1439.

[6]Savadamuthu L，Muthu S，Vivekanandan P. Optimization of Cutting Parameters for Turning Process Using Genetic Algorithm[J].European Journal of Scientific Research,2012,69(1):73-80.

[7]Ho W H, Tsai J T, Lin B T, et al. Adaptive Network Based Fuzzy Inference System for Prediction of Surface Roughness in End Milling Process Using Hybrid Tagnchi-genetic Learning Algorithm[J]. Export Systems with Applications, 2009,36:3216-3222.

[8]Wang Yaping, Pham H. A Multi-objective Optimization of Imperfect Preventive Maintenance Policy for Dependent Competing Risk Systems with Hidden Failure[J].IEEE Transactions on Reliability,2011,60(4):770-781.

[9]马廉洁,曹小兵,巩亚东,等.基于遗传算法与BP神经网络的微晶玻璃点磨削工艺参数优化[J].中国机械工程,2015,26(1):102-106.

Ma Lianjie,Cao Xiaobing,Gong Yadong, et al. Process Parameter Optimization Based on BP Neural Networks and GA in Point Grinding Low Expansion Glass[J]. China Mechanical Engineer-ing,2015,26(1):102-106.

[10]Litvin F L,Fuentes A,Handschuh R F,et al.Face-gear Drives with Spur Involute Pinion:Geomtery Generation by a Worm, Stress Analysis[J].Computer Methods in Appl. Mech. and Eng., 2002, 191:2785-2813.

[11]赵大兴,张颂,丁国龙,等.成形磨齿工艺参数多目标优化研究[J].组合机床与自动化加工技术,2014(2):117-120.

Zhao Daxing, Zhang Song, Ding Guolong, et al.Multi-object Optimization of the Technology Parameters of Gear Form Grinding[J].Modular Machine Tool & Automatic Manufacturing Techniq-ue,2014(2):117-120.

[12]亓剑.磨削表面粗糙度预测及实验研究[D].天津:天津职业技术师范大学,2015.

[13]任敬心,华定安. 磨削原理[M].北京:电子工业出版社,2011.

[14]王晋，赵鹏兵.无心磨削工艺参数的非线性优化研究[J].机床与液压,2011, 39(21):81-83.

Wang Jin, Zhao Pengbing. Research of Nonlinear Optimization on Process Parameters of Centerless Grinding[J].Machine Tool&Hydraulics,2011,39(21):81-83.

[15]丁军鹏.齿轮成形磨削工艺参数优化及实验研究[D].洛阳:河南科技大学,2011.

[16]田槐艳.非石棉垫片配方的分类及优化仿真[D].昆明：昆明理工大学,2010.

[17]Kalyanmoy D,Amrit P,Sameer A,et al.A Fast and Elitist Multiobjetive Genetic Algoithm:NSGA -Ⅱ[J].IEEE Transaction on Evolutionary Comuta-tion,2002,6(2):182-197.

(编辑袁兴玲)

Grinding Parameter Optimization of Face Gears

Ming Xingzu1Luo Dan1Liu Jinhua1Yan Hongzhi2

1.Hunan University of Technology，Zhuzhou，Hunan，412007 2. Central South University, Changsha，410083

Based on the analyses of the grinding parameters of face gears, under the conditions of meeting product quality requirements and other design constrains, a multi-objective optimization mathematical model was established, which took grinding efficiency and surface quality as the objective function. The interior penalty function method and genetic algorithm were used to solve the multi-objective optimization model,and three groups of the best scheme of grinding conditions were obtained, that might make the grinding efficiency and surface quality be improved. Experiments were performed according to optimized results. The effectiveness and practicability of this method were validated by analyses and applications.

face gear; grinding; processing parameter; multi-objective optimization; interior penalty function method; genetic algorithm

2015-11-30

国家自然科学基金资助项目(51375161,51575533)；湖南省自然科学基金资助项目(2015JJ5018)

TH132.41

10.3969/j.issn.1004-132X.2016.19.003

明兴祖，男，1964年生。湖南工业大学机械工程学院教授、博士。研究方向为数字化制造理论与技术。发表论文40篇。罗旦(通信作者)，男，1991年生。湖南工业大学机械工程学院硕士研究生。刘金华，女，1964年生。湖南工业大学机械工程学院教授。严宏志，男，1964年生。中南大学机电工程学院教授、博士研究生导师。