正弦变载荷工况下液压泵振动信号的形态学滤波方法

刘思远　杨梦雪　王　闯　张文文

1.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，066004 2.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004



正弦变载荷工况下液压泵振动信号的形态学滤波方法

刘思远1,2杨梦雪1,2王闯1,2张文文2

1.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，066004 2.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004

液压泵的振动信号在受到大幅度变载荷作用时将引起振动特征的变化，特别是在正弦载荷变化的作用下，将会产生幅值调制现象。采用传统的单一尺度结构元素的形态学方法对该类信号进行滤波的效果不一定理想。因此，针对正弦载荷液压泵振动信号的特点，在单尺度形态滤波分析方法的基础上，提出了兼顾形态学结构元素长度和高度尺度的多尺度形态学滤波方法。首先，以冲击特征比值和二阶原点矩作为评价指标，提出综合考虑结构元素长度和高度尺度的寻优方法，确定最优长度和高度尺度算子组合。然后，用最优尺度组合对正弦载荷模拟仿真信号和变载荷液压泵故障振动信号进行滤波处理，分析结果证实其滤波效果优于单尺度滤波方法滤波效果。

变载荷；液压泵；形态滤波；多尺度

0　引言

现实生活中绝对的稳态条件是不存在的。实际上，机械的非稳态信号包含着比稳态振动信号更丰富的信息，可以反映更多的系统特性。在稳态情况下本来不容易显现出来的现象在非稳态工况条件下可以得到充分的显现[1]。

非稳态振动信号表现出的振动特征与稳态信号是有差别的，需要在传统滤波方法的基础上研究新的滤波方法来解决振动信号的非稳态问题。目前，在液压系统振动信号的滤波方法研究方面，很多都以液压泵为研究对象。文献[2]用小波包变换对振动信号进行了有效处理，从而实现对液压泵的故障检测。文献[3]利用粒子数优化后的粒子滤波算法对飞机液压泵振动信号进行了有效降噪。文献[4]采用小波包分析技术解决了泵出口故障检测信号信噪比低、难以进行故障特征提取的问题。文献[5] 通过对传统小波分析方法得到的信号进行渐近式权值的选择，得到了信噪比较好的降噪信号，并从中选取了最优特征集。以上方法在定工况的条件下都取得了较好的滤波效果，但在变工况条件下是否适用并没有研究。

液压泵在实际工作中，往往由于工况的复杂性，使自身处于变工况条件下。当液压泵出现故障时，所测到的信号往往具有非线性非平稳性特征。如何准确、快速地提取信号中的特征信息成为液压系统故障诊断领域的难点和热点问题。对此，Serra[6-7]提出了基于积分几何和随机集理论的数学形态学，然后将其引入到信号处理的领域中。形态滤波理论具有非常有效的非线性、非平稳滤波技术[8]，在故障诊断领域具有良好的应用前景。文献[9]提出了一种通过确定最优扁平型结构元素长度以实现最优滤波的形态滤波方法，并在液压泵故障信号的滤波过程中取得了较好的应用效果；文献[10]针对液压泵故障信号提出了一种基于最优结构元素长度的形态滤波方法，并在此基础上对基于限定阈值的自适应多尺度形态滤波方法进行了研究，其滤波效果都得到了较好的印证。以上方法的研究是在不考虑载荷振动信号幅值调制问题的条件下取得的。这些方法在处理变载荷振动信号时不一定能取得较好的滤波效果。

为此，本文在以上研究的基础上避免了单尺度形态学分析在结构元素选择时的盲目性和对相关先验知识的依赖性，提出了以冲击特征比值和二阶原点矩作为复合评价指标，综合考虑结构元素长度尺度和高度尺度的多尺度寻优形态滤波方法。通过仿真分析给出该方法的具体实现步骤；通过正弦变载荷工况的液压泵故障模拟及信号分析试验对该方法进行验证。

1　多尺度形态学理论基础

1.1多尺度形态运算[11]

多尺度形态学最初是基于形态学结构元素的分解提出的，目的是提高大尺度结构元素形态学运算速度和扩展形态学图像处理方法的应用范围。多尺度形态学可以定义为采用不同尺度的结构元素对信号进行形态学变换。

假设T为形态学变换，X为信号，则基于T的多尺度形态学变换可定义为一簇形态学变换{Ts|s>0,s∈Z},其中Ts定义为

Ts(X)=sT(X|s)s>0

(1)

设f(n)和g(m)分别为定义在F={0，1，…，N-1}和G={0，1，…，M-1}上的离散函数，f(n)为输入信号，g(m)为结构元素，则多尺度形态膨胀和腐蚀可分别定义为

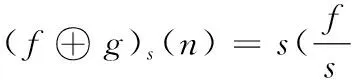
(2)

(3)

n=0,1,…,N-1

其中，sg为尺度s下的结构元素，且sg为g经过s-1次自身的膨胀所得：

sg=g⊕g⊕…g

(4)

由此可以推出，对于由腐蚀和膨胀运算通过级联、并或交所构成的一般形态学运算T，基于T的多尺度运算就是将T中所有腐蚀、膨胀变换所使用的g进行s- 1次膨胀运算。对于一维信号，结构元素的尺度信息包括长度和高度两个因素，则多尺度形态学分析中的尺度s分解为长度尺度sl和高度尺度sh，即s= {sl，sh}。也就是说，一维信号的多尺度形态学分析所采用的结构元素由sl和sh共同确定。

1.2差值滤波器

以4种基本形态算子T为基础，根据液压泵故障呈现的冲击特征，构建差值滤波器模型。差值滤波器模型结构为

f·g-fog=(f·g-f)+(f-fog)

(5)其中，f·g-f被称为形态学的黑Top-Hat变换，用于提取信号中的负冲击；f-fog被称为形态学的白Top-Hat变换，用于提取信号中的正冲击。

1.3冲击特征比值

形态滤波器的参数设置会严重影响信号滤波的效果。为此定义冲击特征比值来定量分析形态滤波频域特征的提取效果：

(6)

其中，fi为特征频率的i倍频对应的功率谱密度峰值；M′为最高倍频数，取M′=3；N′为总谱线数。K为频域中信号特征频率与其余频率的比值，K值的大小反映了信号特征频率在频谱图中的突出程度。K值越大，则特征频率越突出，特征提取的效果越好；K值越小，特征频率越不明显。

2　正弦变载信号模拟及滤波仿真分析

采用含噪仿真信号来模拟受正弦载荷干扰且幅值连续变化的液压泵振动信号。含噪仿真信号表达式为

x(t)=x1(t)+x2(t)x3(t)+x4(t)

(7)

式中，x1(t)为频率为16 Hz的周期性指数衰减信号，每周期内冲击函数为8e-500tsin(512πt)，用于模拟故障信号；x2(t)为20 Hz低频信号，其表达式为x2(t)=sin(40πt)；x3(t)为频率为0.05 Hz的正弦波信号，其表达式为x3(t)=cos(0.1πt)；x4(t)是标准差为1的高斯白噪声，用于模拟强背景噪声。

式(7)中，x2(t)x3(t)用于模拟正弦载荷工况下液压泵振动信号，图1a为故障信号时域图，图1b为变载荷振动信号的时域波形。

设定采样频率为2048 Hz，截取采样时长为1 s。图1c所示是混合信号在1s内的时域波形，从中很难分辨脉冲成分。从图1d中可以看出，冲击信号被谐波信号和高斯白噪声信号完全淹没，无法通过原始信号功率谱图找到冲击特征频率成分。

图1　故障信号仿真

2.1形态滤波的影响因素

形态滤波的效果不仅取决于所采用的形态运算算子，而且还与所采用的结构元素密切相关。结构元素主要包括结构元素的类型、长度(定义域)、高度(幅值)。考虑这些因素的影响，选择正确的形态算子和结构元素是解决变载荷振动信号滤波问题的关键。

2.1.1结构元素形状对形态滤波的影响

根据所处理信号的形状特征，可以选择直线、正三角形、正方形、正弦等各种不同的结构元素。

为比较各种结构元素形状的差异性，选择常用的三种形状，选取长度尺度为2～80计算冲击特征比值，如图2所示。从图中可以看出，三角形的结构元素对冲击特征的提取效果最佳，半圆形次之，扁平形最差。

图2　不同结构元素形状的冲击特征比值

2.1.2算子对形态滤波的影响

不同的形态算子对信号具有不同的滤波效果，通常根据信号处理的目的选择形态算子。对式(7)仿真信号进行滤波处理的目的就是消除或减小白噪声及谐波信号的干扰，突出脉冲信号的特征频率。而开运算可以抑制正冲击、保留负冲击，差值运算可以同时提取信号中的正冲击和负冲击，因而可以选用开运算或差值运算进行信号处理。采用三角形结构元素(高度尺度为1)对仿真信号分别进行形态开运算和差值运算，求取其冲击特征比值，结果如图3所示。由图3可知，差值运算能够更好地提取信号的故障冲击特征，这与差值算子可以同时提取出信号中的正负脉冲的结论是一致的。

图3　不同形态算子的冲击特征比值

2.1.3结构元素长度尺度对形态滤波的影响

设计差值滤波器，选取结构元素形状为三角形，设定高度尺度为1，分别取长度为 5、13、28，对式 (7) 所示仿真信号进行形态滤波，结果如图4所示。

从图4中可以看出，随着长度尺度的增加，故障特征频率16Hz及其倍频处的谱峰更为清晰，信号中噪声成分的谱峰明显减小。由此说明增加长度尺度能有效地提取特征频率，且长度尺度越大，特征频率的谱峰越明显。但是，随着sl的增加，16Hz的6倍频处的特征频率越来越不明显，且在信号的16Hz基频到零频段出现了一些峰值较大的干扰频率。由此可以看出，盲目增大长度尺度显然无法获得好的滤波效果。

2.1.4结构元素高度尺度对形态滤波的影响

设计差值滤波器，选取结构元素形状为三角形，长度尺度设定为13，分别取高度为 2、8、20，对式 (7) 所示仿真信号进行形态滤波，结果分别如图5所示。

(a) sl=5

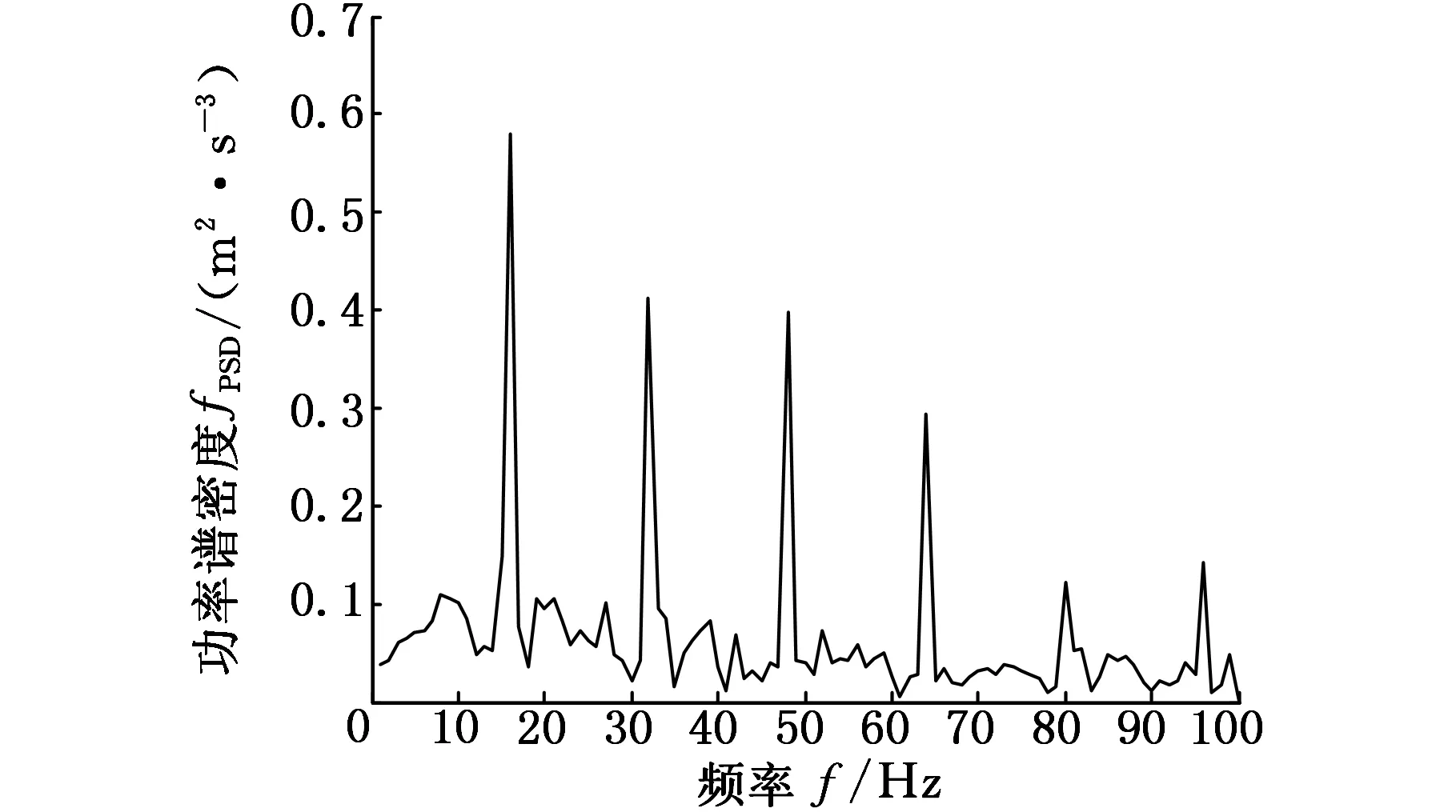
(b) sl=13

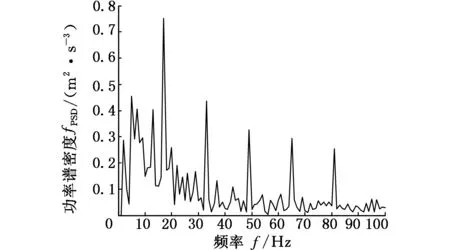
(c) sl=28图4　长度尺度不同时形态滤波信号的功率谱

从图5中可以看出，随着高度尺度的增加，16Hz及其倍频处的特征频率对应峰值有明显的增长。这说明，高度尺度在一定范围内的增加可以有效提高该类仿真信号的形态滤波效果，且不会出现倍频减少的现象。

2.1.5多尺度寻优

当高度尺度确定，结构元素长度较小时，信号噪声成分不能被很好地滤除，故障特征频率处的峰值较小，特征频率谱峰不明显；随着结构元素长度的增加，信号中的噪声成分明显减少，故障冲击特征频率及其倍频处的谱峰更为清晰；当结构元素长度继续增长超过阈值时，故障冲击特征频率的一倍频非常突出，但在信号故障特征频率到零频段会出现幅值较大的干扰频率谱峰，并且丢失了信号中更多的细节信息，特征频率的倍频成分越来越不明显。针对以上结论，将信号故障特征频率基频到零频段频率幅值的二阶原点矩作为一个评价指标，与冲击特征比值共同组成复合评价指标，同时指导寻找结构元素最佳长度尺度。

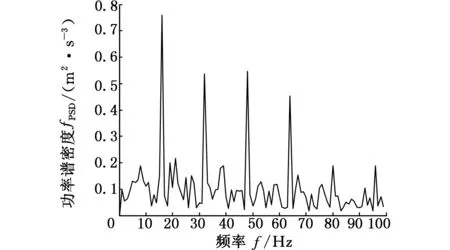
(a) sh=2

(b) sh=8

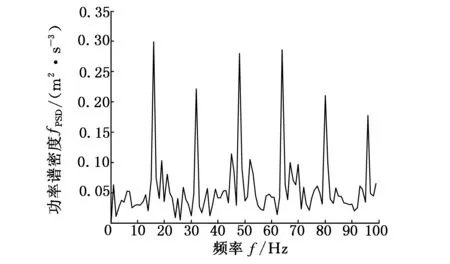
(c) sh=20图5　高度尺度不同时形态滤波信号的功率谱

任意取4组高度尺度的值sh=35、40、45、50，分别分析其冲击特征比值随长度尺度的变化规律，如图6所示。每一条曲线都能找到一个最大冲击特征比值对应的长度尺度，并且在该长度尺度下计算出的故障特征频率基频到零频段的二阶原点矩较小，均未出现干扰频率的影响。因此，可以认为此时结构元素长度为对应此高度尺度的最优长度。仿真过程取了80个高度尺度(1～80)的值均获得了以上规律。利用上述同样的方法作出80条曲线，每条曲线都能找到一个对应的最优长度尺度。将80条曲线的最大冲击特征比值作为纵坐标，对应的高度尺度作为横坐标，得到如图7所示的曲线。

图6　多尺度寻优图

综上，找到对应最大冲击比值的长度尺度和高度尺度的最优组合为s={11，47}，且此时曲线较为稳定，滤波效果将会较好。

2.2多尺度形态滤波效果分析

利用多尺度和单尺度方法对仿真信号分别进行滤波分析，如图8所示。对比两个功率谱图可以发现,综合考虑长度和高度结构元素多尺度寻优后的仿真信号功率谱在16Hz及其倍频位置特征频率对应的峰值很明显，而文献[10]的单尺度滤波方法仅对长度进行寻优后的功率谱在16Hz及其倍频处的峰值并不十分突出，而且在5倍频和6倍频位置处的特征频率无法分辨，峰值基本消失。

(a)多尺度形态滤波

(b)单尺度形态滤波图8　两种方法的功率谱分析

通过信噪比的计算得出多尺度形态滤波信号的信噪比为11.6，高于单尺度形态滤波信号的信噪比9.0。

通过以上分析得知，针对变载荷振动信号的幅值调制问题，多尺度形态滤波方法对正弦变载荷模拟信号的滤波效果要优于单尺度形态滤波。

3　多尺度形态学滤波方法

本文利用仿真分析的结论在文献[10]的方法基础上进行改进，同时兼顾长度和高度两种尺度对正弦变载荷工况条件下泵的振动信号进行多尺度形态滤波。具体方法实现的步骤如下：

(1)采集泵端盖振动信号，建立一维离散时间向量；

(2)确定最优结构元素形状，建立差值滤波器模型；

(3)利用冲击特征比值和二阶原点矩两个特征指标构建形态滤波的复合评价体系；

(4)依据复合评价体系尺度寻优原则，选择长度和高度尺度组合(sl,sh)；

(5)利用确定好的s=(sl,sh)对步骤(1)构建的一维离散时间向量进行多尺度形态滤波处理。

尺度寻优原则：

(1)确定择优区间，首先确定长度尺度的择优区间，再根据长度小(大)尺度对应高度小(大)尺度[12]的方法确定高度尺度的择优区间；

(2)作出高度尺度区间范围内每个高度尺度值对应的冲击特征比值K随长度尺度变化的曲线，找到每条曲线中最大K值对应的长度尺度，且要保证此时的二阶原点矩数值较小；

(3)对每条曲线的最大K值进行比较，找出其中最大的一个，它所对应的 (sl,sh)即为所求最优组合。

4　液压泵故障模拟试验分析

本试验是在材料试验机液压伺服系统试验平台上完成的，试验台如图9所示。以MCY14-1B型号轴向柱塞泵为研究对象，电机额定转速设为1500r/min。设置采样频率为50kHz，并对泵端盖的振动信号进行数据采集。人为设计轴向柱塞泵分别在正常状态、单柱塞滑靴磨损和中心弹簧失效三种工作状态下进行试验研究。试验初始压力调定为5MPa，截取1s时间段的数据进行分析。在这段时间里设置一正弦加载信号作用于液压泵出口(模拟正弦载荷变化)。

图9　液压泵故障模拟试验台

液压泵各类工作状态的原始信号时域波形如图10所示。从图10可以看出，在0≤t<1s时间段内液压泵振动信号的幅值有明显的变化。但是从时域波形中无法发现表征液压泵各工作状态的显著特征信息。对原始信号进行功率谱分析，如图11所示。从功率谱图中发现各工作状态的特征频率完全被噪声信号所淹没，无法找到反映液压泵各种工作状态的特征频率。

图10　原始信号时域波形

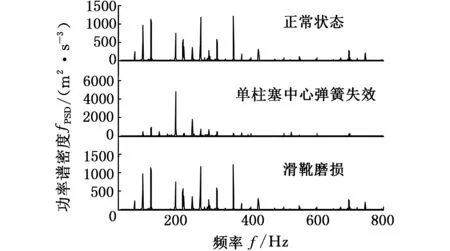
图11　原始信号频域波形

根据多尺度形态学分析方法的多尺度寻优原则和单尺度形态学分析方法中最优结构元素长度的选择原则，计算得到正常状态、中心弹簧失效和单柱塞滑靴磨损三种工作状态的各尺度值，如表1所示。

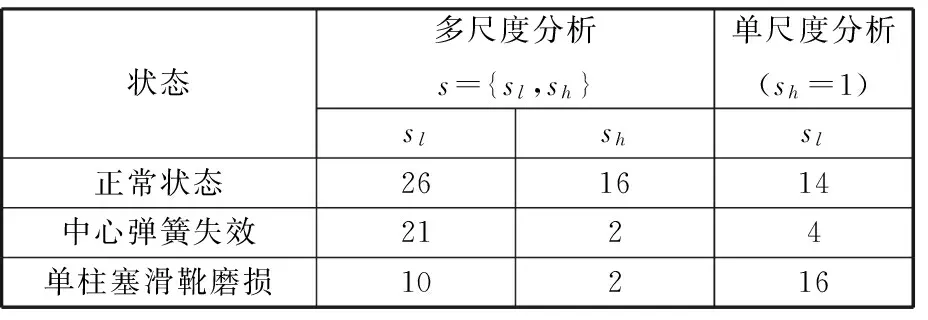
表1　最优尺度选择

利用形态学分析方法进行滤波得到滤波信号。对滤波信号进行功率谱分析 (图 12 、图 13 )，可以得出以下结论：

(1)比较图12a和图13a可以看出，虽然单尺度滤波方法得到的滑靴冲击斜盘的特征频率175 Hz能量幅值更大，但是却找不到350 Hz的流量脉动频率。而多尺度形态滤波方法，既能找到175 Hz特征频率，也能找到350 Hz流量脉动频率，且能量幅值显著。

图12　单尺度滤波信号功率谱图

图13　多尺度滤波信号功率谱图

(2)比较图12b和图13b可以看出，当发生中心弹簧故障时，单尺度滤波方法得到的功率谱除能够明确地找到特征频率175 Hz 和 350 Hz外，还在转轴频率的6倍频处(150 Hz)和15倍频(375 Hz)处出现很明显的能量峰值；而多尺度滤波方法得到的功率谱除 175 Hz，在 25 Hz 转轴频率基频、4倍频(100 Hz)、6倍频(150 Hz)以及13倍频(325 Hz)位置却出现了明显的能量峰值，多尺度滤波方法能发现更多的信号特征信息。依据中心弹簧失效故障机理可知，25 Hz 基频及其倍频均是该故障的特征频率。

(3)比较图12c和图13c可以看出，当单柱塞滑靴磨损故障发生时，单尺度滤波方法得到的功率谱特征频率除175 Hz和350 Hz的能量幅值有所增加外，没有其他特征频率发生变化；而多尺度滤波方法得到的功率谱不仅在175 Hz和350 Hz的能量幅值有明显的增加，而且在25 Hz基频、2倍频(50 Hz)、4倍频(100 Hz)以及13倍频(325 Hz)等处出现了明显的能量峰值。根据单柱塞滑靴磨损的故障机理可知，25 Hz基频恰恰是该故障的特征频率，与此同时，通过该滤波方法还找到了反映该故障的另外几个特征频率。

通过信噪比的计算得出，正常状态工况条件下多尺度形态滤波信号的信噪比为4.2，高于单尺度形态滤波信号的信噪比2.2；中心弹簧失效工况条件下多尺度形态滤波信号的信噪比为3.7，高于单尺度形态滤波信号的信噪比3.5；单柱塞滑靴磨损工况条件下多尺度形态滤波信号的信噪比为3.5，高于单尺度形态滤波信号的信噪比2.9。

综上所述，单尺度形态滤波方法对正弦变载荷工况下泵不同状态时振动信号表现出的频率特征反映并不明显。而多尺度形态滤波方法则能明显地反映出泵各种状态下的频率特征。由此证明，多尺度形态滤波方法比单尺度滤波方法更适用于正弦变载荷振动信号，且能获得更佳的滤波效果。

5　结论

(1)给出了具体的结构元素和运算算子的选择方法，解决了原有单尺度形态学分析时结构元素选择的盲目性和对相关先验知识的依赖性问题。仿真分析证明该方法可以有效地提取信号冲击成分而较好地抑制噪声的影响。

(2)多尺度形态滤波能够对液压泵不同状态的正弦变载荷振动信号进行多尺度寻优，并能有效解决其振动信号的幅值调制的问题。

(3)通过试验验证，综合考虑长度尺度和高度尺度的多尺度形态滤波方法能够对液压泵正弦变载荷工况下的振动信号进行有效滤波，与单尺度形态滤波方法相比，滤波效果更好。

[1]朱继梅.非稳态振动信号分析(连载) [J].振动与冲击,2000, 19(2): 87-90.

Zhu Jimei. Unsteady Vibration Signal Analysis (serial) [J]. Journal of Vibration and Shock, 2000, 19 (2):87-90.

[2]Muralidharan V, Sugumaran V, Sakthivel N R. Wavelet Decomposition and Support Vector Machine for Fault Diagnosis of Monoblock Centrifugal Pump[J]. Int. J. Data Anal. Tech. Strat.，2011,3(2):159-177.

[3]刘玉娇,姚恩涛,徐红专.基于粒子滤波和自回归谱的液压泵故障诊断[J].仪器仪表学报,2012,33(3):561-567.

Liu Yujiao, Yao Entao, Xu Hongzhuan. Fault Diagnosis of Hydraulic Pump Based on Particle Filtering and Autoregressive Spectrum [J]. Chinese Journal of Scientific Instrument, 2012, 33(3)：561-567.

[4]王少萍,苑中魁,杨光琴.基于小波消噪的液压泵故障诊断[J].中国机械工程,2004,15(13)：1161-1163.

Wang Shaoping, Yuan Zhongkui, Yang Guangqin. Sudy on Fault Diagnosis Based on Wavelet for Hydraulic Pump [J]. China Mechanical Engineering, 2004, 15(13)：1161-1163.

[5]李胜,张培林,吴定海,等.基于渐近式权值小波降噪和Adaboost算法的液压泵故障诊断[J].中国机械工程,2011,22(9):1067-1075.

Li Sheng, Zhang Peilin, Wu Dinghai, et al. Hydraulic Pump Fault Diagnosis Based on Gradual Weight Wavelet Noise Reduction and Adaboost Algorithm [J]. China Mechanical Engineering, 2011, 22(9):1067-1075.

[6]Serra J. Image Analysis and Mathematical Morphology, Theoretical Advances, Vol. 1[M]. New York： Academic Press, 1982.

[7]Serra J. Image Analysis and Mathematical Morphology, Theoretical Advances, Vol. 2[M]. New York：Academic Press,1988.

[8]沈路,周晓军,张文斌,等.广义数学形态滤波器的旋转机械振动信号降噪[J].振动与冲击,2009,28(9):70-73．

Shen Lu, Zhou Xiaojun, Zhang Wenbin, et al. Rotating Machinery Vibration Signal Noise Reduction of Generalized Mathematical Morphological Filter [J]. Journal of Vibration and Shock, 2009,28(9):70-73.

[9]姜万录,郑直,朱勇, 等.基于最优扁平型结构元素长度的液压泵故障诊断研究[J].振动与冲击, 2014,33(15)：35-41.

Jiang Wanlu,Zheng Zhi, Zhu Yong, et al. Hydraulic Pump Fault Diagnosis Based on Optimal Flat Structure Element Length [J]. Journal of Vibration and Shock, 2014, 33(15)：35-41.

[10]李扬.形态学滤波新方法及其在旋转机械故障诊断中的应用[D].秦皇岛：燕山大学, 2013.

[11]李兵,张培林,米双山,等.机械故障信号的数学形态学分析与智能分类[M].北京:国防工业出版社,2011.

[12]章立军.信号的数学形态学分析方法及其应用的研究[D].北京：北京科技大学,2007.

(编辑袁兴玲)

Morphological Filtering Method for Vibration Signals of Hydraulic Pump under Sinusoidal Variable Load Conditions

Liu Siyuan1,2Yang Mengxue1,2Wang Chuang1,2Zhang Wenwen2

1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University, Qinhuangdao, Hebei, 066004 2. Key Laboratory of Advanced Forging & Stamping Technology and Science (Yanshan University),Ministry of Education of China, Qinhuangdao, Hebei, 066004

Vibration characteristics of the pump vibration signals would change when they suffered a significant variable loads, especially in the role of sinusoidal load changes, and would produce amplitude modulation phenomenon. The filtering effects of the traditional single-scale structure element morphological methods was not necessarily ideal to this kind of signals. Therefore, for vibration signal characteristics of sinusoidal load pump, on the basis of the single-scale morphological analysis, a multi-scale morphological filtering method was proposed, which took both of length and height scale of the morphological structure elements. Firstly, taking the impact feature ratio and second geometric moment as characteristic index, then, the optimization method of structural elements length scale and height scale was proposed, which determined the optimal length and height scale operator combination. Afterwards, filtering the sinusoidal load simulation signals and variable load hydraulic pump failure vibration signals using the optimal scale combination, the results confirm that the filtering effectiveness is better than that of single-scale filtering method.

variable load; hydraulic pump; morphological filtering; multiscale

2015-12-28

国家自然科学基金资助项目(51505411)；国家重点基础研究发展计划(973计划)资助项目(2014CB046405)

TP277

10.3969/j.issn.1004-132X.2016.19.001

刘思远，男，1981年生。燕山大学机械工程学院副教授。主要研究方向为旋转机械故障的智能信息诊断与监测。发表论文20余篇。杨梦雪(通信作者)，女，1990年生。燕山大学机械工程学院硕士研究生。王闯，男，1991年生。燕山大学机械工程学院硕士研究生。张文文，男，1981年生。燕山大学先进锻压成形技术与科学教育部重点实验室实验师。