龙门起重机金属结构的多目标动态优化

袁　媛　杨正茂　孟文俊

1.太原科技大学，太原，030024　　 2.北京理工大学，北京，100081



龙门起重机金属结构的多目标动态优化

袁媛1杨正茂2孟文俊1

1.太原科技大学，太原，030024 2.北京理工大学，北京，100081

针对龙门起重机金属结构动态特性的复杂性和非线性，综合考虑龙门起重机金属结构设计中尺寸参数及起升载荷的不确定性，利用参数化有限元模型和试验设计方法，在龙门起重机金属结构动态系统中，建立了设计变量和动态参数间的关系。通过运用非支配排序遗传算法(NSGA-Ⅱ)，寻求桁架梁尺寸及节间布置最优化方案，并满足低应力、高固有频率及轻量化的要求，在构建高精度的响应面近似模型的基础上，运用Monte-Carlo模拟技术对优化方案的鲁棒性进行了评价。结果表明，该优化方法有效地实现了龙门起重机的动态结构优化，显著提高了其设计质量和效率。

可靠性设计；近似模型；遗传算法；多目标动态优化

0　引言

起重机的金属结构起着承受各种载荷、牵引、走行和制动等重要作用，是决定起重机运行安全及动力学性能最为关键的组成部分，故提高桁架式龙门起重机的动态性能，进行动态优化设计具有显著意义[1]。文献[2]提出的建立在灵敏度分析基础上的结构动力学修改方法主要通过试探法寻找最优解，由于变量相互间的制约关系，故如果系统维数较高，则难以得到较好的结果。文献[3-4] 利用有限元系统的优化模块，对整机结构进行了动态优化，该方法虽然采用灵敏度分析使变量个数缩减，但该方法缺乏智能性，不仅计算空间较大，且效果不太好。文献[5]运用BP神经网络技术和遗传算法构建了塔式起重机结构系统的计算模型，并对其进行动态优化设计，但研究只是对结构固有频率进行了目标优化，没有对动应力、动刚度、动位移等动力学特性进行综合考虑，难以得到最优的设计方案。童水光等[6]运用BP神经网络与混合遗传算法相结合的优化方法，进行了门机支腿的动态优化设计，但忽略了设计变量波动的影响，由于违反约束条件，故最终可能导致最优解成为非可行解。

本文以桁架式门式起重机(简称门机)为例，考虑设计参数的不确定性因素影响，将可靠性作为约束条件，以门机最大动应力、最大动位移、弯曲动刚度等为性能指标，同时通过灵敏度分析确定合理的设计变量，通过试验设计建立高精度的响应面代理模型，在此基础上，利用NSGA-Ⅱ算法进行多目标优化，最后采用Monte-Carlo模拟(Monte-Carlo simulation, MCS)技术对动态优化结果的鲁棒性进行评价，从而得到鲁棒性较高的动态优化设计方案。

1　结构多目标优化方法

1.1门机金属结构可靠性和鲁棒性设计方法

在实际的工程设计中，6σ设计理念通常应用于完成结构的可靠性和鲁棒性设计。和传统的优化设计方法相比，6σ优化设计由于增加了目标和约束条件的标准差，故不仅能获得目标函数的最优解，且能降低目标函数对设计变量的敏感性。设χi为约束函数，6σ优化设计的数学模型为

(1)

式中，XL、XU分别为设计变量X的约束上下限；μX、σX分别为设计变量的均值和方差；μY、σY分别为目标响应的均值和方差。

设结构的基本变量(表征设计尺寸、材料属性及载荷等)由随机向量X=(X1,X2,…,Xn)组成，其联合概率密度为fX(X)，桁架式起重机系统的可靠性要求表示为

R=∬g(X)>0fX((〗X)dX=P{g(X)>0}

(2)

式中，g(X)为状态函数，表示系统的失效状态和安全状态，g(X)≤0为失效状态，g(X)>0为安全状态。

设E[g(X)]和var[g(X)]分别表示约束函数的均值和方差，基于一次二阶矩方法，可靠性指标β可定义为

(3)

当fX(X) 服从正态分布时，结构可靠度的一阶估计量为

R=Φ(β)

(4)

式中，Φ(·)为标准正态分布函数。

在实际应用中，一般很难确定约束函数的联合概率密度函数，常采用概率约束等价转换数值逼近方法，以下的确定型约束是通过任意分布参数的可靠性约束等价转化而来：

μgμ+γσgμ≤0

(5)

其中，γ为满足可靠性设计要求R的可靠性指标，若为6，则为6σ设计。

1.2门机金属结构优化设计流程

和确定性优化设计调用仿真次数相比，鲁棒性概率优化设计仿真次数要多很多，为了解决此类优化问题，并且考虑到计算效率和稳健性等因素，构造一个响应面代理模型成为关键[7]。起重机负载的响应函数及其灵敏度导数具有高度非线性、严重不连续等特征，故需要找到一个能去除数值噪声且精度较高的响应面模型。文献[8]利用基于二次奇函数的响应面法，建立了比较精确的近似模型，被广泛应用在结构优化问题中。

基于近似模型的起重机金属结构的多目标动态优化设计步骤如下(图1)：

(1)对龙门起重机金属结构进行有限元分析、建立并验证优化设计模型；

(2)通过选择适合的试验设计方法，确定构造模型用的样本数据；

(3)基于有限元分析软件确定系统在样本点处的响应值，并选择一个较精确的近似模型来拟合在样本点处的响应值，并评价响应面近似模型的有效性；

(4)综合运用非支配排序遗传算法和6σ可靠性设计方法，优化响应面近似模型，获取多个Pareto解；

(5)利用Monte-Carlo模拟技术，评价Pareto解的鲁棒性，如果不能满足优化设计的要求，返回步骤(4)；

(6)在满足可靠性要求的前提下，输出优化设计方案。

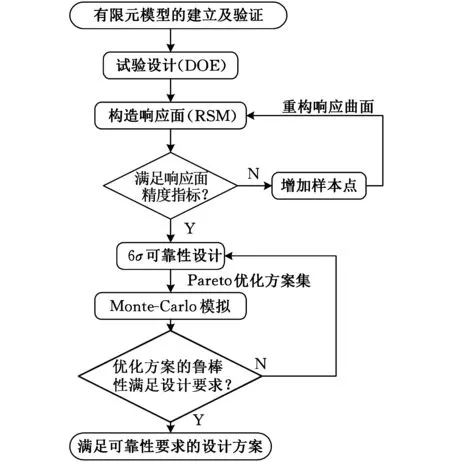
图1　起重机结构的多目标优化设计流程

2　结构动态优化模型的建立及验证

2.1动态优化模型建立

以某厂已生产的ME80t/38m龙门起重机为例，该门机金属结构属于典型的对称桁架结构，依据其结构形式及载荷特点，对该结构在ANSYS环境中进行空间建模。主要结构包括主梁2 根、下横梁2 个、支腿4个(其中刚性支腿2 个、柔性支腿2 个)，主梁属于桁架结构(由 4 个28b槽钢焊接而成)，支腿由空心圆管焊接而成。

选择3D梁单元BEAM189模拟门机金属结构。利用APDL构建门机结构有限元模型，其单元总数为664 469(其中四边形单元数为630 941，三角形单元数为26 710)[9]，如图2所示。

图2　整体有限元模型

2.2动态优化模型的验证

2.2.1门机金属结构应力分析

分析在满载情况下小车撞击支腿内侧的极端工况，如图3、图4所示，得出动应力、动位移分布及其最大值Δσmax(x)、Δχmax(x)，将Δσmax(x)和Δχmax(x)与对应的设计参数存入数据库。重复以上过程并将所得的样本数据存入数据库，为门机金属结构优化设计提供样本数据。

图3　门机满载等效应力云图

图4　门机满载位移云图

2.2.2门机金属结构模态分析

模态分析中，在门机的支腿底部添加全约束，选择Block Lanczos模态提取法计算门机结构模态，提取其前5阶模态频率和振型如表1所示。并求解出门机的二阶固有频率f2。

表 1　门机结构固有频率及振型运动趋势评价

从表1可推断，门机结构的全局弯曲和扭转模态频率基本一致，门机金属结构有限元模型的精度符合要求。

2.2.3门机金属结构灵敏度分析

设计灵敏度S为结构性能评价指标u(x1,x2,…,xn)对结构设计变量X=(x1,x2,…,xn)的偏导数(结构响应的梯度)，即

(6)

对于一个线性结构，其动力学方程为

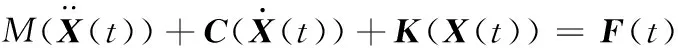
设λn和φn分别为结构的第n阶固有频率和振型，那么无阻尼结构自由振动的特征方程可表示为

(K-λnM)φn=0

(8)

通过式(8)的左右两端对第i项设计变量求偏导数得到模态(固有)频率对设计变量的灵敏度：

(9)

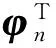
(10)

根据式(10)，得到刚度灵敏度为

(11)

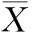
由式(11)可看到，灵敏度的值反映结构中的各个设计变量对结构性能的影响大小。为能够明确结构的薄弱部位及优化方向，进行灵敏度分析以忽略次要设计变量，可提高优化效率[10]。

弯曲动刚度是由二阶固有频率f2决定，并且是对门机动态性能影响最大的动态特性参数，所以本文只研究设计变量对评价指标f2的灵敏度，选取灵敏度变化较大的8个变量作为优化设计变量：X=[H1LA1A2A3EMpf]T，其值可以通过模态分析求得，如表2所示。

表2　设计变量对固有频率f2的灵敏度

2.3门机金属结构多目标动态优化模型

门机的稳定性和刚度主要由门机金属结构承担，在这种情况下，动应力、动刚度及整机结构振动等问题更加显著。若弯曲动刚度超过许用范围，则会引起整机结构的振动；若动应力超过最大值，则会使结构发生变形或损伤；若跨中动位移超过最大值，则会使结构产生失稳现象，因此，弯曲动刚度、动应力及跨中动位移就成为门机动态特性的关键性因素。

以小车起升载荷M和工作状态横向风压强度pf为两个约束条件，弯曲动刚度f2、最大动应力σmax和跨中最大动位移Ymax三个评价指标为目标函数，以桁架的高度H1、节间长度L、上弦杆横截面积A1、下弦杆横截面积A2、斜腹杆横截面积A3为设计变量的多目标优化问题如下：

(12)

式中，[σ] 为门机材料许用应力，MPa； [Y] 为顶部许用挠度，mm；[f2] 为二阶固有频率许用值，Hz；N0为约束条件的个数；NR为设计变量的个数。

式(12)中，根据设计规范和实际工况确定约束条件几何尺寸的上下限。当目标函数分别最接近各自许用值时，门机的设计方案最优。

3　多目标动态优化试验设计及响应面的

构建

对于非线性问题，采用最优拉丁超立方设计得到试验方案，进行30次采样，它改进了随机拉丁超立方设计的均匀性，使所有的试验点尽量均匀分布在设计空间，具有很好的空间填充性和均衡性，因而拟合的响应面模型更加精确真实。

由于各个设计参数的变化区间均不相同，个别参数的变化范围相差很大，故为了数据处理方便，对试验数据进行数据尺度归一化处理是很有必要的，即把试验方案中最小值和最大值的中点作为相位参考点，再将试验数据映射到-1～1范围之内进行处理。各设计变量的取值范围如表3所示。

表3　设计变量的取值分布区间

在构造响应面的同时，筛选代理模型的基函数，最终拟合得到响应面近似模型。各近似模型精度的评价指标如表4所示。

表4　试验设计检验参数表

4　多目标和可靠性设计优化求解

为保证得到的解具有均匀性和多样性，应使优化设计目标尽量收敛到真正的Pareto边界，本文采用NSGA-Ⅱ算法进行多目标优化。多目标优化得到的是多个最优解的集合，而不是唯一的全局最优解。

文献[12]指出：若进化代数超过1000，则NSGA-Ⅱ参数设置对计算结果的影响很小。本文对NSGA-Ⅱ参数进行设置：初始种群规模为10，进化代数为1200，交叉因子为0.9，交叉分布指数为18，变异分布指数为85。

假定各设计变量和约束条件服从正态分布，正态分布满足以确定性计算结果为均值，且变异系数(均方差和均值之比)为3%的条件。通过采用NSGA-Ⅱ遗传算法，迭代获得的多个可行的Pareto最优解如表5所示。

表5　部分可靠性Pareto最优解集

5　门机金属结构多目标优化设计结果评价

根据综合分析，4号方案具有较好的综合特性。为了评价设计变量的波动对目标函数响应的鲁棒性，通过采用Monte-Carlo抽样技术获得100组设计变量集合，把这些设计变量代入响应面近似函数中，目标函数响应的方差即可得到，该方差也就是设计变量的波动对目标函数响应的敏感度。4号方案的性能指标和原设计方案的对比情况如表6所示。

表6　原设计计算结果和可靠性优化设计解结果比较

6　结论

(1)提出了门式起重机动态多目标优化数学模型，最终由可靠性和鲁棒性验证所确定方案的合理性。

(2)在门机金属结构的多目标优化问题中，通过采用最优拉丁超立方试验设计方法，构建了相对简单的响应面近似模型以替代复杂的真实有限元模型，从而使迭代过程顺利进行。

(3)考虑弯曲动刚度、最大动应力、最大动位移等关键指标要求，在门机结构的多目标动态优化过程中，通过采用非支配排序遗传算法进行6σ可靠性优化设计，获得多个可靠性Pareto最优解集，对门机选择各种钢板提供了可靠的依据。

(4)研发了基于NSGA-Ⅱ算法的整机结构优化设计方案，使设计变量和约束条件全部落在可行范围内，使得响应目标波动较小，且具有良好的鲁棒性。

[1]MengWenjun,YangZhengmao,QiXiaolong,etal.ReliabilityAnalysis-basedNumericalCalculationofMetalStructureofBridgeCrane[J].MathematicalProblemsinEngineering, 2013, 2013 (5):1-5.

[2]齐丕骞,张凌霞. 基于灵敏度分析的结构动力模型修改[J]. 航空学报,1992,13(9):472-475.

QiPiqian,ZhangLingxia.StructuralDynamicModelUpdatingBasedonSensitivityAnalysis[J].ActaAeronauticaetAstronauticaSinica，1992,13(9):472-475.

[3]LiuXuemei,ZhangXiaoHui,YuanJin.RelevanceVectorMachineandFuzzySystemBasedMultiobjectiveDynamicDesignOptimization:ACaseStudy[J].ExpertSystemswithApplications,2010,37(5):3598-3604.

[4]PanJin,WangDeyu.TopologyOptimizationofTrussStructurewithFundamentalFrequencyandFrequencyDomainDynamicResponseConstraints[J].ActaMechanicaSolidaSinica,2006,19(3):231-240.

[5]于兰峰, 王金诺. 塔式起重机结构系统动态优化设计[J]. 西南交通大学学报,2007,42(2):206-210.

YuLanfeng,WangJinnuo.DynamicOptimumDesignofTowerCraneStructures[J].JournalofSouth-westJiaoTongUniversity,2007,42(2):206-210.

[6]童水光,王相兵,钟崴，等. 基于BP-HGA的起重机门机动态优化设计[J]. 浙江大学学报(工学版)，2013，47(1):122-130.

TongShuiguang,WangXiangbing,ZhongWei,etal.DynamicOptimizationDesignforRigidLandingLegofCraneBasedonBP-HGA[J].JournalofZhejiangUniversity(EngineeringScience),2013,47(1):122-130.

[7]RaoRV,PatelV.Multi-objectiveOptimizationofHeatExchangersUsingaModifiedTeaching-learning-basedOptimizationAlgorithm[J].AppliedMathematicalModelling,2013,37(3):1147-1162.

[8]CarigKJ,StanderN,DoogeDA,etal.AutomotiveCrashworthinessDesignUsingResponseSurface-basedVariableScreeningandOptimization[J].EngineeringComputations,2005,22(1/2)：38-61.

[9]荆辉,杨正茂.基于ANSYS平台的装卸桥结构有限元分析[J].机械工程与自动化,2013(6):60-62.

JingHui,YangZhengmao.FiniteElementAnalysisofStructureforLoadingBridgeontheBasisofANSYS[J].MechanicalEngineering&Automation,2013(6):60-62.

[10]孟文俊,杨正茂, 李小博, 等. 满足可靠性要求的桥式起重机金属结构优化设计[J]. 起重运输机械,2013(12):39-43.

MengWenjun,YangZhengmao,LiXiaobo,etal.OptimizationDesigninMetalStructureofBridgeCranewithReliabilityRequirement[J].HoistingandConveyingMachinery,2013(12):39-43.

[11]吴震宇,陈建康,许唯临,等.岩质边坡稳定的体系可靠度分析及工程应用[J].四川大学学报(工程科学版),2008,40(2):32-37.

Wu Zhenyu, Chen Jiankang, Xu Weilin,et al. Systematic Reliability Analysis of Rock Slope Stability and Its Engineering Application[J]. Journal of Sichuan University(Engineering Science Edition),2008,40(2):32-37.

[12]Srinivas N, Deb K. Multi-objective Optimization

Using Nondominated Sorting in Genetic Algorith-ms[J]. Journal of Evolutionary Computation.1995,2(3)：221-248.

(编辑袁兴玲)

Multi-objectiveDynamic Optimization of Gantry Crane Metal Structure Systems

Yuan Yuan1Yang Zhengmao2Meng Wenjun1

1.Taiyuan University of Science and Technology,Taiyuan,030024 2.Beijing Institute of Technology,Beijing,100081

Focused on the complexity and highly nonlinearity of the structure dynamic characteristics in a gantry crane, considering the uncertainty of dimensional parameters and lifting loads in metal structure design of the gantry crane, a parametric finite element model and experimental design methods were used to establish the relations among the design variables and dynamic parameters of the gantry crane structure systems. The non-dominated sorting genetic algorithm (NSGA-Ⅱ) was used to find the layout optimization of the truss girder internode and their sizes, then the requirements of low-stress, high natural frequency and lightweight were met. On the basis of high-precision response surface approximation model, Monte-Carlo simulation technique was used to evaluate the robustness performance of the optimization program. The application results indicate that the dynamic structure optimization of the gantry crane may be effectively achieved, and the design quality and efficiency are evidently improved.

reliability design; approximate model; genetic algorithm; multi-objective dynamic optimization

2015-12-07

国家自然科学基金资助项目(51575370)；山西省科技攻关资助项目(20140321008-04)

TH21

10.3969/j.issn.1004-132X.2016.19.014

袁媛，女，1982年生。太原科技大学交通与物流学院博士研究生、讲师。主要研究方向为起重运输机械、物流设备及其系统自动化、机电液一体化系统控制等。杨正茂，男，1988年生。北京理工大学机械与车辆学院博士研究生。孟文俊(通信作者)，男，1963年生。太原科技大学机械工程学院教授、博士研究生导师。