变密度法在挖掘机动臂轻量化设计中的分析与应用

邓志勇，熊昌炯，洪　昊，吴　龙，5

（1.三明学院 机电工程学院，福建 三明 365004；2.机械现代设计制造技术福建省高校工程研究中心，福建 三明365004；3.绿色铸锻及其高端零部件制造福建省协同创新中心，福建 三明 365004；4.福建省铸锻零部件工程技术研究中心，福建 三明 365004；5.福建三明高新技术产业开发区博士后工作站，福建 三明 365500）

变密度法在挖掘机动臂轻量化设计中的分析与应用

邓志勇1，2，3，4，熊昌炯1，2，3，4，洪昊1，2，3，4，吴龙1，2，3，4，5

（1.三明学院 机电工程学院，福建 三明 365004；2.机械现代设计制造技术福建省高校工程研究中心，福建 三明365004；3.绿色铸锻及其高端零部件制造福建省协同创新中心，福建 三明 365004；4.福建省铸锻零部件工程技术研究中心，福建 三明 365004；5.福建三明高新技术产业开发区博士后工作站，福建 三明 365500）

基于多体动力学的基本原理，建立了挖掘机工作装置的刚柔耦合模型。动臂拓扑优化设计采用变密度法，以动臂重量最小化为目标函数，以动臂各单元的相对密度为设计变量，强度和刚度为约束条件。根据计算后得到的相对密度云图对动臂进行轻量化设计，优化后的动臂减重最高可达30.8%。对比分析了拓扑优化设计前后动臂在规定时间内动态应力应变曲线变化趋势，应力应变曲线显示优化后动臂的应力和位移均有小幅增大，但均在许用值范围内，结果表明该优化方法是可行的。

变密度法；多体动力学；刚柔耦合；轻量化设计

动臂是挖掘机的主要工作装置之一，它与斗杠共同支配挖斗对土壤的挖掘和装车等动作。动臂上端与机架相连，由多块钢板焊接成箱式中空结构，相对于斗杠（小臂）而言，其臂较长，结构尺寸较大，故又被称为大臂。挖掘机工作装置通常重量较大，其中，动臂重量可达整个工作装置的三分之一以上，较大的自重不仅使工作装置动作缓慢，原材料、加工成本相应增高，而且也影响到产品的油耗和排放等重要性能。

轻量化是目前一项比较成熟的工程技术，广泛应用于汽车车身和车架等优化设计之中［1-5］。挖掘机轻量化设计是根据市场对节能环保产品的需求，在满足挖掘机动态运行下结构可靠性和安全性要求的同时，降低其零部件的重量。合理的轻量化设计不仅能减少用材降低企业成本，而且还能有效降低油耗减少排放，从而为市场和社会提供更有效地节能产品，因此，挖掘机轻量化对节能减排具有非常重要的意义。许多学者和专业人员对挖掘机动臂、斗杠和挖斗等工作装置的结构可靠性和安全性进行了大量研究和分析。陈艳，苏琦和祖挥程等人运用ANSYS和ABAQUS等大型有限元软件，分析了动臂在典型危险工况下的静态应力和位移，指出了动臂容易失效的位置，并对设计后挖掘机动臂进行了结构安全校验［6-9］。蒋美华等人对挖掘机工作装置进行了静力分析，并结合实际使用中的容易破坏形式，指出了在制造和焊接加工中存在的问题，提出了选材、增加加强筋、提高焊接质量以及强化处理等改进措施［10］。向琴等人建立了动臂优化模型，以动臂体积最小为目标函数，以动臂箱式结构中的多个焊接板块厚度为设计变量，机械强度为约束条件，对组成动臂的各个钢板厚度进行优化设计，实现了动臂减重8.3%［11］。目前，大部分文献和研究主要集中于典型工况下的瞬态静力分析，而对挖掘机某个作业动作一段时间内连续的动态强度分析较少，分析的结果仅局限于对现有产品的结构和安全校验，涉及的轻量化设计研究不多，且主要是在保证安全的前提下对结构中的板厚大小进行分析和优化，因此轻量化的效果并不明显。

1　基于变密度法的动臂拓扑优化数学模型

变密度拓扑优化设计是采用有限元方法，将结构件划分为许多小单元，以每个单元的相对密度为设计变量，所有单元的相对密度值介于0和1之间。其中，0代表该单元被优化删除，1代表该单元保留，密度介于0和1之间的单元是一种相对模糊的拓扑结构［12］。当设定拓扑优化相对密度阀值时，低于该阀值的单元即被删除，保留下来的所有单元即为拓扑优化后的结构，这样，通过相对密度就可以实现动臂拓扑结构的轻量化设计。采用变密度法对挖掘机动臂拓扑优化设计需要考虑3个基本要素：目标函数、设计变量和约束条件。以动臂重量最小化为目标函数，以动臂各单元的相对密度x为设计变量，强度和刚度为约束条件，因此，动臂的拓扑优化数学模型可表达为［13］：

动臂质量最小化：

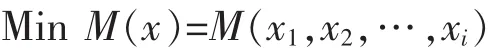
式中：M为动臂的质量，xi为动臂单元第i个相对密度值。

动臂拓扑优化的约束条件：

（1）强度条件（强度要求动臂工作时能承受相应的动载荷，根据文献［11］选择挖掘机动臂强度安全系数为1.8）：h1（x）=σj（x）-［σ］≤0 1.8

式中：σj（x）为动臂第j个单元的应力值；［σ］为动臂钢板的许用应力值，其钢板材料为16 Mn，许用应力值为345 MPa。

（2）刚度条件（要求动臂钢板最大变形量δ（x）不大于其许用变形量［δ］，其中，［δ］=15 mm［11］）:

2　工作臂刚柔耦合有限元分析

2.1工作臂刚柔耦合多体动力学模型的建立

某挖掘机工作臂有限元结构如图1所示，该工作臂臂长约7.674 m，总重1888.958 kg，采用六面体单元划分网格，网格单元总数量为102689个，钢板材料为16 Mn，密度为7800 kg/m3，弹性模量为2.08×1011Pa，泊松比为0.3。工作臂主要由3部分组成：上支臂（动臂），下支臂（斗杠）和挖斗。其中，前上支臂重量为655.207 kg，它由两个支撑固定，其通过上支臂控制器1和2推动下支臂绕上支臂左端连接轴做一定幅度的转动，上支臂模型如图2所示；同样，下支臂通过下支臂控制器1和2推动挖斗控制连接杆、控制臂连接杆，使挖斗绕下支臂左端连接轴做一定幅度的转动，从而实现挖斗的挖土运动。工作臂刚柔耦合有限元模型如图3所示，设置上支臂拓扑结构类型为PFBODY（即柔性体，如图3中白色线条轮廓所示），根据变密度法原理可知，轻量化设计过程中，在约束条件允许的范围内，柔性体的相对密度可在介于0和1之间变动，从而将上支臂设置为待优化的目标；设置其余9个构件的拓扑结构类型为PRBODY（即刚性体），刚性体相对密度为常数1，在轻量化设计中也参与多体系统运动，但拓扑结构不改变。

图1　挖掘机工作臂有限元结构

图2　上支臂（动臂）有限元结构

图3　挖掘机工作臂刚柔耦合模型

2.2约束和载荷的设定

模型中各构件连接和运动约束情况如下：该工作臂由10个构件连接而成，下支臂控制杆1与下支臂控制杆2之间、上支臂控制杆1与上支臂控制杆2之间沿各自轴心线分别设置1个移动副，限制其余5个自由度，模型中约束的设置如图3中的TRANS符号所示；挖斗与挖斗控制连接杆、挖斗与下支臂、下支臂与控制臂连接杆、挖斗控制连接杆与控制臂连接杆和下支臂控制杆1、下支臂与下支臂控制杆2、下支臂与上支臂控制杆1、上支臂与下支臂、上支臂与上支臂控制杆2之间分别设置绕Z轴的转动自由度，即设置相互连接的两构件绕它们之间转动轴轴线的转动自由度，限制其余5个自由度，模型中设置的销轴连接和约束分别如图3中的RBE2和REV符号所示；构件上支臂支撑限制了上支臂所有自由度。

由于挖掘机工作臂连续工作载荷十分复杂，因此，许多文献通常选择特定的危险工况进行瞬态静力分析［6-10］。由于此次分析和研究的重点是变密度法在轻量化设计的应用，为了能实现连续载荷下动臂拓扑结构优化设计，对载荷做如下简化［14］：

（1）由于工作臂总重量达1.8 t，忽略了铲斗土壤的重量，分析中仅考虑工作臂的重力；

（2）从工作臂重力和液压缸扭矩的角度施加载荷。由于挖掘阻力与工作臂各构件重力、斗杠挖掘力和铲斗挖掘力共同形成平衡力矩，故只需施加工作臂重力和挖掘力即可；

（3）忽略了斗杠挖掘力和铲斗挖掘力单独作业的情况。挖掘力来自上下支臂控制器的液压缸，可分为斗杠挖掘力（由上支臂控制器的液压缸驱动产生）和铲斗挖掘力（由下支臂控制器的液压缸驱动产生），通常是斗杠液压缸和铲斗液压缸的共同作用的合力，故着重分析复合作用下的挖掘力；

（4）挖掘机工作分析有许多方面，如工作臂运动分析，挖掘作业分析、挖掘阻力分析、起重作业分析、回转分析和装车作业分析，整个连贯作业的周期约10 s左右，此次只进行挖掘动作分析，时间约为1 s。

载荷设置步骤如下：首先，选择工作臂所有构件并创建重力卡片GRAV，完成工作臂重力的设置，并施加于工作臂上；挖掘机工作时，挖掘力的设置通过液压缸来实现，参考文献14设置复合挖掘力，即斗杠挖掘力和铲斗挖掘力共同作用产生挖掘力，创建控制卡片，编写相关程序，设置液压缸驱动下支臂控制杆1和上支臂控制杆1同时以v=0.5×T（0≤T≤1s，时间T的步长为0.01s）的速度沿各自轴心线分别推动挖斗控制连接杆和下支臂，这样使得挖斗绕下支臂旋转摆动并相应产生力矩，从而完成挖斗的挖掘动作。

2.3动臂拓扑优化目标函数的设置

以挖掘机上支臂设计域的重量最小为优化目标函数，上支臂中各单元的相对密度为设计变量，上支臂许用应力值和变形值为约束函数（目标函数、设计变量和约束函数的公式和数值见第2节动臂的拓扑优化数学模型之中）。将目标函数、设计变量和约束函数分别输入软件的objective、responses 和dconstraints模块中，完成动臂拓扑优化的前处理环节后，运行后处理器开始运算。

3　优化前后结果分析

3.1动臂拓扑结构的优化设计

采用变密度法拓扑优化后，动臂相对密度分布情况如图4所示，彩色云图中蓝色部分的密度值较低，红色部分的密度值较高，根据变密度法的基本原理，在红色条纹轮廓清晰明显的情况下，充分考虑柔性体拓扑结构的传力路径和基本结构后，可去除蓝色部分的实体结构，优化后的拓扑结构如图5所示，上支臂的主要4个表面都在不同程度上进行对称的开孔和挖槽，据此去除动臂钢板上相关实体材料，重新建立有限元模型，最终优化后的动臂实体结构如图6所示。分析结果显示，拓扑优化根据设置的目标函数、约束函数和最佳传力路径，动臂重量可由 655.207 kg最多减小到453.383kg，减重最高可达30.8%。

图4　挖掘机工作臂拓扑结构相对密度分布情况

图5　拓扑优化后的工作臂拓扑结构

3.2动臂优化前后连续动态结构分析

为了便于对比动臂优化前后的应力和位移动态变化情况，统一设置有限元云图中彩色条纹对应的数值区间，设置应力条纹区间为-2.2～2.2 MPa，位移条纹区间为0～1.720 mm。动臂优化前von Mises应力分布情况如图7所示，该图显示的是0.07 s时刻，即动臂的动态最大von Mises拉应力和压应力达到极值时刻时的整体应力分布情况，图中左边显示的是整体视图，右边为局部放大视图，从右边的局部视图可知在0.07 s时刻动态vonMises拉压应力极值出现在动臂与动臂液压缸连接座前后，数值大小分别为16.23和-12.47 MPa。如图8所示，拓扑优化后，动臂在0.12 s时刻动态最大von Mises拉应力和压应力达到极值，位置出现在动臂上部和侧边钢板的边缘，数值大小分别为20.73和-18.87 MPa。图9和图10显示的是在设定的连续工作时间内，优化前后动臂动态最大von Mises拉应力和压应力动态变化对比情况，从这两个图可以看出，虽然动臂优化后的最大von Mises拉应力和压应力整体曲线数值均比优化前略有增大，但其中的极值20.73和-18.87 MPa均小于之前参考设定的许用应力191 MPa，更重要的是通过优化已实现了动臂的轻量化目标。

图6　拓扑优化后的动臂实体结构

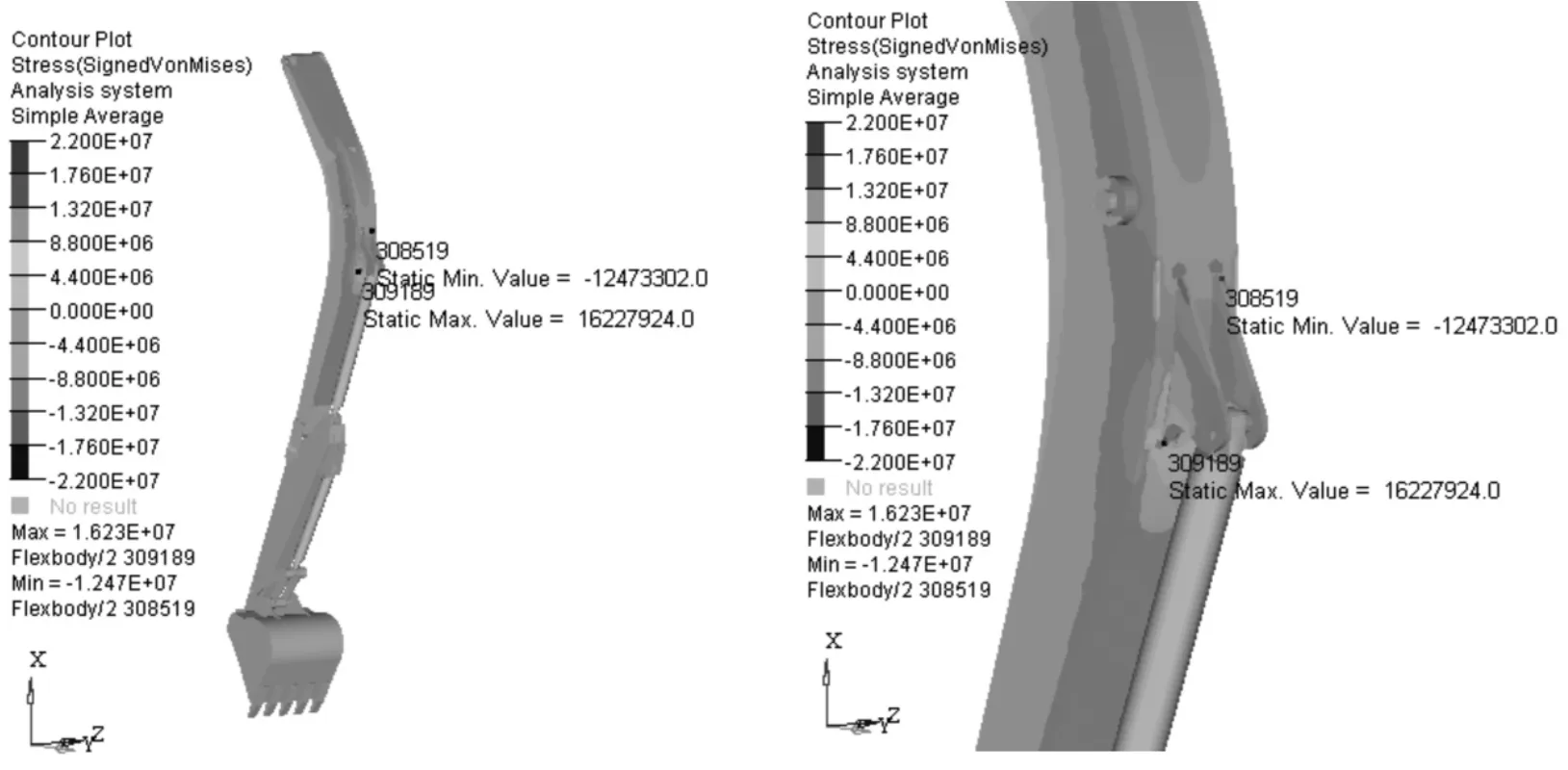
图7　拓扑优化前0.07s时刻动臂的von Mises拉压应力云图

图8　拓扑优化后0.12s时刻动臂的von Mises拉压应力云图

图9　优化前后动态最大von Mises拉应力对比

图10　优化前后动态最大von Mises压应力对比

图11显示了拓扑优化前动臂在0.1 s时刻动态最大位移达到极值时的位移分布云图，从该图右侧的局部视图可知，极值位移出现在动臂与斗杠连接的部位，动态最大位移值为0.915 mm；图12显示了拓扑优化后在0.14 s时刻动态最大位移达到极值时的位移分布云图，位移极值出现部位与优化前相同，动态最大位移值为1.720 mm。图13是工作时间区间内，优化前后动臂动态最大位移对比情况，从图中可以看出优化后动臂动态最大位移略有增大，但同样小于之前设定的许用位移15mm。

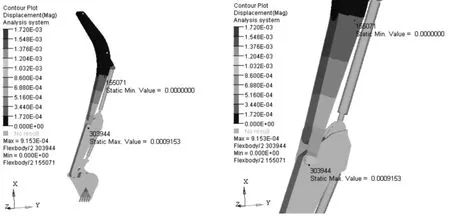
图11　拓扑优化前0.1s时刻动臂的位移云图

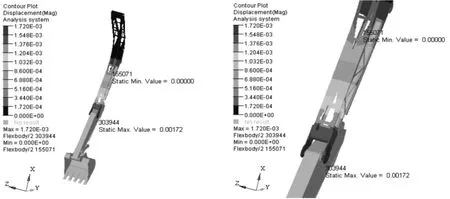
图12　拓扑优化后0.14s时刻动臂的位移云图

4　结论

轻量化设计不仅能大幅减轻动臂的重量，减少耗材降低成本，而且还达到节能减排的目的。在相同动力源下，减重后的动臂操作和作业将更加灵敏，工作效率得到提高，因此轻量化设计是提升挖掘机产品性能和产品竞争力的一个重要方法。在设定的工作时间区间内，建立刚柔耦合多体动力学模型，对比分析了拓扑优化前后动臂的动态应力应变，研究结果表明：

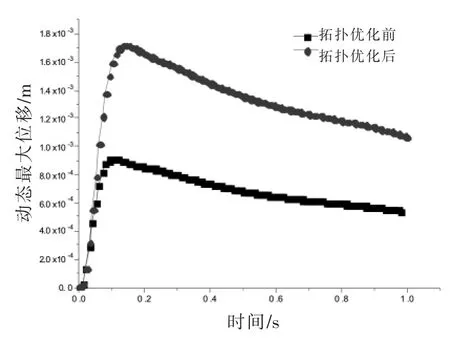
图13　拓扑优化前后动臂动态最大位移对比

（1）基于变密度法的轻量化设计是可行的。采用变密度法的拓扑优化设计能计算出动臂良好的传力路径，在设定的约束条件下，计算得到的相对密度云图能快速为轻量化设计提供可靠的指导和参考，避免了人工优化设计的盲目性。虽然拓扑优化设计后的动臂动态最大von Mises拉应力和压应力整体曲线数值均比优化前略有增大，极值为20.73和-18.87 MPa，但均小于16 Mn的参考许用应力191 MPa，位移也在许可范围之内，极值应力和位移分别出现在动臂和斗杠液压油缸连接处、动臂和斗杠连接处，分析中比较有意义的是理论上动臂重量由655.207 kg最多可减小到453.383 kg，减重最高可达30.8%。

（2）刚柔耦合多体动力学模型的建立进一步完善了以往常用的瞬态静力分析。以动臂为柔性体，工作臂其余9个构件为刚性体，并结合软件多体动力模块，建立了包括动臂在内的整个工作臂结构动力学模型，可对动臂在参考设定时间区间内进行动态连续有限元分析。

［1］吴卫枫，唐程光，鲁后国，等.车身轻量化设计过程方法介绍［J］.汽车工艺与材料，2015（4）：6-11.

［2］付俊岩，王伟哲，杨雄飞，等.汽车用铌微合金化钢板［M］.北京：冶金工业出版社，2006：27-28.

［3］方炬，关键鑫.轻量化与轻金属材料应用［J］.中国金属通报，2011，25：18-21.

［4］杨潘.液压成形技术在汽车轻量化中的应用［J］.冲模技术，2009（5）：15-18.

［5］杨志军，陈新，单圣涤，等.工程索道可变结构静力学拓扑优化方法研究［J］.矿山机械，2008，36（17）：41-45.

［6］陈艳，史青录，钟飞.300t大型液压挖掘机动臂和斗杆有限元分析［J］.工程机械，2015，46（1）：19-26.

［7］苏琦，赵宏强，王焜，等.挖掘机工作装置的静强度仿真分析［J］.计算机仿真，2014，31（11）：198-202.

［8］祖挥程，张志军，王浩丞，等.挖掘机工作装置有限元分析［J］.沈阳理工大学学报，2014，33（6）：60-64.

［9］蒋小利，江志刚，张华，等.基于ABAQUS的液压挖掘机动臂有限元分析［J］.现代制造工程，2014（8）：109-113

［10］蒋美华，苏俊刚，陈欣，等.液压挖掘机斗杆有限元静力分析［J］.工程机械，2012，43：40-43.

［11］向琴，张华，胡晓莉，等.基于ANSYS和神经网络的液压挖掘机动臂轻量化设计方法研究［J］.机床与液压，2015，43 （1）：136-140.

［12］张晓丽，李明鹏，李跃华，等.桥式起重机主梁腹板结构拓扑优化设计［J］.重庆工学院学报，2007，21（4）：30-32

［13］张积洪，杜阳.机场货运平台车快速拖车举升结构设计与仿真［J］.机械设计，2013，30（7）：92-96.

［14］洪清泉，赵康，张攀，等.OptiStruct&HyperStudy理论基础与工程应用［M］.北京：机械工业出版社，2014：235-241.

（责任编辑：朱联九）

Analysis and Application on Variable Density Method in the Process of the Excavator Boom Lightweight Design

DENG Zhi-yong1，2，3，4，5，XIONG Chang-jiong1，2，3，4，5，HONG Hao1，2，3，4，5，WU Long1，2，3，4，5，6

（1.School of Mechanical and Electronic Engineering，Sanming University，Sanming 365004，China；2.Engineering Research Center of Mechanical Modern Design and Manufacture in Fujian Province，Sanming 365004，China；3.CollaborativeInnovationCenterofGreenCasting-forgingIndustryandHigh-endPartsinFujianProvince，Sanming365004，China；4.Engineering Technology Research Center of Casting-Forging Parts Manufacturing in Fujian Province，Sanming 365004，China；5.Post-doctoral Research Station of Fujian Sanming High-tech Industrial Development Zone in Sanming，Fujian Province，Sanming 365500，China）

Based on the principle of multi-body dynamics，the rigid-flexible coupling model of excavator working device is established.Topology optimization design on boom is performed by the method of variable density design，with the boom weight minimization as the objective function，strength and stiffness as the constraint conditions.Lightweight design is implemented in the boom based on the relative density contours calculated，so the weight reduction of the boom optimized can be up to 30.8%.Within the specified time，the trends on dynamic stress-strain curve between the optimized boom and the original boom are compared and analyzed，the stress-strain curve indicates that stresses and displacements of the optimized boom are slightly increased，but they are within the allowable range of values，the results show that the optimization method is feasible.

variable density method；multi-body dynamics；rigid-flexible coupling；lightweight design

TU621

A

1673-4343（2016）02-0066-08

10.14098/j.cn35-1288/z.2016.02.011

2015-11-28

三明学院科研基金项目（CB201003/Q）；中国博士后科学基金资助项目（2013M541851）；福建省科技厅高校产学合作重大项目（2012H6018）；福建省自然科学基金资助项目（2012J01232）；福建省高校新世纪优秀人才支持计划资助项目（JA13290）

邓志勇，男，福建建瓯人，讲师，博士研究生。主要研究方向：汽车结构与安全。