大规模定制模式下基于梯形直觉模糊信息的多属性产品生产指派问题研究

程德通，李登峰

（1.三明学院 管理学院，福建 三明 365004；2.福州大学 经济与管理学院，福建 福州350116）

大规模定制模式下基于梯形直觉模糊信息的多属性产品生产指派问题研究

程德通1，李登峰2

（1.三明学院 管理学院，福建 三明 365004；2.福州大学 经济与管理学院，福建 福州350116）

运用梯形直觉模糊数建立基于顾客个性化属性需求值与企业属性输出值相对偏差的顾客满意度目标函数以及企业利润目标函数，并据此构建了一个多目标生产指派整数规划模型。该模型在采取个性化定制和个性化定价策略的基础上，不仅兼顾企业与顾客双方的利益，综合考虑企业生产能力和成本限制以及顾客权重和属性偏好等因素对生产安排的影响，而且在数据上采取梯形直觉模糊数分析大规模定制生产指派过程中遇到的模糊不确定信息，因而更加符合实际情况。应用实例说明生产指派模型的求解过程及其有效性、合理性。

大规模定制；梯形直觉模糊数；生产指派；优化模型；多目标决策

随着人们生活水平的提高以及市场竞争的日益激烈，顾客在选择产品时要求企业能够以较低的价格及时提供满足个性化需求的产品，而传统的大规模生产模式和完全定制生产模式已无法实现这一目标。大规模生产模式向顾客提供“标准化”的单一品种，忽略了顾客的个性化、差异化需求；完全定制生产模式虽然满足了顾客的个性化需求，但由于其存在生产周期较长、价格高昂、服务的市场面偏窄等问题，从而使得企业在竞争中处于不利的地位。在新的竞争环境下，如何化解大规模生产背后隐含的高效率、低成本的要求与完全定制背后隐含的个性化要求之间的矛盾，就成为企业适应环境变化、实现可持续发展的一大难题。大规模定制生产模式的出现，为企业解决这一难题提供了有效途径。大规模定制是在高效率、大规模生产的基础上，通过产品结构和制造过程的重组，运用现代信息技术、新材料技术、柔性技术等一系列高新技术，以大规模生产的成本和速度，为单个顾客或小批量、多品种市场定制任意数量产品的一种生产模式［1］。由于大规模定制综合了大规模生产的低成本、高质量、短交货期以及完全定制生产满足顾客个性化、多样化需求的优点［2］，因而被认为是21世纪企业的主流生产模式。

大规模定制企业遇到的最大挑战是产品丰富化带来的成本增加。顾客当然期望所有的个性化要求均能得到满足，但是企业如果不顾自身资源和条件的限制，一味地迎合顾客的偏好、满足顾客的所有要求，由此将给企业带来巨大的风险。因此大规模定制企业必须根据企业现有的生产能力和成本等限制条件以及顾客的属性偏好和重要性程度，在兼顾企业和顾客双方利益的基础上，对生产采取合理的安排，进行有效的指派。生产指派问题已成为大规模定制企业亟待解决的重要决策问题。

在大规模定制生产指派问题研究方面，文献［3］从缩短时间和设计成本出发，应用案例推理技术对一种新的物料准备算法进行了研究；文献［4］以大规模定制产品的质量效用和成本之间的“效费比”最大为目标，建立了基于顾客需求驱动的产品优化配置模型。文献［5］以企业产出与顾客需求偏差最小为目标，在考虑企业生产能力和成本限制等约束条件以及顾客权重的前提下，建立了一个包括标准化生产和个性化生产的生产安排模型，忽略了对产品价格因素以及企业利润目标的分析。文献［6］以顾客单个属性个性化需求值与企业输出产品的定制属性值差距最小为目标，对企业如何合理地优化生产安排进行了探讨；文献［7］以顾客需求与企业产出之间“相对误差值”最小为目标，建立了多属性产品的生产指派优化模型；文献［8］以顾客满意度最大化为目标，建立了基于顾客对价格以及产出偏差满意度的多属性产品生产指派模型；但文献［6-8］没有对不同的个性化需求属性如何定价以及企业收益如何优化进行分析，同时也忽略了顾客的权重因素。文献［9］运用TOPSIS原理分析了属性值为直觉模糊数的生产指派问题；文献［10］以企业利润最大化为目标，建立了确定最优定制程度和产量的优化模型，该模型利用差别定价来合理诱导顾客的定制需求；文献［11］以顾客对产品的满意度以及企业利润最大化为目标建立了一个多目标规划模型，并对多顾客定单的选择性生产问题进行了分析；但文献［9-11］同样也忽略了顾客权重因素。

通过以上文献可以看出，现有研究大多以顾客个性化需求与企业产出偏差最小为目标建立优化模型，少有文献考虑顾客权重因素，部分研究没有考虑输出属性的成本因素以及个性化定价问题，有的则忽略了企业收益优化问题。另外，已有的多数相关研究所给出的决策信息是精确或确定的数值。然而在现实的指派问题中，由于人类思维的模糊性以及指派问题的复杂性和不确定性等原因，决策者在对指派问题的认知过程中往往存在不同程度的犹豫或表现出一定程度的知识缺乏，从而使得决策者很难或者根本不可能给出精确的数值，而是经常以一些模糊的、不确定的信息如梯形直觉模糊数等的形式给出［12-13］。由于梯形直觉模糊数包括隶属度、非隶属度和犹豫度三方面的信息，它比梯形模糊数在处理大规模定制生产指派过程中遇到的模糊不确定性信息方面更灵活、实用，因此运用梯形直觉模糊数解决大规模定制生产指派问题具有重要的理论意义与实用价值，但是目前尚未见到这方面研究的报道。本文在采取个性化定制和个性化定价策略的基础上，综合考虑企业生产能力和成本限制以及顾客权重和属性偏好等因素对生产安排的影响，运用梯形直觉模糊数建立兼顾企业利润和顾客个性化需求的多目标整数规划模型，并通过一个算例来说明模型的求解过程及其有效性、合理性。

1梯形直觉模糊数及其排序方法

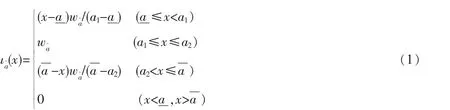
其非隶属函数为

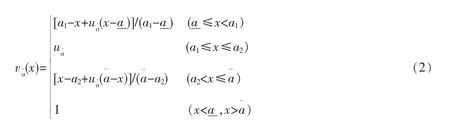
定义2［16］设为两个梯形直觉模糊数，γ≠0是任意实数。梯形直觉模糊数的加法、减法和数乘运算法则规定如下：

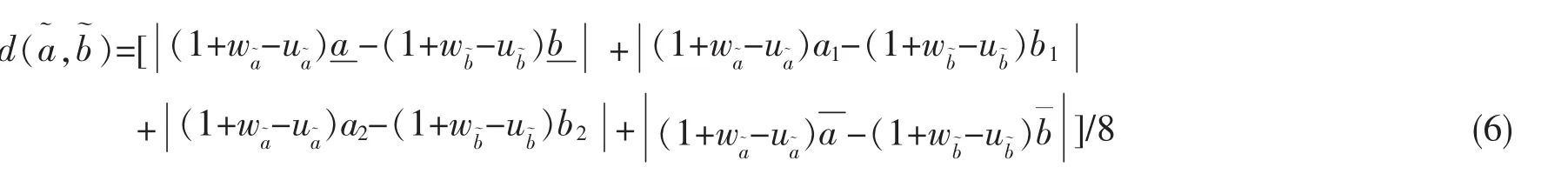
与

其关于隶属函数与非隶属函数的模糊度分别为

与

定义5［19-20］设˜是任意直觉模糊数。对于给定的λ∈［0，1］，记则分别称是直觉模糊数的加权均值和加权模糊度。其中，λ是权重函数，表示了决策者的信息偏好。λ∈［1/2，1］表明决策者喜欢肯定的、正面信息；λ∈［0，1/2］表明决策者喜欢否定的、负面信息。一般情况下取λ=0.5。

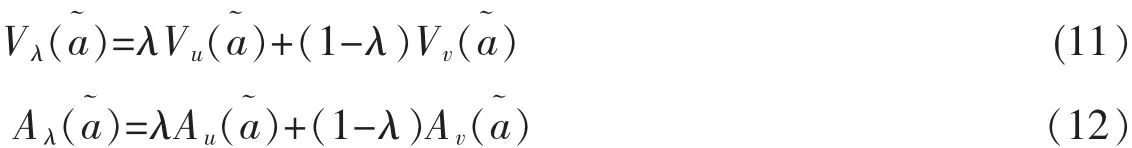
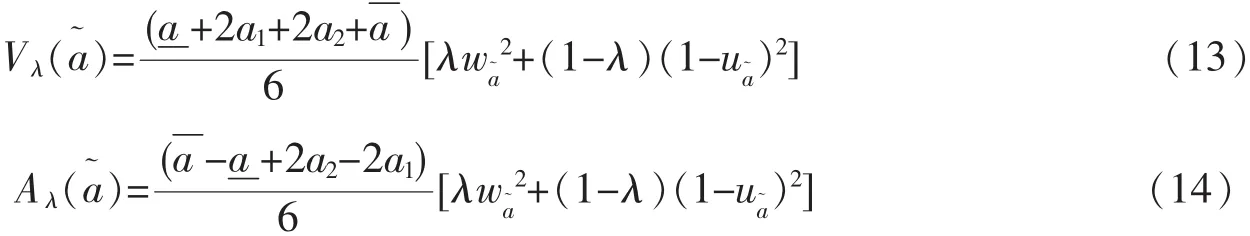
定义7［19，21］设为两个梯形直觉模糊数。规定其大小关系或排序如下：

2　模型的建立与求解

2.1顾客满意度目标函数

一个产品往往包含多种属性。产品属性包括物理方面的属性（如外观尺寸、速度、强度等）、功能方面的属性（如多功能、多组合、便携、可安装等）、经济方面的属性（如维护费用低、部件可换性等）等［22］，顾客会针对不同的属性需求选购产品。如购买一台手机，顾客会从外观尺寸、重量、像素、电池容量、屏幕分辨率、多功能、便携等等方面加以考虑，从而提出个性化需求。顾客对产品的个性化需求从本质上来说，也就是对产品的各个属性的需求［7］。顾客对产品的个性化需求可以通过模糊质量功能展开（QFD）方法［22］转化为产品属性，如顾客对手机高清拍照的需求，可以通过模糊质量功能展开方法转化为摄像头的技术属性，包括像素、广角和最大光圈等。假设有m个顾客，对某个产品的n个属性提出了个性化需求，这样就可以建立顾客的个性化属性需求矩阵为

不同的顾客对产品各个属性的偏好可能是不一样的。如对手机，有的顾客对摄像头的质量即能否高清拍照比较在乎，对外观不是很在意；有的顾客对电池容量即能否运行持久特别在意，而对其他属性要求则不高。因此，可用矩阵Wm×n表示m个顾客对产品n个属性的个性化需求偏好。

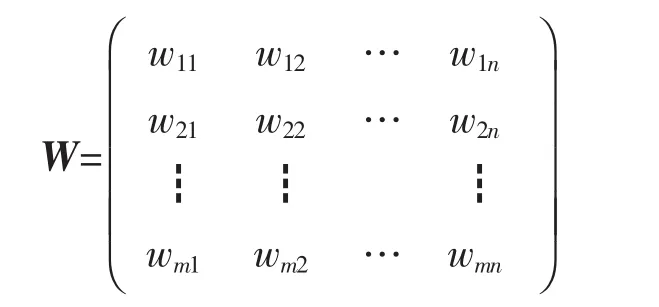
在矩阵W中，wij（i=1，2，…，m；j=1，2，…，n）表示第i个顾客对产品第j个属性的偏好，且满足

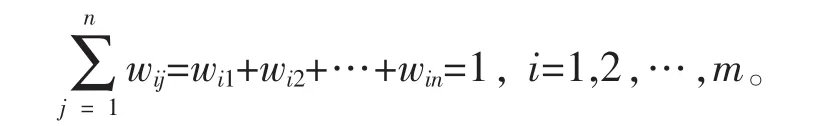
假设产品的n个属性由某大规模定制企业的n个分厂加工，即每个分厂负责产品一类属性的生产。假设属性之间的关系是独立的，因此分厂之间的生产也是独立的。假设第j个分厂，针对m个顾客对第j个属性的需求，下设tj个车间负责生产。通常情况下，由于企业资源及条件的限制和约束，tj应该小于m；反之，如果tj大于或等于m，则企业可以做到完全定制。由于有资源的限制，企业如果不顾自身的条件而直接采用完全定制，就会导致高成本、长交货期以及对市场的响应性明显降低，从而使得企业难以适应当今市场竞争的挑战。假设在一个生产周期内第j个分厂各车间生产能力的上限分别为Q1j，Q2j，…，Qtjj。

假设第j个分厂的tj个属性输出值可以用梯形直觉模糊数表示为y由于大规模定制不是完全定制，因此第i个顾客对产品第j个属性的个性化需求值与企业第j个分厂下的第k个车间的实际属性输出值可能会存在偏差，这个偏差可以用两个梯形直觉模糊数之间的Hamming距离d来表示。通常每一个顾客对这个偏差有一定的容忍度，定义第i个顾客对产品第j个属性输出偏差容忍度的极限值为顾客“最小不可容忍度”rij，即顾客对属性需求值与企业实际属性输出值的偏差在rij以内，可以接受；偏差超出rij，顾客不接受定制产品。假定m个顾客对产品n个属性输出偏差的“最小不可容忍度”可以用矩阵表示为

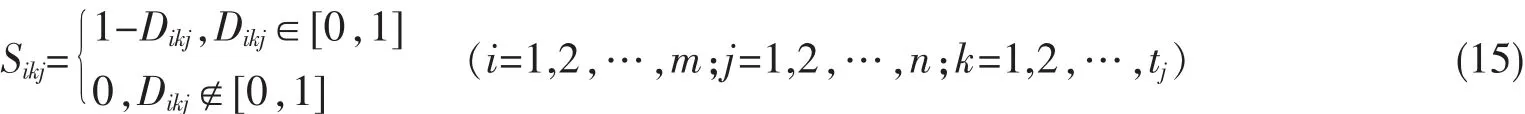
式中，Sikj表示第i个顾客对第j个分厂下的第k个车间的产品属性输出相对偏差的满意度。

由于不同的顾客为企业创造的价值是不一样的，因此对于企业而言，各个顾客的重要程度不尽相同。假设顾客的重要性程度用顾客权重向量G=（g1，g2，…，gm）来表示，其中gi表示第i个顾客的权重，且满足

综上所述，假设企业有生产能力的限制，各个分厂之间的生产相对独立，在综合考虑顾客的属性偏好和重要性程度等因素对生产安排影响的前提下，可以构建顾客满意度目标函数为

目标函数（16）表示企业以顾客对产品的满意度最大化为目标进行生产安排，使得产出最大限度地满足顾客对产品多种属性的个性化需求，即企业的个性化定制策略就是要最大限度地提高顾客对产品属性输出相对偏差的满意度。目标函数中变量zikj表示在第j个属性中，第i个顾客的个性化属性需求所对应的产品是否由第k个车间来生产，用表达式表示为

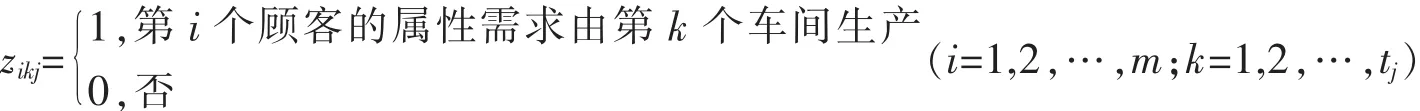
2.2企业利润目标函数

企业单位产品的利润取决于产品的价格与成本。假设企业各个车间实施独立的经济核算，产品属性成本的核算和价格的确定由各个车间提供。产品属性价格的确定应考虑顾客对产品属性输出相对偏差的满意度，通常情况下，企业产品输出属性的相对偏差越小、顾客对个性化需求属性的满意度越高，愿意支付的价格也就越高。假设顾客满意度为100%时愿意支付的属性价格用梯形直觉模糊数表示为P˜ij0。由于不同顾客对产品属性的需求具有差异性，因此从定价策略来讲，企业可以在综合考虑顾客支付意愿与产品属性成本的基础上，针对不同的顾客属性需求制定不同的价格，即对顾客的属性需求采取个性化定价策略。通过实施个性化定价策略可以确定产品属性合理的价格水平从而实现合理地诱导顾客需求的目的。企业可构建输出属性的个性化定价模型为

综上所述，假设企业各个车间采取独立的经济核算，可以根据产品的属性价格以及成本，在充分考虑顾客权重和属性偏好的前提下，构建利润目标函数为

目标函数（18）表示企业通过合理安排生产，使得为所有顾客加工的产品属性利润之和即总利润最大化。目标函数中变量zikj为0-1变量，其具体含义与式（16）中的zikj相同。表示第j个分厂下的第k个车间为第i个顾客提供的单位产品属性价格与单位产品属性成本的Hamming距离，其经济含义为单位产品属性利润。

2.3生产指派优化模型

大规模定制模式追求的是企业与顾客的双赢，因此，可在顾客满意度目标函数和企业利润目标函数，即式（16）和（18）的基础上，构建以顾客对产品的满意度最大化以及企业利润最大化为目标的生产指派优化模型，即

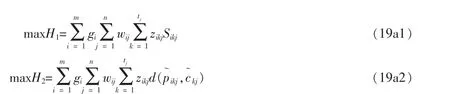
j

分别由式（15）与（17）计算得出，z

ikj

为0-1决策变量。

目标函数（19a1）与（19a2）表示该模型为兼顾顾客满意度和企业营利的双目标整数规划模型；约束条件（19b）表示顾客对产品某个属性的个性化需求值与企业实际输出值的偏差不能超过该顾客的最小不可容忍度；约束条件（19c）表示任何一个顾客的个性化属性需求所对应的产品只能且必须由负责该属性生产的分厂下的其中一个车间生产一次，该分厂下的其他车间不再进行生产；约束条件（19d）表示企业有生产能力的限制，在一个生产周期内某个车间进行某个属性加工的产品数量总和，不超过该车间生产能力的上限；约束条件（19e）表示为了保证采取独立核算的各车间的经济利益，企业提供给顾客的产品，其属性价格应高于属性成本；约束条件（19f）表示zikj为0-1决策变量。

2.4求解方法与步骤

为了求解双目标优化模型（19），先测算第i个顾客对第j个分厂下的第k个车间的产品属性输出相对偏差的满意度Sikj与车间相应可得利润的比值ωikj为

在式（20）的基础上，对全体ωikj进行平均，可求得算术平均数ω为

因此，以ω作为综合权重，可将式（19）的双目标模型转化为如下的单目标模型

模型（22）的指派问题是一个0-1型整数规划，在变量较少的情况下，可运用枚举法求解［23］；当变量数目较多时，可以使用专门的优化软件包如Lingo11.0等来求解。利用本文的定义7，可对约束条件（22e）的梯形直觉模糊数进行大小比较。需要说明的是，模型（22）的解是模型（19）的非劣解集中的一个非劣解，ω的取值会影响模型（22）的求解结果，在解决具体的大规模定制生产指派问题中，企业可以根据实际情况在综合考虑利润目标以及顾客需求等因素的基础上确定ω的取值方法，也可以根据问题的需要选用其他方法求解模型（19）。

综合前述内容，可将问题求解步骤归纳如下：

步骤1.根据式（15），计算顾客对企业产品属性输出相对偏差的满意度；

步骤2.根据式（17），测算企业各个车间为每位顾客确定的产品属性价格；

步骤3.根据式（16），建立顾客满意度目标函数；

步骤4.根据式（18），建立企业利润目标函数；

步骤5.根据式（20）与（21），确定综合权重；

步骤6.根据式（22a）-（22f），建立大规模定制模式下多属性产品生产指派的优化模型；

步骤7.求解优化模型（22），并进行生产指派。

3　算例分析

假设某大规模定制企业的某一类产品由3个产品属性组成，并分别由3个分厂进行生产。3个分厂下面分别有3、4、3个车间根据产品属性的生产要求进行加工，即t1=3，t2=4，t3=3。各分厂下设车间的产品属性输出值、成本以及生产上限均已知，相关数据见表1。

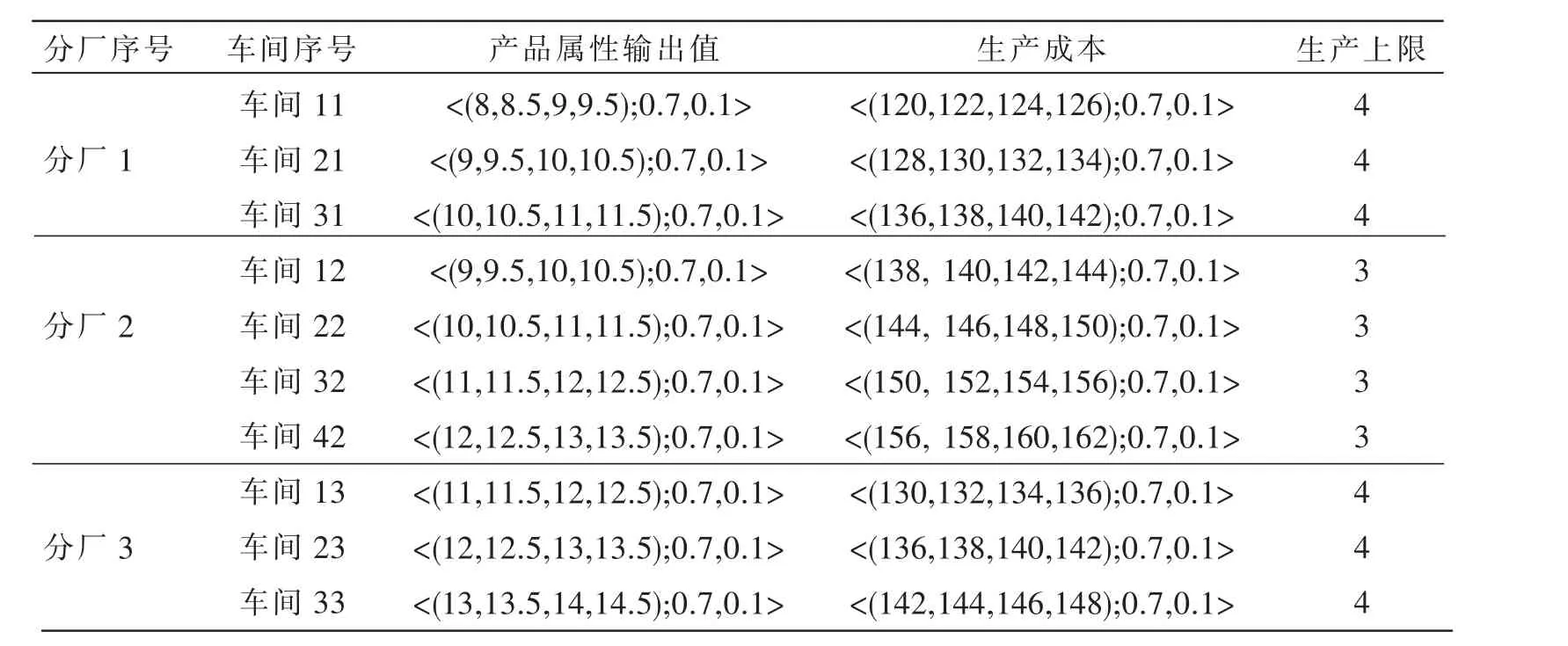
表1　各分厂下设车间的产品属性输出值、生产成本以及生产上限

假设在某一段时期有10个顾客对产品提出个性化需求，他们的属性需求值与属性偏好矩阵分别为

和

不同顾客对产品某个属性的个性化需求值与企业输出值偏差的容忍度是不相等的，这10个顾客对该产品3个属性偏差的最小不可容忍度用矩阵R表示为

顾客的权重向量为

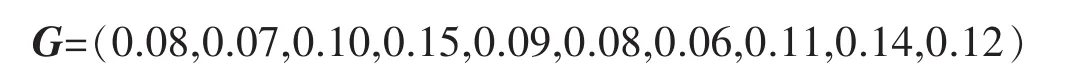
假设顾客在向企业提出个性化需求时，必须针对产品的3个属性提供满意度为100%时愿意支付的属性价格P˜ij0，相关数据如表2所示。

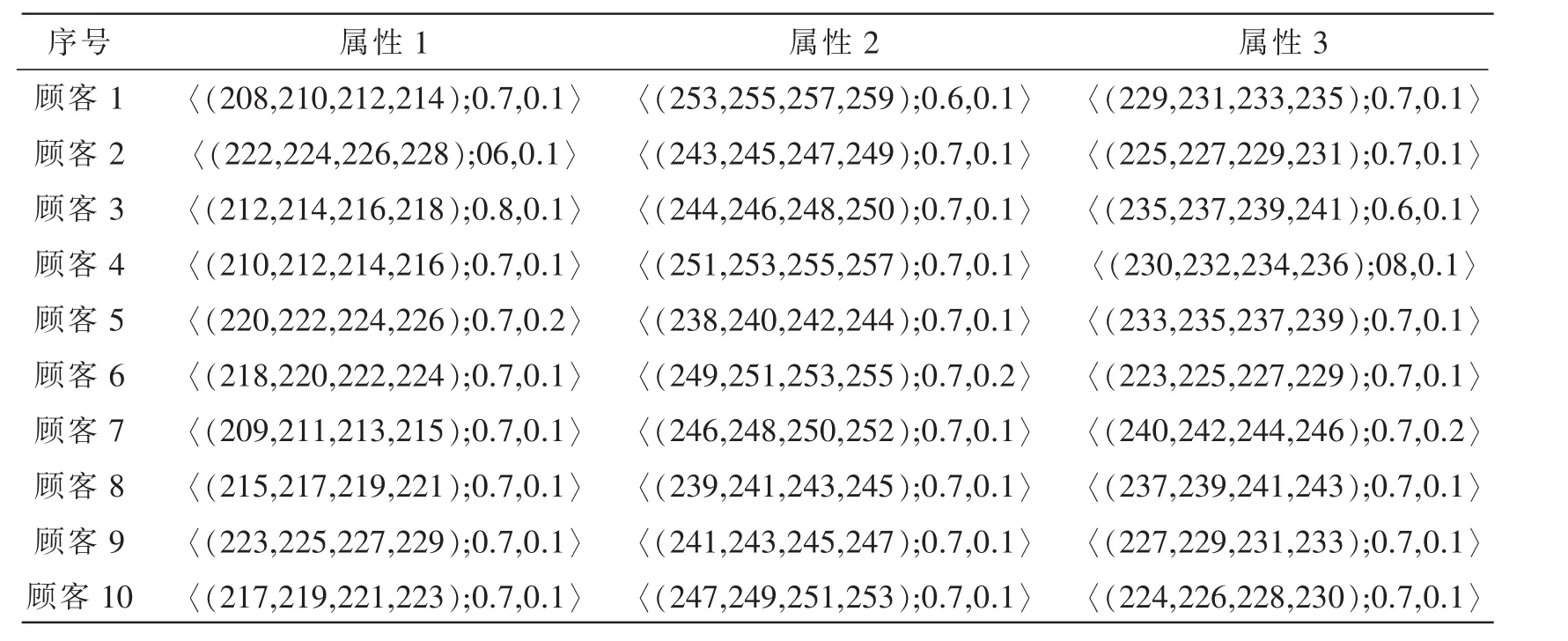
表2　顾客满意度为100%时愿意支付的产品属性价格

根据上述已知条件，现要求企业兼顾营利要求以及顾客对产品的个性化需求，并在综合考虑企业生产能力和成本限制以及顾客权重和属性偏好等因素的基础上，对生产进行指派。

根据步骤1～7，可建立大规模定制模式下生产指派的优化模型为

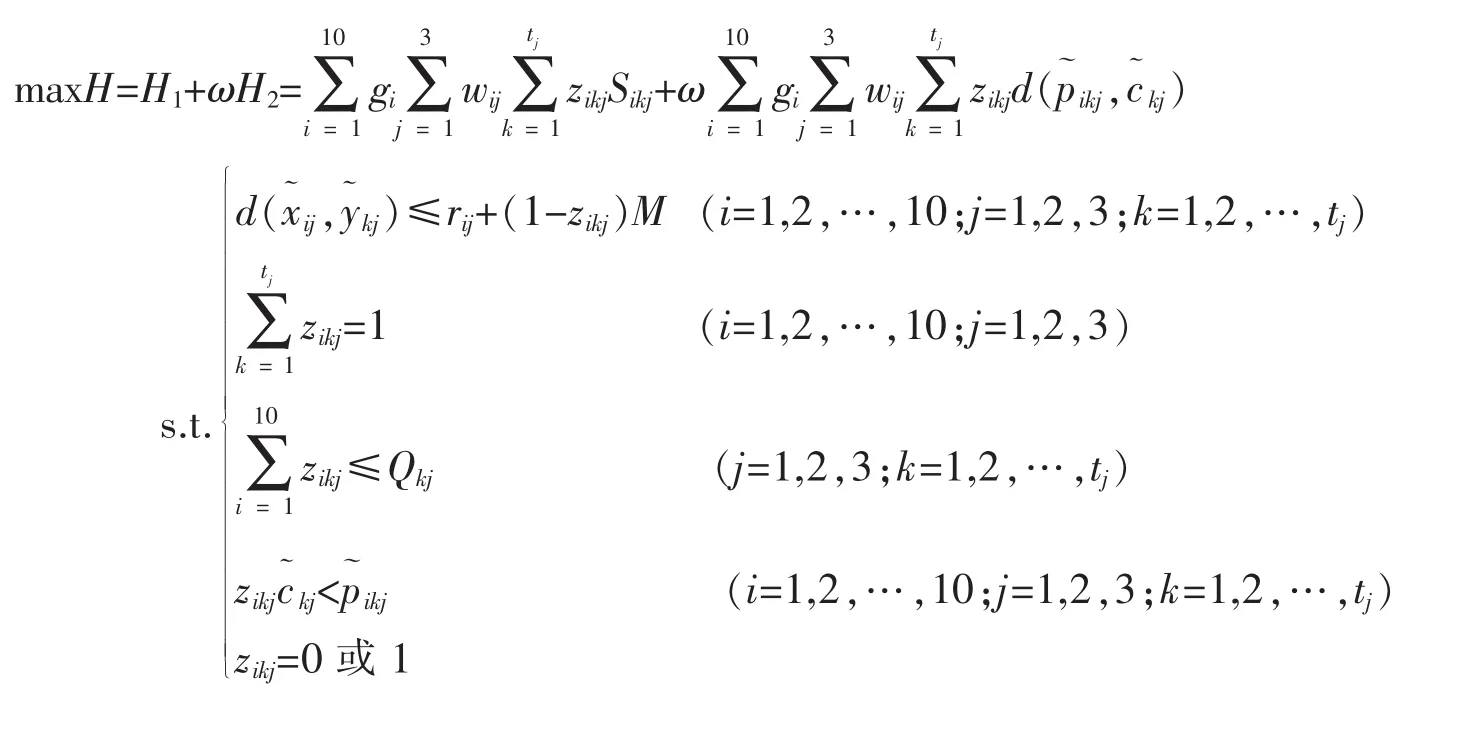
模型中，Sikj可由式（15）计算得出；p˜ikj可由式（17）计算得出；根据式（20）与（21），可确定综合权重ω= 0.014153。式中其余参数均已知，要求得出zikj的值。

上述生产指派问题是一个0-1型整数规划，本文采用Lingo11.0求解。经运算后，可以得到生产安排的结果，如表3所示。

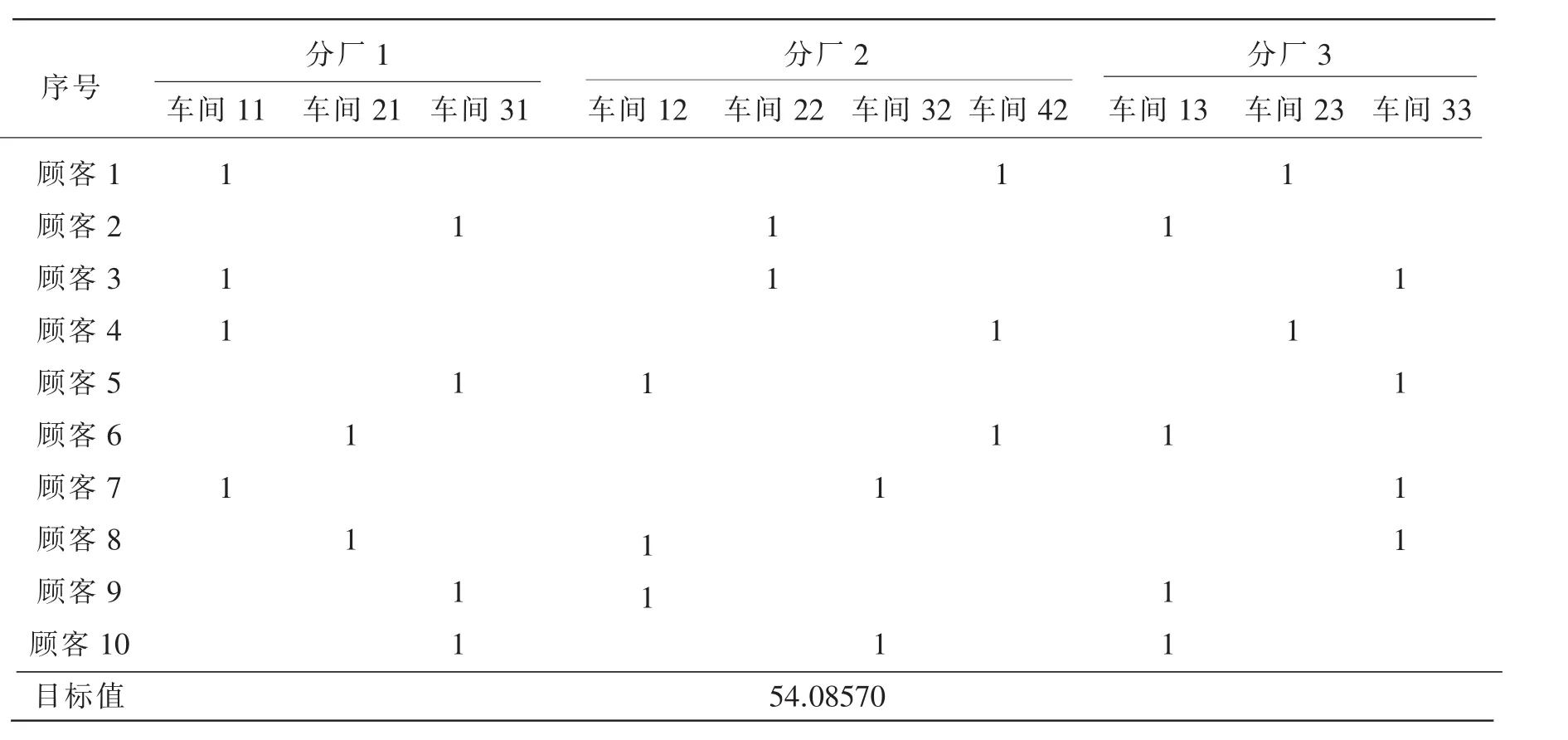
表3　生产安排的结果

4　与相关文献比较分析

文献［8］通过建立顾客对价格以及个性化属性需求与企业产出偏差值的顾客满意度函数，研究了大规模定制模式下的多属性产品的生产指派问题。在产品属性定价方面，文献［8］直接给出了产品各种属性的企业定价，也就意味着企业对不同顾客的相同需求属性制定相同的价格。因此文献［8］虽然考虑了价格因素，但没有针对不同顾客的具体定制需求分别制定不同的价格，即没有通过实施个性化定价策略去合理地诱导顾客的需求。其次，文献［8］以提高顾客满意度为目标建立规划模型，没有考虑企业利润这一因素，即仅考虑顾客的需求，忽略了企业的收益优化问题。再次，文献［8］没有考虑企业产品属性成本及其约束条件，也未考虑顾客权重对生产指派的影响。另外，文献［8］采用实数进行研究，没有考虑大规模定制模式下生产指派面临的模糊不确定性等问题。与文献［8］相比，本文对生产指派问题的分析，一是不仅考虑了顾客的个性化定制问题，而且给出了产品属性的个性化定价模型；二是兼顾满足顾客与企业双方的要求；三是综合考虑了顾客权重和属性偏好以及企业现有生产能力和成本的限制等因素对生产指派的影响；四是在数据上运用梯形直觉模糊数分析大规模定制生产指派过程中遇到的模糊不确定性信息，因而更加符合实际情况，对大规模定制企业更具指导和借鉴意义。

5　结论

本文在已有相关研究的基础上，探讨了大规模定制模式下属性值为梯形直觉模糊数的多属性产品生产指派问题。大规模定制企业必须一方面通过采取个性化定制策略最大限度地提高顾客对产品属性的满意度，另一方面通过采取个性化定价策略确定产品属性合理的价格水平、实现合理地诱导顾客需求的目的，即通过有效的个性化定制策略和个性化定价策略，兼顾企业和顾客两个决策主体的利益。通过本文的研究，可以帮助大规模定制企业制定有效的个性化定制策略和个性化定价策略，从而实现企业与顾客的“双赢”。同时，本文的研究成果也丰富了大规模定制模式下生产指派的研究内容，促进了梯形直觉模糊数在生产指派决策领域中的运用。

本文探讨的是大规模定制模式下属性值为梯形直觉模糊数的多属性产品生产指派问题。然而在现实的大规模定制生产指派问题中，属性值也可能会同时出现数值、区间数、不确定性偏好序、语言评价以及直觉模糊数等多种形式信息的情形。另外，本文未考虑产品的属性之间可能存在的关联性。这些问题将在后续的研究中进一步地予以探讨。

［1］邵晓峰，季建华，黄培清.21世纪的主流生产模式：大规模定制［J］.软科学，2000（4）：43-45.

［2］祁国宁，顾新建，谭建荣，等.大批量定制技术及其应用［M］.北京：机械工业出版社，2003：4.

［3］TSENG H E，CHANG C C，CHANG S H.Applying case-based reasoning for product configuration in mass customization environments［J］.Expert Systems with Applications，2005，29（4）：913-925.

［4］周春景，林志航，刘春涛.客户需求驱动的产品配置优化［J］.西安交通大学学报，2007，41（3）：339-343.

［5］贾国柱，程杨.基于顾客聚焦的生产安排模型及相关问题［J］.工业工程与管理，2006（4）：1-5.

［6］周俊，梁樑，余玉刚.基于顾客满意度最大化的生产指派问题［J］.管理工程学报，2004，18（4）：1-5.

［7］梁樑，刘晓伟，余玉刚，等.MC模式下多属性产品的生产指派问题［J］.系统工程学报，2004，19（2）：188-192.

［8］梁琛平，彭灿.MC模式下多属性产品的改进生产指派模型［J］.工业工程与管理，2009，14（3）：96-104.

［9］程德通，李登峰，余高锋.大规模定制模式下具有直觉模糊信息的生产指派问题研究［J］.数学的实践与认识，2015，45 （22）：92-106.

［10］王林，吴清烈.价格诱导下大规模定制的定制程度和产量优化［J］.统计与决策，2007（9）：50-51.

［11］梁樑，刘晓伟，朱晨，等.MC模式下基于多顾客定单的选择性生产问题［J］.系统工程与电子技术，2004，26（9）：1222-1225.

［12］徐泽水.直觉模糊信息集成理论及应用［M］.北京：科学出版社，2008：1.

［13］尤天慧，张尧，樊治平，等.信息不完全确定的多指标决策理论与方法［M］.北京：科学出版社，2010：65.

［14］李登峰.直觉模糊集决策与对策分析方法［M］.北京：国防工业出版社，2012：24-154.

［15］WANG J Q，ZHANG Z.Aggregation operators on intuitionistic trapezoidal fuzzy number and its application to multicriteria decision making problems［J］.Journal of Systems Engineering and Electronics，2009，20（2）：321-326.

［16］周晓辉，姚俭，吴天魁.基于梯形直觉模糊数的TOPSIS多属性决策方法［J］.上海理工大学学报，2014，36（3）：281-286.

［17］王坚强，张忠.基于直觉梯形模糊数的信息不完全确定的多准则决策方法［J］.控制与决策，2009，24（2）：226-230.

［18］万树平.直觉梯形模糊群决策的可能性均值方差方法［J］.系统工程学报，2012，27（6）：782-788.

［19］南江霞.梯形直觉模糊数排序方法及在多属性决策中应用［J］.经济数学，2014，31（3）：87-91.

［20］LI D F.A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems［J］. Computers and Mathematics with Applications，2010，60（6）：1557-1570.

［21］LI D F，NAN J X，ZHANG M J.A ranking method of triangular intuitionistic fuzzy numbers and application to decision making［J］.International Journal of Computational Intelligence Systems，2010，3（5）：522-530.

［22］岑咏霆.模糊质量功能展开［M］.上海：上海科学技术文献出版社，1999.

［23］《运筹学》教材编写组.运筹学［M］.北京：清华大学出版社，2005：122-132.

（责任编辑：朱联九）

Research on the Production Assignment of Multi-attribute Product Based on the Trapezoidal Intuitionistic Fuzzy Information under the Mass Customization Mode

CHENG De-tong1，LI Deng-feng2

（1.School of Management，Sanming University，Sanming 365004，China；2.School of Economics and Management，Fuzhou University，Fuzhou 350116，China）

Utilizing the tool of trapezoidal intuitionistic fuzzy number，the objective function of enterprise profit and the objective function of customer satisfaction based on the relative deviation between the demand values of customer personalized attributes and output value of enterprise attributes were built，and then the model of multiple-objective integer programming was constructed for the production assignment.This model was based on the personalized customization and personalized pricing.It involved some factors such as the benefits of customer and enterprise，the restriction of enterprise's producing capacity and cost，the effect of customer weight and attribute preference on production assignment.The tool of trapezoidal intuitionistic fuzzy numbers was used to dispose the fuzzy information in analyzing the process of production assignment in the background of mass customization in order to conform to reality.Some application examples were given to illustrate the solution procedure of the model and its effectiveness and rationality.

mass customization；trapezoidal intuitionistic fuzzy number；production assignment；optimized model；multi-objective decision making

F224.9

A

1673-4343（2016）02-0033-11

10.14098/j.cn35-1288/z.2016.02.007

2016-2-15

国家自然科学基金重点项目（71231003）；国家自然科学基金项目（71171055）

程德通，男，福建闽侯人，副教授。主要研究方向：决策分析、大规模定制。