制导炸弹俯仰通道自抗扰控制应用研究

张宇翔，宋金来，王明光，金岳

（北京航天微系统研究所，北京100094）



制导炸弹俯仰通道自抗扰控制应用研究

张宇翔，宋金来，王明光，金岳

（北京航天微系统研究所，北京100094）

针对俯仰通道的过载控制，提出了控制回路的自抗扰控制设计方法。俯仰通道具有不确定性，利用两个降阶线性扩张状态观测器对系统的不确定性进行实时估计并予以动态补偿，使控制对象化为“积分器串联型”，再设计比例控制。仿真结果表明，与PID相比，ADRC具有较强的抗干扰能力，以及较高的控制品质。

PID；自抗扰控制；线性扩张状态观测器；过载控制

0　引言

近年来，精确制导炸弹以其使用方便、精度高等特点越来越得到国内外用户的青睐。然而，由于制导炸弹使用空域较广，弹体动力学参数变化范围较大，被控对象具有较强的不确定性，因此，俯仰通道对控制回路的设计技术提出了较高的要求。原用PID控制策略通常采取变参数调节（增益调度）的方法，控制参数的确定往往通过大量的系统计算分析、仿真及实验获得，本质上只是一种试凑的方法［1］，将PID应用于制导炸弹控制回路存在一定的局限性。本文提出了将自抗扰控制（Active Disturbance Rejection Control，ADRC）应用于俯仰通道控制回路的方法，用于提高系统的抗干扰能力、降低控制回路设计的复杂度。

20世纪90年代，韩京清研究员提出并发展了自抗扰控制。该方法是将系统模型的不确定性与未知扰动予以实时估计并动态补偿，具有参数整定简便、抗干扰能力强等特点。近年来，已有学者开展了对ADRC的理论研究［2-5］，并应用于飞行控制系统设计，主要包括导弹、无人机的姿态控制及制导炸弹滚转通道控制等，取得了一些研究成果［6-9］。本文基于制导炸弹俯仰通道过载反馈控制设计，提出了用双线性扩张状态观测器（Linear Extended States Observers，LESO）对系统扰动进行实时估计与补偿，再通过线性控制实现对系统的闭环控制。

1　俯仰通道特性

俯仰通道过载控制的基本原理为：利用惯性仪表敏感到弹体的俯仰角速度ωz和法向过载ny，通过反馈控制形成舵机控制指令，驱动舵机运动实现对炸弹的稳定控制。

弹体纵向运动的主要方程［10］为：

其中，θ和γV为弹道倾角和速度倾斜角；ωx、ωy和ωz表示绕弹体坐标系旋转的滚转角速率、偏航角速率和俯仰角速率；Jx、Jy和Jz为弹体坐标下绕三个轴的转动惯量。Y、Z和Mz分别为升力、侧向力和俯仰力矩，并有：

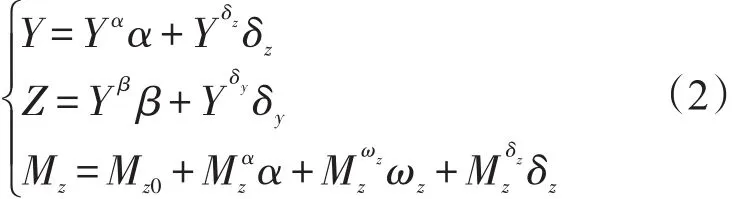
将式（2）中第三式代入式（1）中第三式，整理得：

其中，

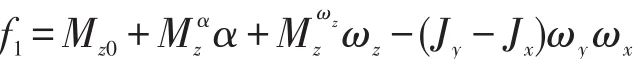
为了分析方便，假设弹体仅存在纵向运动［10］，有：

将式（2）中第一式代入式（1）中第二式，并经过等式两端求导，整理有：

再将式（4）中第一、二式代入式（1）中第二式，并经过等式两端求导，整理可得：

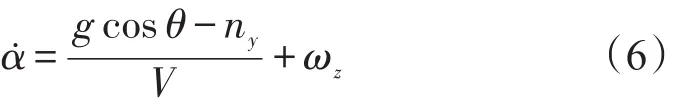
将式（6）代入式（5）得：

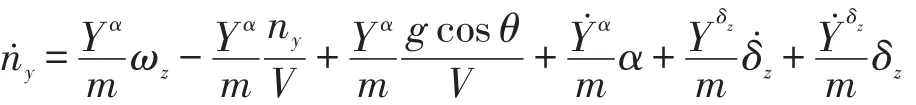
也可表达为：

其中，

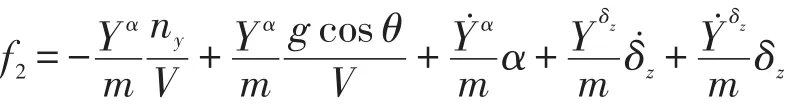
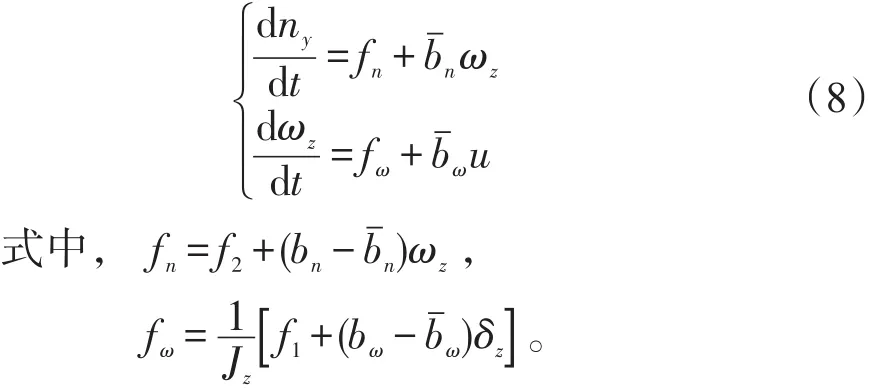
俯仰通道控制回路的设计，即以式（8）为系统模型，通过设计控制量u，使法向过载ny按要求跟踪指令过载。

系统控制的特性如下：

1）ny是被控量，ny和ωz均可由惯性仪表量测得到；

2）将fn和fω看作系统的未知扰动；

3）当未知扰动fn和fω能得到补偿时，u对ny完全能控。

2　俯仰通道自抗扰控制设计

2.1降阶LESO设计

考虑系统［11］：

式中，f（x,w,t）为系统的扰动，u（t）为控制量。构造降阶LESO［12］如下：

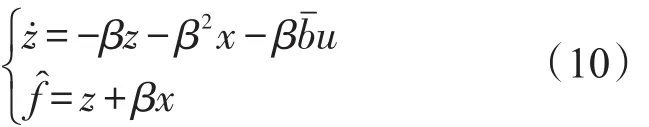
2.2ADRC控制

由于降阶LESO对系统扰动进行实时估计并予以动态补偿，便将式（9）的控制转化为对一阶积分环节的控制，再对u0设计控制律。

2.3俯仰通道ADRC控制设计

控制思想如下：

1）设ny_c为指令法向过载，由式（8）中第一式将ωz作为ny的控制量，将fn看作“干扰”。确定使ny跟踪ny_c的控制：

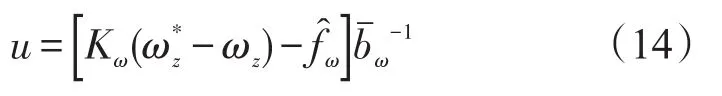
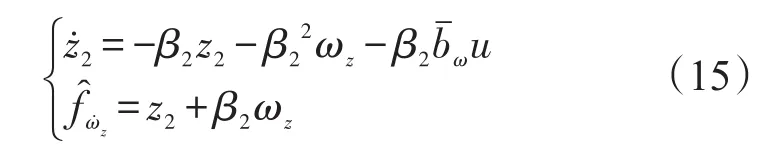
由式（12）～式（15）便构成了俯仰通道法向过载反馈控制。

ADRC控制回路设计如图1所示。

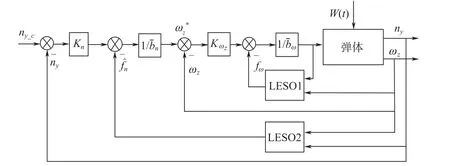
图1　控制系统框图Fig.1Block diagram of control system

整个控制回路的控制参数为（β1,β2,Kn,Kω）。两个LESO对系统扰动进行实时估计并予以动态补偿，控制参数确定简单，参数能够适应整个飞行包线。

3　试验验证

利用适合低速无人机使用的某小型制导炸弹，进行散态半实物仿真实验验证。以其典型弹道为例，仿真情况如下。

弹道条件：投放速度为70m/s，投放高度为5000m，射程为3500m。

约束条件：存在逆风20m/s；①理想模型，所用气动参数均由风洞试验得到；②偏差模型，对气动数据进行拉偏，特别地将增加40%。在实际系统中，控制模型均为偏差模型，系统设计与研制、飞行环境中诸多不确定因素均形成了系统扰动量。

ADRC控制参数选取为：

仿真结果如下。图2为采用理想模型下，PID 和ADRC对法向过载控制效果的比较。

图2理想模型下ADRC和PID仿真曲线Fig.2Simulation curves of the ADRC and PID in normal model

图3为采用偏差模型时，PID和ADRC对法向过载控制效果的比较。图4为ADRC控制中两个降阶LESO分别动态估计内部干扰的情况，其中系统被估计的干扰量中的噪声，是因为仿真中叠加了陀螺噪声形成的。

图3　偏差模型下ADRC和PID仿真曲线Fig.3Simulation curves of ADRC and PID in deviation model

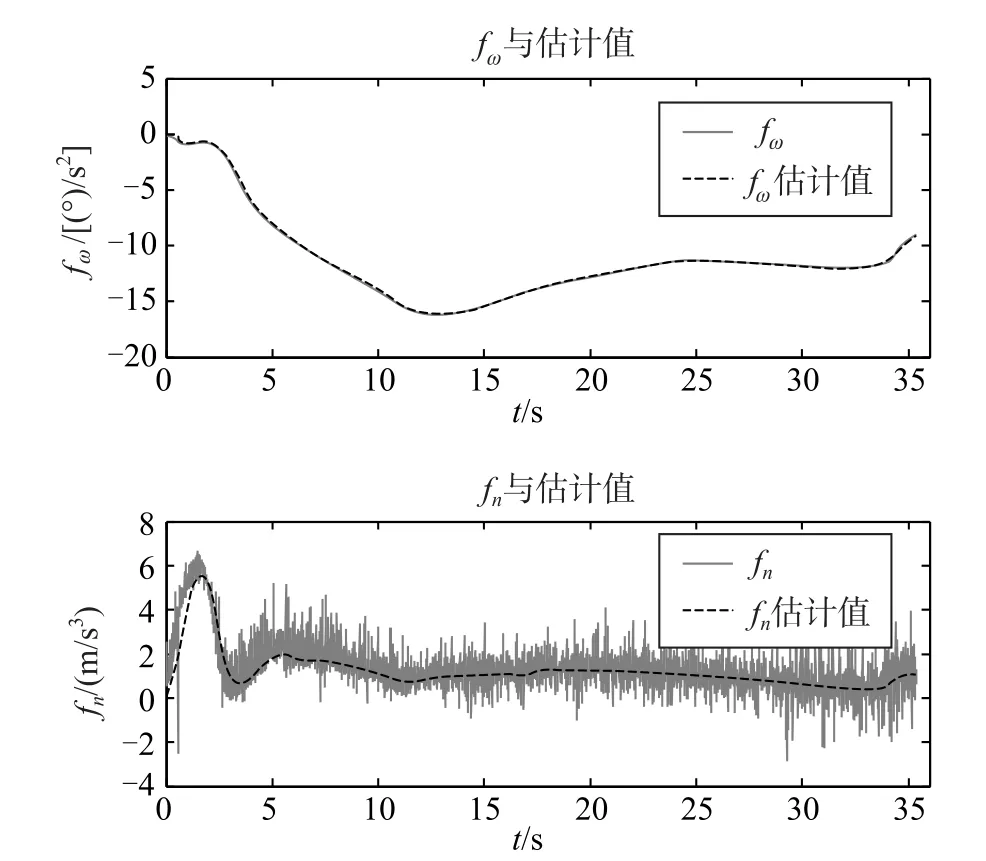
图4　降阶LESO对干扰的估计Fig.4Curves of estimating disturbance with reduceorder LESO

仿真表明，理想弹道情况下两种控制方案均具有较好的控制效果，但是，在飞行受到干扰情况下，二者控制效果存在较大差异，原用PID稳定控制品质变差；ADRC控制仍具有良好的控制效果，并且，通过两个降阶LESO输出曲线可知，ADRC实现了对干扰量的动态估计并实时补偿，具有较强的抗干扰能力和对环境较强的适应性。

大量仿真试验表明，在全飞行包线内，ADRC控制方法均能通过降阶LESO对系统扰动进行有效估计并予以动态补偿，控制品质较好。

4　结论

针对制导炸弹纵向通道控制，提出了自抗扰控制。该方法利用双降阶LESO对系统的总扰动进行实时估计并予以动态补偿，通过两个比例控制实现对俯仰通道法向过载的控制。仿真结果表明，该方法与原用PID控制相比较，控制品质优势明显，参数调节简单，抗干扰能力强。

［1］熊治国，董新民.程序调参飞行控制律的研究与展望［J］.飞行力学，2003，21（4）：9-l3. XIONG Zhi-guo，DONG Xin-min.Study and outlook of gain scheduling flight control law［J］.Flight Dynamics，2003，21（4）：9-13.

［2］Zhiqing Gao.Scaling and bandwidth-parameterization based controller turning［C］.Proceedings of American Control Conference，2003：4989-4996.

［3］Mingwei Sun，Zengqiang Chen，Zhuzhi Yuan.A practicalsolution to some problems in flight control［C］.Proceedings of 48thIEEE Conference on Decision and Control，2009：1482-1487.

［4］Wenchao Xue，Yi Huang.On frequency-domain analysis of ADRC for uncertain system［C］.Proceedings of American Control Conference，2013：6652-6657.

［5］Ruiguang Yang，Mingwei Sun，Zengqiang Chen.Active disturbance rejection control on first-order plant［J］. Journal of Engineering and Electronics，2011，22（1）：95-102.

［6］宋金来，金岳，杜志伟，等.扩张状态观测器在无人机纵向飞行控制中的应用［J］.飞行力学，2008，26（6）：76-78. SONG Jin-lai，JIN Yue，DU Zhi-wei，et al.Extended state observer used in UAV longitudinal flight control［J］. Flight Dynamics，2008，26（6）：76-78.

［7］宋金来，王晓燕，韩京清，等.卫星制导炸弹控制回路的自抗扰控制［J］.航天控制，2008，26（3）：25-29. SONG Jin-lai，WANG Xiao-yan，HAN Jing-qing，et al. Active disturbance rejection control of attitude control for GPS-guided bomb［J］.Aerospace Control，2008，26 （3）：25-29.

［8］李毅，陈增强，刘忠信.自抗扰技术在四旋翼飞行姿态控制中的应用［J］.哈尔滨工业大学学报，2014，46（3）：115-118. LI Yi，CHEN Zeng-qiang，LIU Zhong-xin.Attitude control of a quad-rotor robot based on ADRC［J］.Journal of Harbin Institute of Technology，2014，46（3）：115-118.

［9］陈新龙，杨涤，耿斌斌.自抗扰控制技术在某型导弹上的应用［J］.飞行力学，2006，24（1）：81-83. CHEN Xin-long，YANG Di，GENG Bin-bin.Application of auto-disturbance-rejection-controller to a missile［J］. Flight Dynamics，2006，24（1）：81-83.

［10］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京：北京理工大学出版社，2000. QIAN Xing-fang，LIN Rui-xiong，ZHAO Ya-nan.Missile flight dynamics［M］.Beijing：Beijing Institute of Technology Press，2000.

［11］韩京清.自抗扰控制技术［M］.北京：国防工业出版社，2008. HAN Jing-qing.Active disturbance rejection control technique［M］.Beijing：National Defense Industry Press，2008.

［12］薛文超.自抗扰控制的理论研究［D］.中国科学院研究生院，2012. XUE Wen-chao.On theoretical analysis of active disturbance rejection control［D］.University of Chinese academy of Science，2012.

Application ofActive Disturbance Rejection Control for Pitch Channel in Guided Bomb

ZHANG Yu-xiang，SONG Jin-lai，WANG Ming-guang，JIN Yue
（BeijingAerospace Institute of Microsystems，Beijing 100094）

This paper presents an active disturbance rejection control for overload control.Double linear extended states observers are proposed for on-line estimating and compensating the dynamics which lumps the internal dynamics and the external disturbance.The plant dynamics is reduced to a group of integrators with LESO，and proportion controller is used.The hardware-in-the-loop simulation results show the control system designed has more excellent character than PID controller.

PID；active disturbance rejection control（ADRC）；linear extended states observer（LESO）；overload control

U666.1

A

1674-5558（2016）01-01064

10.3969/j.issn.1674-5558.2016.01.003

张宇翔，男，硕士，研究方向为飞行器制导与控制。

2015-01-19