一种补偿惯性平台基座不水平的转位算法

孙超，倪娜，王汀，魏燕红

（北京航天控制仪器研究所，北京100039）



一种补偿惯性平台基座不水平的转位算法

孙超，倪娜，王汀，魏燕红

（北京航天控制仪器研究所，北京100039）

针对静基座平台系统调平进行了研究，详细分析了四轴平台系统台体坐标系、框架坐标系及基座坐标系间的空间关系，推导出了台体不同位置调平时框架角间的关系，设计了补偿平台基座不水平的转位方法。当基座不水平角度较大时，通过该方法可将平台直接转位至调平角度附近，不需经过粗调平便可直接进入精调平，从而可以使平台系统的工作过程得到简化，对于提高平台的任意位置转位及自标定、自瞄准效率有重要意义。

惯性平台系统；基座不水平；调平；平台转位

0　引言

惯性平台系统在测试过程中需经常进行台体任意位置转位，在进行自标定和自瞄准时也需将台体转位至特定位置。平台放置在试验台或安装在弹、箭上时，基座与地理水平面间一般存在小角度倾斜，当平台完成某位置调平工作后，台体与基座间存在偏差角。如进行锁零时，外环轴/随动轴/台体轴的角度可能为εx/0/εz（假设随动轴为方位轴，另外两轴为水平轴），εx、εz表示了基座在两个方向的不水平度。当基座不水平度较大时，平台进行调平后，台体与基座间的偏差角可达几度甚至十几度，在该情况下平台进行某些位置锁定时需要的粗调平时间较长，影响平台转位效率。考虑基座固定后台体在各位置的调平角度间存在确定的转换关系，通过该转换关系可由平台初始框架角计算出目标位置处框架角，以计算得到角度为目标框架角进行转位，转位过程中省略平台粗调平过程，使平台由粗转位直接进入精调平状态，从而可以简化平台系统的工作过程，对于提高平台的任意位置转位及自标定、自瞄准效率有重要意义。

1　四轴惯性平台

四轴平台是在原来的三轴平台的基础上，通过在最外面增加一个随动框架而构成的。原来的三轴平台的外框架轴通过轴承安装在随动框架轴上，而随动框架轴通过轴承安装在弹（箭）上。这样，平台共有4个自由度，因一般相对于惯性空间的稳定平台只需要3个自由度，因此就有1个多余的自由度，可以用来避免“框架锁定”现象。这种四轴平台在弹（箭）作大姿态角飞行时，里面的三个框架轴能始终保持相互垂直状态，因此称为全姿态稳定平台［1］，图1示出了这种平台的结构原理。

图1　平台系统框架结构图Fig.1The frame figure of platform system

为了实现弹体全姿态飞行以及避免在特定角度时平台丢失自由度，四轴平台系统随动环在实际工作中分为随动和随锁两个工作状态。随动状态时，随动框架跟随内框架运动，内框架与外框架固连，此时平台等效为由随动轴—外环轴—台体轴组成的三轴平台；随锁状态时，随动框架被锁定而与基座固连，此时平台等效为由外环轴—内转轴—台体轴组成的三轴平台。现分别推导平台随动框架在随动和随锁状态时各调平角度间的关系。

2　调平角度关系推导

当平台基座固定后，台体在不同姿态调平时的框架角间存在可推导的关系。设平台初始为锁零状态，基座坐标系、初始位置台体坐标系、目标位置台体坐标系关系如图2所示。图2中，βx、βz为平台锁零时外环轴和台体轴角度，该角度反映了基座的不水平程度；α、β、γ（克雷洛夫角）为目标位置处台体的空间姿态角；β'x、β'y、β'z为目标位置调平时各框架轴的角度。

图2　各坐标系间关系Fig.2The relationship between coordinate systems

2.1随动状态

随动状态时，图2中各坐标系间转换矩阵如下。

基座坐标系到锁零时台体坐标系的转换矩阵：

锁零时台体坐标系到目标位置台体坐标系转换矩阵：

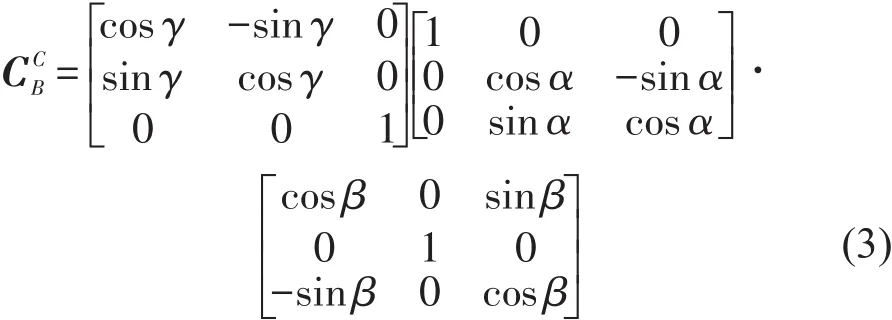
基座坐标系到目标位置台体坐标系转换矩阵：

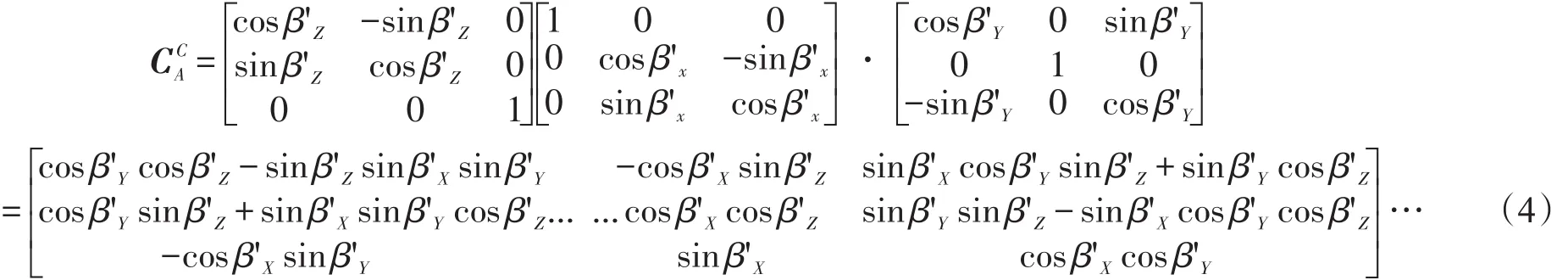
上述转换矩阵中βx、βz以及α、β、γ均为已知量，因此可根据式（1）、式（2）和式（3）求得转换矩阵为已知量，该矩阵与式（4）所求结果对应项相等，从而可求出目标位置台体调平时外环轴、随动轴、台体轴各轴的框架角β'x、β'y、β'z。

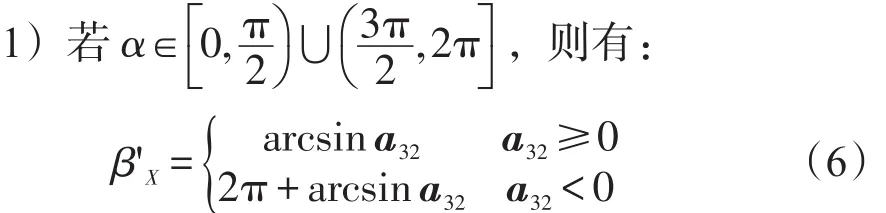
2.2随锁状态

锁零时台体坐标系到目标位置台体坐标系转换矩阵：

基座坐标系到目标位置台体坐标系转换矩阵：

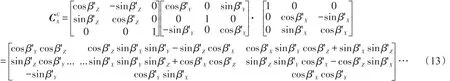
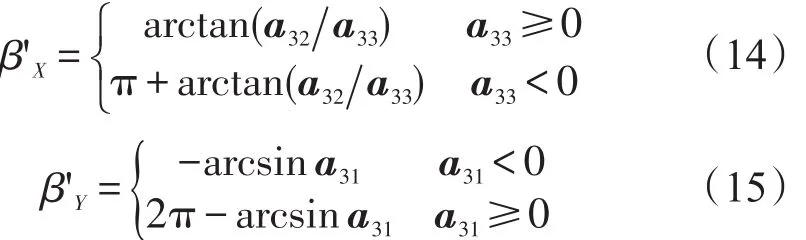
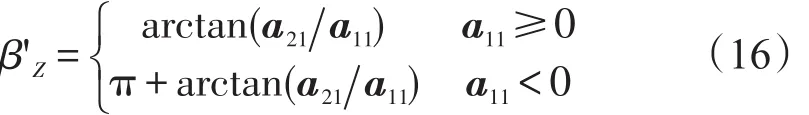
以上分别就随动框架在随动和随锁状态下，根据平台已知的初始位置（一般为锁零）时各框架轴的角度以及平台目标位置台体的空间姿态角，推算出了平台目标位置处调平后台体各框架轴的角度。

3　转位方法设计

根据第2节所推导的各角度间的关系，可实现平台静基座转位时对基座不水平的补偿。需要已知的条件是平台锁零时各框架轴的角度以及平台转位目标位置处的台体空间姿态角，根据上述已知角度推导出平台转位目标位置处各轴的框架角，然后以该框架角为输入角度进行快速转位，当偏差角为一小角度（如0.04°）时，切换为精调平和方位精确锁定，从而实现对平台基座不水平补偿的快速转位方法，具体转位流程如图3所示。

图3　平台转位过程Fig.3The process of platform rotation

4　实验验证

将以上所推导的结论及设计的转位方法在某型号惯性平台系统上进行实验验证。该型号惯性平台系统在调试过程中放置在具有隔离地基作用的大理石实验台上，大理石实验台的水平度优于1'，因此可认为平台工作在静基座条件下。

在实验过程中以随动轴作为方位轴，外环轴和台体轴作为水平轴，取两水平轴为锁零调平，方位轴分别为0°、60°、120°、180°、240°、300°共六个位置调平后的框架角进行验证。同时为使实验框架角不至于太小，在平台基座和大理石实验台间加入垫片以增加基座的不水平度，实验得到框架角的实际值和用本文推导方法得到的计算值如表1所示。

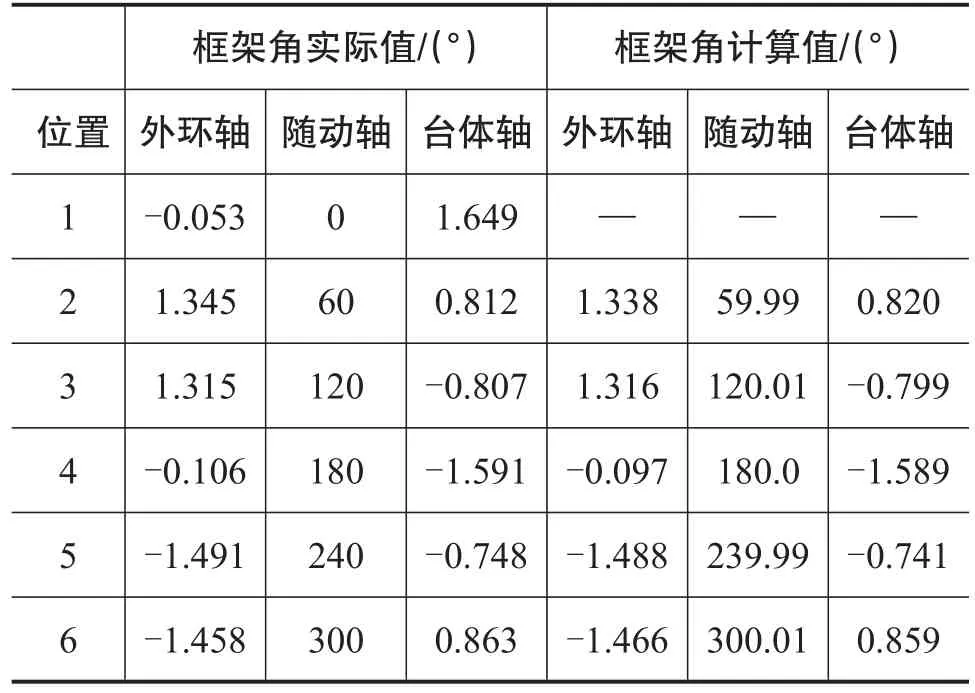
表1　实验过程中框架角的实际值和计算值Table 1The actual value and calculated value of gimbal angels in the test

从以上结果可以看出，用本文方法计算得到的框架角的值与平台实际调平后框架角的偏差在±0.01°以内，该角度满足平台切换为精调平时的偏差角要求（±0.04°）。因此将所设计转位方法在平台上进行验证，实验同样取两水平轴为锁零调平，方位轴分别为0°、60°、120°、180°、240°、300°共六个位置，实验得到平台转位和调平锁定过程中各框架轴角度如图4所示。

图4　平台转位实验结果Fig.4The experiment result of platform rotation

从图4中可以看出，平台可实现由粗转位直接切换为精调平，并最终完成调平。实验中方位轴有5次转位过程，每次转位过程中平台切换为精加矩时，两水平轴的初始角度和平台调平稳定后两水平轴的最终角度如表2所示。从表2可知，平台进入精调平后水平轴的初始角度与最终角度间的偏差Δ均在±0.04°以内，说明本节所设计的转位方法是正确有效的，相对于原有转位方法省略了粗调平过程，减小了平台切为精调平时的初始偏差角，缩短了平台精确锁定所需时间。

表2　调平过程中框架角的初始值和最终值Table 2The initial value and final value of gimbal angels in the leveling

5　结论

本文通过对平台在不同姿态角时台体、基座间的空间相对位置进行分析，推导出了台体在不同位置调平后框架角之间的关系。在此基础上设计了一种补偿静基座惯性平台系统基座不水平的转位方法，通过实验验证了该方法的正确性及可行性。从而可实现平台转位时省略粗调平，减小切为精调平时的偏差角，优化平台的调平过程，在一定程度上减少平台调平所用时间，对于提高平台的任意位置转位、自标定、自瞄准效率有重要意义。

［1］陆元九.惯性器件［M］.北京：中国宇航出版社，1990. LU Yuan-jiu.Inertial device［M］.Beijing：China Aerospace Press，1990.

［2］秦永元.惯性导航［M］.北京：科学出版社，2006. QIN Yong-yuan.Inertial navigation［M］.Beijing：Science Press，2006.

［3］邓益元.静压液浮陀螺平台系统［M］.北京：中国宇航出版社，2012. DENG Yi-yuan.Hydrostatic liquid-bearing gyro stabilized platform［M］.Beijing：ChinaAerospace Press，2012.

［4］胡寿松.自动控制原理［M］.北京：科学出版社，2007. HU Shou-song.Automatic control theory［M］.Beijing：Science Press，2007.

［5］武清玺，冯奇.理论力学［M］.北京：高等教育出版社，2003. WU Qing-xi，FENG Qi.Theoretical mechanics［M］.Beijing：Higher Education Press，2003.

ARotation Method for Compensating the Foundation Inclination of Inertial Platform

SUN Chao，NI Na，WANG Ting，WEI Yan-hong
（Beijing Institute ofAerospace Control Devices，Beijing 100039）

This paper calculates the gimbal angle relationships when the body leveling at different positions through analyzing the coordinate transformation between platform，frame and foundation of the four-axis platform，puts a rotation method for compensating the foundation inclination of inertial platform.Using the method can omit coarse calibration and switch delicate leveling directly during platform rotating.So it can predigest the work process of inertial platform system and make sense of improving the efficiency of self-calibration，self-alignment and platform rotation.

PINS；foundation inclination；adjusting level；platform rotating

U666.1

A

1674-5558（2016）01-01029

10.3969/j.issn.1674-5558.2016.01.005

孙超，男，硕士，研究方向为导航、制导与控制。

2014-12-08