一种基于磁盘内和磁盘间冗余的混合编码方案
2016-10-13卞建超查雅行罗守山
卞建超 查雅行 罗守山 李 伟
(北京邮电大学计算机学院 北京 100876)(灾备技术国家工程实验室(北京邮电大学) 北京 100876)
一种基于磁盘内和磁盘间冗余的混合编码方案
卞建超查雅行罗守山李伟
(北京邮电大学计算机学院北京100876)(灾备技术国家工程实验室(北京邮电大学)北京100876)
(bianjianchao@bupt.edu.cn)
云计算的发展和应用对存储系统的容错能力提出了更高要求.纠删码被广泛运用于计算磁盘级冗余以抵抗磁盘错误,但抵抗扇区错误时磁盘利用率较低,现有针对扇区错误的优化方案只能抵抗较小数目或者特定分布的扇区错误.为此,利用MDS(maximum distance separable)码的同态性质,提出了一种将磁盘间冗余与磁盘内冗余相结合的混合编码(intra- and inter-device redundancy, IIDR).添加校验磁盘抵抗磁盘错误的同时,在数据磁盘中添加全局校验扇区以抵抗扇区错误,利用磁盘内编码添加本地校验扇区,以优化处理单个扇区错误的性能.最后,正确性证明及性能分析的结果表明所提方案能抵抗磁盘错误和任意分布的扇区错误,并且恢复单个扇区错误计算开销低,更新性能较好,同时与传统的磁盘内编码方案相比,有较高的磁盘利用率.
云计算;磁盘错误;潜在扇区错误;纠删码;磁盘内冗余
随着云计算相关技术的发展,各大厂商也陆续推出了商用的云服务,用户量的激增、业务模式的扩展、服务保障要求的提高,都对数据的可用性提出了更高要求,现有数据容错机制的改进加强迫在眉睫.造成数据丢失的设备故障可以分为磁盘错误(device failures)和扇区错误(sector failures)[1],磁盘错误会导致出错磁盘上的数据全部丢失,扇区错误则会导致单个扇区上的数据不可用.造成设备故障的因素有很多,介质材料不合格、松动微粒引起的介质划痕、高飞写入(high fly writes)造成的异常位模式、振动、磁头触及介质、偏离磁道的读写都有可能造成设备故障[2].随着使用垂直记录技术的几千兆级磁盘打入市场,其更高的磁录密度、更窄的磁道宽度、更贴近磁盘的浮动磁头,也更容易被软颗粒污染物划伤[2].此外,随着固态硬盘(solid state drive, SSD)生产成本降低,大规模应用成为可能,但与机械硬盘(hard disk drive, HDD)不同的是,SSD的单个扇区错误发生的概率是随着写操作的次数增长而增大的[3].
相对于设备错误,潜在扇区错误(latent sector errors, LSEs)在读取该扇区的数据之前无法检测,这种类型故障对数据的可用性造成了很大风险.当设备错误出现后,需要使用独立冗余磁盘阵列(redundant arrays of independent disks, RAID)重建数据,但此时有磁盘出现LSEs就有可能造成数据重建失败[4].
1 相关工作
针对扇区错误开展的研究有很多,目前主要有2种解决方案:1)scrubbing方案[5],该方案是周期性地在后台对各磁盘进行扫描,发现LSEs后使用RAID冗余对其进行修复,该方案已经在NetApp的系统上部署商用了;2)IDR(intra-disk redundancy)方案,该方案在每个磁盘内添加校验冗余,并配合具有磁盘间冗余的RAID一起应用.一些文件系统[6]在磁盘中对部分元数据进行备份,IRON(internal robustness)文件系统[7]对每个文件添加校验单元.Dholakia等人[8]提出了对1个磁盘中所有数据块添加校验冗余的方案,其实就是纠删码在单个磁盘内的应用,但以上方案都需要与磁盘间容错的RAID搭配应用.Iliadis等人[9]对比分析了scrubbing方案与IDR方案,指出scrubbing方案在数据量极为庞大的今天,周期地扫描每块磁盘的做法显然效率低下.然而,IDR方案在每个磁盘添加冗余的方法,其磁盘利用率也很低.特别是在同时出现磁盘错误和LSEs的混合错误模式下,以上方案都无法独立解决,但传统的纠删码为了容忍额外的扇区错误需要添加整块的冗余磁盘,容错效率同样低下.
针对混合错误模式,2013年 Plank等人[10-11]提出了SD Codes,该方案在校验磁盘的基础上添加全局校验扇区对抗扇区错误,如在添加1块校验磁盘和2个全局校验扇区的情况下,SD Codes是介于RAID5与RAID6之间的解决方案.相对于传统纠删码,该方案能够容忍1个磁盘错误、2个扇区错误,而不用添加第2块冗余校验磁盘.相对于IDR方案在每块磁盘上添加同等数量的校验扇区,该方案在磁盘利用率上有很大优势.但该方案最多只能容忍每个条带3个扇区错误,而且还有其他参数限制.
2014年Li等人[1,12]提出了STAIR Codes方案,该方案提出了一种更一般化的应对混合错误模式的编码方法,使用向量e表示扇区错误分布,在数据磁盘上添加相应分布的全局校验扇区以抵抗扇区错误.该方案需要2种MDS(maximum distance separable)码分别承担行编码和列编码,相比于SD Codes,该方案能够容忍更多扇区错误,并能灵活套用任意系统MDS码,相比于传统的IDR方案,STAIR Codes有更高的磁盘利用率.但STAIR Codes需要向量来表示错误分布情况,即STAIR Codes只能容忍特定分布的s个扇区错误,在实际部署时有一定局限性.Schroeder等人[4]的扇区错误分析指出,不同类型的磁盘90%~98%的扇区错误是单独出现,即存储系统面临的风险绝大多数来自孤立的扇区错误.但在处理单个扇区错误时,STAIR Codes仍需读取多个磁盘以恢复数据,IO及计算开销比传统IDR方案大.
针对现有方案的缺陷,本文提出了一种基于磁盘内和磁盘间冗余的混合编码算法(intra- and inter-device redundancy, IIDR)方案.本方案结合了磁盘内编码在修复小规模扇区错误时IO、计算开销上的优势,又解决了其对抗大规模扇区错误时磁盘利用率急剧下降的缺点.相对于STAIR Codes方案,本方案牺牲了一定的磁盘利用率,解决了其不能抵抗任意扇区错误的问题,并优化了在应对小规模特别是单个扇区错误时的IO及计算性能.
2 混合编码方案
本节首先给出预备知识及基本定义,然后分别介绍本方案编码及数据恢复过程.
2.1预备知识
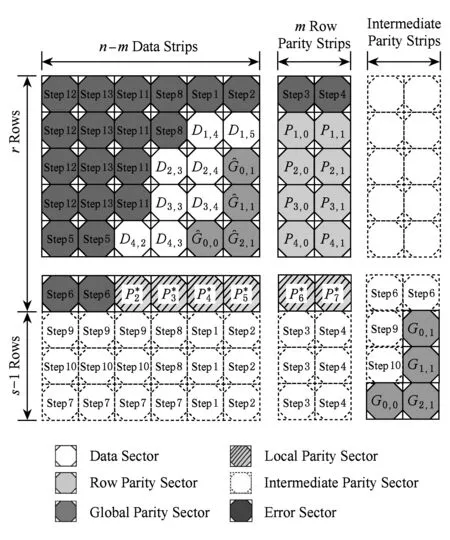
一个由n块磁盘组成的存储系统,包括一定数量的数据磁盘和校验磁盘,其中校验磁盘所存数据由数据磁盘编码计算而来,与同一次编码计算相关的所有数据称为条带(stripe),存储系统也可以看作为多个条带的组合.同一磁盘上同属一个条带的数据集合称为条块(stripchunk),条块又由若干扇区(sectorelementsymbolblock)组成,个数记为r,扇区为编码基本计算单元[13].如图1所示,条块由r个扇区组成,条带由n个条块组成,条带可以看成由扇区组成的r×n矩阵.

Fig. 1 Relationship between sector, strip and stripe.图1 扇区、条块、条带三者关系
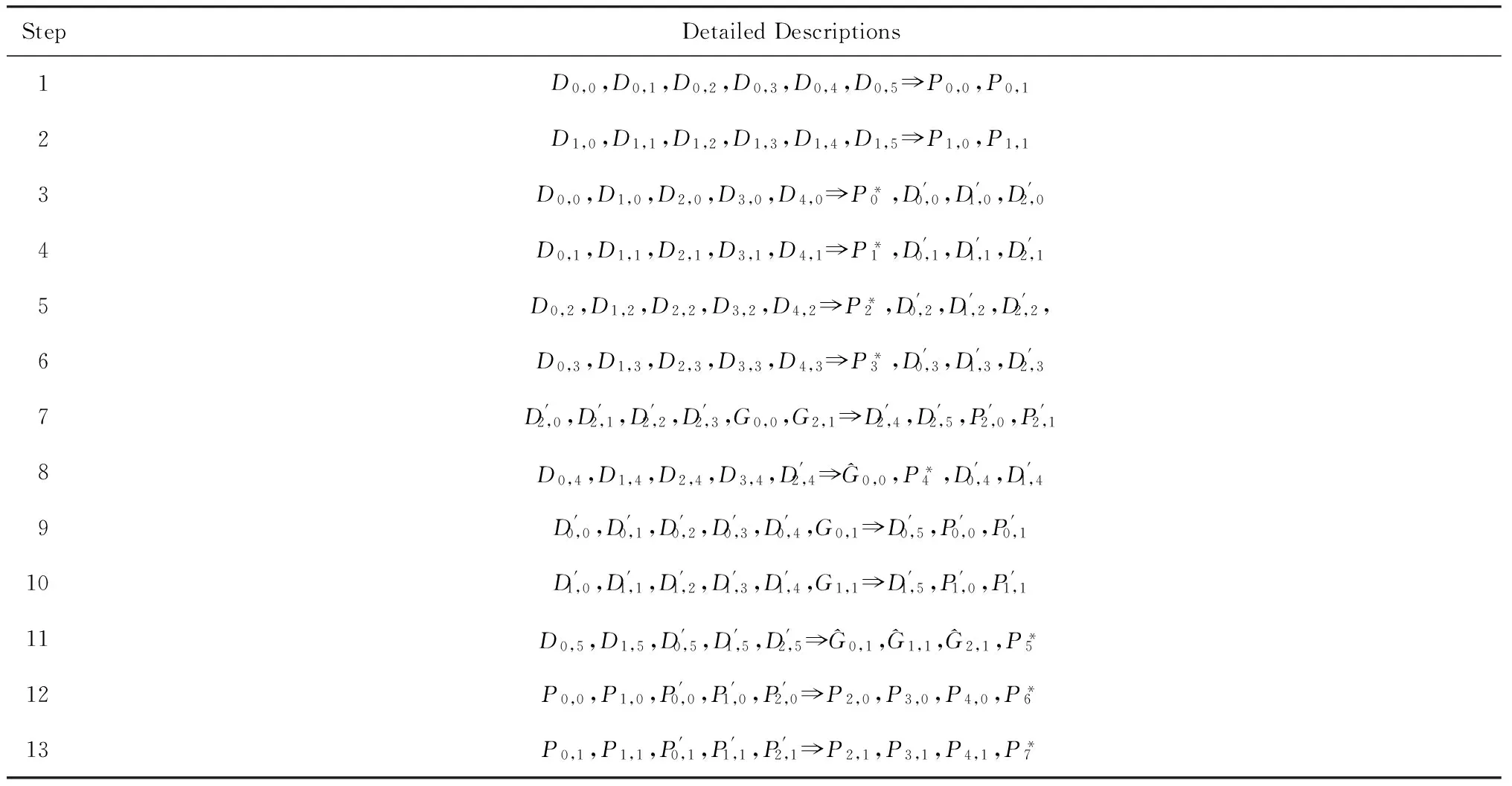
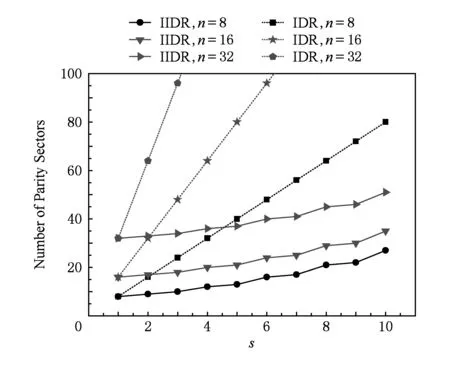
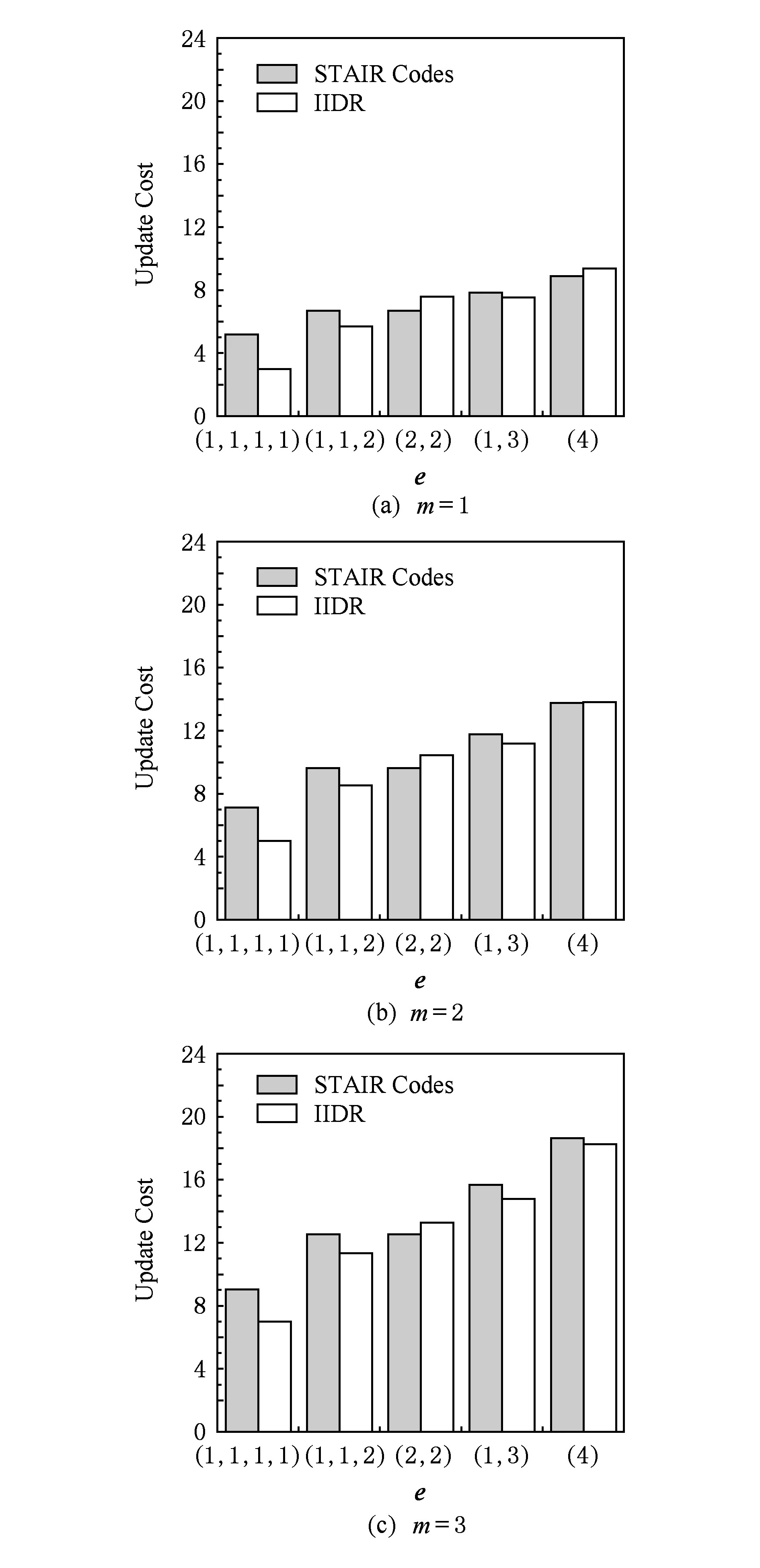
如上所述,各条带在编码时相互独立,可以以条带为单位来进行讨论.存储系统面临的威胁有磁盘错误和扇区错误,可以把磁盘错误映射为条带中的条块错误,即整个条块数据丢失或损坏.本文提出的方案能抵抗条带中同时出现m(m 2.1.1校验扇区分布 本方案的目标是能抵抗s个扇区错误,需添加相同分布的校验扇区(证明见第3节),而s个扇区错误的分布有很多种可能,所以添加的校验扇区应覆盖其所有可能分布.如s=4时,可能的分布就有(4),(3,1),(2,2),(1,1,1,1),添加的校验扇区分布应为(4,2,1,1).若要抵抗s个扇区错误,需添加的校验扇区的分布为 (证明见第3节).为了优化单个扇区错误恢复性能,本方案在每个条块中添加一个本地校验扇区,所以本方案校验扇区分布为 则全局校验扇区分布实际为 本方案总计校验扇区个数为s′+n. 2.1.2基本定义 本方案涉及使用2种系统MDS码,一种为磁盘间编码(行编码),采用(n+m′,n-m)码作为行编码算法,记为Crow;另一种为磁盘内编码(列编码),采用(r+s-1,r-1)码作为列编码算法,记为Ccol.所以将本方案命名为磁盘内和磁盘间冗余编码. 2.1.3同态性质 根据定义,各列进行编码计算有: 当0≤j≤n-m-1时, 当0≤k≤m-1时, 当0≤t≤s-2时, 2.2编码过程 2.2.1示例 首先通过实例来介绍本方案编码过程,图2中取值n=8,m=2,r=6,s=4,即有6个数据条块、2个校验条块,每个条带添加分布为(3,1)的全局校验扇区,此外每个条块添加1个扇区作为本地校验扇区.行编码、列编码分别需采用(10,6)码、(9,5)码.具体步骤如表1所述,本方案编码思想是利用MDS码的同态性质,配合置0的外部全局校验扇区完成编码计算. Fig. 2 Encoding algorithm.图2 编码算法 2.2.2一般情况 Table 1 Detailed Steps for Encoding 根据全局校验扇区的分布,本方案编码由以下4步组成: 1) 计算0至n-m-m′-1列各校验扇区 根据定义,计算条带中0至r-s-1行、0至n-m-m′-1列不包含全局校验扇区.此类行和列可以直接进行编码计算: ① 计算行校验扇区(不包含全局校验扇区的行), 其中0≤i≤r-s-1; ② 计算本地校验扇区及相应的临时列数据扇区(不包含全局校验扇区的列), 其中0≤j≤n-m-m′-1. 2) 计算n-m-m′至n-m-2列各校验扇区 算法1. 编码循环算法. 初始化: Rr;*行中数据完好的扇区数目* Rc;*列中数据完好的扇区数目* Sett=2,i=0,q=0,j=0,p=0. t=t+i; 搜索第r+s-t行; 记录Rr; IfRr=n-mThen 对r+s-t行进行编码; Else break; End If Forj=qtom′-2 搜索第n-m-m′+i列; 记录Rc; IfRc=r-1 Then 对n-m-m′+i列进行编码; p=p+1; Else break; End If End For q=j+p; p=0; End For 输出:从n-m-m′到n-m-2列. 3) 计算n-m-1列各校验扇区 经过第2步运算,r至r+s-m′-1行都存在n-m个已知扇区,可调用行编码算法进行计算, 其中0≤t≤s-m′-1; 全局校验扇区全部计算完毕. 4) 计算n-m至n-1列(磁盘校验条块)剩余扇区 其中0≤k≤m-1. 至此,条带中的校验扇区全部计算完毕. 2.3数据恢复过程 2.3.1示例 图3为本方案数据恢复示例,其中取值n=8,m=2,r=6,s=4,图3中黑色表示出错扇区,即出现2个条块错误及分布为(4,2,1,1,1,1)的扇区错误,即该参数下本方案能抵抗最严重错误情况,通过这个示例来阐述本方案数据恢复算法,具体操作如表2所示. Fig. 3 Data recovery algorithm.图3 数据恢复算法 本方案数据恢复思路是先使用本地校验扇区修复单个扇区错误,再结合置0的外部全局校验扇区计算出部分临时行扇区,使得部分列达到列编码条件并恢复,依次类推直到数据完全恢复. Table 2 Detailed Steps for Data Recovery 2.3.2一般情况 本方案为了能抵抗s个任意分布的扇区错误,添加了大于s的校验扇区,实际容错上限为校验扇区相同分布的扇区错误(证明见第3节),即出现m个条块错误和分布为的扇区错误. 1) 修复简单错误 列内只存在单个扇区错误或者行内扇区错误数为m的情况,即恢复数据只涉及1次解码计算,称为简单错误.首先处理列内只存在单个扇区错误的情况,很显然此类列存在r-1个完好扇区,可调用列编码算法Ccol(r+s-1,r-1)恢复数据,如表2的Step1~4;接着处理扇区错误数为m的行,可知该行完好扇区个数为n-m,可调用行编码算法Crow(n+m′,n-m)恢复数据,如表2中的Step5~6. 2) 修复连续扇区错误 ① 修复m+1至m+m′-1 列 ② 修复第m列(s个扇区错误) 此时,r至r+s-m′-1行都存在n-m个已知扇区,可调用行编码算法进行计算, 其中0≤t≤s-m′-1. 使得第m列拥有r-1个已知扇区,可调用列编码算法Ccol(r+s-1,r-1)恢复该列剩余扇区, 3) 修复0至m-1列(条块错误) 经过步骤1,条块错误所在列仍有s个扇区错误,经过步骤2计算此类列存在r-1个已知扇区,可调用列编码算法恢复所有扇区错误: 其中0≤j≤m-1. 至此,全部数据均被修复. 上述算法为本方案能够容忍的最严重错误情况,很显然针对一般错误情况(m个磁盘错误,任意分布的s个扇区错误)本方案仍能胜任,具体正确性证明会在第3节进行阐述. 引理1.s个扇区错误所有分布的叠加为 证明. 设s个扇区错误分布为(e0,e1,…,em′-1),其中1≤m′≤s,且有e0+e1+…+em′-1=s,为便于讨论设e0≥e1≥…≥em′-1.按照m′不同的取值来进行讨论验证: 1)m′=1,即s个扇区错误分布在同一磁盘,e0=s; 2)m′=2,则分布为(e0,e1),可知e0+e1=s且e0≥e1,则当e0=e1=s2时e1取值最大,由于e0,e1为整数且e0≥e1,则e1的取值上限为s; 3)m′=3,则分布为(e0,e1,e2),可知e0+e1+e2=s且e0≥e1≥e2,则当e0=e1=e2=s3时e3取值最大,由于e0,e1,e2为整数且e0≥e1≥e2,则e2的取值上限为s. 证毕. 引理2. 本方案能抵抗与校验扇区相同分布的扇区错误. 根据命题,此时存在同样分布的扇区错误,其中单个扇区错误可以用本地校验扇区独立恢复,剩余需要恢复分布为(λ0+1,λ1+1,…,λm′-1+1)的错误扇区.可知此时计算条带中每行都存在n-m-m′个可用扇区,最后λ0行都存在m′个外部全局校验扇区(置0),满足行编码条件,调用Crow恢复最后λ0行的剩余扇区(临时列校验扇区).λ0+1个错误扇区所在列存在r-1个可用扇区(r-λ0-1个数据扇区、λ0个临时列校验扇区),满足列编码条件,调用Ccol能够恢复该列λ0+1个错误扇区. 此时,剩余行存在n-m-m′+1个可用扇区,配合λ1-λ0行都存在m′-1个外部全局校验扇区,满足行编码条件,调用Crow恢复λ1-λ0行所有扇区.计算后λ1+1个错误扇区所在列满足列编码条件,能够恢复该列λ1+1个错误扇区. 恢复完λi-1(1≤i≤m′-1)个错误扇区所在列后,配合λi-λi-1行都存在m′-i个外部全局校验扇区,可以调用Crow计算λi-λi-1行所有扇区,由此可以调用Ccol恢复λi+1个扇区错误所在列的所有数据.依次循环计算可以将全部错误扇区恢复. 因此,本方案能抵抗与校验扇区相同分布的扇区错误. 证毕. 定理1. 本方案若添加分布为 的校验扇区,则能抵抗s个任意分布的扇区错误. 证明. 根据引理2,若想抵抗s个扇区错误,需添加相同分布的s个校验扇区.根据引理1可知s个扇区错误所有分布的叠加为 很显然分布本方案添加的校验扇区包含该值. 因此,本方案若添加分布为 的校验扇区,则能抵抗s个任意分布的扇区错误. 证毕. 如第1节所述,本文提出了一种基本磁盘间和磁盘内冗余的混合编码算法(IIDR).本节从磁盘利用率、计算开销、更新性能3个方面,通过与经典的磁盘内冗余方案IDR及混合编码方案SD Codes,STAIR Codes做对比,来分析本方案各方面性能的优劣. 4.1磁盘利用率 随着数据爆炸性的增长,磁盘利用率成为衡量编码算法优劣的重要指标.由于STAIR Codes,IDR及本方案在同等容错能力下校验磁盘数目一致,所以数据磁盘中校验扇区的多少决定了一个方案磁盘利用率的高低,所需校验扇区越多则磁盘利用率越低.图4中取值n=8,r=6,分别计算了抵抗4个扇区错误的5种分布情况下各方案单个条带的校验扇区数目. 如图4所示,抵抗特定分布的扇区错误,STAIR Codes只需添加对应分布的校验扇区,即只需4个校验扇区,该方案所需添加的校验扇区最少;本方案除了添加全局校验扇区,还在每个条块中都添加了本地校验扇区,所以本方案校验扇区数略大于STAIR Codes方案;IDR方案需要在每个条块添加最大错误数的本地校验扇区,即校验扇区数目为最大错误数与n之积,所以随着最大错误数的增大,IDR方案变化十分明显.可以看出在抵抗特定分布扇区错误时,本方案磁盘利用率介于STAIR Codes与IDR方案之间. Fig. 4 The number of parity sectors for different e.图4 校验扇区数目 由于STAIR Codes方案不支持任意扇区错误分布,只能对比IDR方案与本方案在面对任意错误分布时的磁盘利用率.本方案添加的校验扇区分布为 则数目可以表示为 图5中分别取值n=8,16,32,分析对比2种方案在s不同的取值下校验扇区数量的变化. Fig. 5 The number of parity sectors for different s.图5 s不同取值下校验扇区数目 如图5所示,同一n取值下,2方案所需校验扇区数量与s成正比,IDR方案所需校验扇区更多,且增长速率也大于本方案.由于2个方案都是在每个磁盘上添加校验扇区,在同一s取值下,2方案所需校验扇区数量与n成正比,同样IDR方案所需校验扇区多于本方案,且增长速率大于本方案.综上所述,在抵抗任意错误分布的情况下,本方案的磁盘利用率优于IDR方案. 4.2计算开销 为了量化分析编解码算法的计算开销,将算法分解成若干步基本操作Mult_XORs[14],以步骤的多少来衡量一个算法计算开销的大小 ,很显然分解的操作越少,则计算开销较小.基本操作Mult_XORs(R1,R2,α)定义为若干字节数据R1与常量α相乘,所得的值与R2异或求和.如:(n,k)码的编码过程可以分解成k×(n-k)步基本操作. 4.2.1修复混合错误的计算开销 本方案在编解码过程中,共调用了n次纵向编码算法Ccol(r+s-1,r-1),计算产生了n个本地校验扇区、s′个全局校验扇区、(n-m)×(s-1)-s′个临时校验扇区、m×(s-1)个行校验扇区.调用r-1次横向编码算法Crow(n+m′,n-m),计算产生了m×(r-s)个行校验扇区、m×(s-1)+s′个临时校验扇区.分解成基本操作Mult_XORs,步骤数β为 图6为s=4时5中不同错误分布情况下本方案与STAIR Codes方案计算开销对比,其中n=8,m=2,r=8,16,24.如图6所示,本方案总体性能与STAIR-Upstairs算法相近,由于本方案添加了本地校验扇区,在修复单个扇区错误时不需要调用全局校验扇区,只需进行1次解码运算,所以在抵抗单个扇区错误较多的分布时,本方案β值略小于STAIR-Upstairs算法. 图7为s,n,r不同取值时β的变化情况.如图7所示,β与s成正比,且随着n,r的取值增大,β的增长速率变大.可以看出抵抗s个扇区错误,编码条带的规模也影响了计算性能,规模越大,开销越大. 4.2.2恢复单个扇区错误的计算开销 假设条带中出现m个条块错误(对应磁盘错误)及单个扇区错误,对比分析STAIR Codes方案的Upstairs,Downstairs两种算法与本方案恢复错误数据的计算开销.各方案恢复条块错误的操作基本一致,不同之处在于恢复单个扇区错误.本方案只需要扇区错误所在条块调用1次列编码算法即可完成扇区数据恢复,总计操作数为 Fig. 6 The number of Mult_XORs of STAIR Codes,IIDR versus different e.图6 抵抗不同分布错误时STAIR Codes,IIDR方案Mult_XORs操作数 Fig. 7 The number of Mult_XORs of IIDR.图7 IIDR方案Mult_XORs操作数变化图 而STAIR Codes方案的Upstairs,Downstairs两种算法都需要结合外部全局校验扇区来恢复扇区数据,总计操作数分别为 从公式上来看,本方案计算开销小于其他2种算法.图8是n,r取不同值时本方案与STAIR Codes方案3种算法恢复计算操作数对比. Fig. 8 Compute overhead of a single sector error recovery.图8 单个扇区错误恢复计算开销 如图8所示,由于本方案添加了本地磁盘校验,修复单个扇区错误时只需在本地进行1次解码操作,所以在不同的取值组合下本方案操作数均小于其他2种算法,特别是随着n,r取值增大时,STAIR Codes行、列编码矩阵增大,计算复杂度进一步增大,本方案优势更加明显.综上所述,本方案在抵抗单个扇区错误时计算开销小于STAIR Codes方案. 再考虑只发生单个扇区错误的情形,本方案仍通过磁盘内冗余进行修复,只需接入读取1块磁盘;而STAIR Codes则需要利用磁盘间冗余修复,需要读取n-m块磁盘.此种情形下,本方案IO性能也优于STAIR Codes方案. Fig. 9 Update cost of SD Codes, IDR, IIDR for different s.图9 s不同取值下SD Codes,IDR,IIDR的更新开销 4.3更新性能 当数据扇区更新时,相应的校验扇区也需要更新,可以通过所需更新的校验扇区数目来衡量方案的更新性能.更新开销定义为在1个条带中更新1个数据扇区时,所需更新的校验扇区数目的平均值. Fig. 10 Update cost of STAIR Codes, IIDR versus different e.图10 抵抗不同分布错误时STAIR Codes,IIDR方案更新开销 图9为n=8,r=6,s,m不同的取值情况下,SD Codes,IDR,IIDR三个方案更新开销的对比.如图9所示,3个方案中,SD Codes方案所需更新的全局校验扇区仅为s,行校验扇区仅为m,所以SD Codes方案有较好的更新性能.当s较小时,3个方案相差不大;当s较大时,本方案全局校验扇区数目增大,IDR方案则需要更新较多的行校验扇区,所以SD Codes方案优势更为明显,但SD Codes方案只能抵抗s≤3的任意错误分布.本方案开销整体略高于IDR方案,2个方案所需更新的行校验扇区基本一致,但随着s,m的增大,IDR需要更新更多的本地校验扇区,则本方案与IDR方案更新开销差距随即缩小. 由于STAIR Codes方案不支持任意错误分布,只能在抵抗特定错误分布的情况下分析其更新性能.图10中设s=4,针对其5种分布及m的不同取值,分析对比STAIR Codes与本方案的更新性能.如图10所示,2个方案性能相差不大,在不同分布下各有优劣.其中分布为(2,2),(4)的情况下,STAIR Codes更新性能较优;分布为(1,1,1,1),(1,1,2),(1,3)的情况下,本方案更新性能较优.这是由于2个方案所需更新的磁盘校验扇区数目基本一致,更新差距主要集中在全局校验扇区,由于本方案校验扇区由本地校验扇区和全局校验扇区组成,其中全局校验扇区数目比STAIR Codes少,更新时本方案只需更新单个本地校验扇区及全局校验扇区,所以更新开销比STAIR Codes小,特别是在单个扇区错误较多的分布,这种优势尤为明显. 综上所述,本方案更新性能总体优于STAIR Codes方案,特别是在抵抗存在单个扇区错误分布情况下优势较为明显.在抵抗任意扇区错误分布时,SD Codes方案更新性能最优(s≤3),本方案总体略差于IDR方案,但在部分参数下本方案优于IDR方案. 本文将磁盘间编码与磁盘内编码相结合,提出一种能抵抗磁盘错误和任意分布的扇区错误的混合编码方案.与传统的IDR方案相比,本方案有更高的磁盘利用率;相比SD Codes方案,本方案能够抵抗更多任意分布的扇区错误;相比STAIR Codes方案,本方案牺牲了一定的磁盘利用率,但能抵抗任意分布的扇区错误,更新性能也略优,特别是在处理单个扇区错误时有更小的IO和计算开销. [1]Li M, Lee P P C. STAIR codes: A general family of erasure codes for tolerating device and sector failures[J]. ACM Trans on Storage, 2014, 10(4): 1-30[2]Bairavasundaram L N, Goodson G R, Pasupathy S, et al. An analysis of latent sector errors in disk drives[C]Proc of the 2007 ACM SIGMETRICS Int Conf on Measurement and Modeling of Computer Systems. New York: ACM, 2007: 289-300[3]Micron Technology, Inc. N-29-17: NAND flash design and use considerations introduction Micron[EBOL]. 2006 [2015-06-01]. https:www.micron.com~mediadocumentsproductstechnical-notenand-flashtn2917.pdf[4]Schroeder B, Damouras S, Gill P. Understanding latent sector errors and how to protect against them[J]. ACM Trans on storage, 2010, 6(3): 523-530[5]Oprea A, Juels A. A clean-slate look at disk scrubbing[C]Proc of the 8th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2010: 57-70[6]McKusick M K, Joy W N, Leffler S J, et al. A fast file system for UNIX[J]. ACM Trans on Computer Systems, 1984, 2(3): 181-197[7]Vijayan P, Lakshmi N B, Nitin A, et al. IRON file systems[C]Proc of the 20th ACM Symp on Operating Systems Principles. New York: ACM, 2005: 206-220[8]Dholakia A, Eleftheriou E, Hu X Y, et al. A new intra-disk redundancy scheme for high-reliability RAID storage systems in the presence of unrecoverable errors[J]. ACM Trans on Storage, 2008, 4(1): 133-169[9]Iliadis I, Haas R, Hu X Y, et al. Disk scrubbing versus intra-disk redundancy for high-reliability raid storage systems[C]Proc of the 2008 ACM SIGMETRICS Int Conf on Measurement and Modeling of Computer Systems. New York: ACM, 2008: 241-252[10]Plank J S, Blaum M. Sector-disk (SD) erasure codes for mixed failure modes in RAID systems[J]. ACM Trans on Storage, 2014, 10(1): 112-128[11]Plank J S, Blaum M, Hafner J L. SD codes: Erasure codes designed for how storage systems really fail[C]Proc of the 11th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2013: 95-104[12]Li M, Lee P P C. STAIR codes: A general family of erasure codes for tolerating device and sector failures in practical storage systems[C]Proc of the 12th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2014: 147-162[13]Luo Xianghong, Shu Jiwu. Summary of research for erasure code in storage system[J]. Journal of Computer Research and Development, 2012, 49(1):1-11(in Chinese)(罗象宏, 舒继武. 存储系统中的纠删码研究综述[J]. 计算机研究与发展, 2012, 49(1): 1-11)[14]Plank J S, Greenan K M, Miller E L. Screaming fast Galois field arithmetic using Intel SIMD instructions[C]Proc of the 11th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2013: 299-306 Bian Jianchao, born in 1989. PhD candidate. His main research interests include information security, coding theory, storage security and reliability, disaster backup and recovery. Zha Yaxing, born in 1985. PhD candidate. His main research interests include information security, cryptography, storage security and reliability, disaster backup and recovery (zhayaxing@safe-code.com). Luo Shoushan, born in 1962. Professor and PhD supervisor in the School of Computer Science at Beijing University of Posts and Telecommunications. His main research interests include information security, cryptography, secure multi-party computation (luoshoushan@safe-code.com). Li Wei, born in 1986. PhD candidate. His main research interests include information security, cryptography, network security (liwei@safe-code.com). A Hybrid Coding Scheme Based on Intra- and Inter-Device Redundancy Bian Jianchao, Zha Yaxing, Luo Shoushan, and Li Wei (SchoolofComputerScience,BeijingUniversityofPostsandTelecommunications,Beijing100876)(NationalEngineeringLaboratoryforDisasterBackupandRecovery(BeijingUniversityofPostsandTelecommunications),Beijing100876) The development and application of cloud computing set higher requirement for the fault-tolerant capability of the storage systems. Erasure code has been widely used to generate device-level redundancy to protect against device failures, while has less space efficiency when resisting the sector failures. Current optimization schemes for the sector failures only resist the failures of small amounts of the sectors or specific sectors. In this paper, we propose a hybrid coding scheme (intra- and inter-device redundancy, IIDR) combining inter-device redundancy with intra-device redundancy based on the homomorphism property of MDS (maximum distance separable) codes, which employs global parity sector against sector failures in the data disks when adding parity device against device failures, and optimizes the ability to process single-sector errors taking advantage of intra-device coding to generate local parity sectors. In the end, the correctness proof and performance analysis are shown in this paper, and the results indicate that our scheme can protect against device failures and sector failures of any distribution, and the computing cost of recovering single-sector errors is much lower, and the update performance is better. Compared with traditional intra-device coding schemes, our scheme comes with less space usage. cloud computing; device failures; latent sector errors (LSEs); erasure code; intra-disk redundancy 2015-06-16; 2015-10-13 国家“八六三”高技术研究发展计划基金项目(2015AA016005) TP302.8 This work was supported by the National High Technology Research and Development Program of China (863 Program) (2015AA016005).




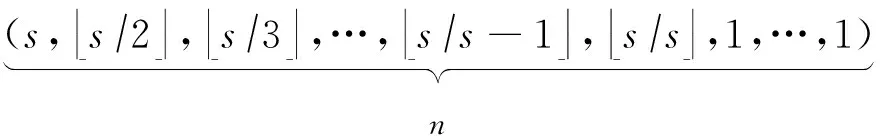
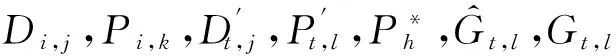

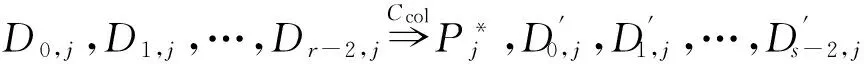

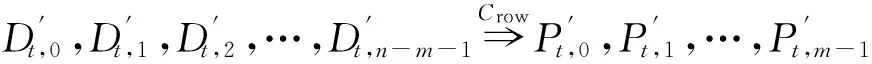


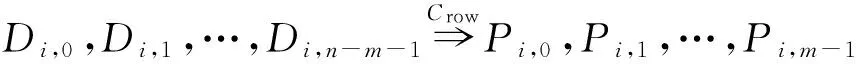
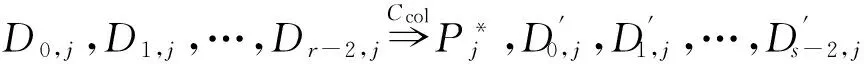


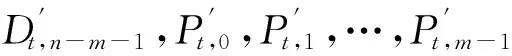






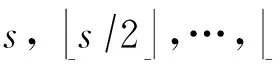






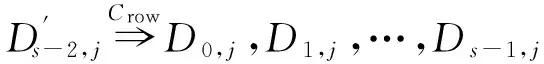
3 正确性证明
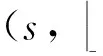



4 性能分析


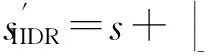


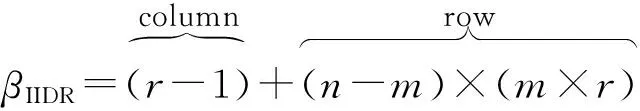






5 结 论




