面向纠删码存储集群的节点并发重构
2016-10-13黄建忠黄思倜谢长生
黄建忠 曹 强 黄思倜 谢长生
(武汉光电国家实验室(华中科技大学) 武汉 430074)
面向纠删码存储集群的节点并发重构
黄建忠曹强黄思倜谢长生
(武汉光电国家实验室(华中科技大学)武汉430074)
(hjzh@hust.edu.cn)
纠删码存储集群的一个关键设计目标是降低重构IO所引起的网络流量,因为降低网络流量有助于缩短重构时间,进而提高可靠性. 针对2个或多个失效节点并发重构这一研究话题,提出一种交叉式重构方案(interleaved reconstruction scheme, IRS).所有替换节点能协同、并行地重构所有失效分块.通过对现有集中式重构方案(centralized reconstruction scheme, CRec)和分散式重构方案(decentralized reconstruction scheme, DRec)的IO流进行分析,分析发现CRec中存储管理器和DRec中替换节点是重构性能的瓶颈. 针对此,IRS从2个方面进行改进:1)替换节点充当重构节点进行并行式重构,消除CRec中管理器这一重构瓶颈;2)利用纠删码的编码结构特性,所有替换节点协同地重构所有失效分块,确保重构时只传输一次所需存活分块.在Reed-Solomon码存储集群上实现了上述3个重构方案,并用真实IO trace进行对比测试. 实验结果表明:当纠删码存储集群的编码参数为k=9和r=3时,IRS方案的双节点重构性能是其他2种重构方案的1.63倍;而3节点重构性能是其他2种重构方案的2.14倍.
纠删编码;集群存储;存储可靠性;节点重构;交叉式重构
分布式存储具有很高的性价比和扩展性,已成为大规模数据中心的主流存储结构.然而,分布式存储系统包含大量存储节点,节点失效是经常性事件.为了避免数据丢失,通常采用副本进行容错.对于PB级以内的数据集而言,3副本方案所增加的2倍存储容量不是太大的问题,但对于PB级、EB级、ZB级存储系统来说,多副本方案的存储开销对硬件成本和运营开支产生巨大压力.而纠删编码具有高容错能力和低存储空间开销的优点[1],已经成为大规模存储的基本容错方案.
近年来纠删码存储研究得到学术界和工业界的广泛关注.国际学术会议(如USENIX FAST,USENIX ATC,IFIP DSN,ACM SOSP等)将纠删码相关研究列为征文主题;同时,出于存储成本和运营开支考虑,一些知名数据中心或云存储系统已大量采用纠删码集群存储方案来存放低访问频度数据(即冷数据),典型案例包括Google第2代文件系统GFS II[2]、微软Azure云存储系统[3]、Facebook部署的HDFS-RAID[4]存储集群.
存储可靠性与修复速度密切相关,对于纠删码存储集群来说,当节点失效时,加速节点恢复是非常重要的[5].研究表明,容r错的纠删码集群存储中,系统MTTDL与节点恢复时间的r次方成反比[6].与此同时,为2个或2个以上节点的并发恢复进行重构优化也是非常必要的:一方面,最近研究表明小型集群系统同一时间发生双节点失效的累计分布函数值CDF大于30%[7];另一方面,为了降低恢复成本,多容错系统会采取“延期修复(delayed repair)”策略[8],即,单节点失效时系统并不即刻启动重构,直至2个或2个以上节点失效时才启动重构过程,避免节点短时失效时导致不必要的频繁重构.
本文对纠删码存储集群下2个及以上并发节点失效重构过程进行优化.通过分析现有重构方案可知,集中式重构方案中管理器节点是重构性能瓶颈;而分散式重构方案中每个替换节点独立请求存活分块,造成同一存活分块的多次传输.本文提出一种交叉式重构方案(interleaved reconstruction scheme, IRS),多个替换节点进行协同重构,并通过互传已重构分块来降低重构流量.
1 背景与相关工作
1.1背景
数据中心通常按容错组方式来组织节点,9~20个节点构成一个容错组,容错组内节点按特定纠删码方案来组织数据放置,构成一个纠删码存储集群[9].以里德所罗门码(Reed Solomon, RS)集群存储为例,文件先分成k个数据分块{D1,1,D1,2,…,D1,k},并按照式(1)所示的冗余矩阵计算得到r个校验分块{P1,1,P1,2,…,P1,r},每个校验分块是k个数据分块的线性组合;k个数据分块及其相应r个校验分块独立地存放到k+r个存储节点{SN1,SN2,…,SNk+r}上,从而得到一种RS(k+r,k)码存储集群.根据RS码的编码特性,该存储集群可容许r个任意节点的同时失效.
(1)
为了避免校验分块的更新访问瓶颈,不同条带上的数据分块和校验分块是分散存储.图1以RS(6,4)码集群存储为例,与RAID5中分散式校验块布局相似,条带1中第1个校验分块P1,1放置在节点SN5上,而条带2中第1个校验分块P2,1放置在节点SN4上.

Fig. 1 Data placement of RS(6,4)-coded storage clusters.图1 RS(6,4)码存储集群的数据放置
为便于描述,本文假设条带总数为N,所有条带都分布在k+r个节点上,并假设重构方案中所有条带采用相同数据布局,即,条带row的k个数据分块{Drow,1,Drow,2,…,Drow,k}和r个校验分块{Prow,1,Prow,2,…,Prow,r}分别存放在节点{SN1,SN2,…,SNk,SNk+1,SNk+2,…,SNk+r}上.
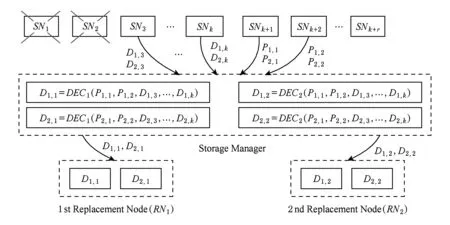
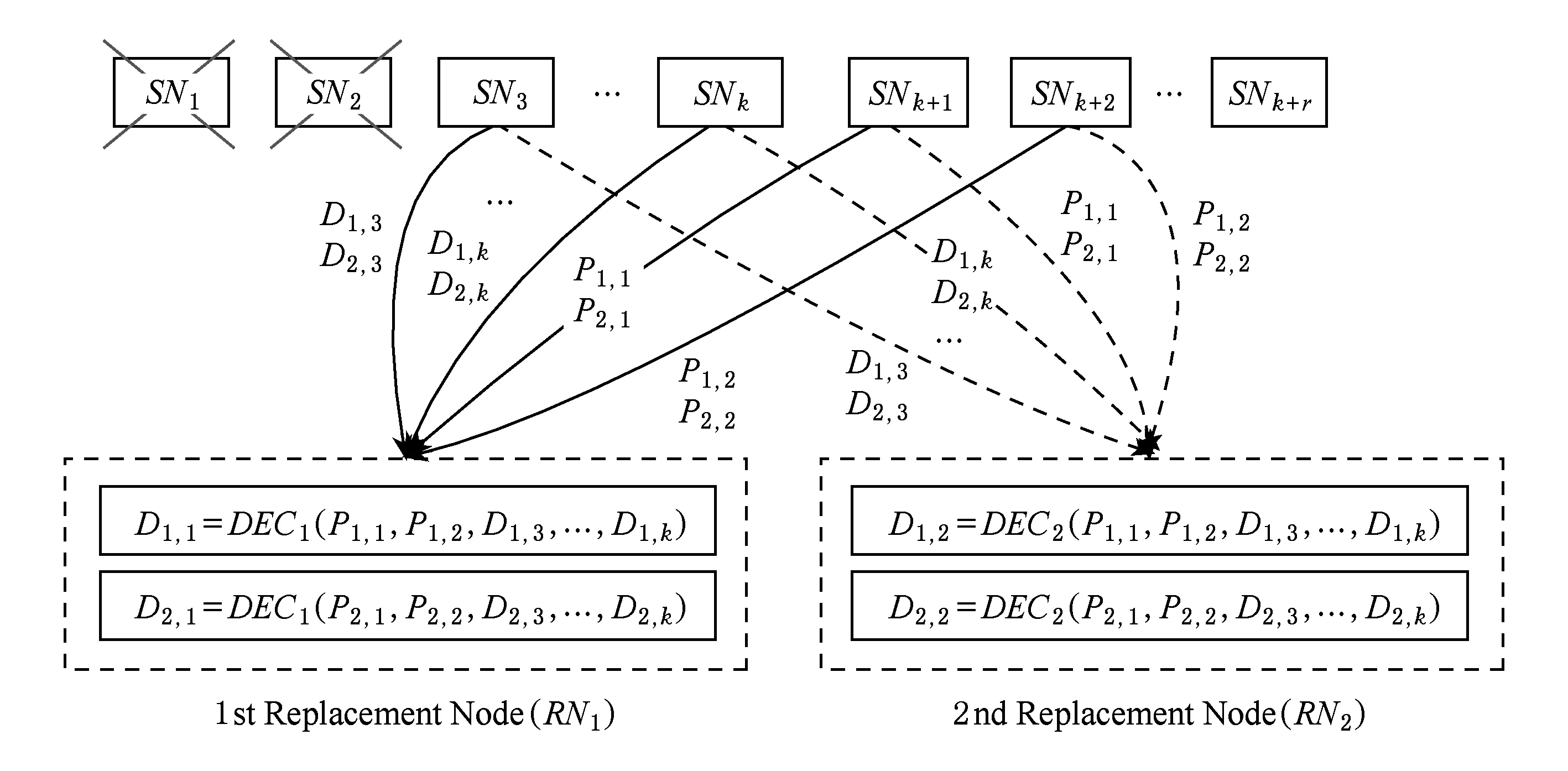
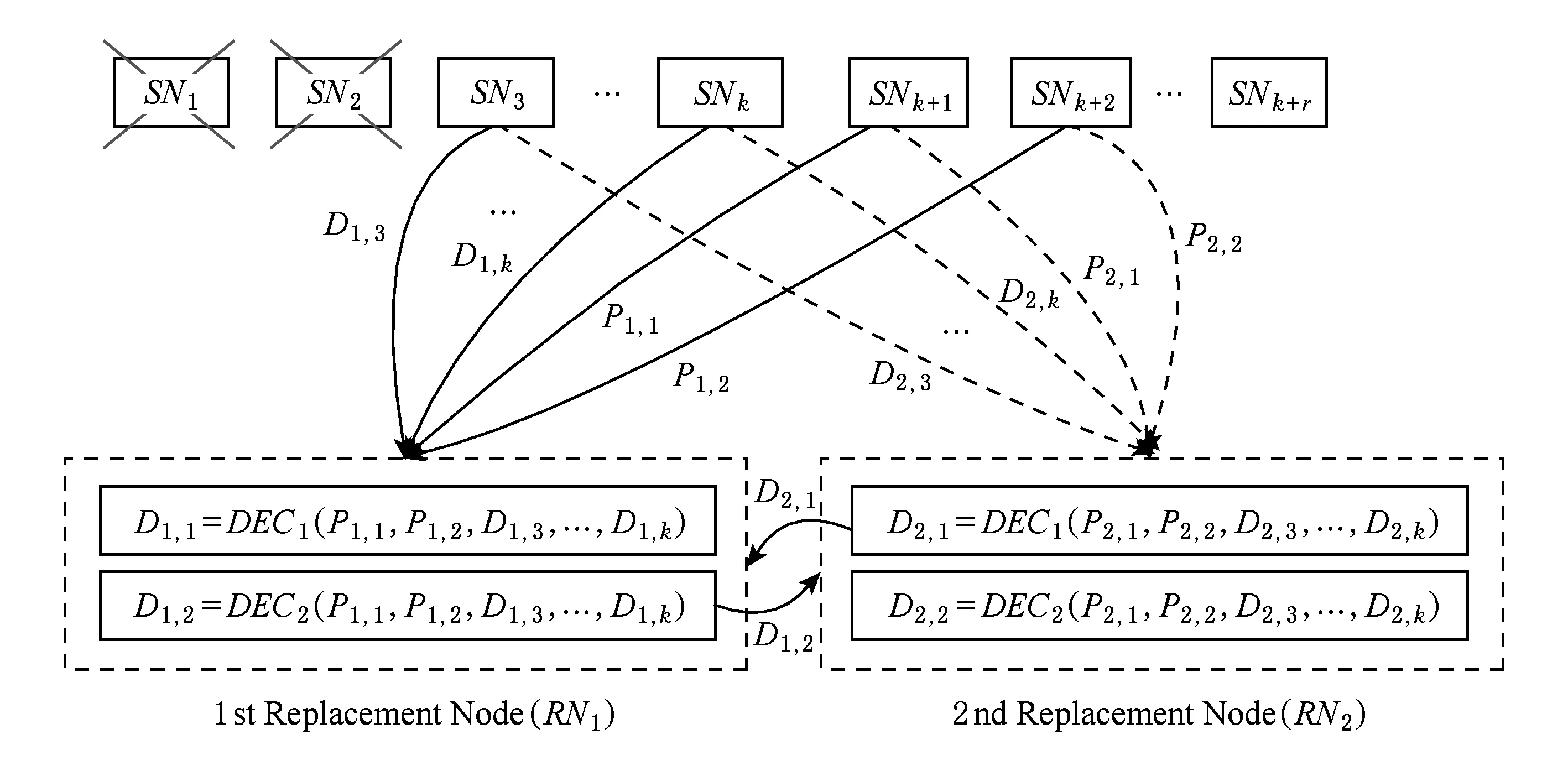
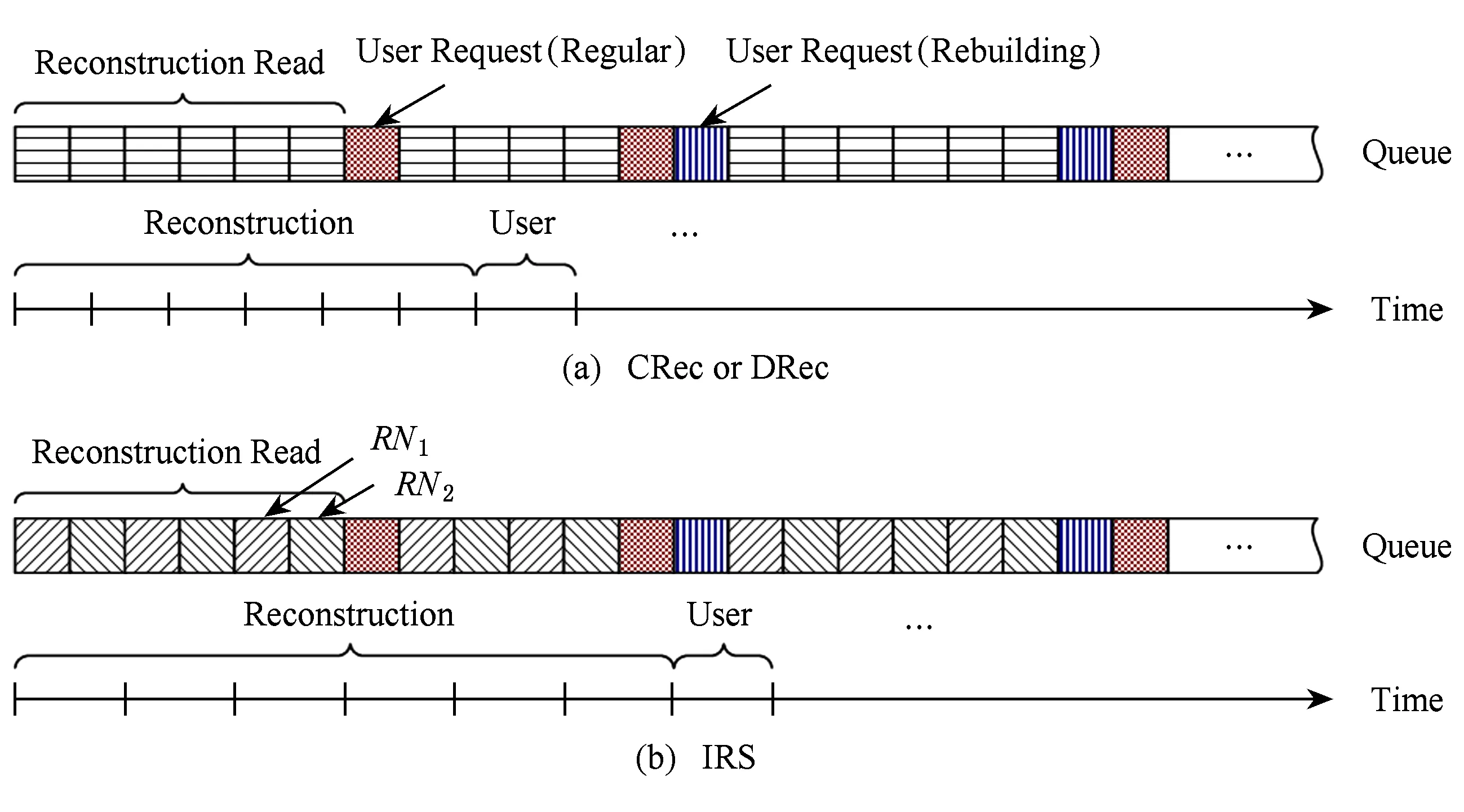
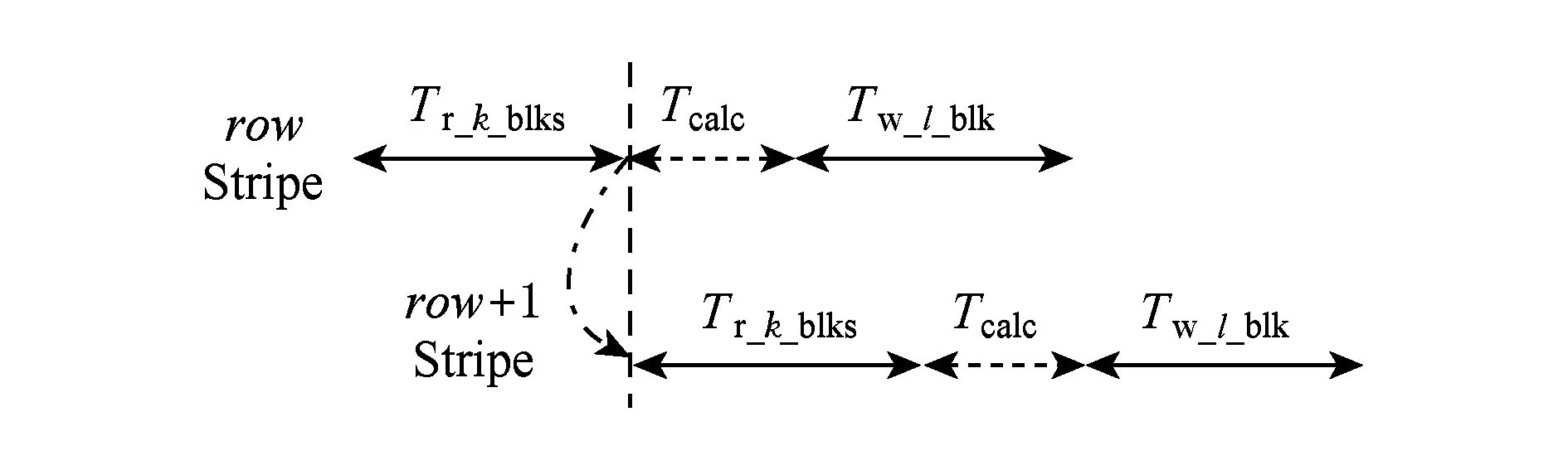
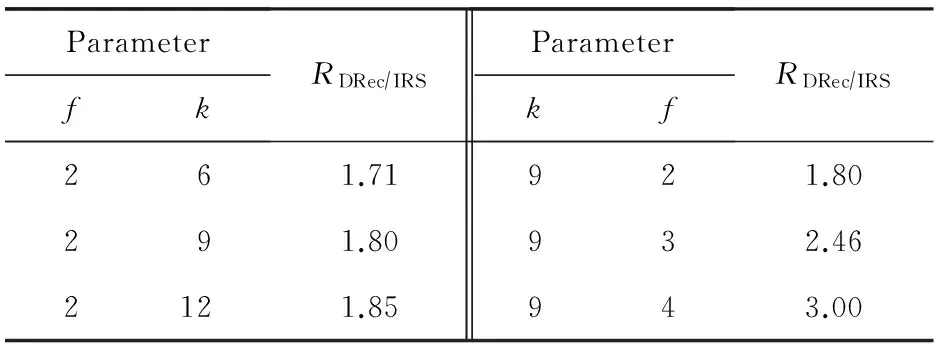
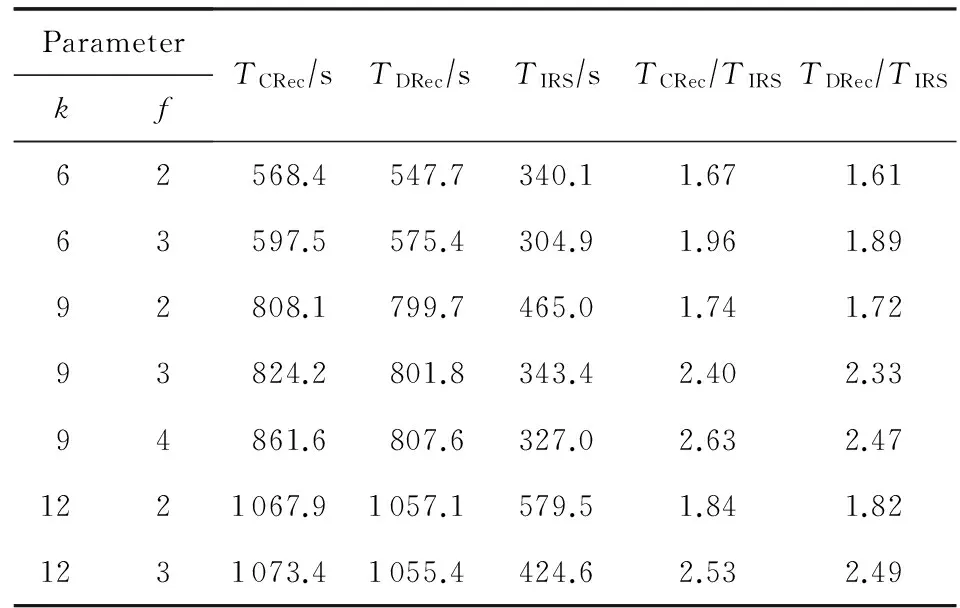
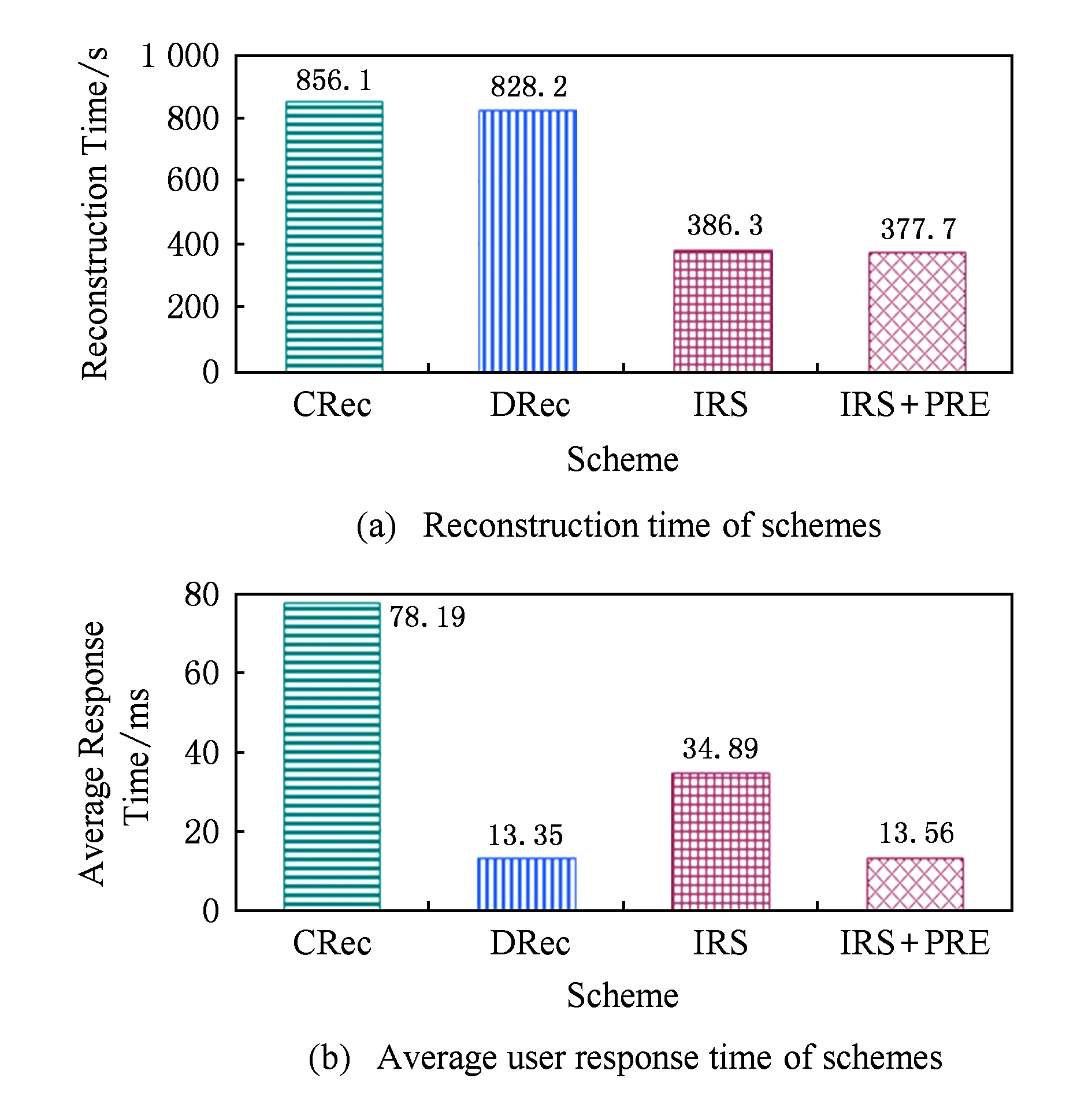
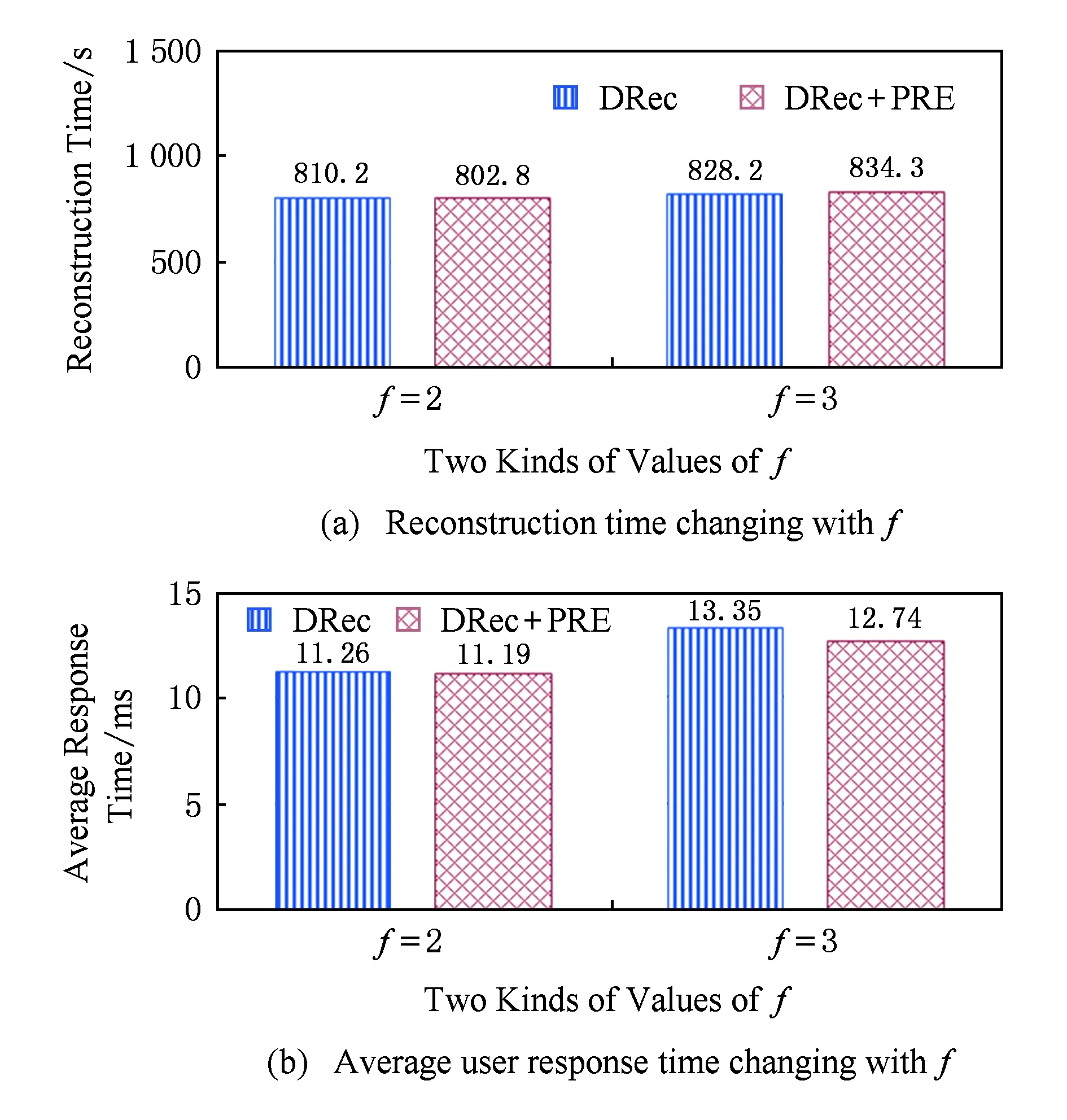
在RS(k+r,k)码集群存储中,当失效节点数f (2) (3) 对式(2)两边同时乘以α2,2,得到式(4): (4) 结合式(3)和式(4),可以推导出式(5) : (5) 同理可以推导出式(6): (6) 根据式(5)和式(6)可知,利用同一row上的k个存活分块{Prow,1,Prow,2,Drow,3,…,Drow,k}可以计算出失效数据分块Drow,1和Drow,2. 1.2相关工作 阵列码是一种特殊的纠删码,其采用简单高效的异或编码运算.对于磁盘阵列中的磁盘失效重构,主要有以下4类优化方法:1) 提高重构并行性,如,DOR让每个存活磁盘都参与重构[10];2) 减少用户IO的干扰,如,WorkOut为了让一个降级RAID将其所有存储资源用于重构,将所有写请求和热度高的读请求外包给一个代理RAID集[11];3) 优化解码操作,如,Hafner等人[12]提出了一种具体的混合重构算法来减少异或操作,降低计算开销以改善解码效率;4) 减少对存活磁盘的读取次数,如,当容双错的RDP磁盘阵列出现单盘失效时,RDOR通过选择最低重构路径,最小化对存活磁盘的读请求数量[13]. 磁盘阵列的故障盘重构只涉及磁盘开销和异或运算开销[14].相对于阵列重构,纠删码存储集群的失效节点恢复显得更加复杂,因为存储集群是通过网络互连,节点重构方案需要考虑磁盘访问、CPU计算和网络传输3方面因素.其中,网络传输往往是节点重构性能的决定性因素.对于纠删码集群存储下的重构优化,目前存在下列4类重构优化方案: 1) 降低校验组规模.为了计算出失效分块,重构节点需要获取k个存活分块,k值越小意味着需要传输的数据量越低.为此,微软Azure云存储系统、Facebook的存储集群同时采用全局校验组和局部校验组(具体方案分别称为局部重构码LRC[3]和局部修复码LRCs[15]),分别为所有数据分块和部分数据分块生成全局校验分块和局部校验分块.重构时可以从局部校验组读取存活数据,相对全局校验组,该方法减少重构所需存活分块的读取数量.这种优化方法的代价是需要占用额外存储空间. 3) 利用修复局部性.Facebook下Hitchhiker系统采用了PiggybackedRS编码[20],PiggybackedRS主要为单一节点失效恢复而优化,该编码利用了修复局部性,减少了恢复时所关联的存活节点数目,以加速重构过程. 纠删码存储重构优化主要围绕编码和存储2个方面展开:1)从编码角度,设计新的纠编码;2)从存储角度,对重构IO进行调度和控制. 表1列出上述所提的几种典型重构优化方案. 本文从IO调度角度对纠删码集群存储进行重构优化. Table 1 Reconstruction Schemes for Erasured-Coded Storage 本文IRS和上述“增加局部校验组”、“基于再生码的重构带宽优化”和“利用修复局部性”3种重构方案都是以“降低网络中数据传输量”为目标导向.但是,这3种重构方案以构建新编码为切入点来研究重构优化,而本文IRS方案从重构IO流层面对存活分块和已重构分块进行调度,以最小化重构流量.特别地,IRS方案可应用于LRC和LRCs中全局校验组或局部校验组上的双节点重构,即,IRS方案与LRC和LRCs是正交的. 集群存储通常部署一个专门的存储管理器来管理所有存储节点.当节点失效时,存储管理器将触发重构操作.如图2所示,按照重构IO流是否经过存储管理器,IO传输可分为带内和带外模式.这里将带内模式和带外模式下重构分别称作集中式重构(centralized reconstruction, CRec)和分散式重构(decentralized reconstruction, DRec). Fig. 2 Transmission mode of reconstruction IOs.图2 重构IO的传输模式 需要说明的是,CRec和DRec这2种重构模式存在于现有重构方案中.例如,重构方案CORE中[19],所有重构操作(包括下载存活分块、解码计算和上传已恢复分块)由Relayer节点集中完成,其属于CRec重构模式;重构方案PiggybackedRS中[20],重构IO流程绕过了存储管理器,一个替换节点(或新节点)专门负责一个失效节点的所有重构操作,该重构属于DRec重构模式.下面以“节点SN1和SN2发生失效”为例来阐述CRec和DRec. 2.1.1CRec方案 在一个RS(k+r,k)码存储集群中,同一条带中k+r个分块中的任意k个分块能够恢复出失效的原始数据分块.CRec中,存储管理器能集中式地计算出失效分块.如图3所示,存储管理器从k个存活节点{SN3,SN4,…,SNk+2}读取2个条带上2×k个存活分块来进行重构,然后再将重构出来的数据分块发送给替换节点RN1和RN2.其中解码函数DEC1(·)和DEC2(·)分别采用式(5)和式(6).CRec方案有着明显的缺点.仅当存储管理器接收到同一条带中k个存活分块后方可进行重构解码计算.当k值增大时,该存储管理器将成为重构过程的性能瓶颈. Fig. 3 Reconstruction flows of CRec.图3 CRec的重构数据流 2.1.2DRec方案 与CRec方案不同,DRec方案将重构操作下放到替换节点来执行,从而解放了管理器节点.图4所示为DRec的重构数据流,为了重构出2个条带中失效分块,2个替换节点RN1和RN2独立地读取多个2×k个存活分块.DRec方案的不足之处是,其需要传输的存活分块数量是CRec的2倍.对于f个节点失效情况,DRec将带来f倍的存活分块网络流量. Fig. 4 Reconstruction flows of DRec.图4 DRec的重构数据流 鉴于CRec单一重构节点瓶颈以及DRec重复传输存活分块这一不足,本文提出一种新的交叉重构方案IRS.IRS能够在提供多个节点并行重构的同时最小化存活分块的传输数量. 2.2IRS重构方案设计 在IRS中,1个条带上的k个存活分块只被一个替换节点读取.图5给出双节点失效时的IRS重构数据流,替换节点RN1读取第1条带的k个存活分块{P1,1,P1,2,D1,3,D1,4,…,D1,k};替换节点RN2读取第2条带的k个存活分块{P2,1,P2,2,D2,3,D2,4,…,D2,k};RN1和RN2继续分别重构第3和第4条带,依此类推.替换节点RN1重构出数据分块D1,1和D1,2;替换节点RN2重构出数据分块D2,1和D2,2.根据RS码存储集群的数据布局,RN1应该保存D1,1和D2,1,而RN2应该保存D1,2和D2,2.于是,RN1将已重构分块D1,2发送给RN2,作为交换,RN1从RN2接收已重构分块D2,1. 算法1描述了f个节点{SN1,SN2,…,SNf}失效时IRS的重构流程.其中,{RN1,RN2,…,RNf}为失效节点{SN1,SN2,…,SNf}所对应的替换节点,1≤f≤r.当f=1时,IRS方案就等同于DRec. Fig. 5 Reconstruction flows of IRS.图5 IRS的重构数据流 算法1. IRS重构流程. ② introw=0; ③ while (row ④ { ⑤ for (inti=1;i≤f;i++){ ⑥RNi读取k个存活分块{Drow+i,f+1,…,Drow+i,k,Prow+i,1,…,Prow+i,f},计算出失效分块{Drow+i,1,Drow+i,2,…,Drow+i,f};} ⑦ for (inti=1;i≤f;i++){ ⑧RNi保留Drow+i,i;并将第row+i条带上f-1个已重构分块{Drow+i,1,Drow+i,2,…,Drow+i,i-1,Drow+i,i+1,…,Drow+i,f}分别发送到其余f-1个替换节点{RN1,RN2,…,RNi-1,RNi+1,…,RNf};} ⑨row=row+f; ⑩ } Fig. 6 Disk request queue in a surviving node.图6 存活节点的磁盘请求队列 当条带总数N不是f的倍数,上述IRS重构算法仍然可用,此时,最后N%f个条带分别由替换节点{RN1,RN2,…,RNN%f}完成重构. 2.3优化用户请求等待时间 用户访问存储集群时,根据用户访问数据的位置可以将用户访问请求分为2类:用户正常请求(请求落在存活节点上)和用户失效请求(请求落在失效节点上).用户失效请求通常转换成对存活节点的修复请求.以用户失效读请求为例,当读请求落在失效节点上,此时需要从k个存活节点读取相应存活分块,再重构出失效请求所需的数据. 在线重构场景下,存活节点要同时响应3种请求:重构读请求、用户正常请求和用户修复请求.图6所示为一个存活节点的在线重构过程中的磁盘请求队列.对比图6(a)和图6(b)可知,相对于CRec和DRec,IRS下存活节点的磁盘将面临2个替换节点RN1和RN2的交叉访问,从而打破了重构读请求的访问顺序性,并延长用户请求等待时间. 为了减轻IRS交叉访问模式对用户访问性能的影响,本文将预取机制引入到重构读操作中,即,在读取某一存活分块时,存活节点读取多个相邻分块并将它们缓存起来,后续的存活分块读请求可直接从缓冲区读取.借助该预取机制,可以增强某一存活节点上对存活分块的读顺序性. 2.4优化同步开销 在IRS重构过程中,一个替换节点需要向其他f-1个替换节点发出读取请求,以获得属于自己的已重构分块,这会带来一个同步的问题.如果这f-1个替换节点中的任意一个暂时没有计算出相应分块,则这次读取请求将停滞,并推迟了重构过程. 针对这种同步延迟,IRS采用持久套接字连接,即,任意2个重构节点之间一旦启动TCP连接,将一直保持该连接,直到所有重构操作结束.从而,每个替换节点能够即时响应其他f-1替换节点的读取请求,任意2个替换节点之间都形成双向数据连接.持久连接有助于优化同步开销的原因如下:1)同步请求的优先级和重构请求的一样高,这样使得同步与重构能够平等地分享网络带宽;2)持久连接使用推传输模式,避免了拉传输模式的读取停滞问题. 3.1符号定义 本节对3种重构方案的重构进行建模.重构的过程主要分为3个阶段: 阶段1. 重构节点从存活节点读取k个存活分块.CRec的重构节点是管理器本身;DRec和IRS的重构节点是替换节点.这个阶段的耗时用Tr_k_blks表示.本阶段中,k个存活分块需要从网线传到网卡的传输缓冲区中,从而包含串行延迟. 阶段2. 重构节点利用存活分块解码出失效分块,用时记为Tcalc. 阶段3. 将已重构分块写入到替换节点.CRec中,该过程包含管理器节点将已重构分块发送给替换节点,由替换节点写入磁盘的过程.DRec中,即为替换节点将已重构分块写入到本地磁盘的过程. IRS中,该写入过程包含多个替换节点相互传输已重构分块并写入各自磁盘的过程.重构节点发送m个已重构分块的用时记为Ts_m_blks,替换节点写入m个已重构分块的用时记为Tw_m_blks. 3.2CRec重构时间 Fig. 7 Analysis of reconstruction time in CRec.图7 CRec重构时间分析 图7绘出CRec方案中各阶段的耗时示意图. 管理器节点耗时Tr_k_blks接收完当前条带的k个存活分块,耗时Tcalc计算出失效分块,再耗时Ts_f_blks将f个已重构分块发送给替换节点.这里假设Ts_f_blks包含替换节点接收数据并写入本地磁盘的时间.从而,CRec重构一个条带的时间为 (7) (8) 其中,S为节点重构时的条带数. 3.3DRec重构时间 与CRec不同,DRec使用替换节点而非管理器节点来完成重构过程.图8所示为DRec方案中各阶段的耗时示意图. Fig. 8 Analysis of reconstruction time in DRec.图8 DRec重构时间分析 DRec中,每个替换节点只重构对应的失效分块,不需要为其他f-1替换节点完成重构操作,因此重构一个条带的用时为 (9) 式(9)等号右边前2项和式(7) 前2项相同,而式(9)中第3项Tw_1_blk表示将一个已重构分块写入本地磁盘的时间.在DRec中,每个替换节点只写入当前条带的1个已重构分块. 与CRec相似,DRec也是在接收了当前条带的k个存活分块之后立刻启动下一个条带的重构,所以总重构时间TDRec约等于总条带数与接收1个条带中k个存活分块用时的乘积. 如式(10)所示,TDRec与TCRec在形式上相等. (10) 3.4IRS重构时间 IRS方案中,每个替换节点需要从存活节点读取k个存活分块;此外,IRS中1个替换节点从其余f-1替换节点接收f-1个已重构分块,并向它们各发送一个已重构分块.由于替换节点需要互传已重构分块,因此存在一定的同步开销,图9绘出IRS方案中一个替换节点所经历的各阶段操作. Fig. 9 Analysis of reconstruction time in IRS.图9 IRS重构时间分析 在接收k个存活分块后,某替换节点一边接收来自其他f-1个替换节点的已重构分块(时间为Tr_f-1_blks),一边计算失效分块(时间为Tcalc),并将其中f-1个已重构分块分别给其他f-1替换节点(时间为Ts_f-1_blocks).在计算出失效分块或接收到已重构分块时,该替换节点可以向本地磁盘写入已重构分块,总共要写入f个已重构分块(时间为Tw_f_blks).所以一个条带的重构时间可表示为 (11) 如式(11),TIRS_stripe考虑了同步延迟Tsync,因为每一个替换节点在发送f-1已重构分块的同时也在接收其他f-1个替换节点的已重构分块.既然f个替换节点同时重构f个条带,某一替换节点在重构完第row条带之后,就可以开始重构第row+f条带,所以IRS总重构时间为 TIRS=(Tr_k_blks+Tsync+Ts_f-1_blks)×Sf. (12) 由式(12)可知,每个替换节点平均完成Sf个条带的重构,这是IRS能够加速重构的原因. 3.5定量化验证 用R表示DRec和IRS重构时间的比值.从式(10)和式(12)可以得出: (13) 理想情况下,IRS的替换节点之间没有同步延迟,即Tsync=0.另外,重构过程中重构流量非常大,k个分块的传输时间可视为1个分块传输时间的k倍.从而,式(13)可以进一步简化为 (14) 表2列出了DRec和IRS在不同k值和f值下的理论重构时间比.其中,R随着失效节点数f的增大而明显增加. Table 2Theoretical Ratio of Reconstruction Time Between DRec and IRS 表2 DRec与IRS的理论重构时间比值 图10给出了不同参数下理论重构时间比和实测重构时间比,其中重构时间实测值来自表3. 从图10可以观察到:1)重构时间比的理论值与实测值在f不变而k变化情况下相差不大(见图10(a)),原因在于当f=2时,替换节点RN1只需和另一替换节点RN2交换已重构分块,引起很低的同步开销Tsync;2)在k不变而f变大时理论值和实测值之间差距在增大(见图10(b)),原因在于同步开销随着f增大而增加,而理论重构时间比值将同步开销忽略不计.通过对比图10中重构时间理论对比值与实测对比值,很大程度上能反映出上述CRec,DRec,IRS方案的重构时间模型的正确性. 此外,从图7~9可以看出,仅当重构节点(即CRec中的管理器节点、DRec和IRS中的替换节点)接收到存活分块或已重构分块后,该重构节点方可进行下一条带的重构,这意味着重构节点的网络接收带宽将是整个重构过程的性能瓶颈. 4.1实验环境 本实验集群存储采用RS码,集群拥有15个存储节点和1个客户端服务器.所有机器通过思科千兆以太网交换机互连.每个存储节点包含1个英特尔E5800@3.2GHz处理器和1个型号为WD1002FBYS的SATA2磁盘.客户端服务器是一个浪潮服务器,包含2个X5650@2.80 GHz的4核处理器,12 GB容量的DDR3主存.所有机器采用2.6.32内核版本的Linux操作系统.客户端服务器通过播放IO Trace来模拟多并发用户访问;另外,在CRec重构方案中,该服务器也充当管理器节点的角色. 4.2原型系统与测试方法 RS码的编解码操作使用Zfec库[22]实现.在重构过程中,重构节点向k个存活节点发送分块读请求,以读取k个存活分块,并重构出失效分块. 在线重构中,需要同时模拟重构过程和用户访问行为.为了测量用户响应时间,在存储集群上实现了应用层的trace播放器.如果请求数据位于失效节点上,trace播放器将直接发送k个读请求给k个存活节点,以获取k个存活数据.将IO trace限定于读访问的原因在于纠删码集群存储主要应用于数据归档,而归档是一种一次写多次读的IO应用.本文使用Web-2 trace[23]这一读密集型IO trace,该trace被广泛地用来评估在线重构技术的性能[11,24-25]. 重构测试时将失效节点存储容量限制为10 GB,这个数据量足够覆盖trace负载的访问范围.离线重构测试关注重构时间这一性能指标;在线重构性能则包括重构时间和平均用户响应时间.进行每个测试项之前,清空缓存;所有测试项重复测试5次,计算各测试值的平均值. 4.3实验结果与分析 4.3.1离线重构 Table 3Comparison of Off-line Reconstruction Performance of three Schemes 表3 3种重构方案的离线重构性能比较 通过分析表3实验数据,可得到如下结论: 1) 相比CRec和DRec,IRS拥有最短重构时间.以参数k=9,f=2为例,IRS对CRec和DRec的加速比分别为1.74和1.72.原因在于:当f个节点需要重构时,CRec和DRec下每个重构节点需要接收k×10 GB的存活分块;而在IRS中,每个替换节点只需要接收(kf)×10 GB的存活分块和(1-1f)×10 GB的已重构分块. 2) 参数k和f在不同数值组合下,CRec和DRec的重构时间相差不大,这个实验结果与重构时间模型中式(10)“TDRec=TCRec”是一致的.一方面,在一定程度上验证了上述重构时间模型的正确性;另一方面,相对于CRec的集中式重构策略,DRec的分散式重构策略也无法提升重构性能,这也凸显了IRS中交叉式重构策略的优越性. 4.3.2在线重构 图11给出了RS(12,9)码存储集群在2个节点失效时在线重构的测试结果.其中,IRS+PRE表示采用预取机制的IRS方案.对于f节点失效重构,预取存活分块的数量为f-1,即,在进行双节点重构时,存活节点需要预取1个存活分块. Fig. 11 Performance of double-node on-line reconstruction.图11 双节点在线重构性能 CRec,DRec,IRS在参数k=9,f=2下的离线重构时间分别808.1 s,799.7 s,465.0 s,如表3所示;而3种方案在在线重构下的重构时间分别为816.8 s,810.2 s,497.4 s,如图11(a)所示.一方面,说明在线重构时间大于离线重构时间,原因如下:这3种重构方案都需要经历“从k个存活节点读取k个存活分块”这一节点,仅当接收到k个存活分块,重构节点才进行解码计算,在线重构时存活节点的IO带宽被用户IO和重构请求共同占用,用户IO将对重构请求造成干扰,这会影响到“重构节点读取k个存活分块”请求的响应,最后导致时间Tr_k_blks的增加;另一方面,相对于离线重构时间,在线重构时间有少量增加,原因在于3种重构方案的重构性能瓶颈是重构节点的网络接收带宽,而磁盘IO带宽竞争无法对重构时间造成很大影响. Fig. 12 Performance of triple-node on-line reconstruction.图12 3节点在线重构性能 从图11(b)可知,在IRS在线重构时,预取机制能同时改进重构性能和用户访问性能,因为预取机制能将存活节点磁盘的顺序读合并在一起,减少了磁盘在重构请求和用户请求之间的切换次数,因而获得比原先更好的用户响应和重构响应.综合来讲,IRS+PRE能获得最优的重构时间,同时能达到与DRec相近的平均用户响应时间. 图12所示为RS(12,9)码存储集群在3个节点失效时在线重构的测试结果.其中,IRS+PRE表示采用预取机制的IRS方案;在进行3节点重构时,存活节点需要预取2个存活分块. 对比图11和图12可知,随着失效节点数f从2变为3时,IRS的重构时间有很大降低,原因是多了一个替换节点参与重构,单个替换节点承担的重构流量减少了.当纠删码存储集群的编码参数为k=9时,IRS方案的双节点在线重构性能至少是其他2种重构方案的1.63倍;而3节点在线重构性能是其他2种重构方案的2.14倍. 4.3.3预取机制 4.3.2节验证了预取机制能够改进IRS方案的重构性能和用户访问性能.CRec方案中存活节点能以连续读方式响应管理器节点的重构读请求,即CRec能获得读连续性.DRec方案中f个替换节点会发出重构读请求,请求一个存活节点上的同一存活分块, 因此需要评估预取机制对DRec性能的影响.图13为DRec在线重构性能,其中,DRec+PRE表示采用预取机制的DRec方案,参数k=9. Fig. 13 On-line reconstruction performance of DRec.图13 DRec在线重构性能 从图13可知,一方面,不管是否采用预取机制,DRec方案的重构时间变化不大.原因在于,当每个替换节点向某一存活节点发出读请求以读取某一存活分块时,该存活分块会自动缓存到该存活节点的缓冲区中,所缓存的存活分块可以响应其他f-1个替换节点的读请求,从逻辑上讲,它同样达到了数据预取效果;另一方面,预取机制对DRec 方案的平均用户响应时间有少许优化作用. 对于RS(k+r,k)码存储集群来说,为了保障能够恢复出失效节点上的失效分块,必须保证失效节点数f不大于容错数r,即f≤r.随着失效节点数f的增加,有更多替换节点参与重构,这样的话,每个重构节点需要重构的条带数量将减少. 图1中,所有条带的k+r分块分别放置到k+r存储节点上,该k+r个节点构成一个容错组.在实际集群中,不同条带可放置在不同的容错组上,这种情况下CRec,DRec,IRS方案的重构性能将保持不变,因为重构节点仍旧要读取k个存活分块,同时,重构节点接收带宽是重构性能瓶颈. 当不同条带放置在不同的容错组时,失效节点上的失效分块可能是数据分块,也可能是校验分块,此时需要调整相应的重构解码函数. 从IRS重构时间模型可知,重构节点的接收带宽通常决定了整体重构过程的性能,这意味着存活节点仍然拥有可用带宽,从而,预取机制通常能达到预期效果;但在特殊情况下,如用户IO和重构IO竞争带宽,造成存活节点的可用带宽不足,此时将影响到预取操作,针对此,可以将重构IO的请求设为高优先级. 针对纠删码存储集群中2个及2个以上节点失效,本文提出一种能有效降低重构流量的交叉式重构方案——IRS.IRS方案中,不同替换节点分别重构不同条带上的失效分块,然后通过交换已重构分块来完成所有失效分块的重构.本文为3种重构方案建立了重构时间模型,并用实测数据定量化验证了模型正确性,模型揭示了“重构节点的网络接收带宽是重构性能瓶颈”这一结论.在真实存储集群下测试了重构方案,对比测试结果表明:一方面,IRS能够大幅度地减少重构流量,进而提升并发节点重构性能;另一方面,存活分块预取机制能有效增强重构读请求的访问顺序性,并提升用户访问性能. 在建立重构时间模型时,本文仅仅分析了重构过程中的3个基本操作:计算、IO和传输;而在实际系统中,重构过程涉及多任务排队处理和随机过程,我们拟在未来工作中考虑这些因素,以完善3种重构方案的重构时间模型;另外,为了能全面评估和分析重构性能影响因素,需要实测TCP连接、解码运算、多任务切换等性能开销. [1]Fan B, Tantisiriroj W, Xiao L, et al. Diskreduce: Replication as a prelude to erasure coding in data-intensive scalable computing[C]Proc of 2011 Int Conf for High Performance Computing Networking, Storage and Analysis. New York: ACM, 2011: 6-10[2]Ford D, Labelle F, Popovici F, et al. Availability in globally distributed storage systems[C]Proc of the 9th Symp on Operating Systems Design and Implementation(OSDI 2010). Berkeley, CA: USENIX Association, 2010: 61-74[3]Huang C, Simitci H, Xu Y, et al. Erasure coding in windows azure storage[C]Proc of the 2012 USENIX Annual Technical Conf (ATC 2012). Berkeley, CA: USENIX Association, 2012: 15-26[4]Thusoo A, Shao Z, Anthony S, et al. Data warehousing and analytics infrastructure at Facebook[C]Proc of the 2010 ACM SIGMOD Int Conf on Management of Data(SIGMOD 2010). New York: ACM, 2010: 1013-1020[5]Luo Xianghong, Shu Jiwu. Summary of research for erasure code in storage system[J]. Journal of Computer Research and Development, 2012, 49(1): 1-11 (in Chinese)(罗象宏, 舒继武. 存储系统中的纠删码研究综述[J]. 计算机研究与发展, 2012, 49(1): 1-11)[6]Rao K, Hafner J, Golding R. Reliability for networked storage nodes[J]. IEEE Trans on Dependable and Secure Computing, 2011, 8(3): 404-418[7]Schroeder B, Gibson G. A large-scale study of failures in high-performance computing systems[J]. IEEE Trans on Dependable and Secure Computing, 2011, 7(4): 337-350[8]Bhagwan R, Tati K, Cheng Y, et al. Total recall: System support for automated availability management[C]Proc of the 1st Symp on Networked Systems Design and Implementation (NSDI 2004). Berkeley, CA: USENIX Association, 2004: 337-350[9]Calder B, Wang J, Ogus A, et al. Windows azure storage: A highly available cloud storage service with strong consistency[C]Proc of the 23rd ACM Symp on Operating Systems Principles (SOSP 2011). New York: ACM, 2011: 143-157[10]Holland M, Gibson G, Siewiorek D. Architectures and algorithms for on-line failure recovery in redundant disk arrays[J]. Distributed and Parallel Databases, 1994, 2(3): 295-335[11]Wu S, Jiang H, Feng D, et al. Workout: IO workload outsourcing for boosting RAID reconstruction performance[C]Proc of the 7th USENIX Conf on File and Storage Technologies(FAST 2009). Berkeley, CA: USENIX Association, 2009: 239-252[12]Hafner J, Deenadhayalan V, Rao K. Matrix methods for lost data reconstruction in erasure codes[C]Proc of the 4th USENIX Conf on File and Storage Technologies(FAST 2005). Berkeley, CA: USENIX Association, 2005: 183-196[13]Xiang L, Xu Y, Lui J, et al. Optimal recovery of single disk failure in RDP code storage systems[J]. ACM SIGMETRICS Performance Evaluation Review, 2010, 38(1): 119-130[14]Kenchammana-Hosekote D, He D, Hafner J. REO: A generic RAID engine and optimizer[C]Proc of the 5th USENIX Conf on File and Storage Technologies(FAST 2007). Berkeley, CA: USENIX Association, 2007: 261-276[15]Sathiamoorthy M, Asteris M, Papailiopoulos D, et al. XORing elephants: Novel erasure codes for big data[C]Proc of the 39th Int Conf on Very Large Data Bases. New York: ACM, 2013: 325-336[16]Wei Dongsheng, Li Jun, Wang Xin. Performance study of exact minimum bandwidth regenerating codes in distributed storage[J]. Journal of Computer Research and Development, 2014, 51(8): 1671-1680 (in Chinese)(卫东升, 李钧, 王新. 分布式存储中精确修复最小带宽再生码的性能研究[J]. 计算机研究与发展, 2014, 51(8): 1671-1680)[17]Dimakis A, Godfrey P, Wu Y, et al. Network coding for distributed storage systems[J]. IEEE Trans on Information Theory, 2010, 56(9): 4539-4551[18]Wu Y, Dimakis A. Reducing repair traffic for erasure coding-based storage via interference alignment[C]Proc of the 2009 IEEE Int Symp on Information Theory. Piscataway, NJ: IEEE, 2009: 2276-2280[19]Li R, Lin J, Lee P. CORE: Augmenting regenerating-coding-based recovery for single and concurrent failures in distributed storage systems[C]Proc of the 29th IEEE Conf on Massive Data Storage. Piscataway, NJ: IEEE, 2013: 1-6[20]Rashmi K, Shah N, Gu D, et al. A hitchhiker's guide to fast and efficient data reconstruction in erasure-coded data centers[C]Proc of the 2014 ACM Conf on SIGCOMM. New York: ACM, 2014: 331-342[21]Huang J, Liang X, Qin X, et.al. PUSH: A pipelined reconstruction IO for erasure-coded storage clusters[J]. IEEE Trans on Parallel and Distributed Systems, 2015, 26(2): 516-526[22]Wilcox-O’Hearn Z. Zfec 1.4.2[CPOL]. 2011[2014-09-01]. http:pypi.python.orgpypizfec [23]Liberatore M. Search engine IO[OL]. 2007 [2014-10-01]. http:traces.cs.umass.edu[24]Wan S, Cao Q, Huang J, et al. Victim disk first: An asymmetric cache to boost the performance of disk arrays under faulty conditions[C]Proc of the 2011 USENIX Annual Technical Conf(ATC 2011). Berkeley, CA: USENIX Association, 2011: 173-186[25]Tian L, Feng D, Jiang H, et al. PRO: A popularity-based multi-threaded reconstruction optimization for RAID-structured storage systems[C]Proc of the 5th USENIX Conf on File and Storage Technologies(FAST 2007). Berkeley, CA: USENIX Association, 2007: 301-314 Huang Jianzhong, born in 1975. Received his PhD degree from the Huazhong University of Science and Technology in 2005. Associate professor. His main research interests include computer architecture,networked storage and dependable storage. Cao Qiang, born in 1975. Received his PhD degree from the Huazhong University of Science and Technology in 2003. Professor and PhD supervisor. His main research interests include computer architecture, large-scale storage, and power-efficient storage. Huang Siti, born in 1989. Received his master degree from the Huazhong University of Science and Technology in 2015. His main research interests include dependable storage and distributed file system. Xie Changsheng, born in 1957. Received his master degree from the Huazhong University of Science and Technology in 1982. Professor and PhD supervisor. His main research interests include computer architecture, IO system, networked storage, ultra-density optical storage technology, and so on. Concurrent Node Reconstruction for Erasure-Coded Storage Clusters Huang Jianzhong, Cao Qiang, Huang Siti, and Xie Changsheng (WuhanNationalLaboratoryforOptoelectronics(HuazhongUniversityofScienceandTechnology),Wuhan430074) A key design goal of erasure-coded storage clusters is to minimize network traffic incurred by reconstruction IOs, because reducing network traffic helps to shorten reconstruction time, which in turn leads to high system reliability. An interleaved reconstruction scheme (IRS) is proposed to address the issue of concurrently recovering two and more failed nodes. With analyzing the IO flows of centralized reconstruction scheme (CRec) and decentralized reconstruction scheme (DRec), it is revealed that reconstruction performance bottleneck lies in the manager node for CRec and replacement nodes for DRec. IRS improves CRec and DRec from two aspects: 1) acting as rebuilding nodes, replacement nodes deal with reconstruction IOs in a parallel manner, thereby bypassing the storage manager in CRec; 2) all replacement nodes collaboratively rebuild all failed blocks, exploiting structural properties of erasure codes to transfer each surviving block only once during the reconstruction process, and achieving high reconstruction IO parallelism. The three reconstruction schemes (i.e., CRec, DRec, and IRS) are implemented under (k+r,k) Reed-Solomon-coded storage clusters where real-world IO traces are replayed. Experimental results show that, under an erasure-coded storage cluster with parametersk=9 andr=3, IRS outperforms both CRec and DRec schemes in terms of reconstruction time by a factor of at least 1.63 and 2.14 for double-node and triple-node on-line reconstructions, respectively. erasure codes; clustered storage; storage reliability; node reconstruction; interleaved reconstruction 2015-01-23; 2015-08-11 国家自然科学基金项目(61572209);国家“八六三”高技术研究发展计划基金项目(2013AA013203);国家“九七三”重点基础研究发展计划基金项目(2011CB302303) 曹强(caoqiang@hust.edu.cn) TP333 This work was supported by the National Natural Science Foundation of China (61572209), the National High Technology Research and Development Program of China (863 Program) (2013AA013203), and the National Basic Research Program of China (973 Program) (2011CB302303).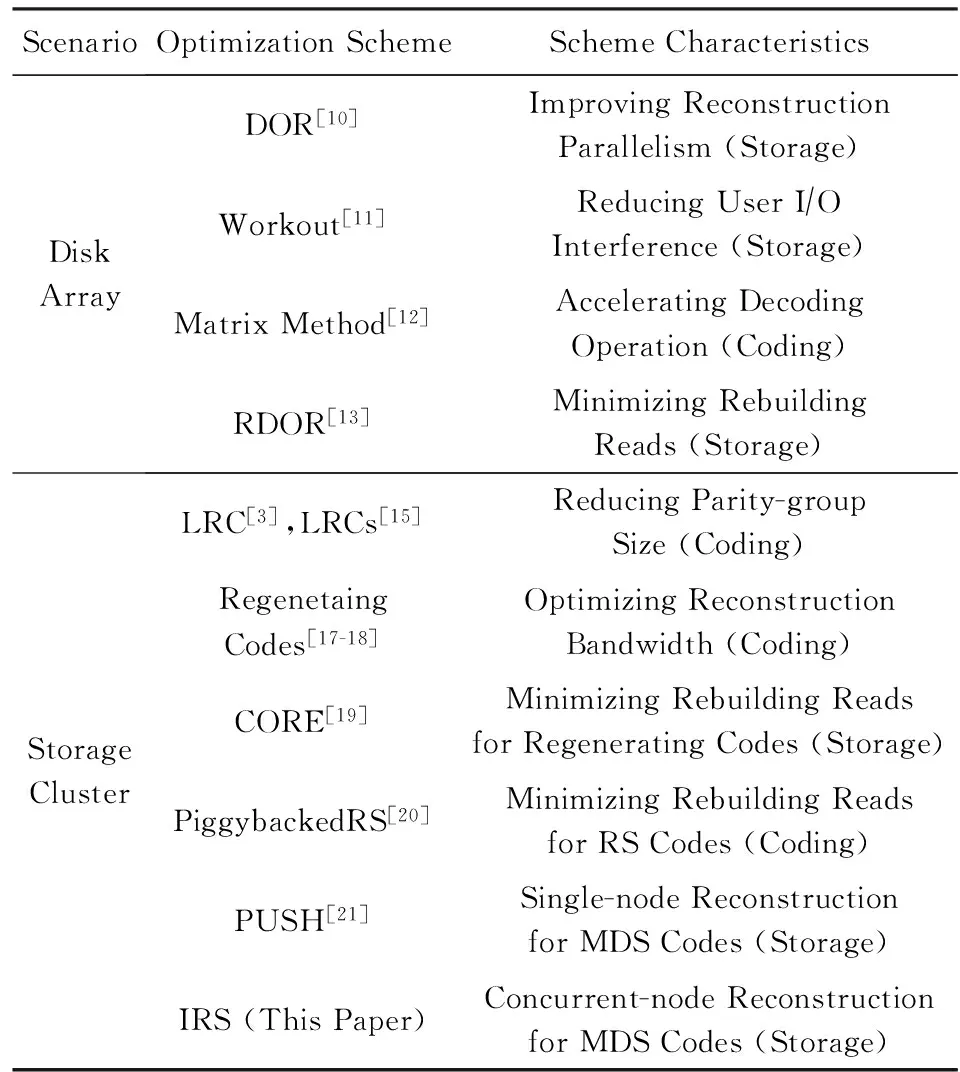
2 针对多节点失效的交叉重构方案

3 重构时间模型






4 实验评估

5 方案适用性分析
6 结论和展望




