简化Bishop 法的剩余下滑推力计算方法研究*
2019-10-26杨红娟钱江澎
刘 茂 杨红娟 钱江澎
( ①四川省地质工程勘察院 成都 610072)
( ②成都理工大学核技术与自动化工程学院 成都 610059)
0 引 言
英国著名土力学家毕肖普( Bishop A W) 于1955 年发表了圆弧条分法在土质边坡稳定性中的应用一文,Bishop 法由此正式诞生。Bishop( 1955)考虑条块间力的作用,假设条间力为水平力,条块土体界面上的剪应力不能超过该界面的最大抗剪强度值,该法根据每个条块的竖向力平衡条件和整体力矩平衡条件( 所有条块所受作用力的力矩之和为0)推导出来的,由于条块间切向力为未知量,Bishop A W 进一步假设ΔHi= Hi+1- Hi= 0,得到了简化Bishop 法,简化Bishop 法( John Krahn,2004; 李广信等,2013) 满足力多边形闭合条件。
国内外很多学者( Duncan,1996; 陈祖煜,2003; 郑颖人等,2007; 苏爱军,2008) 对边坡稳定分析方法的计算精度进行了讨论和分析,简化Bishop 法计算出的圆弧滑动面安全系数与严格条分法( 如Morgenstern-Price 法和Spencer 法) 的安全系数十分接近,一般误差只有3%~4%,甚至在1%以内。当时,简化Bishop法也可以看成严格条分法。Duncan( 1996) 认为简化Bishop 法在所有情况下都是精确的( 除了遇到数值分析困难情况外) ,其局限性表现在仅适用于圆弧滑裂面以及有时会遇到数值分析问题( 当mai=cosαi+sinαitanφi/Fs<0.2,可以认为简化Bishop 法中存在数值分析问题) 。
朱大勇等( 2007) 对简化Bishop 法的严格性进行了论证分析,简化Bishop 法满足所有平衡条件;刘茂( 2011) 对各种稳定性计算方法进行了总结,张年学等( 2018) 认为条间剪力对其没有明显影响,邓涛等( 2019) 基于通用条分原理,采用微分形式的土条受力平衡推导出了锚框支护边坡地震动力稳定分析方法。简化Bishop 法被公认为是一个计算圆弧形滑面稳定性的简便、精确的方法,该稳定性计算方法已被广泛应用于圆弧形滑面的稳定性分析中,但却没有比较简易的剩余下滑推力解析方法,本文从简化Bishop 法基本原理出发,利用力多边形法则,推导出基于简化Bishop 法的剩余下滑推力解析计算方法。
1 条块i 的下滑推力模型
根据简化Bishop 法的假设条件,条块i 受力模型如下:

图1 条块i 的受力模型Fig. 1 The force model acting on slice i
根据条块所受外力方向、条块倾角、条块所受力的固有特征,利用力多边形法则和单个条块处于静力平衡条件可知,单个条块力多边形模型可分为两种模型( Ⅰ型和Ⅱ型) 。
Ⅰ型为条块所受抗滑力方向与坡向相反,再根据条块i 的力多边形模型,Ⅱ型可具体分为Ⅱ1型( 多边形模型水平力之和大于等于0( 图2 b、图2d) ) 和Ⅱ2型( 多边形模型水平力之和小于0( 图2a、图2c) ) ,典型模型见图2。
具体模型表达式如下:
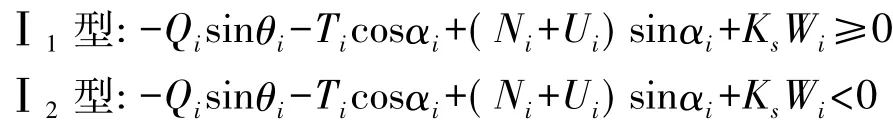
Ⅱ型为条块所受抗滑力方向与坡向相同,再根据条块i 的力多边形模型,Ⅰ型可具体分为Ⅰ1型( 多边形模型水平力之和大于等于0( 图3 b、图3d) ) 和Ⅰ2型( 多边形模型水平力之和小于0( 图3a、图3c) ) ,典型模型见图3。
具体模型表达式如下:
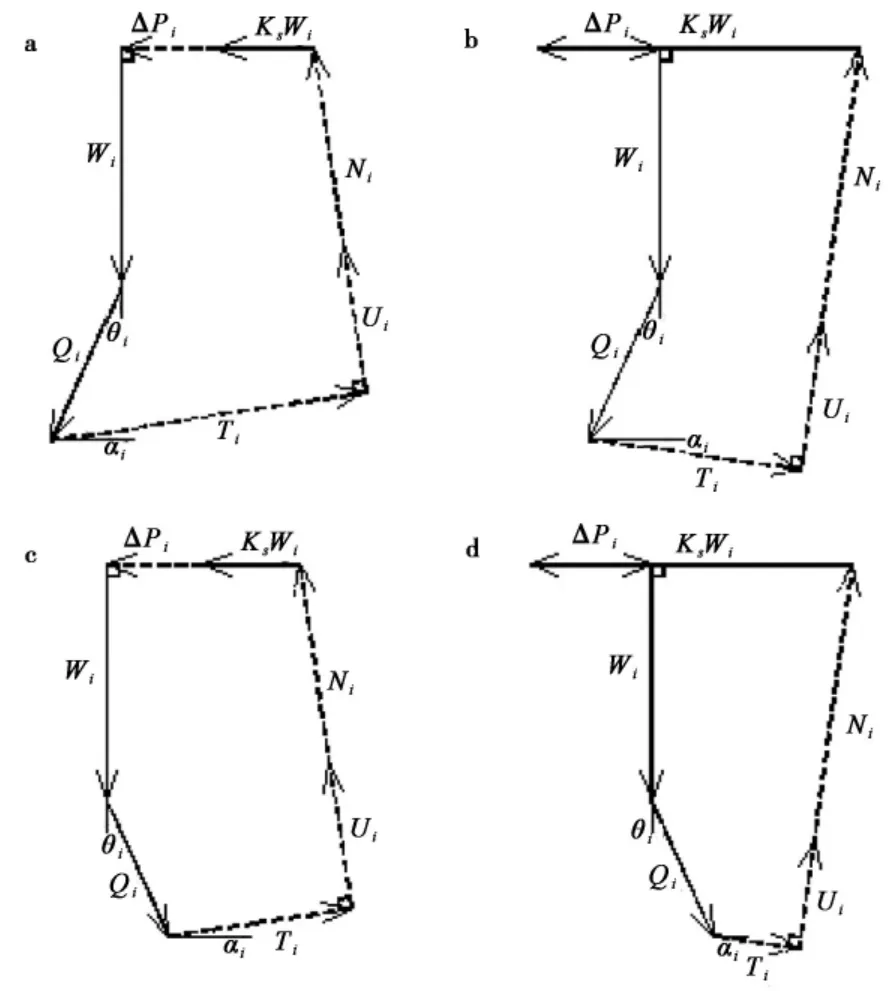
图2 典型受力模型( Ⅰ型)Fig. 2 The typical force model of slice i( model Ⅰ)
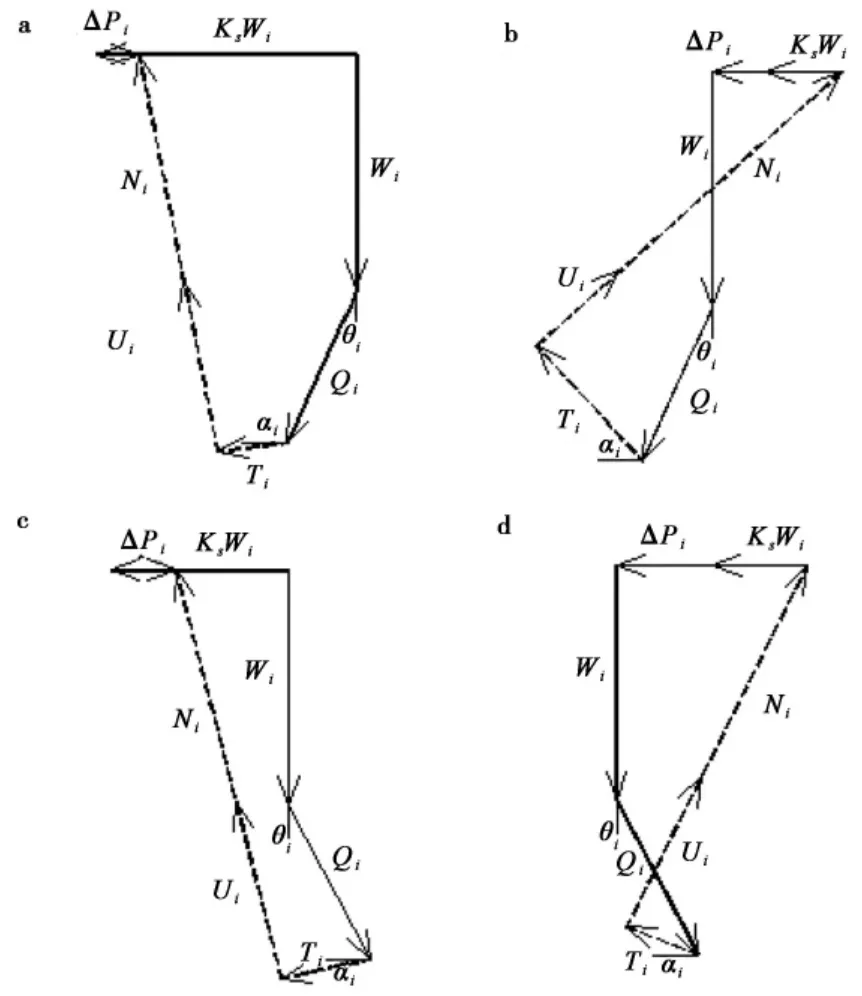
图3 典型受力模型( Ⅱ型)Fig. 3 The typical force model of slice i( model Ⅱ)
Ⅱ1型:
-Qisinθi+Ticosαi+( Ni+Ui) sinαi+KsWi≥0
Ⅱ2型:
-Qisinθi+Ticosαi+( Ni+Ui) sinαi+KsWi<0
上述模型表达式中,Qi为外力( kN·m-1) ( 顺时针为正,逆时针为负) ,Wi为条块 i 的重 力( kN·m-1) ,Ti为条块i 的抗滑力( kN·m-1) ( 与坡向相同为负,与坡向相反为正) ,Ni为条块i 的垂直压力( kN·m-1) ,Ui为条块i 的孔隙水压力( kN·m-1) ,Ks为水平加速度系数( g) ,αi为条块i 的滑动面倾角( 与坡向相同为正,与坡向相反为负) ,θi为条块i所受外力的倾角( 顺时针为负,逆时针为正) 。
2 简化Bishop 法剩余下滑推力解析方法
根据上述条块i 作用力的力多边形模型可知,对于条块i,根据力多边形法则,考虑垂直方向力的平衡时有:
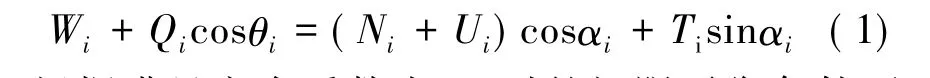
根据满足安全系数为Fs时的极限平衡条件可得:
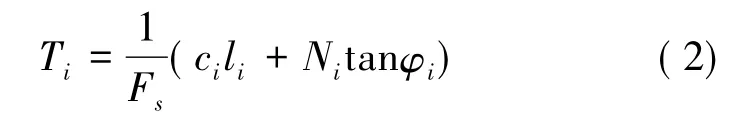
将式( 2) 代入式( 1) ,整理后可得:
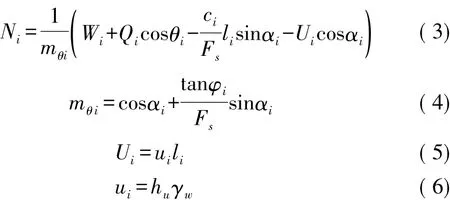
计算剩余下滑推力时,还必须满足一定规定,规定如下:
(1) 土体抗拉强度很弱,可忽略不计,因此,剩余下滑推力不能为负值,若为负值时取为0。
(2) 上一条块的剩余下滑推力直接作用于相邻下一条块上,作用方向为水平。
根据以上规定和两种模型可知,条块i 的剩余下滑推力Fi的解析表达式为式( 7) :
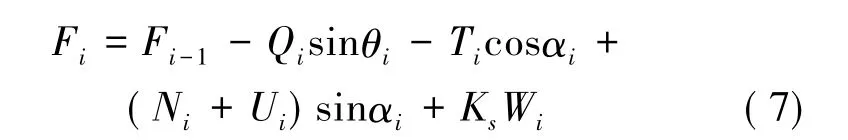
当Fi小于等于0 时,条块i 的剩余下滑推力为0,但剩余下滑力计算过程中不取0,按照实际计算值进行计算。
当Ti指向坡向方向时取负值,否则为正,Ti的判据表达式见式( 8) 。
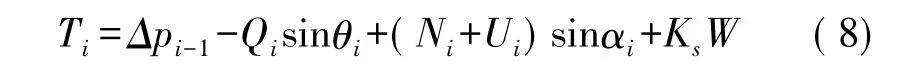
其余公式和符号同上。
3 简化Bishop 法剩余下滑推力与传递系数法隐式解剩余下滑推力比较与讨论
3.1 圆弧形滑面模型
如图4 所示的某圆弧滑动面的滑坡,该圆弧形滑动面滑坡模型数据见表1。
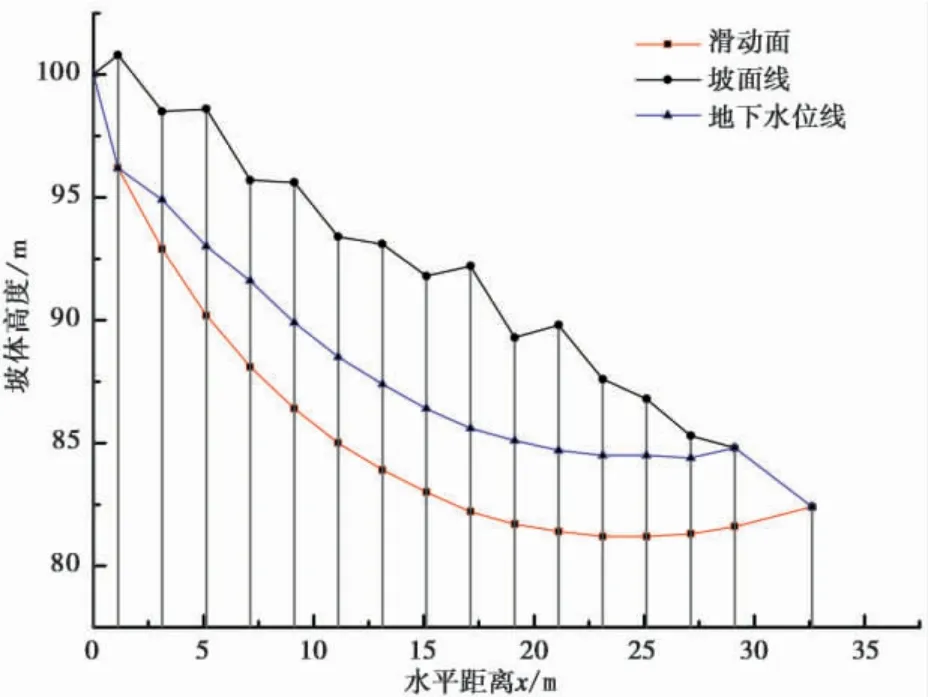
图4 圆弧滑动面滑坡模型Fig. 4 Landslide model of the slip circle
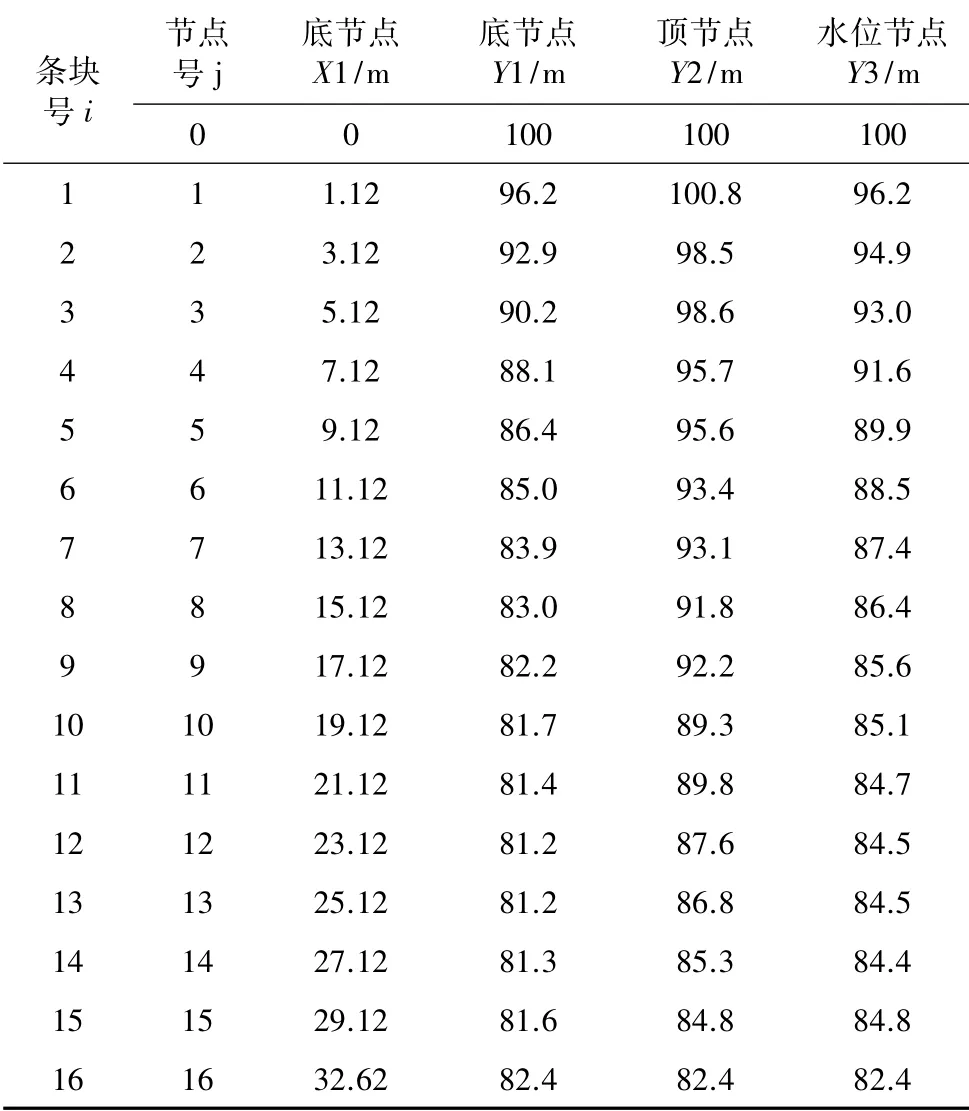
表1 圆弧滑动面滑坡模型数据Table 1 The data of landslide model of the slip circle
3.2 剩余下滑推力对比分析
两种方法的剩余下滑推力计算,模型采用上述圆弧形滑动面滑坡模型,滑体天然重度为19.6 kN·m-3,饱和重度为20.1 kN·m-3,内黏聚力为18 kPa,内摩察角为15°,分别得到各个安全系数ks=1.00 ~1.35 安全储备下的剩余下滑推力,剩余下滑推力曲线如图5、图6。
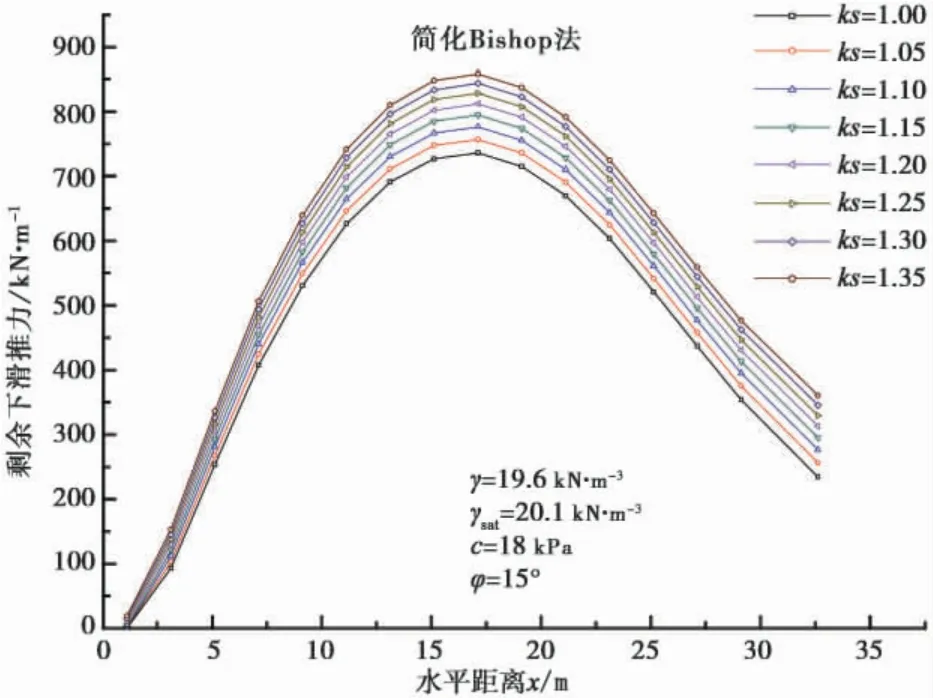
图5 简化Bishop 法剩余下滑推力曲线Fig. 5 The curve map of residual sliding force based on simplified Bishop method
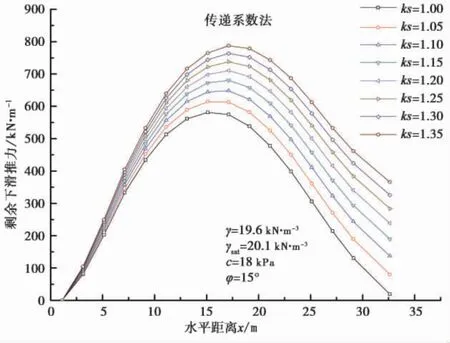
图6 传递系数法剩余下滑推力曲线Fig. 6 The curve map of residual sliding force based on transfer coefficient method
由图5 和图6 可知,简化Bishop 法剩余下滑推力最大值部位几乎不随安全系数变化,几乎位于坡体的中部部位条块,传递系数法隐式解剩余下滑推力最大值随着安全系数增大从坡体中上部向坡体中部迁移,但出现最大值的条块范围分布范围较小;整个坡体条块的剩余下滑推力趋势与传递系数法隐式解基本一致。
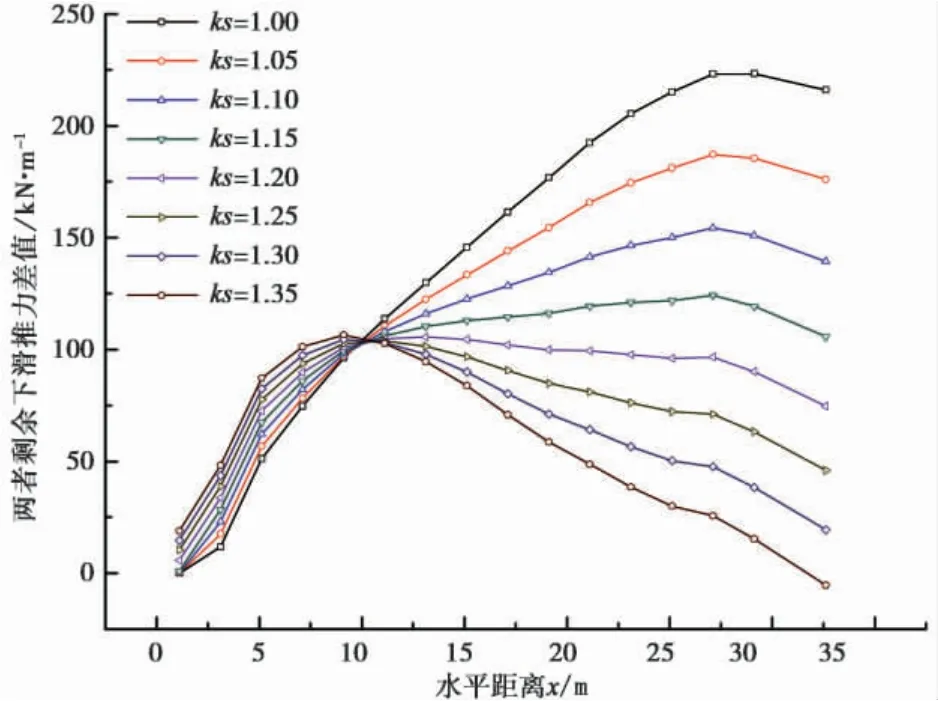
图7 剩余下滑推力差值曲线Fig. 7 The difference curve map of residual sliding force between the simplified Bishop method and transport coefficient method
简化Bishop 法剩余下滑推力比传递系数法隐式解剩余下滑推力大,两者的剩余下滑推力差值在坡体的中上部( 约坡体的1/3) 随着水平距离增大而增大,随着安全系数增大,两者的差值在减小; 安全系数为ks=1.0~1.15 时,坡体中部和中下部差值随着安全系数增大差值呈增大的趋势,只是在最后1~2 个条块趋于减少趋势,安全系数为ks=1.15 ~1.35时,坡体中部和中下部差值随着安全系数增大差值呈减小的趋势。
由图8、图9 可知,简化Bishop 法相邻条块剩余下滑推力增量趋势是一致的,从上往下总体呈现上升-下降-平缓-下降的趋势,但是,简化Bishop 法相邻条块剩余下滑推力增量在坡体上部( 1/3 部分) 随着安全系数升高而增大,坡体其余部位几乎不随安全系数变化而变化,而传递系数法相邻条块剩余下滑推力增量各个条块间随着安全储备的增大而增大,坡体中部基本上呈现线形增加。
由图10 可知,简化Bishop 法剩余下滑推力比传递系数法隐式解剩余下滑推力大,整个坡体条块剩余下滑推力的平均值在坡体的中上部( 1/3 部位) ,简化Bishop 法较传递系数法隐式解整个坡体条块剩余下滑推力的增加百分比平均值一般可增加15%~35%,最大可增加45%,且随着安全储备增大,整个坡体条块剩余下滑推力的增加百分比平均值在减小。
当ks<1.25 时,增加百分比从坡顶至坡脚呈增加-减少-平缓-快速增加的趋势,且增加或减少的幅度随着安全系数增加而减小; 当ks>1.25 时,增加百分比从坡顶至坡脚呈快速减少-减小的趋势,且减少的幅度随着安全系数增加而减小。
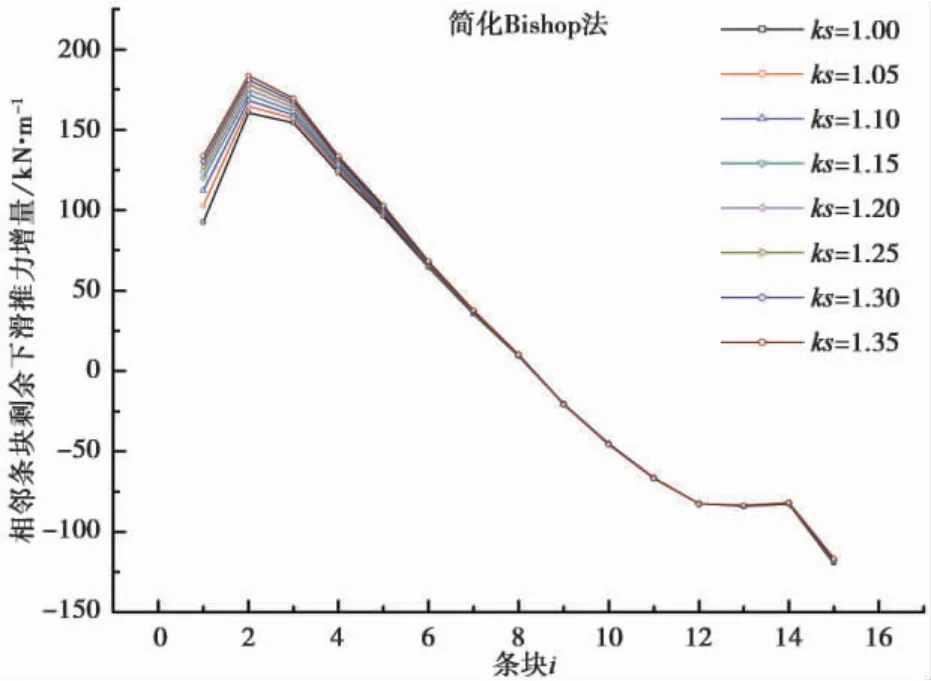
图8 简化Bishop 法相邻条块剩余下滑推力增量曲线Fig. 8 The residual slope thrust increment curve of adjacent bars by simplified Bishop method
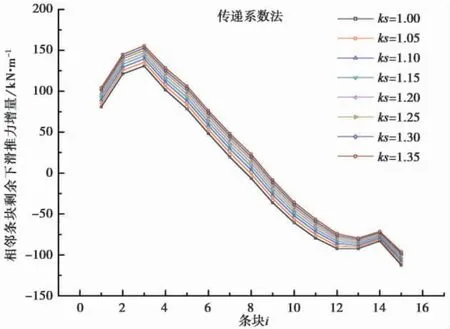
图9 传递系数法相邻条块剩余下滑推力增量曲线Fig. 9 The residual slope thrust increment curve of adjacent bars by transfer coefficient method
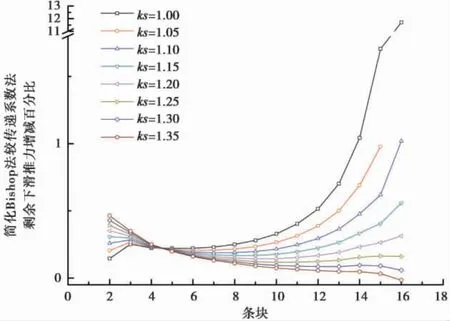
图10 剩余下滑推力增减百分比曲线Fig. 10 The percentage increase curve map of residual sliding force when compared to transport coefficient method
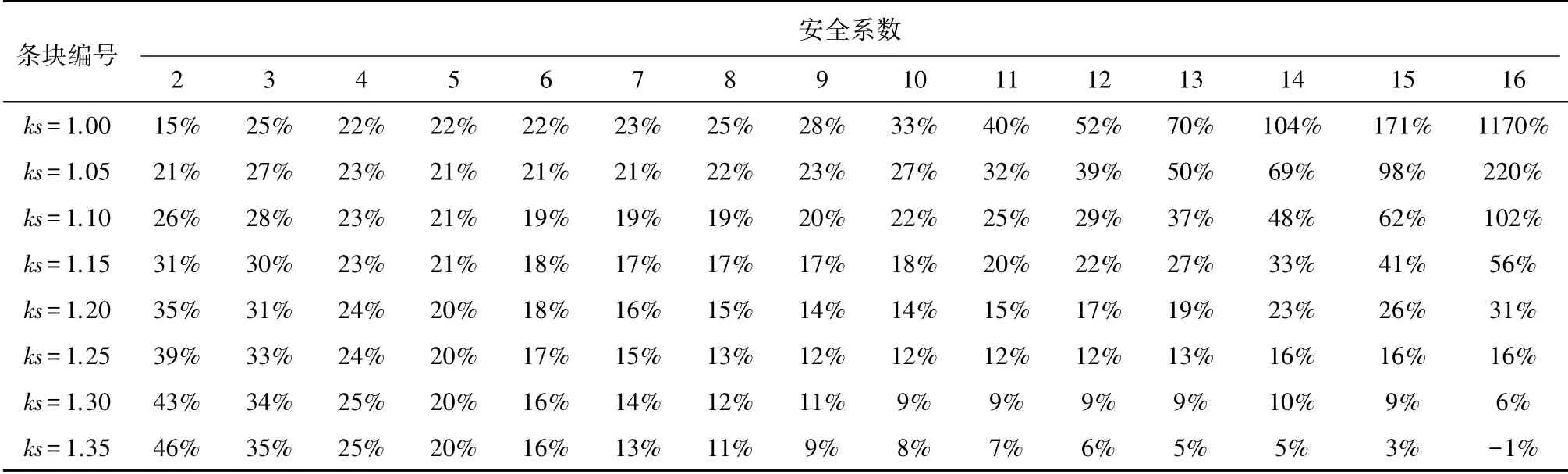
表2 剩余下滑推力增减百分比Table 2 The percentage increase of residual sliding force when compared to transport coefficient method
当安全系数较小( ks<1.1) 时,坡体最后1 ~4 个条块推力增幅较大,一般可增幅70%~100%,最大可增幅约10 倍甚至更大,该方法对于安全系数较小的边坡最后几个条块的剩余下滑推力有待进一步分析研究。
3.3 剩余下滑推力对比结果分析探讨
针对以上剩余下滑推力的对比分析,总体上呈现出简化Bishop 法剩余下滑推力高于传递系数法隐式解的剩余下滑推力,增大的幅度也不同,分析探讨如下:
( 1) 对于同一个滑坡( 边坡) ,两种计算稳定性的方法不一致,由于两种稳定性计算方法都有其局限性,简化Bishop 法主要适用于圆弧形滑面滑坡,且只考虑条间力方向为水平方向,传递系数法主要受相邻条块倾角差和突变的影响,且滑面倾角不宜过大,评价出的滑坡( 边坡) 稳定性不同,安全系数和稳定系数的差值,即安全储备大小影响剩余下滑推力值。
(2) 简化Bishop 法剩余下滑推力比传递系数法隐式解剩余下滑推力大,究其原因在于简化Bishop法本身忽略了条块间的竖向摩擦力,而传递系数法考虑了条块间的竖向摩擦力,且考虑了相邻条块滑面倾角的影响。
( 3) 随着安全储备的增大,两者的剩余下滑推力差值减小,原因在于这两种计算方法都为隐式解法,同时折减c、tanΦ,安全系数变大,条块的垂直压力减小,下滑力增大可减少条块间的相互影响,可减小两者剩余下滑力的差值。
4 算 例
本次选取一个经典算例进行简化Bishop 法和传递系数法剩余下滑推力比较,边坡剖面和土层参数( 图11) ,该边坡假设为永久边坡,边坡的安全等级为一级边坡,取稳定安全系数为ks=1.35,计算得到简化Bishop 法和传递系数法剩余下滑推力值( 图12) 和两者的剩余下滑推力增减百分比曲线( 图13) 。
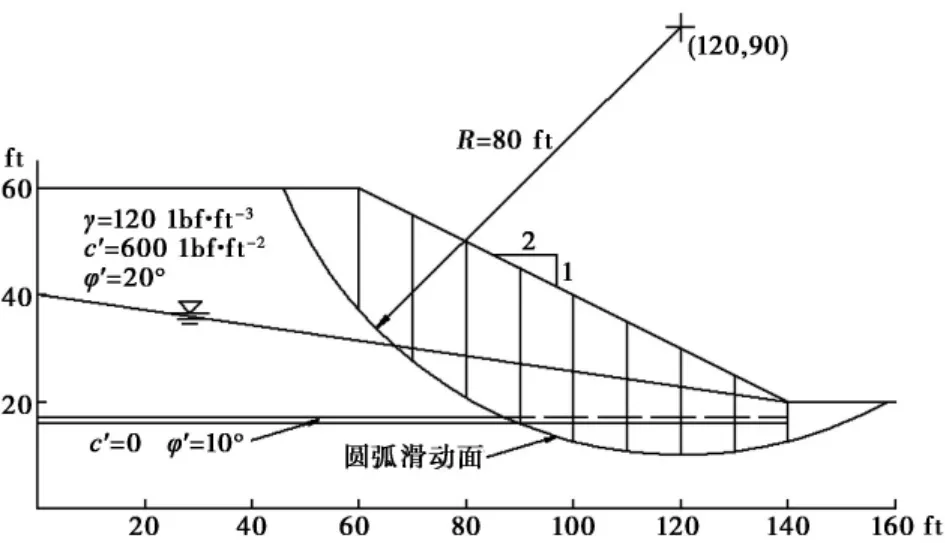
图11 典型算例的地质剖面图Fig. 11 The geological profile of a typical example
5 结 论
( 1) 评价圆弧形滑动面滑坡时,简化Bishop 法是一种公认精确、简便的“严格”方法,该方法在我国被普遍应用,但却没有与之相适应的剩余下滑推力解析计算方法。
( 2) 根据条块的受力条件、力的多边形法则和Ti的方向( 指向坡向方向时取负值,否则为正) ,把单个条块力多边形模型分为两类:Ⅰ型( Ti≥0) 和Ⅱ型( Ti<0) ,依据上述两类模型,利用条块垂直力平衡和极限平衡条件以及条块水平力平衡推导出了剩余下滑推力的解析计算公式。
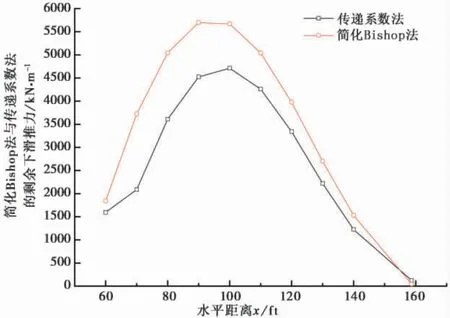
图12 简化Bishop 法和传递系数法剩余下滑推力曲线Fig. 12 The curve map of residual sliding force based on simplified Bishop method and transfer coefficient method
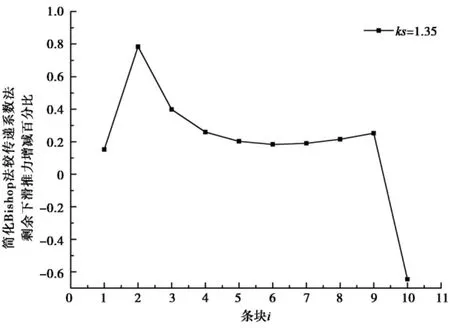
图13 典型算例剩余下滑推力增减百分比曲线Fig. 13 The difference curve map of residual sliding force between the simplified Bishop method and transport coefficient method about typical example
(3) 简化Bishop 法和传递系数法隐式解剩余下滑推力比较可知,简化Bishop 法剩余下滑推力比传递系数法隐式解剩余下滑推力大,简化Bishop 法整个坡体条块剩余下滑推力的增加百分比平均值一般可增加15%~35%,最大可增加45%,且随着安全储备增大,整个坡体条块剩余下滑推力的增加百分比平均值在减小。当安全系数较小( ks<1.1) 时,坡体最后1~4 个条块推力增幅较大,一般可增幅70%~100%,最大可增幅约10 倍甚至更大,该方法对于安全系数较小的滑坡( 边坡) 最后几个条块的剩余下滑推力有待进一步分析研究。
( 4) 该剩余下滑推力解析法为隐式解法,且隐式解法属于强度储备系数法,该方法比较符合滑坡( 边坡) 下滑破坏的规律,为圆弧形滑动面滑坡( 边坡) 的剩余下滑推力提供了一定的理论依据。
