具有程序的静态结构和动态行为语义的时序逻辑
2016-10-13陈冬火金海东
陈冬火 刘 全,2 金海东 朱 斐,2 王 辉
1(苏州大学计算机科学与技术学院 江苏苏州 215006)2 (符号计算与知识工程教育部重点实验室(吉林大学) 长春 130012)
具有程序的静态结构和动态行为语义的时序逻辑
陈冬火1刘全1,2金海东1朱斐1,2王辉1
1(苏州大学计算机科学与技术学院江苏苏州215006)2(符号计算与知识工程教育部重点实验室(吉林大学)长春130012)
(dhchen@suda.edu.cn)
提出一种区间分支时序逻辑——控制流区间时序逻辑(control flow interval temporal logic, CFITL),用于规约程序的时序属性.不同于计算树逻辑(computation tree logic, CTL)和线性时序逻辑(linear temporal logic, LTL)等传统的时序逻辑,CFITL公式的语义模型不是基于状态的类Kripke结构,而是以程序的抽象模型控制流图(control flow graph, CFG)为基础所构建的含序CFG结构.含序CFG是CFG的一种受限子集,它们的拓扑结构可映射为偏序集,这样诱导产生的自然数区间可自然地用于描述定义良好的程序结构. 这种结构含有程序的静态结构信息和动态行为信息,换而言之,CFITL具有规约程序实现结构属性和程序执行动态行为属性的能力.在定义CFITL的语法和语义的基础上,详细讨论了CFITL的模型检验问题,包括基于值状态空间可达性计算的模型检验方法和基于SMT(satisfiability modulo theories)的CFITL有界模型检验方法. 现代程序都含有复杂且具有无限值域的抽象数据类型及各种复杂的操作,CFITL语义定义相比CTL等时序逻辑更复杂,因此,基于显示状态搜索的方法难以有效进行,而基于SMT的CFITL有界模型检验方法更易实现、更具有可行性.最近开发相关的原型工具,并进行相关的实例研究.
区间时序逻辑; 控制流程图; 程序静态结构;模型检验;可满足性模理论
时序逻辑是一种模态逻辑,广泛用于描述和推理各种计算机系统状态随时间演化所应满足的性质,例如计算树逻辑(computation tree logic, CTL)[1]、线性时序逻辑(linear temporal logic, LTL)[2]、概率计算树逻辑(probabilistic computation tree logic, PCTL)[3]和连续时间随机逻辑(continuous time stochastic logic, CSL)[4]等.各种时序逻辑具有足够的表达能力,能用于描述各类计算机系统包括安全性属性及活性属性的各类性质.自从20世纪80年代模型检验[5]思想提出以来,基于时序逻辑的模型检验方法成为形式化验证领域的重要研究方向[6-11].有别于传统的测试方法,模型检验方法用算法自动检测系统的行为(数学结构)是否满足某条属性(时序逻辑公式),并且当系统不满足相应的属性时,给出反例作为证据帮助设计者调试系统.对于系统某个属性而言,测试方法通过设计测试用例、运行系统、观察输出等环节来验证系统是否满足这个属性,但这种方法是不完备的;而模型检验方法则通过算法证明系统是否满足这个属性,针对属性而言该方法是完备和可靠的.经过许多学者的努力,该方向的研究工作取得了重要的进展.除了计算机领域的研究人员,各种系统设计者和开发者乃至整个工业界都日益重视在软硬件开发项目中应用时序逻辑模型检验方法,以提高所开发系统功能和性能方面的质量[12-16].
传统的时序逻辑,例如CTL和LTL,它们的语义模型是基于状态,例如Kripke结构[1],因此它们适合描述状态基结构的性质.在进行相应的模型检验时,不得不建立各种抽象层次的状态基模型.时序逻辑的这种语义定义方法,没有考虑系统设计和实现的结构因素.此处强调的结构因素指设计和实现的控制结构,不包括普通意义上的数据结构,例如图1所示程序中的循环结构和选择结构.但是对于开发者而言,在许多情况下,基于系统设计和实现的结构特征描述所开发系统的属性是一种更为自然直观的方式.各种集成开发环境所提供的程序点断言机制就是一种简单的基于程序结构的属性描述方法,更进一步,一些语言提供了比程序点断言更为复杂的基于结构的属性描述方法[17-19],例如Java模型语言(Java modeling language, JML)[20].JML在Java语言的基础上设计了一些特殊语言机制,可以描述循环不变式及成员方法输入和输出应该满足的条件等,但是这些方法的描述能力具有很大的局限性.对于图1所示程序,必须满足下面4个属性:1)对于任意一条执行路径,数组b所分配的内存资源一定在将来某个时刻会被回收;2)假如返回值为0,则数组a所有元素的值一定为0;3)在程序点5和程序点9之间属性i≤a.length∧spot≤a.length为真;4)在程序点5和程序点9之间,若spot≠a.length,则对于0≤i≤spot,a[i]=0.这些属性具有显著的特点:它们都与程序静态结构相关,并且包含动态行为时序性.

Fig. 1The source code of the function find.
图1函数find源代码
上面的实例说明构造基于系统设计和实现的时序逻辑系统及设计相关的模型检验算法具有很大的必要性和价值.鉴于CTL具有足够的表达能力和可判定的逻辑属性,本文提出一种区间分支时序逻辑——控制流区间时序逻辑(control flow interval temporal logic, CFITL),用于描述抽象程序模型——控制流图(control flow graph, CFG)的时序性质.该逻辑的语义解释集成了程序基于状态的执行语义及静态结构语义,可以描述基于结构和动态行为的各种时序属性,例如程序点断言及循环结构不变式属性等.本文在给出CFITL详细语法的基础上,基于CFG的一种受限子集,定义状态集的偏序集及相关的位阶函数rank,用以解释CFITL公式所涉及的结构因素,进而基于符号状态路径对CFITL完整的语义进行定义.基于可达状态空间计算的方法讨论了CFITL的模型检验问题.考虑CFITL模型检验是路径敏感的,比CTL模型检验具有更高的复杂性以及问题域的源程序在数据与操作方面的复杂性,本文基于符号执行技术[21-23]及时序逻辑公式重写技术[24]定义了CFITL公式的重写规则,提出基于可满足性模理论(satisfiability modulo theories, SMT)[25]的有界模型检验方法.详细设计了CFITL模型检验器的体系架构,实现了原型系统VerTPCFG(verifica-tion of temporal property of CFGs),实施相关的实例研究,对所提算法的有效性和效率进行初步评估.
1 控制流区间时序逻辑CFITL
控制流区间时序逻辑CFITL是计算树逻辑CTL的一种扩展,通过在语法上引进区间的概念来描述目标的结构因素.基于CFITL所描述的属性把系统基于状态的功能性属性与系统设计或实现的结构性因素相关联.本节将详细介绍该逻辑系统的语法和语义模型.
1.1语法
给定原子命题集合AP及自然数集合区间I,下面给出CFITL的抽象语法定义:
ψtrue|p|ψ|ψ1∧ψ2|ψ1∨ψ2|ψ|ψ|
上面抽象语法定义中,p∈AP;和称为路径量词,需要注意的是此处路径量词的语义与CTL中量词的语义有较大的区别,这一点将在逻辑公式的语义定义中得到说明.,,,是时序算子,分别表示“下一”、“将来”、“总是”、“直到”的时间概念. 式中true表示逻辑常量“真”,各种逻辑运算符∧,,∨符合标准的逻辑解释,包括没有明确定义的逻辑运算符→和逻辑真值false.
1.2语义
1.2.1控制流图和位阶函数
为了使得所定义的逻辑框架不与具体的程序语言相关,本节定义程序的抽象模型——控制流图,该结构将作为CFITL语义解释的基础.CFG只关注程序的控制流,忽略程序的数据流方面的特性.
定义1. CFG是多元组结构〈Σ,Start,Act,→,Final〉,其中Σ,Start,Act,→,Final分别解释如下:
1)Σ是有限的状态集合,非空集合Start⊆Σ为初始状态集合,非空集合Final⊆Σ为终止状态集合;
2)Act称为动作集合;

令集合Vars为所有程序变量的集合,v∈Vars,Dv表示变量v的取值范围,V={v1,v2,…,vn}⊆Vars,DV=Dv1×Dv2×…×Dvn.此处的状态集合Σ类似于程序计数器,不同于系统的状态空间DVars,是抽象的位置标示符集合,用来记录程序的静态结构信息.元素l∈Σ被视为字,也即字符串类型. 如果程序模块具有单入口和单出口的特性,集合Start和Final可用init∈Σ和final∈Σ代替,分别表示开始状态和结束状态.Act包含2种类型的动作:v=e和assume(c),其中e表示各种满足程序语言语义约束的运算表达式,c为不含量词的一阶逻辑公式. 需要注意的是,此处的e和c中不含各种可能引进副作用的程序表达式,例如许多程序语言允许v=++x这样的操作,如果程序出现这种操作,在构建程序相关的CFG时,应把该操作执行分解为操作x=x+1和v=x的顺序执行,并引进相应的状态标签. 符号序列l0a1l1a2…ln-1anln称为CFG的执行路径,其中∀0≤i≤n·li∈Σ,i0∈Start,∀1≤j≤n·aj∈Act, ∀0≤i≤n-1·〈li,ai+1,li+1〉∈→,此处所谓的执行路径没有要求ln∈Final,n为路径的长度. 在不需要强调动作的情况下,路径可以直接用状态序列表示,例如l0l1…ln.
基于Σ,下面给出前缀闭合字串集的概念.令Σ+表示Σ中元素构成的所有字串的集合,不包含空串.
定义2. 令ws⊆Σ+,如果对于任意str∈ws,str的任意非空串的前缀pre满足pre∈ws,则ws被称为前缀闭合字串集.
令PathG⊆Σ+为CFG G=〈Σ,Start,Act,→,Final〉的所有路径的集合,根据定义2可知PathG为前缀闭合字串集合. 对于某程序的控制流模型G,状态集合Σ是有限集合,但由于循环结构的存在,PathG可以是无限的. 路径集合PathG是根据G(程序)的静态结构所得到的,没有考虑程序的语义,因此包含程序任意可能的执行路径.程序中的任意循环结构都假定循环体能执行任意次,即使循环次数为定值的循环结构,换句话说,在计算PathG时,对循环条件不做任何解释,条件true,n≤10和x2+y3≠a4+b5在任何环境里,具有一样的效果,仅是一个未解释的循环条件.p,p′∈PathG,当p为p′的前缀时可记为pp′,显然结构〈PathG,〉为偏序集.
为了讨论问题需要,下面给出函数last和函数MinPathG的说明.函数last:PathG→Σ用于计算给定路径的终止状态,即last(l0l1…ln)=ln,last是部分函数,如果p∈PathG是无限路径,last(p)没有定义.MinPathG:Σ→(PathG)为给定状态的最短路径计算函数,(PathG)表示PathG的幂集,当状态l∈Σ和路径S⊆PathG满足以下条件1和条件2时,MinPathG(l)=S:1)对于s∈S,last(s)=l;2)对于s∈S,当s′s,last(s′)≠l.路径之间的偏序关系可扩展至路径集合的情形,给定l,l′∈Σ,MinPathG(l)MinPathG(l′)等价于∀p∈MinPathG(l)·∃p′∈MinPathG(l′)·pp′.
定义3. 〈Σ,◁〉.令G=〈Σ,Start,Act,→,Final〉,◁⊆Σ×Σ:
1) 对于任意的l1,l2∈Σ,如果MinPathG(l1)MinPathG(l2),那么l1◁l2;
2) 假如存在路径集合P=l0l1…li(li+1|ii+2|li+2|ii+3…|li+j)*li+j+1⊆PathG,并且li+j+1≠li+1,li+j+1≠li+2,…,li+j+1≠li+j,则li+1◁li+j+1,li+2◁li+j+1,…,li+j◁li+j+1.
在定义3中,P=l0l1…li(li+1|ii+2|li+2|ii+3|…|li+j)*li+j+1使用了正规式语言的描述方法,式中|和*运算代表“或”运算和“闭包”运算.根据正规式语言的解释,正规式实质上描述的是语言,即字串(路径)的集合.闭包运算用于描述程序中循环结构的控制流模型,代表循环体执行任意次,包括0次.图2(a)给出了图1所示程序的控制流模型,根据定义3可知〈{l0,l1,…,l18},◁〉是严格偏序集.实质上〈Σ,◁〉反映了相关CFG的拓扑结构所关联程序的控制结构信息及程序执行语义信息,但并不是根据任意的CFG构造出的结构〈Σ,◁〉都是完备格.图2(b)所示的CFG由于存在goto动作(goto相当于Act中的assume(true)),并进行了特殊的无条件跳转,导致该CFG相关的〈Σ,◁〉为非偏序集结构.从图2(b)可以看出,该CFG存在路径集合P1=l0l1(l2l4l5)*l8l3l6l7和P2=l0l1l3l6l9l5l4(l2l4l5)*l8l3,根据◁的定义,从P1和P2分别可以得出以下的关系式:l6▷l2,l6▷l4,l6▷l5和l6◁l2,l6◁l4,l6◁l5,显然〈Σ,◁〉不是偏序集.当然,并不是所有含有goto动作的CFG相关的〈Σ,◁〉都不是偏序集.实质上图2(a)中的assume(true)也是一种无条件转移操作,相当于goto的作用,但由于assume(true)转移的目标状态受到限制,例如仅仅限于循环的开始状态,不影响关系◁的结构.另外,结合动作assume(c),其中c不为false和true,assume(true)能实现大多数高级程序设计语言循环结构经常使用的“break”和“continue”语句的功能,根据关系的定义,CFG中这种类型的assume(true)动作不影响◁的结构.
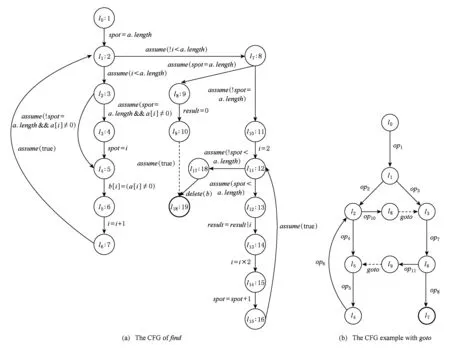
Fig. 2 The CFG examples.图2 CFG实例
从Böhm-Jacopini定理[26-27]可知,CFG能表达由顺序结构、选择结构和循环结构构成的可计算函数,并且含有“goto”语句的可计算函数可通过算法等价转换为不含“goto”、由3种结构构成的函数.根据程序语言理论,对于描述程序的CFG,当assume(true)∈Act的作用仅限于循环结构的无条件转换、“break”和“continue”时,如果l,l′∈Σ满足l◁…◁l′,则l′◁…◁l.本文把描述不含有“goto”语句的程序的CFG称为受限CFG,后文没有特别说明,所涉及的CFG都局限于这种类型.
定理1. G=〈Σ,init,Act,→,final〉为不含“goto”语句的可计算函数构造的CFG,〈Σ,◁〉为严格偏序结构.
证明. 该定理的证明可基于程序的静态结构进行归纳证明,下面对证明过程做出详细的说明.可计算函数由顺序结构、选择结构和循环结构组成,这些结构从单纯的基础结构,通过嵌套构成任意复杂的结构.这3种结构分别用seq,branch,loop表示,不同的同种结构可用下标进行区分,seq(str1,str2,…,strn) 表示由结构str1,str2,…,strn顺序组成的顺序结构,branch(c,str1,str2)是选择条件为c且真分支和假分支结构分别为str1和str2的选择结构,branch(c,str)表示只有真分支的选择结构,loop(c,str)是循环条件为c、循环体为str的循环结构,显然,可计算函数也可表示为多层嵌套的3种结构之一.因此只要说明每种结构所涉及的状态集与关系◁构成偏序集即可.令Σ[str]表示结构str所涉及的状态集,根据程序语言理论,当str1和str2没有嵌套关系时,Σ[str1]∩Σ[str2]=∅.
1) 基础步.当str,str1,str2为基本顺序结构时,branch(c,str1,str2)和loop(c,str)分别为基本选择结构和基本循环结构. 显然〈Σ[str],◁〉为线性偏序集,〈{lc}∪Σ[str1],◁〉,〈{lc}∪Σ[str2],◁〉,〈{lc}∪Σ[str],◁〉分别为线偏序集,因此〈{lc}∪Σ[str1]∪Σ[str2],◁〉为偏序集,即〈Σ[branch(c,str1,str2)],◁〉为偏序集.并且这些偏序集都存在最小元素,结构str如果存在最小元素,则记为min(str).lc为选择或循环结构的入口状态.
2) 假设步和归纳步.假设〈Σ[str1],◁〉,〈Σ[str2], ◁〉,…,〈Σ[strn],◁〉都为偏序集,且str1,str2, …,strn都存在最小元素.下面说明〈Σ[seq(str1,str2,…,strn)], ◁〉为偏序集.根据顺序结构的构造原理,对于1≤i≤n-1,任意l∈Σ[stri],l◁min(stri+1),所有〈Σ[stri]∪Σ[stri+1],◁〉为偏序集,且有最小元min(stri).因此〈Σ[str1]∪Σ[str2]∪…∪Σ[strn],◁〉为偏序集,最小元为min(str1),即〈Σ[seq(str1,str2,…,strn)],◁〉为偏序集,且min(seq(str1,str2,…,strn))=min(str1).采用类似的方法,容易证明〈Σ[branch(c,str1,str2)],◁〉和〈Σ[loop(c,str1)],◁〉分别为偏序集并且存在最小元lc.
证毕.
定义4. 令G=〈Σ,init,Act,→,final〉,〈Σ,◁〉是偏序集,函数rankG:Σ→满足以下性质时,称为CFG G的位阶函数:
1) 对于任意的l1,l2∈Σ,如果l1◁l2,rankG(l1) 2)rankG是一一映射函数,即对于任意l≠l′,rankG(l)≠rankG(l′). 图2(a)所示的CFG相关的位阶函数rankG(li)=i+1,其中0≤i≤18,状态值及相应位阶函数值标记在相应的状态里.位阶函数作为一种特殊的函数,把程序的控制结构信息及程序执行语义信息与自然数集进行关联,用于解释CFITL公式的区间信息.位阶函数是由〈Σ,◁〉诱导的,且映射结果在<上保序,如果CFG相关的〈Σ,◁〉不为偏序集,这意味着该CFG不能定义相应的位阶函数;但如果位阶函数存在的话,则位阶函数不是唯一的.例如:任意n≥1,rankG(li)=n×(i+1)都是图2(a)所示CFG的位阶函数.图2(b)所示的CFG由于存在goto动作,进行了特殊的无条件跳转,导致该CFG的拓扑结构没有相应的位阶函数. 1.2.2CFITL的解释模型 其中,s[op]表示符号状态s执行动作op∈Act的后继状态,[c]s表示基于符号状态s评估条件c的真假值,A[v←e]表示A′:Vars→Terms,对于v′∈Vars:当v′≠v,A′(v′)=A(v′);当v′=v,A′(v′)=[e]s,[e]s与[c]s类似,表示在符号状态s评估表达式e的值.对于符号状态s,如果Π是不可满足的,则表示s是不可达的,即程序的静态结构中存在死代码. 根据符号状态的变迁关系,执行路径p=l0l1…∈PathG可用符号状态路径s0s1…表示.其中s0=〈l0,A0,Π0〉为初始符号状态,A0用符号变量或常量初值对所有的程序变量进行初始化;Π0则记录程序变量之间的约束关系,假如程序变量之间没有任何约束,Π0=true.如果s0是唯一的,每条路径p∈PathG对于唯一的符号状态路径.对于i≥0,〈li,op,li+1〉∈→,si+1=si[op].为了表达方便,令SP(p)为执行路径所对应的符号状态路径,SG为G相关的符号状态集合;Loc(s)=l,Eval(s)=A,Cond(s)=Π,其中s=〈l,A,Π〉.如果对出现在符号状态中的符号变量用相应类型的常量进行代换得到DVars类型的程序变量值状态及相应的值状态变迁路径.令SV(s)表示出现在符号状态s里的符号变量,DSV(s)同DVars意义类似,表示符号变量值域的笛卡儿积,E(s)=SV(s)→DSV(s)为对符号变量进行常量赋值的映射集合,被称为符号状态s的环境.一般情况下,集合Act中的动作不会引进新的符号变量,因此任何符号状态路径中的符号变量集合为SV(s0),所有符号状态s的环境满足E(s)⊆E(s0).对任意环境E,记E(Π)={A∈E|E(E0(Cond(s))∧Loc(s)=l),其中E0=E(s0),l∈Σ,s∈SG. 定义5. 给定CFG G=〈Σ,init,Act,→,final〉和rankG,二元组M=〈G,rankG〉称为含序CFG结构. 下面基于含序CFG结构M及符号状态路径建立区间时序逻辑CFITL的解释模型.(M,l0)Eψ表示在环境E下结构M的状态l0满足公式ψ,具体定义如下: (M,l0)Etrue iff E≠∅. (M,l0)Epiff ∀s=〈l0,A0,Π0〉∈SG·∀A∈E(Π0)·A0∧Ap. (M,l0)Eψ1∧ψ2iff (M,l0)Eψ1and (M,l0)Eψ2. (M,l0)Eψ1∨ψ2iff ∀s=〈l0,A0,Π0〉∈SG·∀A∈E·((M,l0){A}ψ1∨(M,l0){A}ψ2). (M,l0)Eψiff (M,l0)Eψ. (M,l0)Eψiff ∃P=l0l1…∈PathG·(SP(P)=s0s1…∧(M,l1)E (Cond(s1))ψ). (M,l0)Eψiff ∀P=l0l1…∈PathG·(SP(P)=s0s1…∧(M,l1)E (Cond(s1))ψ). (M,l0)Eψiff ∃P=l0l1…l∞∈PathG·(SP(P)=s0s1…∧∀i≥0·(M,Loc(si))E (Cond(si))ψ). (M,l0)Eψiff ∀P=l0l1…l∞∈PathG·(SP(P)=s0s1…∧∀i≥0·(M,Loc(si))E (Cond(si))ψ). (M,l0)Eψiff ∃P=l0l1…∈PathG·(SP(P)=s0s1…∧∃i≥0·(M,Loc(si))E (Cond(si))ψ). (M,l0)Eψiff ∀P=l0l1…∈PathG·(SP(P)=s0s1…∧∃i≥0·(M,Loc(si))E (Cond(si))ψ). (M,l0)E(ψ1ψ2) iff ∃P=l0l1…∈PathG·(SP(P)=s0s1…∧∃j≥0·(∀0≤i (M,l0)E(ψ1ψ2) iff ∀P=l0l1…∈PathG·(SP(P)=s0s1…∧∃j≥0·(∀0≤i (M,l0)EIψiff ∃P=l0l1…∈PathG·(SP(P)=s0s1…∧∃i≥0·(rankG(li)∈I∧(M,li) (M,l0)EIψiff ∀=l0l1…∈PathG·(SP(P)=s0s1…∧∃i≥0·(rankG(li)∈I∧(M,li) (M,l0)EIψiff ∃P=l0l1…l∞∈PathG·(SP(P)=s0s1…∧∀i≥0·(rankG(li)∈I∧(M,li) (M,l0)EIψiff ∀P=l0l1…l∞∈PathG·(SP(P)=s0s1…∧∀i≥0·(rankG(li)∈I→(M,li) (M,l0)E(ψ1Iψ2) iff ∃P=l0l1…∈PathG·(SP(P)=s0s1…∧∃j≥0·(rankG(lj)∈I∧(M,lj) (M,l0)E(ψ1Iψ2) iff ∀P=l0l1…∈PathG·(SP(P)=s0s1…∧∃j≥0·(rankG(lj)∈I∧(M,lj) 关于CFITL语义模型的解释,做出如下进一步的4点说明: 1) 语义定义中p∈AP,P=l0l1…l∞表示2种类型的路径:无限路径或满足l∞=final的有限路径.当P为无限路径时,l∞不表示具体的状态,只是表达无限的概念.标准的CTL语义解释是基于无限路径的,路径只与系统的动态行为相关;CFITL的语义解释是基于符号状态路径,既可能为无限路径,也可能为有限路径,并且符号状态路径集成了系统动态行为信息及程序静态结构信息. 2) 当环境E=∅,对于任意ψ,(M,l)Eψ.当l0=init时,(M,l0)Eψ可简写为(M,l0)ψ,此时环境为初始环境,即E(s0);当l0≠init时,由于从初始状态init开始,可能存在多条路径到达l0,根据定义5可知,每条路径可以产生环境映射,因此(M,l0)ψ意味着对于所有可能的环境E而言,(M,l0)Eψ成立.利用当E=∅,(M,l)E true的性质,可通过检验(M,init)true是否成立来判断程序是否存在死代码.当该属性不成立,说明存在死代码. 3) 由于CFITL的语义模型与CTL语义模型有着根本的差异,因此一些在CTL里很自然的、符合直觉的逻辑关系在CFITL里不一定成立,例如ψ≢ψ,ψ≢ψ,如果(M,l0)Eψ1∨ψ2并不等价于(M,l1)Eψ1∨(M,l0)Eψ2等. 4) 集合Act含有2种类型的动作:赋值动作v=e和条件判定动作assume(c).在程序语言层面,赋值动作改变程序变量的值,程序的执行语义模型的状态迁移描述了这种迁移前后状态之间的关系;条件判定动作不会改变程序变量的值,一般隐式或显式地作为前一种动作的约束条件体现在程序的语义模型的状态变迁中.用于解释CFITL公式中时序算子的路径l0l1…包含2种操作所导致的CFG结构中的状态变迁,这种时序的观念集成了程序静态结构的“序”概念和体现程序动态行为的程序变量值状态变化的“序”概念,这一点与CTL公式时序算子的“序”的解释不一样.当然,通过简单的转换,可以去掉路径l0l1…中操作assume(c)所导致的状态变迁,建立起与CTL标准解释模型Kripke结构一致的“序”的观念. 按照CFITL公式的语义解释,下面分别用CFITL公式描述图1所示程序应该满足的4条典型性质: 以上的公式中,delete(b)表示命题“数组b所占用的内存空间被释放”,Zero(a)表示命题“数组a所有的元素值为0”,Zero(a,0,spot)表示命题“数组a从第1个元素至第spot个元素的值为0”.性质2中2个公式等价,描述的是同一性质,19是[19,19]的简写.根据公式的语义解释可知,图1所示程序满足性质2~4,不满足性质1. 1.2.1节论及对于给定的CFGG,如果存在位阶函数,则存在无穷个满足定义4的位阶函数.这意味着同一描述程序结构特征和动态行为特征的CFITL公式可以构造不同的含序CFG结构〈G,rankG〉,对公式给出不同的解释.为了消除CFITL公式相对于CFG所呈现的多义性,下面提出规范化位阶函数的概念.正如定理1的证明所述,一个可计算函数(程序)是由顺序结构、选择结构及循环结构3种类型的程序块通过嵌套的方式所产生,并且程序本身也属于这3种结构之一.为了表述方便,引进表达式P[str1,str2,…,strn],其中P,str1,str2,…,strn是seq,branch或loop类型的结构.P[str1,str2,…,strn]结构表示程序P包含n个各种结构的程序块str1,str2,…,strn,表达式中的逗号“,”与seq(str1,str2,…,strn)或branch(c,str1,str2)中的逗号不一样,没有“序”的概念.任意2个不同的程序块Bi和Bj可以是嵌套关系或非嵌套关系.G=〈Σ,init,Act,final,→〉为与P相关的CFG;rankG为G的某个位阶函数,如果rankG满足下列4个条件,则被称为规范化位阶函数(规范化位阶函数记为nrankG): 1) 对于任意l∈Σ,1≤rankG(l)≤|Σ|,即函数rankG为类型Σ→[1,|Σ|]的双射函数. 2) 对于P的任意程序块Bi,当l∈Σ[stri],rankG(l)∈[low,high],对于任意n∈[low,high],存在l∈Σ[stri],rankG(l)=n.显然1≤low≤high≤|Σ|.满足此条件的位阶函数确保属于同一程序块的状态集合所对应的序数集合为某一完整的自然数区间. 3) 当stri为选择结构程序块,strt和strf分别为“真”分支程序块和“假”分支程序块,则对于任意l∈Σ[strt],l′∈Σ[strf],rankG(l) 4) 对于任意基本程序块stri和strj,如果它们之间没有嵌套关系,并且rankG(Σ[stri])=[low1,high2],rankG(Σ[strj])=[low2,high2],则[low1,high1]∩[low2,high2]=∅,如果stri嵌套于strj,则Σ[stri]⊆Σ[strj],式中rankG(Σ[str])={n∈|n=rankG(l),l∈Σ[str]},str为任意结构的程序块. 对于给定的CFG G,如果〈Σ,◁〉是偏序集,则存在位阶函数rankG及相应的规范化位阶函数nrankG,且该规范化位阶函数是唯一的.定理2给出了规范化位阶函数存在性和唯一性的证明.如果用含序CFG结构〈G,nrankG〉代替普通的含序CFG结构〈G,rankG〉,则CFITL公式的解释具有唯一性.下文如果没有特别说明,CFITL公式的解释都是基于规范化位阶函数. 给定程序P、该程序诱导的偏序集〈Σ,◁〉、规范化位阶函数nrankG、程序P所包含的结构str,并且任意l∈Σ[str],nrankG(l)∈[low,high]. 结论1. 当str为顺序结构seq(str1,str2,…,strn),根据规范化位阶函数的定义可得以下性质: 2) 对于任意1≤i 结论2. 当str为选择结构branch(c,strt,strf),同理可得以下性质: 1) |Σ[str]|=|Σ[strt]|+|Σ[strf]|+2=high-low+1,式中的2表示选择结构的开始状态和结束状态; 2)nrankG(lc)=low,nrankG(lend)=high,lc和lend分别为开始状态和结束状态; 3) 任意l∈Σ[strt],nrankG∈[low+1,low+|Σ[strt]|],l∈Σ[strf],nrankG(l)∈[low+Σ[strt]+1,high-1].当str为只有真分支的选择结构branch(c,strt)时,|Σ[str]|=|Σ[strt]|+1=high-low+1,任意l∈Σ[strt],nrankG(l)∈[low+1,high],nrankG(lc)=loc. 结论3. 当str为循环结构loop(c,str),根据关系◁的定义可知,循环结构中具有无条件转移作用,但转移目标状态受限的动作assume(c)对构造◁的拓扑结构没有实质性的影响,因此对于循环结构loop(c,str)和选择结构loop(c,str)而言,规范化位阶函数nrankG在状态集合Σ[loop(c,str)]上的性质是等价的. 定理2. 对于CFG G=〈Σ,init,Act,final,→〉,如果〈Σ,◁〉为偏序结构,则G存在规范化位阶函数nrankG,且是唯一的. 证明. 如果〈Σ,◁〉是偏序结构,G显然存在位阶函数.令P为与G相关的程序,不失一般性,设其结构为seq(str1,str2,…,strn),其中stri为顺序结构、选择结构或循环结构,1≤i≤n.下面通过一个构造性算法证明规范化位阶函数的存在性和唯一性. G的位阶函数rankG按以下2个步骤进行构造: 2) 假如Str_Vector≠∅,从集合Str_Vector中选择结构str(Str_Vector=Str_Vector{str}): ① 假如str为不含有选择或循环结构的顺序结构,则l∈Σ[str],nrankG(l)∈Istr,且在区间Istr,rankG具有保序的性质,Istr是结构所属的区间信息; ② 假如str为含有嵌套结构的顺序结构、选择结构或循环结构,则按照结论1~3的方法,把相关的内嵌结构加入str_Vector,并设置相关结构所属的区间,并返回步骤①. 显然按照以上步骤构造的rankG符合规范化位阶函数的性质要求,并且交换任意2个互相不嵌套结构的区间,不满足规范化位阶函数的要求,即规范化位阶函数是唯一的. 证毕. 2.1基于显式状态枚举的CFITL模型检验 第1节通过环境、符号状态及符号状态路径对CFITL公式的语义进行了详细的定义,在此基础上,本节重点讨论基于CFITL的模型检验方法.模型检验的研究始于20世纪80年代[5],主要用于验证有限状态系统是否满足一些特定的性质.基本思想是:用迁移系统表示系统的行为,用模态时序逻辑公式描述系统的性质,系统是否满足某个性质就转化为“迁移系统是否是相应的模态逻辑公式的模型”这样的数学问题.模型检验的核心问题是设计可行的算法,自动化检验迁移系统是否是相应的模态逻辑公式的模型.根据模态逻辑公式类型和表达能力以及不同的算法原理,可以构造各种不同类型的算法用于完成模型检验问题的求解.尽管这些算法类型各异,但根本上它们在执行同一任务:可达状态空间的计算. DnrankG×DVars·(∃t=〈l,op,l′〉∈→· 算法1. 模型检验算法CheckEG(f). 输入:公式f、程序P; 输出:可达状态集合S. ④S=SSCC; ⑤ while (SSCC≠∅) do ⑦SSCC=SSCC 算法2. 模型检验算法CheckEU(I,f1,f2). 输入:公式f1、公式f2、区间I; 输出:可达状态集合S. ②S=S; ③ while (S≠∅) do ⑤S=S ⑨ end while 算法3. 路径测试函数TestSymPath(S,sp). 输入:S,sp; ① if (sp=l0l1…ln为符号化路径,ln为终止状态) ②SymS={si‖0≤i≤n,SP(sp)=s0s1…sn}; ③ while (SymS≠∅) ④chooses=〈l,A,Π〉∈SymS; ⑤SymS=SymS{s}; ∃A∈E(s)·(val=A[A])}; ⑧ end while ⑨ return success; 函数TestSymPath中参数S表示值状态集合,例如算法1中的S,sp为待测试符号路径,可以采用正规语言的方式表达.参数kmax是与SCC相关的一个参数,是反映SCC路径模式的一个参数,需要计算值状态路径与正规式表达的符号路径模式匹配问题,需要很大的计算开销. 如果在系统的有界模型检验中存在阈值,则可取阈值作为kmax的保守值.当状态空间规模较小时,可采用模拟执行计算符号路径sp值状态集合不动点的方法进行计算. 下面通过与CTL的对比讨论CFITL模型检验的算法复杂度.当语义模型Kripke结构〈S,R,L〉的状态集S为有限时,CTL公式可满足性是可判定的,算法复杂度为O(len(f)(Card(S)+Card(R))).当系统实现的模型CFG所诱导的Kripke结构为有限结构时,由于刻画有序CFG拓扑结构的数值特征为整数区间,状态的数值属性为单点型的区间,在此条件下,CFITL公式可满足性是可判定的.本节基于扩展后的状态空间DnrankG×DVars构造了部分公式的判定算法,算法的复杂度为O(len(f)(Card(DnrankG×DVars)+Card(R))). CFITL模型检验算法的复杂度较CTL模型检验算法高,但并不是指数级的升高,受DnrankG约束.对于大状态空间或无限状态空间系统的模型检验,传统的基于抽象技术,例如谓词抽象,经过重新设计后仍然可以应用于CFITL模型检验,以缓解状态空间爆炸问题;另外2.2节结合CFITL公式重写技术的有界模型检验也是一种实施途径,这也是原型系统采用的基本方法. 2.2基于SMT的CFITL有界模型检验 基于状态枚举的模型检验算法一个首要的前提是构建系统的有限状态系统,例如算法1和算法2都只能应用于有限状态系统.现实中的各种类型程序涉及复杂的逻辑控制及具有无限值域的抽象数据类型,不能直接获得有限状态的系统结构,即使应用各种类型的抽象建模技术[28-29],但由于难以建立统一的、自动化的抽象机制及抽象精化方法,各种抽象技术也只能缓解,而不能从根本上克服各种模型检验方法所面临的可控规模状态空间的系统模型的构建问题,包括符号模型检验方法.另一方面,模型检验方法的完备性是相对于系统规约而言的,但开发人员不可能给出完全正确且完备的系统规约,以确保所开发的目标系统是完全“正确”的系统,而且,在资源受限的情况下,再先进的模型检验器也不可能对系统所有的属性进行验证. 基于以上这些因素,Clarke等人提出有界模型检验的思想[9],这种方法不要求验证具有完备性,并且把基于可达状态集合的计算问题转化为命题逻辑的可满足性判定问题.这样,模型检验问题可以利用许多高效的可满足性判定器求解,例如GRASP,SATO,ZCHAFF等[30-31],从而避免可达状态集计算所带来的存储空间和计算时间的开销问题.从某种意义上,可以认为有界模型检验方法是介于测试和一般模型检验之间的一种方法,它采用定理证明的方法测试在系统的局部行为空间内规约是否成立,兼具测试和证明的特点,因此有界模型检验除了用于证明属性是否成立外,还经常用于查找程序的错误. 从上面的论述可以看出,有界模型检验方法的性能和能力取决于可满足性判定器.由于现代程序含有各种复杂的抽象数据类型及操作,包括GRASP和SATO等传统的命题逻辑可满足性判定器难以直接应用于程序属性验证.近年来,可满足性模理论及相关工具得到了快速地发展,例如:Z3[32],CVC,MathSAT等.SMT问题是命题逻辑公式可满足性判定问题的扩展:谓词逻辑公式的可满足性判定[25].纯逻辑领域不涉及任何领域性的理论,但在实际的应用中,大部分SMT判定器都内建有复杂的领域理论,包括整数理论、实数理论、未解释函数理论及一些处理复杂数据类型的理论,如向量、队列和数组理论等. 这些背景理论的集成使得SMT判定器具有描述及推理复杂的特定领域问题的能力.许多程序分析与验证领域的问题:可验证的编译方法、谓词抽象、模型检验等,这些问题都可转化为SMT问题,利用集成多种不同背景理论的SMT判定器进行求解.SMT研究领域的众多的研究机构和研究人员提出了SMT工具的标准通讯语言和命令,被称为SMT-LIB,通过SMT-LIB可以方便地描述背景理论、各种复杂的待求解的问题及操纵各种SMT工具,并且这些SMT工具大都提供了丰富的人机接口和编程接口. 基于SMT的CFITL模型检验方法的关键环节是把有界模型检验问题归结于SMT,用集成了各种域理论的谓词逻辑语言进行描述.给定含序CFG结构M=〈G,nrankG〉,待验证时序属性f及界限K(K≥0),用[M,f]K表示长度为K的符号状态路径满足f的充分必要条件, [M,f]K由2部分组成:1)长度为K的来自CFG G的符号状态路径的行为及静态结构规范,记为[M]K;2)满足属性f且长度为K的路径应该满足的条件,记为[f]K,[M,f]K=[M]K∧[f]K. 由于符号状态路径s0s1…的最大长度为K,因此上式中i≤K-1,[p]si表示基于符号状态si对命题p进行解释.根据语义定义可知,析取运算∨的行为不具有一般意义上的那种直觉的性质,即(M,l)Eψ1∨ψ2等价于(M,l)Eψ1∨(M,l)Eψ2,上式中关于析取运算给出了一种更强的重写结果,如果要得到等价SMT的编码形式,则需要引入量词.关于时序算子的重写规则需要特别的进一步的解释.根据定义5可知,I和语义解释涉及2种类型的符号状态路径:一种是无限路径;一种是有限长度路径,且当程序执行完该路径后处于终止状态.当sK满足Loc(sK)=final,且不存在op∈Act,l∈Σ,〈Loc(sK),op,l〉∈→时,即s0s1…sK是程序的一条完整的执行路径,则只要迭代应用公式重写规则计算出[和.当s0s1…sK不是程序的完整路径,即Loc(sK)≠final,或者当Loc(sK)=final,存在op∈Act,l∈Σ,〈Loc(sK),op,l〉∈→,那么可以分成以下2种情况: 1) 当该路径为套索路径(lasso-shape path)[33]时,有限路径展现出无限路径的性质,该有限路径满足[或意味着相关的无限路径满足ψ或Iψ.当存在0≤i≤K,并且存在op∈Act,〈Loc(sK),op,Loc(si)〉∈→,对于所有的A∈E(sK),Eval(si)=Eval(sK)[op],s0s1…si…sK为套索符号路径,与其相关的无限路径为sos1…(si…sK)ω,其中ω表示无限的意思. 上式中Δ表示任意的路径量词.需要强调的是上面所讨论的在有界模型检验的条件下证明ψ和Iψ的方法可靠但并不完备,因为当程序所实现的系统为无限状态系统时,存在不含套索的无限路径满足ψ或Iψ.以一个没有上界的简单计数器为例,该系统是无限状态系统,显然容易得到一个不存在套索路径且满足(count≥0)的系统实现,count为计数器变量.如果结合符号状态路径的结构特性和时序算子的语义特性,同样可以得出一些关于[和的更有意义的结论.例如:如果有界符号路径s0s1…sK不满足[ψ]K或[Iψ]K,并不能得出没有以s0s1…sK为前缀的路径满足[ψ]K或[Iψ]K,但如果s0s1…sK满足IE,则可以据此得到可靠且完备的结论,即s0s1…sKΔIψ⟺s0s1…sK…ΔIψ. 从上面的相关分析可以看出,虽然有界模型检验方法不是完备的,但结合模型结构的分析,可以得到可靠且完备的结果,这方面的工作可参考文献[9]. 实际上,在实施模型检验时,根据不同类型的属性f,可以采用不同的验证策略.例如对于安全性属性(p1∧p2),可以通过验证是否满足((p1∧p2))的结果考察属性(p1∧p2).假如满足((p1∧p2)),则(p1∧p2)不成立,并且满足((p1∧p2))的符号状态路径是反例,进一步调用SMT工具获得值状态路径,结合2种类型的路径信息,可以更精确地对程序进行调试,定位程序错误;当在界限为K的条件下,((p1∧p2))不成立,则进一步根据系统的结构特性,例如完备的界限阈值及相关的路径特征属性信息LC,TC,IE等作出判断,决定下一步采取的策略.对于形如p的活性属性同样可以采取2种验证策略. CFITL直接用于描述程序的各类与静态结构及动态行为相关的时序属性,为了使所设计的模型检验器系统开发成本尽可能低、运行自动化程度尽可能高、能处理的程序数据类型和结构尽可能丰富,尽量复用已有的高性能的开源软件工具,基于SMT的有界模型检验方法实现了相关的原型工具. CFITL有界模型检验器总体架构如图3所示: Fig. 3 The framework of bounded model checker over CFITL.图3 CFITL有界模型检验器框架 Fig. 4 The prototype system of VerTPCFG.图4 VerTPCFG原型系统平台 图3所给模型检验器设计框架中的大部分内容在第2节都有所涉及,下面就图中标有★的部分内容作进一步的介绍.为了增强验证工具的可扩展性,在程序和CFG之间设计了一个中间语言层,使得CFG独立于具体的程序设计语言.具体的程序至中间语言的翻译由预处理过程“preprocess”负责处理,不同的程序语言对应不同的预处理过程.当然,为了得到有序的CFG结构,预处理过程还需要对原程序的语法进行有效性检查及程序的等价转换,这方面的主要内容包括有副作用语句的等价变换和有害“goto”语句的消除.中间语言采用STG Format[34],这种语言由IF规约语言子集改编而成,用于描述各种复杂的顺序及并发反应式系统.目标系统的程序设计与实现是一种具有创新性的工作,深刻地体现开发人员的主观能动性,对于同样的功能需求,具有不同知识背景和思维能力的人所设计程序的静态语法结构差异极大,单条语句语法与语义可能存在极大的差别.面临这种情况,在构造CFITL的语义模型有序CFG结构时有2种处理策略:1)允许动作集合Act的元素具有“副作用”,与源程序的语句保持一致,这样使得CFG基本结构与源程序具有相同的静态语法结构;2)限制集合Act元素的复杂性,使得它在语法层面上具有“原子性”,这样CFG静态结构与源程序的静态结构会存在某种程度的不一致性. 第1种处理方法的优点是开发人员可以依据自己的程序实现写出要求满足的属性公式,但这种方法有着显而易见的缺点,即系统的动态行为(状态空间及状态变迁关系)与语句形态高度耦合,CFITL的“时序”的意义没有统一的解释;第2种方法保持了对动态行为模型的认识观点,使得CFITL的“时序”具有统一的解释,即一个在语法层面上不具有副作用的原子语句的执行就意味着系统变换至下一时刻点.但第2种方法也有不足,由于程序与相关的CFG在结构上存在不一致的地方,因此在描述涉及与结构相关的属性时,需要利用“compute_nrank”处理过程输出有序CFG结构的详细信息.图3所示的方法采用一种折中的方法,即CFG的构建按照第2种处理策略,但属性描述所涉及的结构因素(区间)按照源程序的结构特征进行解释.这种处理方法的优点是属性的描述不需要完整的CFG信息,属性的结构要素与源程序保持一致,最符合开发人员的直觉认知.这会产生一个关键性的问题需要处理:建立虚拟CFG(Act集合与源程序的语句保持一致)与CFITL有序CFG结构之间的结构映射关系,这是过程“Interval_map”的核心工作.输入“Verifying Strategy”代表2.2节的验证策略.给定一个待验证的属性,可以根据公式的类型和特点及界限参数K,选择“证明驱动”策略或“反例驱动”策略,不同的策略意味着不同的〖f〗K输出. 基于图3的系统架构,设计了VerTPCFG原型系统,图4显示了该原型系统.目前,该系统还缺乏真正的前端,仅实现了基于STG Format语言的系统规约及其静态结构和动态行为属性的分析和验证.基于原型工具VerTPCFG,选取汽车风挡刮水控制器(windscreen wiper controller)、饮料销售自动机(beverage machiner)和电梯控制器(elevator controller)作为基本实验对象,这些实验对象用STG Format语言进行描述.每个实验对象各设计了4条属性,这些属性基本都含有静态结构因素,例如循环不变式属性,界限的值简单地根据由系统描述所产生的CFG中最长路径长度确定,实验中人为确定为路径长度的3倍.这些属性大都是安全性属性,因此除明确给出了反例的属性外,大部分属性的验证结果是不完备,原型工具没有计算LC,TC,IE.实验结果表明各条属性都在30 s以内得到证明,当然这与所给的属性公式的文本复杂度较低,不涉及复杂的时序算子的嵌套及K的取值相对较低等多种因素相关.通过观察验证过程,发现较多亟待解决的问题,例如:验证[t1,t2]ψ类的属性时,容易给出平凡的路径,例如该路径所有状态的位阶不属于区间[t1,t2];验证[t1,t2]ψ类属性时会出现大量无意义的路径信息的计算.由于原型系统没有实现复杂数据类型的处理,且缺乏完整前端处理过程,即实现有效的程序实现语言到中间语言的翻译,因此仅选取了几个偏于控制类型的简单例子. 时序逻辑和基于时序逻辑的软硬件系统的时序属性规约及验证是形式化方法领域的重要研究内容,鉴于CTL和LTL在表达能力、语法的易用性和判定算法的效率等方面所具有的平衡性,与之相关的逻辑理论、判定算法和数据结构及工具软件的开发和应用等方面的研究工作已经取得丰富的成果,并且这些成果已经成功地服务于工业界[1-2,5,8-12].国内唐稚松院士较早开展了关于时序逻辑理论方面的研究工作,提出了XYZE时序逻辑系统,该逻辑系统包括2个语言子集 XYZAE和XYZEE,分别用于描述程序的静态语义和动态行为语义的属性规约[35-36]. CTL和LTL等这些时序逻辑仅能用于描述系统的动态语义属性.显然,系统的动态行为属性由程序实现的静态结构属性决定,直接对实现的结构语义属性进行规约和推理具有重要的意义,是确保系统动态行为属性正确性的基础.近年有多种逻辑被提出,用于处理程序实现的各种重要语法要素,例如指针和数组等,典型的包括分离逻辑[37]、范围逻辑[38]和动态逻辑[39]等.分离逻辑和范围逻辑用于含有指针程序的属性分析;而动态逻辑则引入了类似于时序算子的模态算子,用于规约和推理程序的动态行为属性.另外,陈意云教授研究团队提出了指针逻辑和形态图逻辑系统[40-41]用于对指针及递归数据结构的性质进行分析. 相比上面所提及的几类逻辑系统,CFITL具有显著的特点和优势.类似于CTL和LTL的时序逻辑系统,只具有规约和推理系统动态执行语义属性的能力,而缺乏规约系统实现的静态结构语义.CFITL则具备在统一的框架内规约和推理静态结构语义和动态行为语义属性的能力.CFITL的语法定义是基于CTL扩充而来的,但语义定义具有很大的差异,两者的表达能力具有相关性,又有很大的差异性.例如对于只含有全称路径量词的CTL属性,在CFITL逻辑框架内能进行等价地表达;对于含有路径量词的公式,没有或不易构造相应的CFITL等价式,但CFITL有相应的一种更强的表达,即对于CTL公式fctl、CFITL公式fcfitl,如果(M,l0)fcfitl,则(K,s0)fctl,其中K为系统实现M所诱导的Kripke结构,fctl和fcfitl语法具有一定关联性.当然,即使把这种更强的关系视为等价关系,也并不意味着CFITL语言包含CTL.显然,由于CFITL引进了区间的概念,关于静态结构属性的CFITL大部分描述在CTL框架里显然不能等价地表达.当然CTL和CFITL语义解释之间的关系,下一步的工作将进行更加细致的研究. 分离逻辑和范围逻辑这类型的逻辑是Hoare-Floyd公理系统的扩展,用于推理具有指针类行为程序的属性,由于构造系统的目的与CFITL不一致,它们不具备系统化描述动态时序属性和静态结构属性的能力.XYZE系统和动态逻辑系统可以直接用于规约和推理程序的行为属性,并且定义了类似的时序算子.相对CFITL而言,XYZE和动态逻辑系统具有较为复杂的语法体系,尤其是XYZE系统,它包含2个语言子系统,且定义了各种不同的原语,用于表达各种复杂时序属性所需要的时序、逻辑及程序结构相关的概念,动态逻辑系统基本不具备描述静态结构属性的能力;CFITL通过引进整数区间作为程序结构因素的映射,使之具备对程序各种简单和复杂的结构属性进行规约的表达能力;另外CFITL通过继承CTL的语法和语义框架,使得许多CTL模型检验方法理论和算法思想可应用于CFITL模型检验领域. 区间时序逻辑包括一类具有数量约束指标范畴的时序逻辑,这些各种不同形式的数量指标大都用于复杂系统的性能属性,例如概率约束指标、数值奖赏指标、连续或离散时间约束指标和时钟约束等,这方面详情请参阅有关文献[3,7,14,18,42-44].这些各种不同类型具有数量约束指标的时序逻辑的目标显然还是系统的动态语义范畴,与CFITL的作用有着根本的差别.另外还有一类典型的区间时序逻辑,例如PITL[45]、Halpern-Shoham逻辑[46](简称HS逻辑)及国内段振华教授提出的PTL[47],它们的语义解释是线性离散时间结构,用于规约和推理具有离散时间刻度并发系统的离散时间相关的各类行为属性.基于PITL,PTL通过引进投影和投影星操作,使之具备规约和推理并发系统时间区间上的重复性属性,甚至类似于公正性要求的无穷次重复的属性以及进程同步性属性,文献[48]进一步把PTL用于单调速率调度算法可调度性的验证.基于不同的动机所构造的CFITL,其语义解释是基于分支时间观念的非线性结构有序CFG,并且有序CFG结构作为系统实现模型,决定了系统的行为模型——Kripke结构的拓扑,因此CFITL公式集成了系统实现的静态结构语义和动态行为语义.计算机系统开发人员更习惯从系统实现的视面理解系统和规约系统,传统上经常采用谓词逻辑对系统实现进行规约,进而基于规则系统进行形式化的推理,而通过CFITL则可以采用自动的算法方法对实现的各类属性进行验证,例如循环不变式;另外,通过区间,CFITL可以对系统实现结构在各种粒度上进行规约和推理. 系统的动态行为属性由系统实现的静态结构属性决定,研究关联系统实现静态结构和动态行为属性的规约形式和分析验证方法具有重要的应用价值.本文基于CTL构建了一种区间时序逻辑系统CFITL,该逻辑系统具有描述复杂的程序静态结构和动态行为属性的表达能力,通过一类受限的CFG及CFG诱导的位阶函数给出了CFITL语义.位阶函数用于解释CFG的状态的拓扑信息,即程序的静态结构信息,定理1和定理2显示它的构造不单纯由程序的抽象视图CFG决定,还取决于CFG结构相关的程序结构因素.进一步,本文详细讨论了CFITL的模型检测问题,提出了具体的模型检测算法,包括基于可达值状态空间计算的模型检验算法和基于SMT及CFITL公式重写的有界模型检验算法,并基于后一种算法初步实现了CFITL模型检验器原型工具.后续工作将围绕以下3方面展开:1)对CFITL逻辑系统的逻辑性质进行更深入地研究,包括表达能力和证明系统等;2)研究可行的抽象技术,适用于路径敏感的CFITL模型检验方法;3)基于C语言编程环境,完善VerTPCFG系统,集成各种复杂数据类型的处理功能及更丰富的可视化环境的支撑,使之能处理各类复杂程序. [1]Ben-Ari M, Pnueli A, Manna M. The temoral logic of branching time[J]. Acta Informatica, 1981, 20(3): 207-226[2]Huth M, Ryan M. Logic in Computer Science: Modelling and Reasoning about System[M]. Cambridge, UK: Cambridge University Press, 2004[3]Kwiatkowska M. Model checking for probability and time: From theory to practice[C]Proc of the 18th IEEE Symp on Logic in Computer Science. Piscataway, NJ: IEEE, 2003: 351-360[4]Panangaden P. Labelled Markov Processes[M]. London: Imperial College Press, 2009[5]Clarke E M, Grumberg O, Peled D A. Model Checking[M]. Cambridge, MA: MIT Press, 1999[6]Burch J R, Clarke E M, McMillan K L, et al. Symbolic model checking: 1020states and beyond[J]. Information and Computation, 1992, 98(2): 142-170[7]Alur R, Courcourbetis C, Dill D. Model checking for real-time systems[C]Proc of the 5th Symp on Logic in Computer Science. Piscataway, NJ: IEEE, 1990: 414-425[8]Ball T, Majumdar R, Millstein T D, et al. Automatic predicate abstraction of C programs[C]Proc of the 22nd ACM SIGPLAN Conf on Programming Language Design and Implementation. New York: ACM, 2001: 203-213[9]Clarke E M, Biere A, Raimi R. Bounded model checking using satisfiability solving[J]. Formal Methods in System Design, 2001, 19(1): 7-34[10]Miller S P, Whalen M W, Cofer D D. Software model checking takes off[J]. Communications of the ACM, 2010, 53(2): 58-64[11]Cordeiro L, Fischer B, Marques-Silva J. SMT-based bounded model checking for embedded ANSI-C software[J]. IEEE Trans on Software Engineering, 2012, 38(4): 957-974[12]Dill D L, Clarke E M. Automatic verification of asynchronous circuits using temporal logic[J]. IEE Proceedings E Computers and Digital Techniques, 1986, 133(5): 276-282[13]Bujang S D A, Selamat A. Verification of mobile SMS application with model checking agent[C]Proc of the 8th Int Conf on Intelligent Systems Design and Applications. Piscataway, NJ: IEEE, 2008: 217-222[14]Alur R, Jagadeesan L J, Kott J J, et al. Model-checking of real-time systems: A telecommunications application: Experience report[C]Proc of the 19th Int Conf on Software Engineering. Piscataway, NJ: IEEE, 1997: 514-524[15]Witkowski T, Blanc N, Kroening D, et al. Model checking concurrent Linux device drivers[C]Proc of the 22nd IEEEACM Int Conf on Automated Software Engineering. New York: ACM, 2007: 501-504[16]Chen H, Dean D, Wagner D. Model checking one million lines of C code[C]Proc of the 11th Symp on Network and Distributed System Security. Washington DC: Internet Society, 2004: 171-185[17]Necula G C. Proof-carrying code[C]Proc of the 24th ACM SIGPLAN-SIGACT Symp on Principles of Programming Languages. New York: ACM, 1997: 106-119[18]Bozga M, Iosif R, Perarnau S. Quantitative separation logic and programs with lists[J]. Journal of Automated Reasoning, 2010, 45(2): 131-156[19]Löding C, Lutz C, Serre O. Propositional dynamic logic with recursive programs[J]. Journal of Logic and Algebraic Programming, 2007, 73(1): 51-69[20]Flanagan C, Leino C K R, Lillibridge M, et al. Extended static checking for Java[C]Proc of the 23rd ACM SIGPLAN Conf on Programming Language Design and Implementation. New York: ACM, 2002: 234-245[21]King J C. Symbolic execution and program testing[J]. Communications of the ACM, 1976, 19(7): 385-394[22]Ma K K, Phang K Y, Jeffrey S F. Directed symbolic execution[G]LNCS 6887: Proc of the 18th Int Conf on Statis Analysis. Berlin: Springer, 2011: 95-111[23]Saswat A, Godefroid P, Tillmann N. Demand-driven compositional symbolic execution[G]LNCS 4963: Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2008: 367-381[24]Rosu G, Havelund K. Rewriting-based techniques for running verification[J]. Journal of Automated Software Engineering, 2005, 12(2): 151-197[25]Nieuwenhuis R, Oliveras A, Tinelli C. Solving SAT and SAT modulo theories: From an abstract DPLL procedure to DPLL(T)[J]. Journal of ACM, 2006, 53(6): 937-977[26]Böhm C, Jacopini G. Flow diagrams, turing machines and languages with only two formation rules[J]. Communications of the ACM, 1966, 9(5): 366-371[27]Harel D. On folk theorems[J]. Communications of the ACM, 1980, 23(7): 379-389[28]Cousot P, Cousot R. Abstract interpretation: A unified lattice model for the static analysis of programs by construction or approximation of fixpoints[C]Proc of the 4th ACM SIGPLAN-SIGACT Symp on Principles of Programming Languages. New York: ACM, 1977: 238-252[29]Dams D, Gerth R, Grumberg O. Abstract interpretation of reactive systems[J]. ACM Trans of Program Language System, 1997, 19(2): 253-291[30]Zhang L, Malik S. The quest for efficient boolean satisfiability solvers[G]LNCS 2404: Proc of the 14th Int Conf on Computer Aided Verification. Berlin: Springer, 2002: 17-36[31]Zhang H. SATO: An efficient propositional prover[G]LNAI 1249: Proc of the 14th Int Conf on Automated Deduction. Berlin: Springer, 1997: 272-275[32]Moura L D. Z3: An efficient SMT solver[G]LNCS 4963: Proc of the 14th Int Conf on Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2008: 337-340[33]Fraser G, Wotawa F. Using LTL rewriting to improve the performance of model checker based test case generation[C]Proc of the 3rd Workshop on Advances in Model Based Testing. New York: ACM, 2007: 64-74[34]Clarke D, Jeron T, Rusu V. STG: A symbolic test generation tool[G]LNCS 2280: Proc of the 8th Int Conf on Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2002: 152-173[35]Tang Zhisong, Zhao Chen. A temporal logic language oriented toward software engineering[J]. Journal of Software, 1994, 5(12): 1-16 (in Chinese)(唐稚松, 赵琛. 一种面向软件工程的时序逻辑语言[J]. 软件学报, 1994, 5(12): 1-16)[36]Zhu Xueyang. The dual software architecture description framework XYZADL[J]. Journal Computer Research and Development, 2007, 44(9): 1485-1494 (in Chinese)(朱雪阳. 双重软件体系结构描述框架XYZADL[J]. 计算机研究与发展, 2007, 44(9): 1485-1494)[37]Reynolds J C. Separation logic: A logic for shared mutable data structure[C]Proc of the 17th Annual IEEE Symp on Logic in Computer Science. Piscataway, NJ: IEEE, 2002: 55-74[38]Zhao J H, Li X D. Scope logic: An extension to hoare logic for pointers and recursive data structures[G]LNCS 8049: Theoretical Aspects of Computing. Berlin: Springer, 2013: 409-426[39]Balbiani P, Vakarelov D. PDL with intersection of programs: A complete axiomatization[J]. Journal of Applied Non-Classical Logics, 2003, 13(4): 231-276 [40]Chen Yiyun, Hua Baojian, Ge Lin, et al. A pointer logic for safety verification of pointer programs[J]. Chinese Journal of Computers, 2008, 31(3): 372-380 (in Chinese)(陈意云, 华保健, 葛琳, 等. 一种用于指针程序安全性证明的指针逻辑[J]. 计算机学报, 2008, 31(3): 372-380)[41]Li Z P, Zhang Y, Chen Y Y. A shape graph logic and a shape system[J]. Journal of Computer Science & Technology, 2003, 28(6): 1063-1084[42]Li Guangyuan, Tang Zhisong. Representing and verifying reactvie systems with continuous-time temporal logic[J]. Chinese Journal of Computers, 2003, 26(11): 1424-1434 (in Chinese)(李广元, 唐稚松. 反应系统的连续时序逻辑表示和验证[J]. 计算机学报, 2003, 26(11): 1424-1434)[43]Lin Chang, Qu Yang, Li Yajuan. Modeling, consistency and inference of extended interval temporal logic[J]. Chinese Journal of Computers, 2002, 25(12): 1338-1347 (in Chinese)(林闯, 曲杨, 李雅娟. 扩展时段时序逻辑的模型、一致性和推理[J]. 计算机学报, 2002, 25(12): 1338-1347)[44]Bresolin D, Monica D D, Montanari A, et al. The light side of interval temporal logic: The Bernays-Schonfinkel fragment of CDT[J]. Annals of Mathematics and Artificial Intelligence, 2014, 71(1): 11-39[45]Moszkowski B. Reasoning about digital circuits, STAN-CS-83-970[R]. Palo Alto, CA: Stanford University, 1983[46]Halpern J, Shoham Y. A propositional modal logic of time intervals[J]. Journal of ACM, 1991, 38(4): 935-962[47]Duan Zhenhua. An extended interval temporal logic and a framing technique for temporal logic programming[D]. Newcastle Upon Tyne, UK: Newcastle University, 1996[48]Tian Cong, Duan Zhenhua. Model checking rate monotone scheduling algorithm based on propositional projection temporal logic[J]. Journal of Software, 2011, 22(2): 211-221 (in Chinese)(田聪, 段振华. 基于命题投影时序逻辑的单调速率调度算法模型检测[J]. 软件学报, 2011, 22(2): 211-221) Chen Donghuo, born in 1974. PhD, lecturer. Member of China Computer Federation. His main research interests include program verification, model checking, and automated reasoning. Liu Quan, born in 1969. Post doctor, professor and PhD supervisor. Senior member of China Computer Federation. His main research interests include intelli-gence information processing, automated reasoning, and machine learning. Jin Haidong, born in 1973. PhD candidate, lecturer. His main research interests include reinforcement learning, and human-computer interaction. Zhu Fei, born in 1978. PhD, associate professor. Member of China Computer Federation. His main research interests include reinforcement learning, text mining, and pattern recognition. Wang Hui, born in 1968. PhD candidate, lecturer. Member of China Computer Federation. His main research interests include machine learning, and human-computer interaction. A Temporal Logic with a Semantics Defined on the Static Structure and Dynamic Behavior of Program Chen Donghuo1, Liu Quan1,2, Jin Haidong1, Zhu Fei1,2, and Wang Hui1 1(SchoolofComputerScienceandTechnology,SoochowUniversity,Suzhou,Jiangsu215006)2(KeyLaboratoryofSymbolicComputationandKnowledgeEngineering(JilinUniversity),MinistryofEducation,Changchun130012) The paper presents an interval temporal logic—CFITL(control flow interval temporal logic) which is used to specify the temporal properties of abstract model of program, for example control flow graph, generally abbreviated to CFG. The targeted logic differs from the general sense of temporal logics, typically CTL and LTL, whose semantical models are defined in term of the state-based structures. The semantics of CFITL is defined on an ordered CFG structure, which encodes the static structure and dynamic behavior of program. The ordered CFGs are a subset of CFGs, and their topology can be summarized by partially ordered sets, such that the induced natural number intervals can be mapped onto the well-formed structures of program. In other words, the CFITL formulae have the ability of specifying the properties related to not only the dynamic behavior but also static structure of programs. After the syntax and semantics of CFITL are expounded, the problem of model checking over CFITL is detailedly discussed. Furthermore, two types of algorithms are designed: one is based on the computation of reachable state space as well as the another is based on bounded model checking employing the SMT(satisfiability modulo theories) solvers power. Because programs implemented by advanced programming languages inevitably involve complex abstract data types with unbounded domains and operators, and the semantics of CFITL is more complex than the one of CTL, the method of SMT based model checking is more practical than the method of direct search of state space. In the sequel, a prototype tool is implemented, and some case studies are conducted. interval temporal logic; control flow graph (CFG); static structure of program; model checking; satisfiability modulo theories (SMT) 2015-05-14; 2016-02-16 国家自然科学基金项目(61272005,61303108,61373094,61472262,61502323,61502329);江苏省自然科学基金项目(BK2012616);福建省自然科学基金项目(2014J01221);江苏省高校自然科学研究项目(13KJB520020);吉林大学符号计算与知识工程教育部重点实验室项目(93K172014K04);苏州市应用基础研究计划项目(SYG201422) This work was supported by the National Natural Science Foundation of China (61272005, 61303108, 61373094, 61472262, 61502323, 61502329), the Natural Science Foundation of Jiangsu (BK2012616), the Natural Science Foundation of Fujian Province (2014J01221), the High School Natural Foundation of Jiangsu (13KJB520020), the Project Funded by the Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University (93K172014K04), and the Suzhou Industrial Application of Basic Research Program (SYG201422). 刘全(quanliu@suda.edu.cn) TP311

2 模型检验














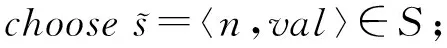
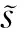







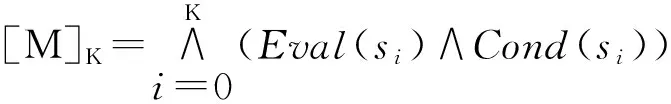
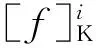




3 VerTPCFG模型检验器


4 相关工作
5 总 结





