可保障数据无中断传输的冗余树算法研究
2016-10-13罗军舟
夏 怒 李 伟 陆 悠 蒋 健 单 冯 罗军舟
(东南大学计算机科学与工程学院 南京 211189)
可保障数据无中断传输的冗余树算法研究
夏怒李伟陆悠蒋健单冯罗军舟
(东南大学计算机科学与工程学院南京211189)
(xia_nu@seu.edu.cn)
随着大数据应用的发展,保障数据无中断传输的需求日益增强.针对单点或单链路失效的情况,现有的保障数据无中断传输方法存在主备份路径的数据传输性能较低、抵御多节点边失效能力不强等问题.为解决以上问题,提出一种可保障数据无中断传输的按边序选环的冗余树算法CSES(circle selecting by edge sorting based redundant tree algorithm for uninterrupted data delivery),可用于构建数据传输性能优化的主备份路径,并使数据传输具有较强的抵御多节点边失效的能力. 该算法首先根据网络拓扑构建以数据源为根节点的最小传输树,以最小化主传输路径上的转发跳数;其次,为了减少备份路径的转发跳数并提高数据传输抵御多节点边失效的能力,对拓扑中不在最小传输树上的边进行排序,将树上根节点到边上2个端点的路径上节点数量之和较小的边排在前列. 随后按序将边添加到最小传输树上以构建冗余环,并基于冗余环生成冗余枝添加到最小传输树上,最终形成以数据源为根节点的冗余树.实验结果表明,相比于其他冗余树算法,基于CSES算法构建的冗余树所生成的主备份路径的转发跳数更少且抵御多节点边失效的能力更强.
数据无中断传输;最小传输树;边排序;冗余环;冗余树
随着新型应用以及网络用户数量的快速增长,各个领域的数据量急剧增加,为了充分利用大数据资源,当前绝大多数研究是围绕数据挖掘、机器学习以及数据分析等方面展开的,而在网络对大数据的支撑方面所做的研究甚少.正如文献[1]指出:研究大数据传输对于大数据应用发展的重要意义;数据中心网络是支撑大数据传输的核心设施,近年来随着MapReduce、虚拟机迁移等数据应用的发展,愈来愈多的数据需要在数据中心内传输以用于处理和分析,因此数据中心网络对数据传输的支撑能力直接影响到大数据应用的部署与发展.然而,随着数据中心网络规模日益扩大以及网络结构日趋复杂化,影响网络稳定性的因素如人为配置错误、恶意攻击、软件漏洞、路由节点或链路硬件故障等逐渐增多,同时由于数据中心网络中广泛采用了低成本的网络设备,致使数据中心网络面临愈来愈严重的节点和链路失效风险,当前数据中心支撑的应用在执行过程中往往需要在短时间内传输少量数据(TCP短流)以实时地响应用户请求(数据库查询、使用WEB服务等).对于这类应用需求,一个很重要的要求就是快速响应,从而数据传输的可靠性对此类应用的执行性能有很大影响.此外还值得注意的是,虽然TCP 短流理应和 TCP 长流获得相等的网络资源,然而在实际中却是TCP长流占据了大部分链路带宽,这导致例如当别的用户在下载大文件时一些用户打开简单网页的时间都会指数上升,因此如果不能保障TCP长流快速无中断地传输,也会增大TCP短流在传输队列中的等待时间进而降低应用响应用户请求的速度.因此,需要数据中心网络能够提供有效的失效恢复策略和容错机制来保障数据传输的可靠性.遗憾的是,有研究表明:现有数据中心网络针对网络节点失效的容错性较差[2],基于链路状态协议重新计算数据传输路径[3-4]往往导致路由收敛时间过长,无法满足实时性要求较高的数据应用的需要.因此,研究可保障数据无中断传输的技术具有重要意义.
需要指出的是,虽然数据中心网络拓扑具有其自身的特点,然而以Fat-tree[5]为代表的数据中心网络拓扑中每个中间节点可以有多个父节点,即增加了上下层集合交换机之间以及集合交换机与核心交换机之间的链路,从而较大幅度地增大了网络的连通性,使得一对交换节点之间有多条路径相连,因此基于Fat-tree的数据中心网络中3个层次的交换设备所构成的网络拓扑可抽象成一般网络拓扑,特别是以Camdoop[6]为代表的服务器互连并将服务器作为数据处理转发节点的数据中心网络中,服务器组成的网络拓扑与一般网络拓扑更为接近并且连接度更大.
为了实现数据无中断传输,从网络故障发生后减少恢复数据传输所需时间的角度出发,相比发生节点或链路失效时再重新寻找备份路径的方法[3-4,7],预先计算数据传输备份路径被视为一种有效方法.文献[8]针对由节点失效或路径拥塞所导致数据无法继续转输的情况,将失效路径上正在转发的数据转移到另一条预先设置的备份路径上,进而提高数据传输可靠性.文献[9]为了提高备份路径的负载均衡以及QoS,提出了在拓扑中为数据传输路径尽力寻找与其分离度最高且跳数相近的备份路径的方法.文献[10]认为网络中每个链路的失效概率并不相同,因此首先对链路的重要性进行评估,然后根据评估结果有选择地为重要链路预先计算与其不相交的冗余路径.文献[11]为拓扑中每一对节点设置多条备份路径,以便当网络故障发生时在保障数据无中断传输的同时实现负载均衡.然而,上述方法针对每条链路或每个节点失效寻找备份路径时需要反复深度遍历网络拓扑,导致算法复杂度较高.值得注意的是,由于冗余树算法在保障数据无中断传输方面具有算法复杂度较小、故障恢复时间短等特点[12],逐渐引起研究者的关注,其中Médard等人提出的冗余树算法MFBG[13]被广泛使用并被认为对未来网络故障快速恢复技术的发展具有重要意义[14].MFBG算法通过在网络拓扑中随机构建环的方式构建蓝、红2棵树,这2棵树具有共同的根节点,蓝树用作数据传输的主树(primary tree),红树则为备份树(secondary tree),在移除拓扑中任意1个节点或1条边后,剩余的节点仍然可以通过2棵树中的1棵与根节点保持连通.然而,该算法在构建冗余树时未考虑对路径传输性能如延迟和开销等进行优化,因此其所采取的随机选环方式导致主备份路径的传输性能不佳.一些学者基于MFBG算法展开进一步研究,文献[15]提出了仅仅利用本地信息构建红蓝2棵树的方法,文献[16]通过尽可能多地将拓扑中的边加入主传输树(蓝树)以期在故障发生后降低启用备份路径的频率进而降低恢复开销,文献[17]构建路径长度接近的红蓝2棵树以平衡主备份传输路径的性能.然而,上述方法在多点边失效的情况下会有较多的节点失去与数据源节点的连接,抵御多节点边失效的能力较差,并且同样未对红树和蓝树上路径传输性能进行优化.尽管Xue等人对MFBG算法做出改进并提出了G-MFBG算法[18],优先选择传输性能较好的路径作为主传输路径(蓝树上路径),然而,由于G-MFBG算法仍然是基于MFBG算法所提出的先在拓扑中生成环再构建红蓝2棵树的思想,这导致主传输树(蓝树)上路径传输性能无法达到最优化,同时,该算法也没有考虑优化备份传输树(红树)上的路径传输性能.因此,上述方法均无法满足数据传输对于延迟等性能指标的要求[19].综上所述,对于大数据传输,不仅要保障数据无中断传输,还要保障数据传输性能.
考虑到在数据中心网络中选择转发跳数较小的路径可以减少数据传输延迟、提高流量转发效率、降低路由节点或链路失效对数据传输的影响[20],因此,为了保障无中断数据传输并且降低数据传输路径的转发跳数,本文提出了一种可保障数据无中断传输的按边序选环的冗余树算法CSES(circle selecting by edge sorting based redundant tree algorithm for un-interrupted data delivery).首先,为了减少主传输路径的转发跳数,本算法根据网络拓扑以数据源为根节点构建1棵最小传输树作为主传输路径,该树上根节点与其他节点之间的转发跳数是最少的;其次,为了降低备份路径的转发跳数并提高抵御多节点边失效的能力,对拓扑中不在最小传输树上的边进行排序,将树上根节点到边上2个端点的路径上节点数量之和较小的边排在前列;随后,依次将这些边添加到最小传输树上构成冗余环,并基于冗余环生成冗余枝添加到最小传输树上,最终形成1棵冗余树.实验结果表明,相比于其他冗余树算法,基于本文算法构建的冗余树所生成的主备份路径的转发跳数更少并且抵御多节点边失效的能力更强.
1 问题描述
在数据中心网络中,当某个节点需要向其他节点发送数据时,该节点为数据源节点,其他节点为目的节点.本文的目标是为数据源节点构建到达目的节点之间具有最小转发跳数的传输路径,并且保障在网络中出现单节点或单链路失效时可通过快速启用具有较小转发跳数的备份路径(不经过故障节点或链路的路径)恢复源节点向受网络故障影响的节点传输数据,同时保障数据传输具有较强的抵御多点边失效的能力.
为方便描述本文所采用的方法,将网络抽象成1个无向图G(V,E).其中,V为网络拓扑中的节点集合,每个节点表示1个网络设备;E为网络拓扑中的边集合,每条边表示1条直接连接2个网络设备的数据传输链路.任选拓扑中1个节点为数据源节点,本文期望构建1棵以数据源节点为根节点的冗余树,该树同时包含转发跳数优化的主备份路径.在冗余树上出现任意1个节点(根节点除外)或1条边失效的情况下,冗余树的根节点仍然可以通过树上的备份路径与其他节点保持连接,在多点边失效的情况下,可有效保障冗余树的根节点与树上其他尽可能多的节点的连通性.需要指出的是,虽然为满足实时性较强的应用对数据传输可靠性的需求是本文的主要关注点,然而本文的算法理念与负载均衡技术并不冲突:当路径负载较小时,为保障数据传输的效能和可靠性,可选取最小跳数传输路径进行数据传输;而当路径负载较大时,可多路径均衡负载即主传输路径和备份路径都可以用于同时传输数据,在出现节点或链路故障时,主传输路径与备份路径互为冗余以实现无中断数据传输.
为确保在单节点或单边失效情况下能够为拓扑中节点寻找到冗余树根节点与之相连的备份路径,与其他冗余树算法一样,本文也假设网络拓扑中任意2个节点之间至少存在2条节点和边均互不相交的路径,由于基于Fat-tree[5]以及Camdoop[6]技术的数据中心网络中数据交换节点(交换机或服务器)之间的连通性非常丰富,因此上述假设的合理性得以保障.一个满足本文假设的网络拓扑如图1所示:
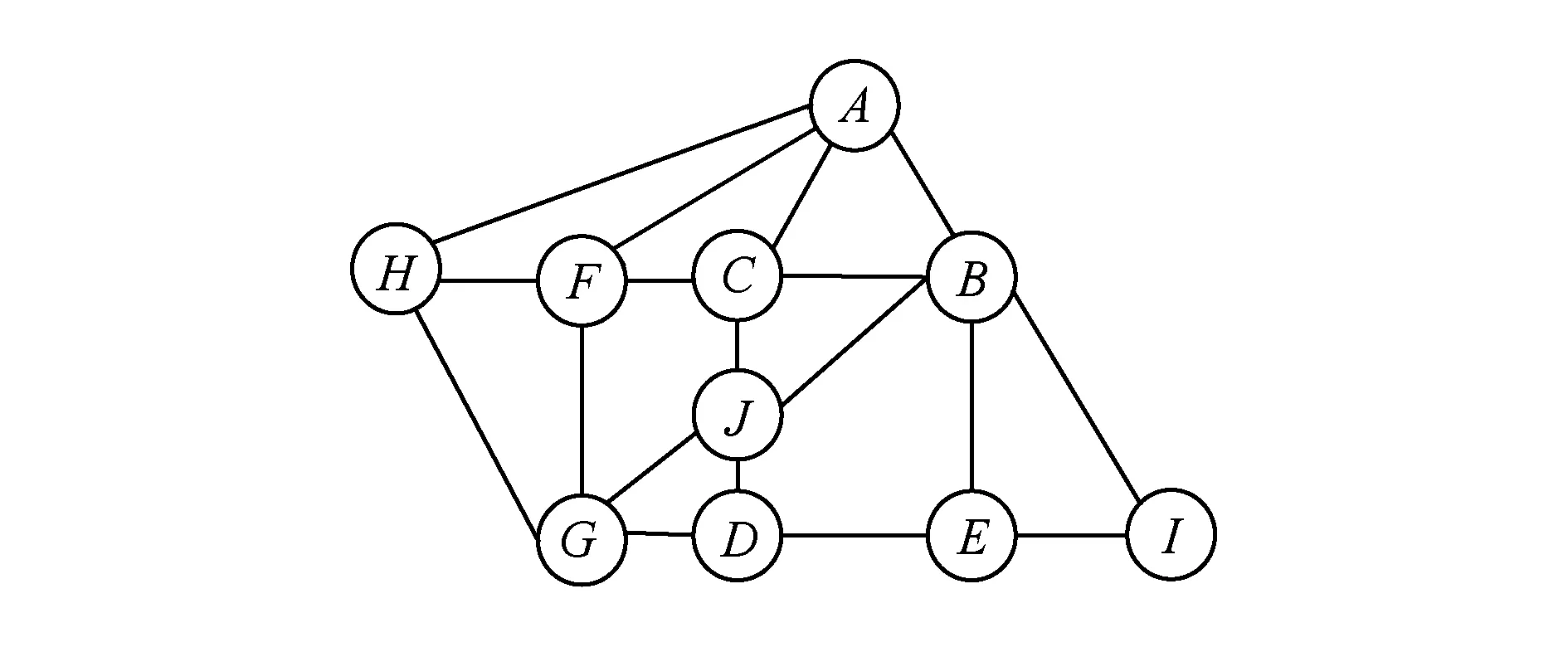
Fig. 1 Network topology.图1 网络拓扑
2 冗余树算法思想
基于引言对现有保障数据无中断传输的冗余树算法的分析,为了减少主备份传输路径的转发跳数,本文不采取先构建环再生成主备份传输路径的方式,而是首先基于Dijkstra算法建立1棵最小传输树作为主传输路径.
定义1. 最小传输树.是网络拓扑中1棵以节点s为根节点的树,该树上根节点s到其他任意1个节点x的转发跳数是网络拓扑中节点s到节点x的所有路径中转发跳数最少的.
在图1中以节点A为根节点的1棵最小传输树如图2所示:
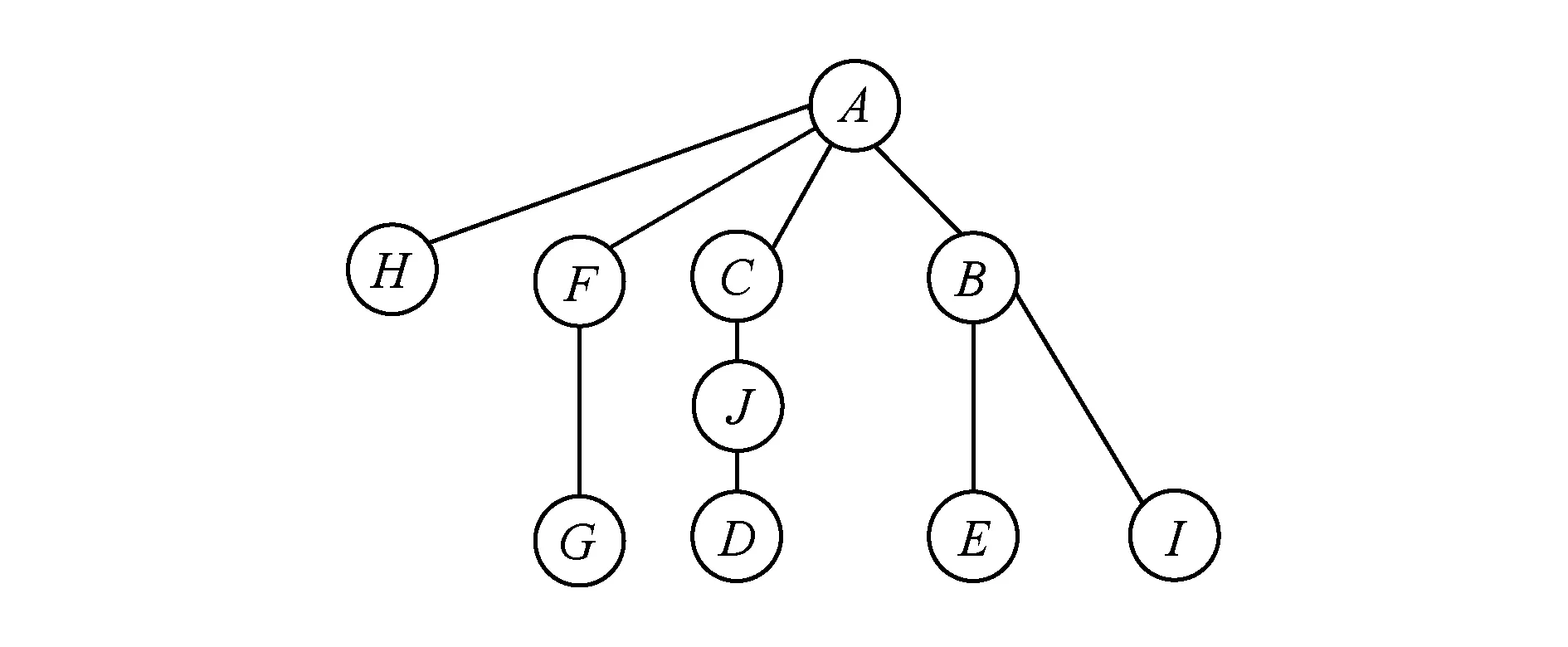
Fig. 2 The minimal delivery tree.图2 最小传输树
2.1基于剩余边排序的选环
本文以通过向最小传输树上添加剩余边构建冗余环的方式为最小传输树上节点寻找转发跳数较少的备份路径.
定义2. 剩余边.是网络拓扑中不在最小传输树上的边.
定义3. 冗余环.是基于剩余边和最小传输树所形成的环,当该环上有1个节点或1条边失效时,环上其他节点与最小传输树根节点之间仍然存在可达路径.
结合图2所示最小传输树可知,图1中的边(B,C)为1条剩余边,将该剩余边加入图2中的最小传输树中,可构成环(A,B,C,A).当该环上任意1个节点(不包含A)或1条边失效时,环上其他节点仍可以与根节点A保持连接,因此该环为冗余环.
然而,需要指出的是,基于不同冗余环所形成的同一节点的备份路径的转发跳数是不同的,由图1和图2可知,包含根节点A和节点G的冗余环有多个,如(A,F,G,J,C,A)和(A,F,G,H,A),当节点F失效时,根节点A到达节点G的备份路径(A,C,J,G)的转发跳数为3,另一条备份路径(A,H,G)的转发跳数则为2.因此,为了给最小传输树上的节点构建具有较少转发跳数的备份路径,本文首先对剩余边按照边的节点度进行排序,然后再进行冗余环的构建.
定义4. 如果剩余边e的2个顶点分别为x和y,则剩余边e的节点度NDe为最小传输树上根节点s分别到节点x和节点y的路径上所包含的节点数量之和.
为了减少备份路径的转发跳数,本文并非随机选择剩余边和最小传输树构建冗余环,而是先为每一条剩余边e计算其节点度NDe,然后根据节点度值从小到大对剩余边进行排序,这样做在减少备份路径的转发跳数的同时也提高了冗余树抵御多点边失效的能力.接着,按照从小到大的顺序依次将剩余边添加到最小传输树上构建冗余环.然而值得注意的是,剩余边和最小传输树所形成的环并非都是冗余环.以图2为例,将剩余边(E,I)加入到最小传输树上,可构成环(B,E,I,B),由于该环上节点B为根节点A到达节点E和节点I必须要经过的节点,一旦节点B失效,则无路径可将节点E和节点I与节点A相连,因此根据定义3可知环(B,E,I,B)不是冗余环.
定理1. 如果1个基于剩余边和最小传输树所形成的环满足以下条件之一:
1) 该环包含根节点;
2) 该环中至少有2个节点属于其他冗余环;
则该环是冗余环.
证明. 1)由于该环包含根节点,所以从该环上去掉除根节点以外的任意1个节点或1条边,该环上剩余节点仍然可以与根节点相连通,根据定义3可知,该环为冗余环.2)由于该环中至少有2个节点属于其他冗余环,不失一般性,设这2个节点分别为x和y,根据定义3可知,节点x和节点y与根节点之间一定存在可达路径,当该环上1个节点(包括节点x和节点y)失效时,该环其他节点至少可以通过节点x和节点y中的1个节点与根节点相连接,因此该环是冗余环.
证毕.
根据定理1,对于由网络拓扑G(V,E)生成的最小传输树和剩余边序列Seq,基于剩余边排序的冗余环构建方法如下:
1) 初始化,令节点集合T={s},其中s为网络拓扑G的最小传输树的根节点,按序将剩余边序列Seq中的剩余边添加到最小传输树上形成相应的环并按序存储这些环.
2) 读取序列Seq中排在最前面的剩余边在最小传输树上形成的环.
3) 如果该环包含根节点s或者至少已有2个节点属于T,则该环为冗余环,将环上不在T中的节点添加到T,同时从Seq中删除该剩余边;否则,读取Seq中的下一条剩余边在最小传输树上形成的环,返回到步骤3)继续执行.
4) 如果T=V或者Seq=∅,则构建冗余环的过程结束,否则返回到步骤2)继续执行.
2.2冗余树的生成
当冗余环上1个节点或1条边失效时,该环上其他节点通过剩余边仍然可达最小传输树的根节点.因此,可以将构成冗余环的剩余边作为冗余枝添加到最小传输树上,从而生成1棵冗余树.假设构成冗余环的剩余边e的2个顶点分别为x和y,那么添加冗余枝的方法如下:
1) 在构建冗余环的过程中,如果构成冗余环的剩余边e只有1个顶点为根节点或已经属于其他冗余环,不失一般性,设该顶点为x,则将边(x,y)添加到最小传输树的节点x上,使得节点y成为节点x在冗余树上的子节点,从而构成根节点通过节点x到达节点y的备份路径.而节点x要么是根节点,要么属于其他冗余环,均已具有根节点可达的备份路径,不需要通过在节点y上添加冗余枝的方式构成根节点到达节点x的备份路径.
2) 在构建冗余环的过程中,如果构成冗余环的剩余边e的2个顶点都不是根节点,也都不属于其他冗余环,则在最小传输树的节点x和节点y上分别添加边(x,y)和边(y,x),形成2条冗余枝,从而分别构成根节点通过节点x到达节点y的备份路径和通过节点y到达节点x的备份路径,最后在1个冗余枝序列中按序将生成的冗余枝加入,该序列用于表示冗余枝加入最小传输树的顺序.
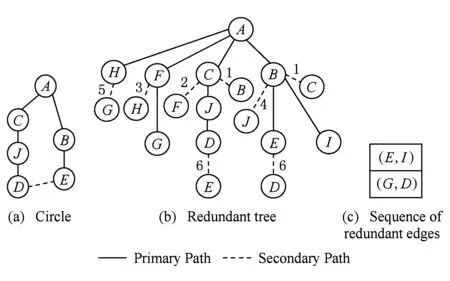
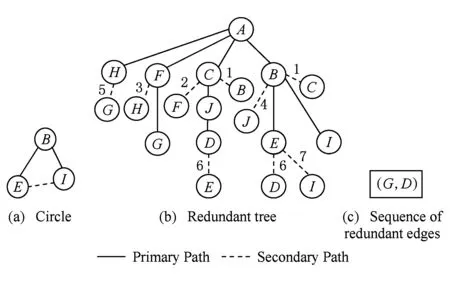
基于上述方法,在选择冗余环的过程中不断添加冗余枝到最小传输树上,直到基于剩余边排序的选环过程结束,最终生成1棵基于最小传输树的冗余树.以图1中节点A作为根节点所生成的冗余树如图3所示(具体生成步骤将作为算法示例在第3节中给出),其中实边表示最小传输树上的边,虚边表示冗余枝,虚边上的标号表示冗余枝被添加到最小传输树上的顺序,标号的目的是为了在根据冗余树生成根节点A到达其他节点的备份下一跳路径时,能够体现对备份路径转发跳数的优化.
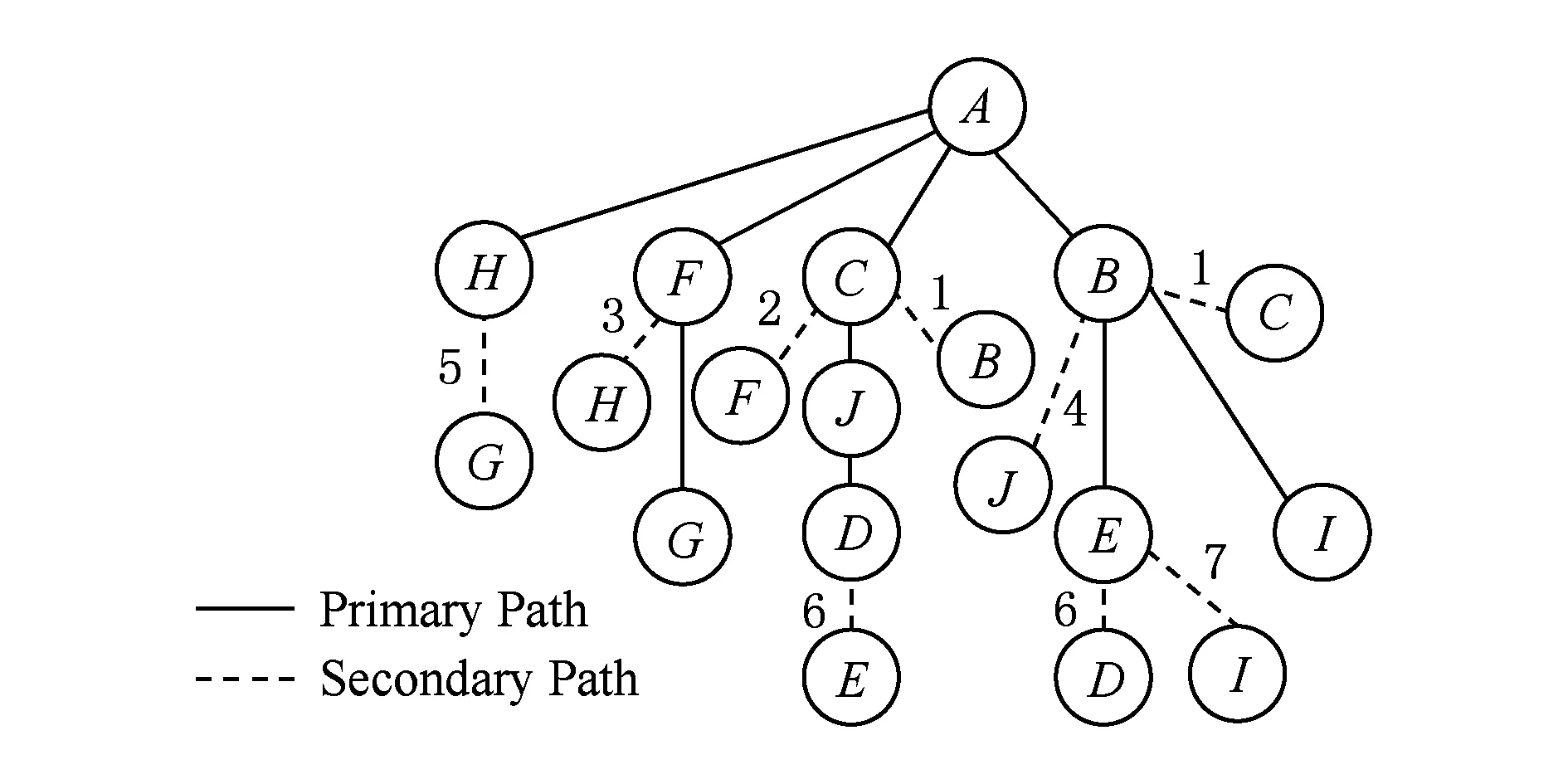
Fig. 3 The redundant tree.图3 冗余树
根据带有冗余枝标号的冗余树,可以生成冗余树上根节点到其他节点的主备份传输路径的路由转发表.对于根节点为s的冗余树,其路由转发表的具体生成方法为:
1) 在冗余树中的最小传输树上,对于根节点s的每一个子节点,分别遍历该子节点的所有子树,将该子节点设为到达自身及其在最小传输树上所有子孙节点的主下一跳.
3) 当所有冗余枝按照生成顺序被遍历完后,根节点s的主备传输路径转发表生成完毕.
根据上述路由转发表的生成方法,以图3为例,节点A的转发表如图4所示.
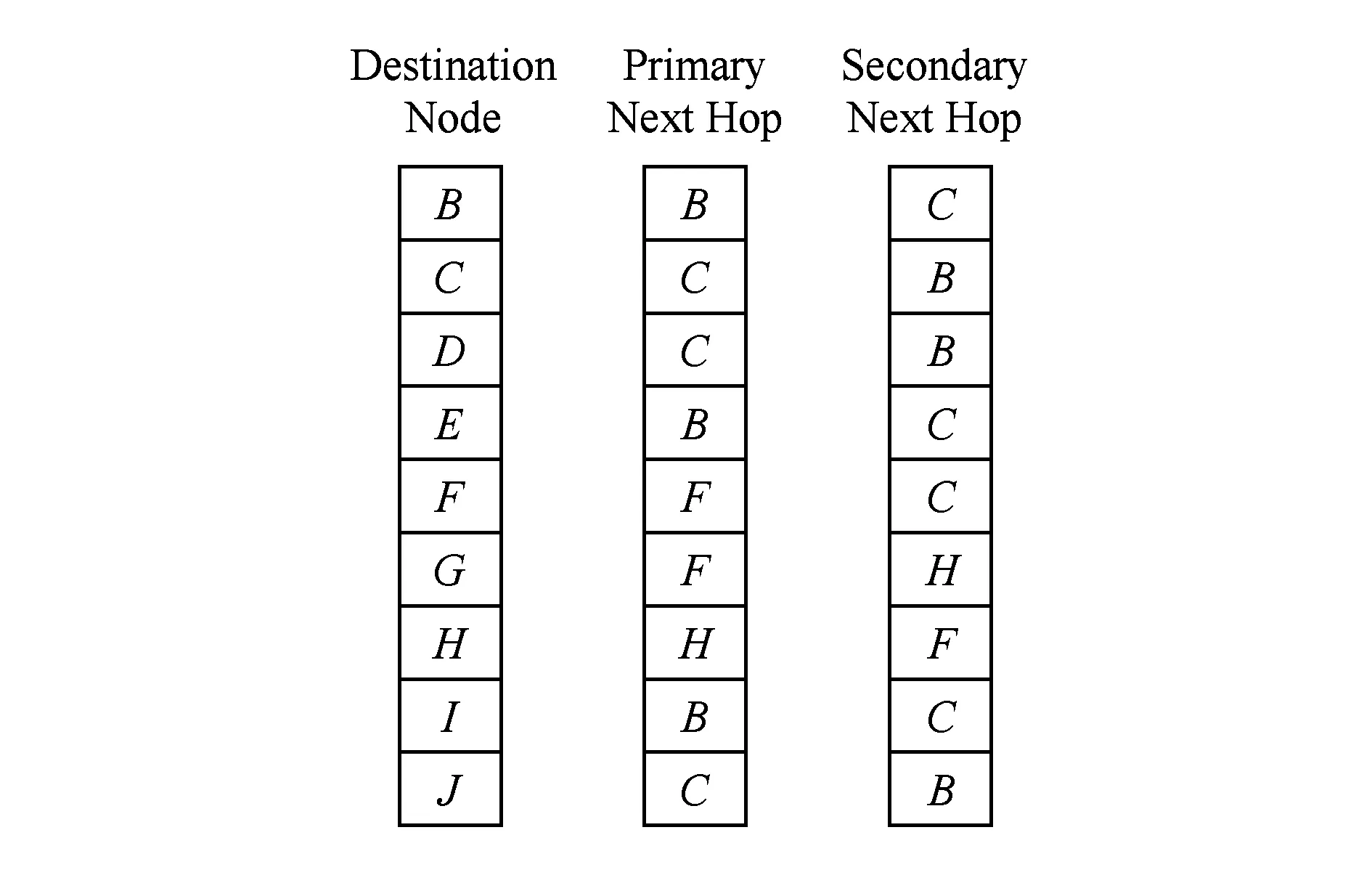
Fig. 4 The forwarding table of the primarysecondary delivery paths for node A.图4 节点A的主备传输路径转发表
3 算法描述
基于第2节对冗余树算法思想的介绍,本节给出冗余树构建算法的具体描述,并通过示例对算法的执行过程进行说明.为方便描述算法,设Ere为剩余边集合,Seq为剩余边序列,用T表示参与冗余环构建的节点集合,对于网络拓扑G(V,E),以s∈V为根节点的冗余树的构建算法如算法1所示:
算法1. 冗余树构建算法.
输入:G(V,E),s,Ere,Seq,T;
输出:冗余树.
①T={s},Ere={},Seq=[];
② 根据G(V,E)和根节点s使用Dijkstra算法构建最小传输树Tr(V,Emin);
(2)真空低温烹饪。将腌制好的鸡翅放入真空包装袋,进行真空包装,放在烤架上,再放入烤箱中间层,选择蒸汽低温烹调模式,调节温度、时间,然后开始低温烹饪。
③Ere=E-Emin;
④ for eache∈Eredo
⑤ 计算边e的节点度NDe;
⑥ 按照节点度值从小到大的顺序将边e插入到Seq中;
⑦ end for
⑧ 按序将Seq中的边加入到Tr中构成相应的环R(Vring),并按序存储这些环;
⑨i=0;*标记冗余枝的添加顺序*
⑩ while (T≠V) do


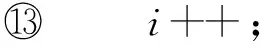





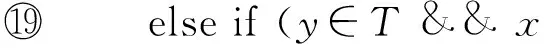






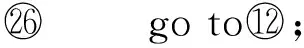
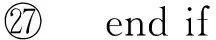


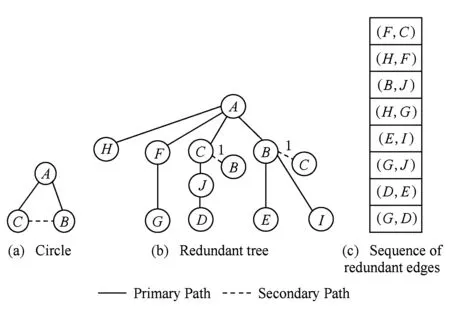
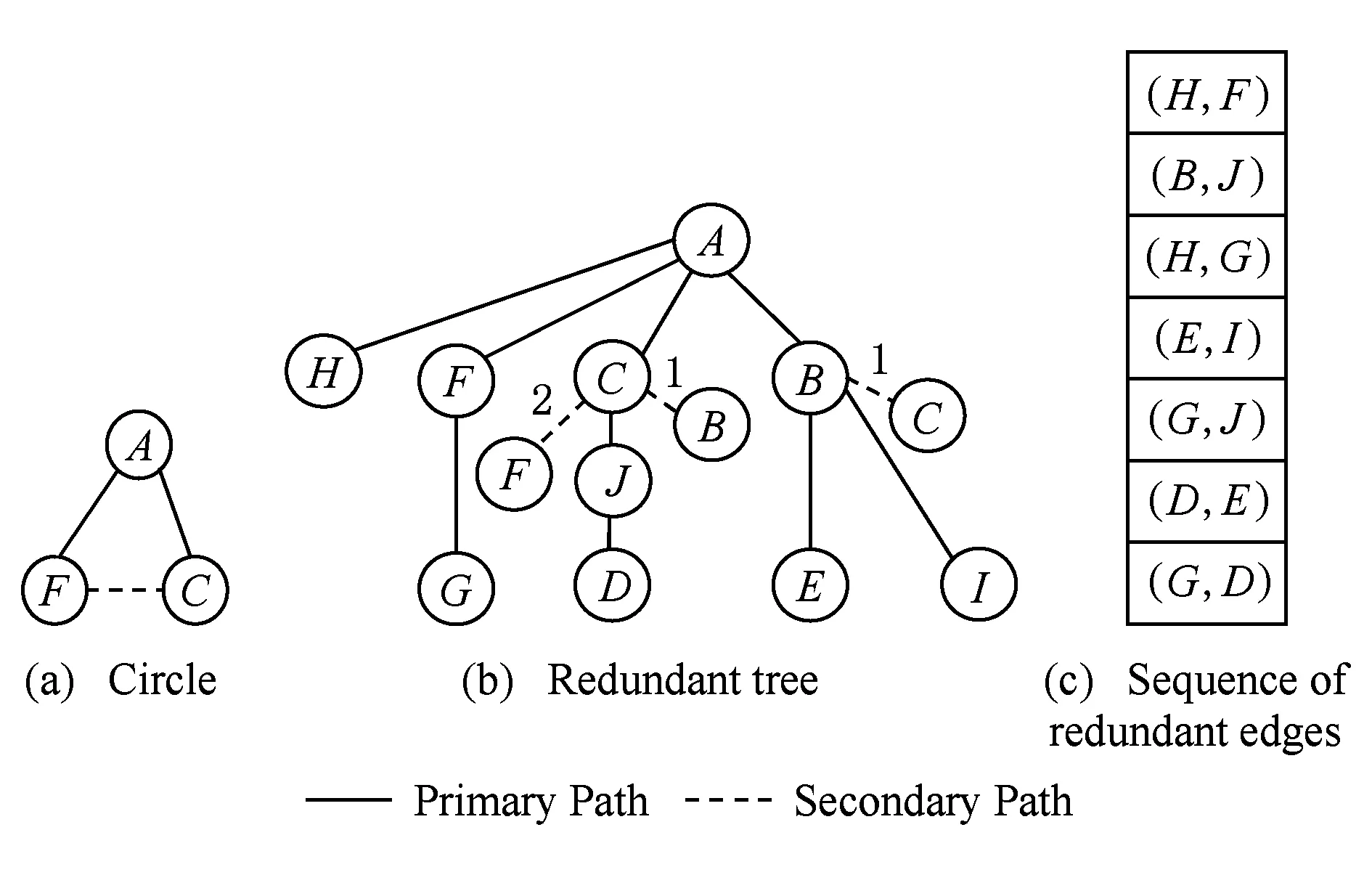
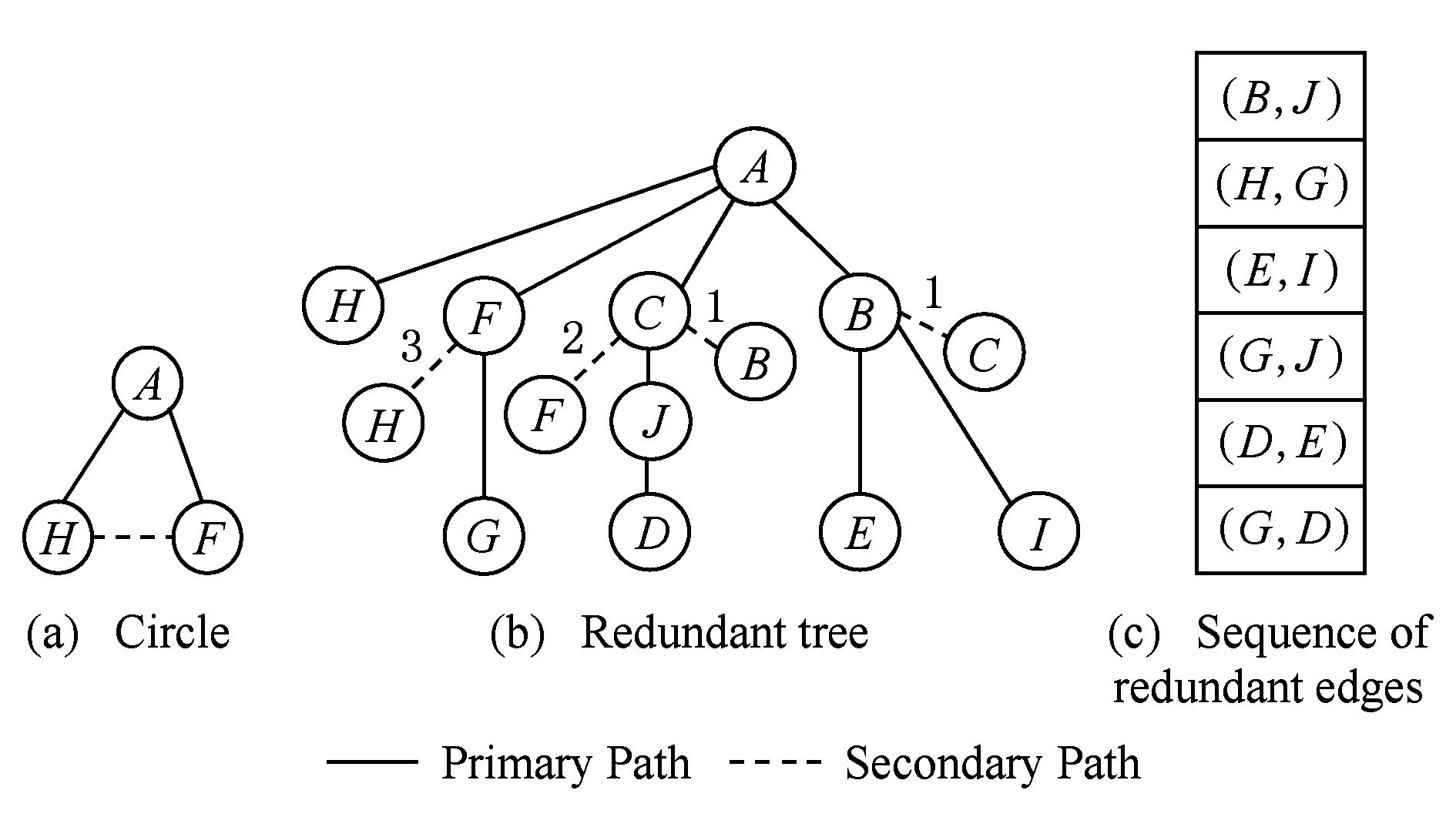
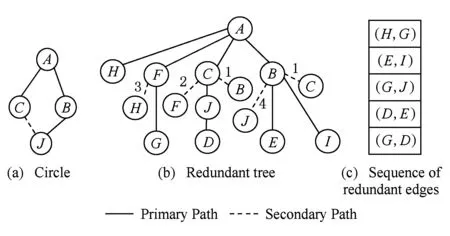
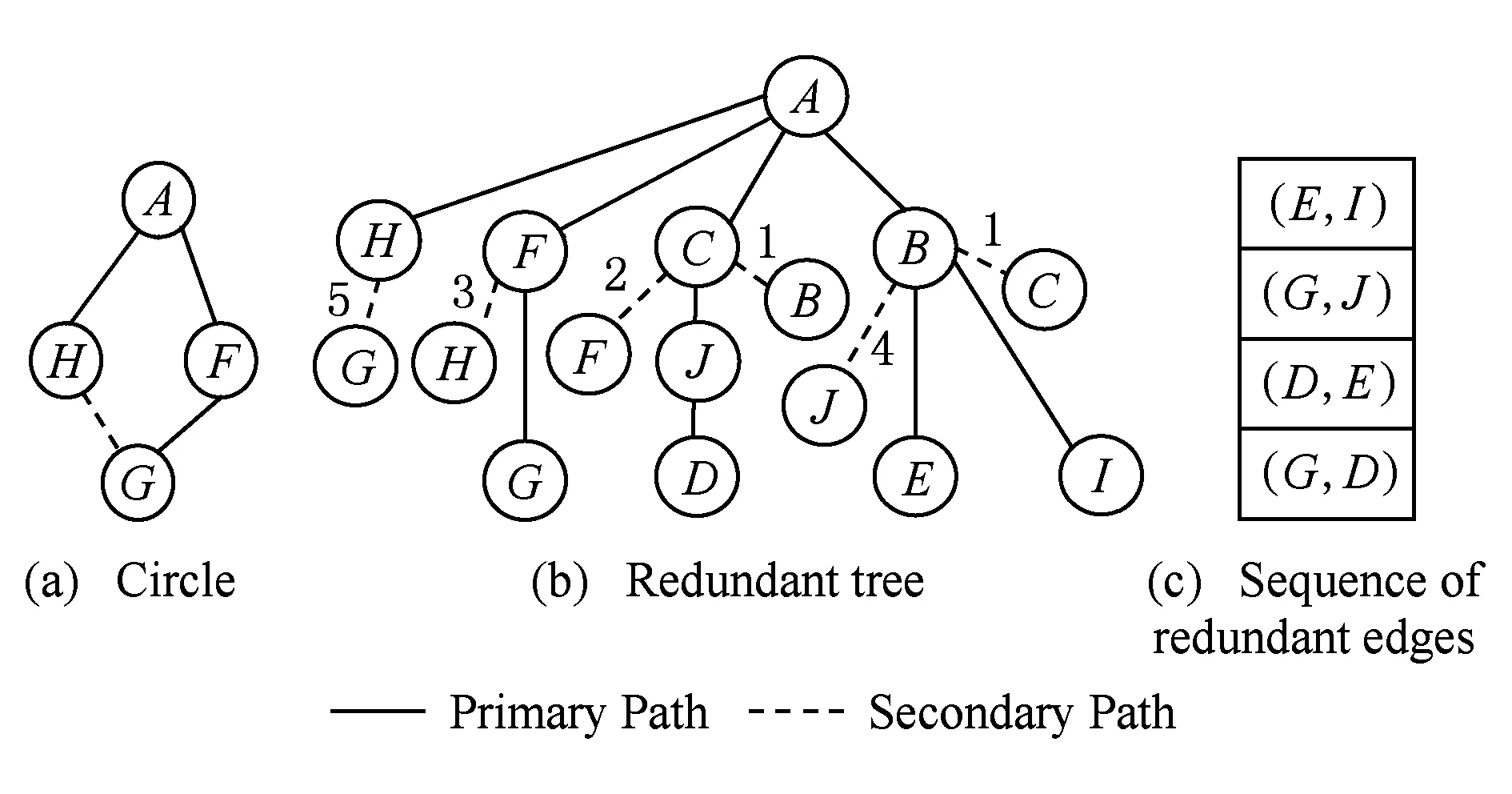
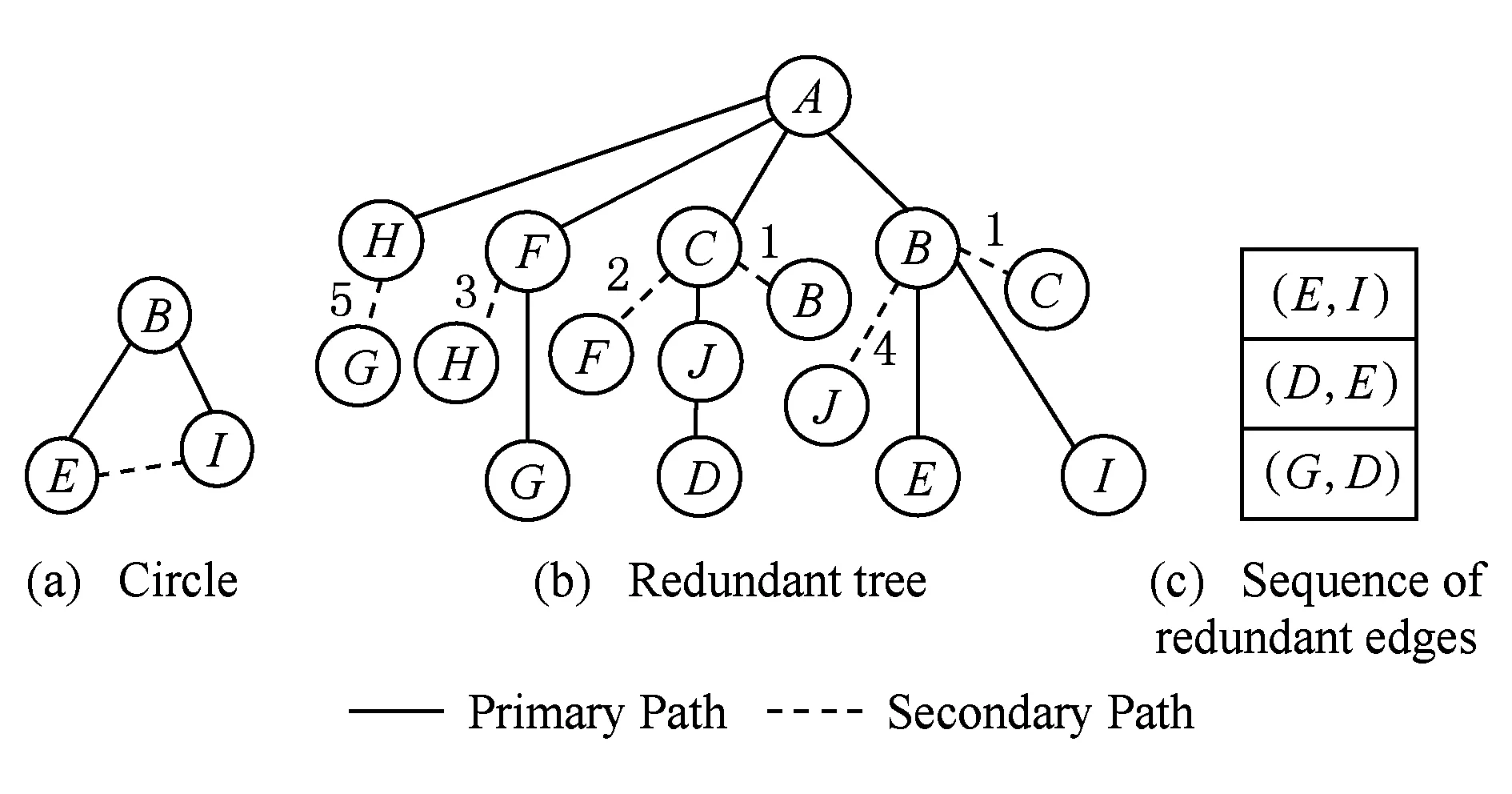
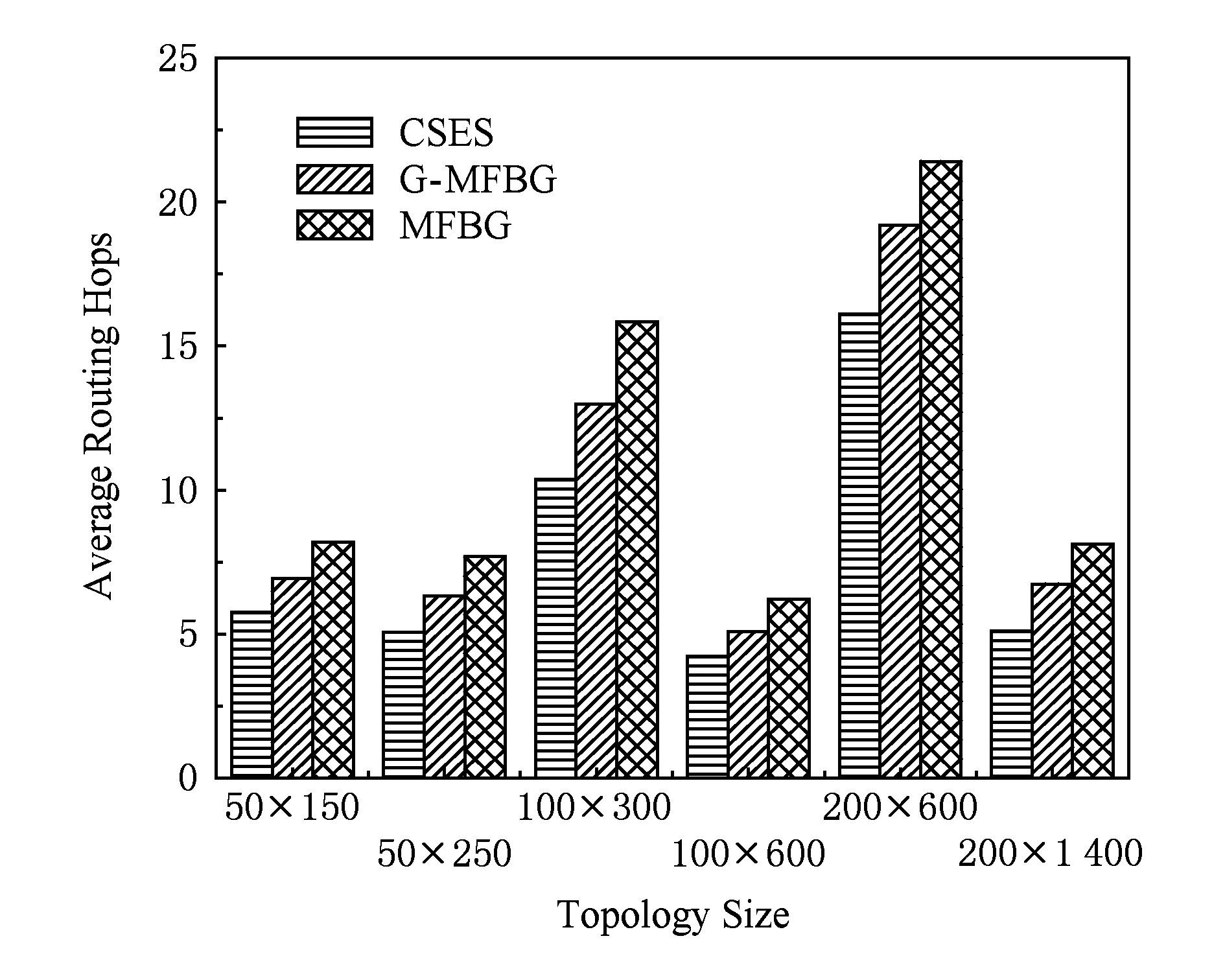
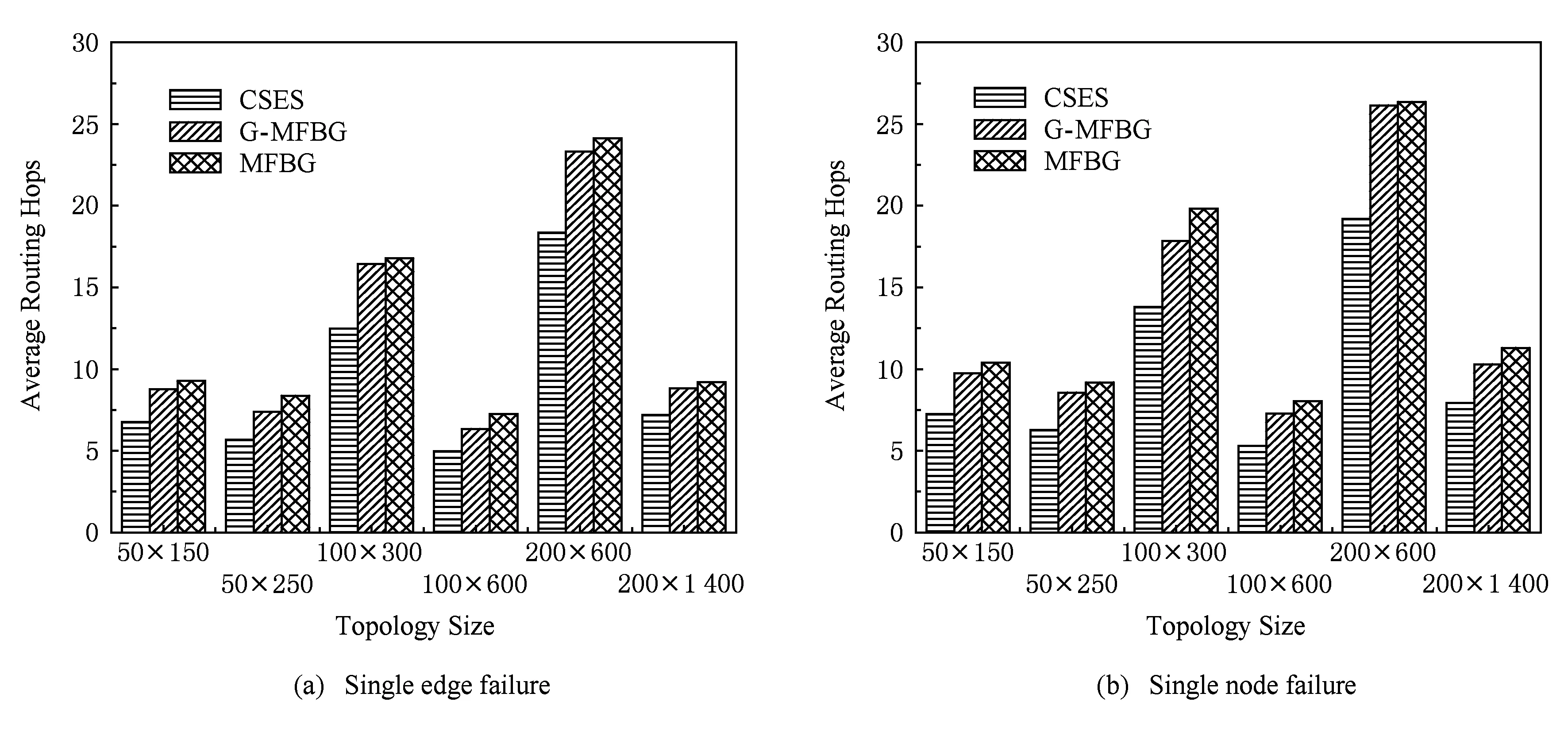
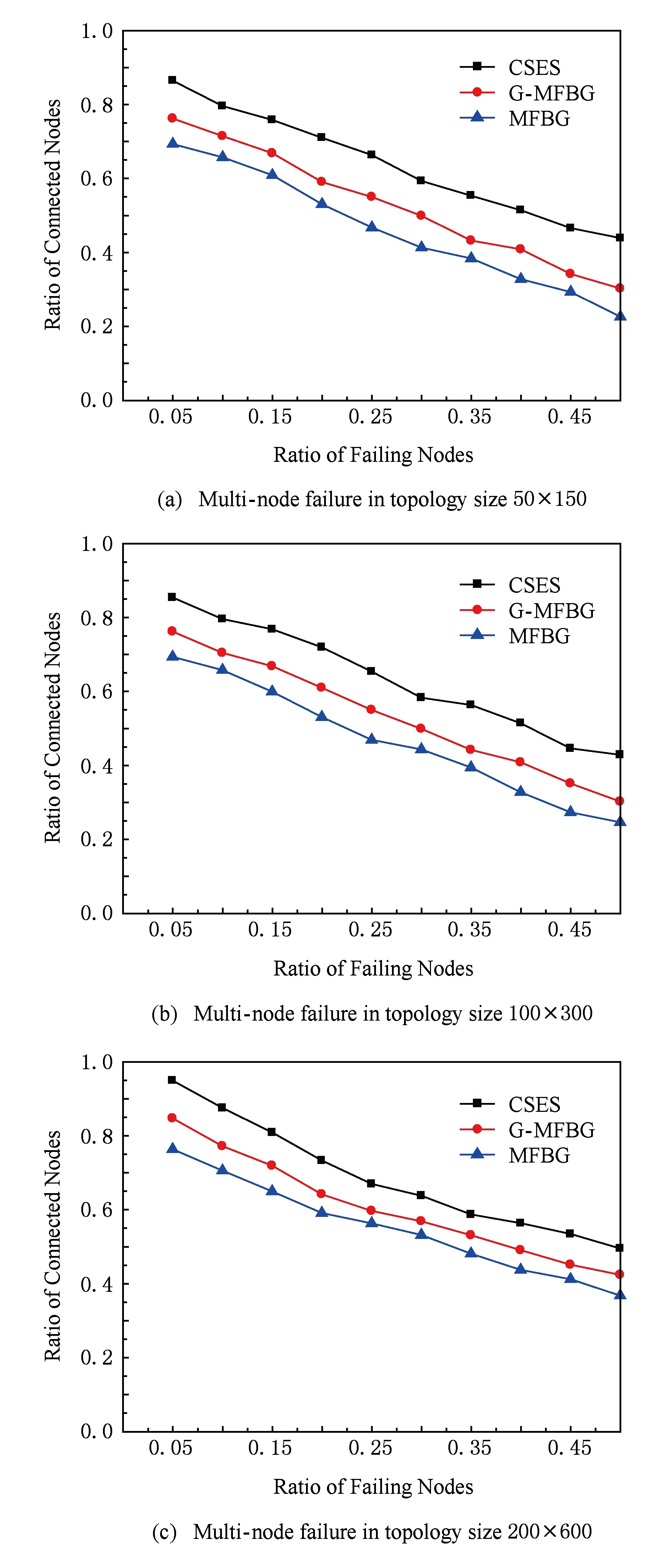
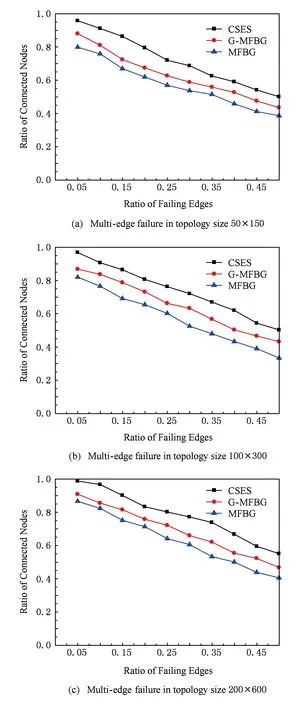
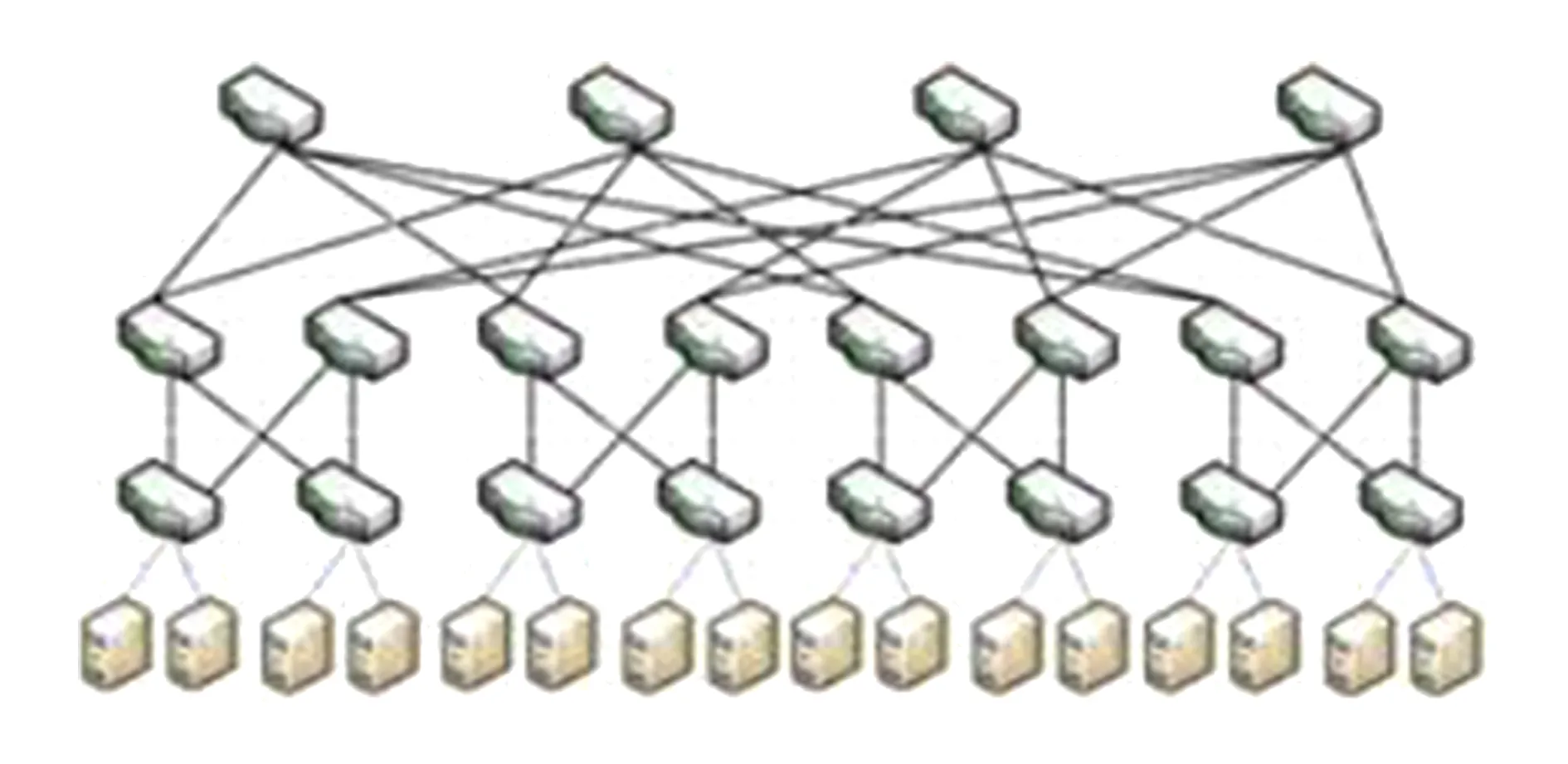
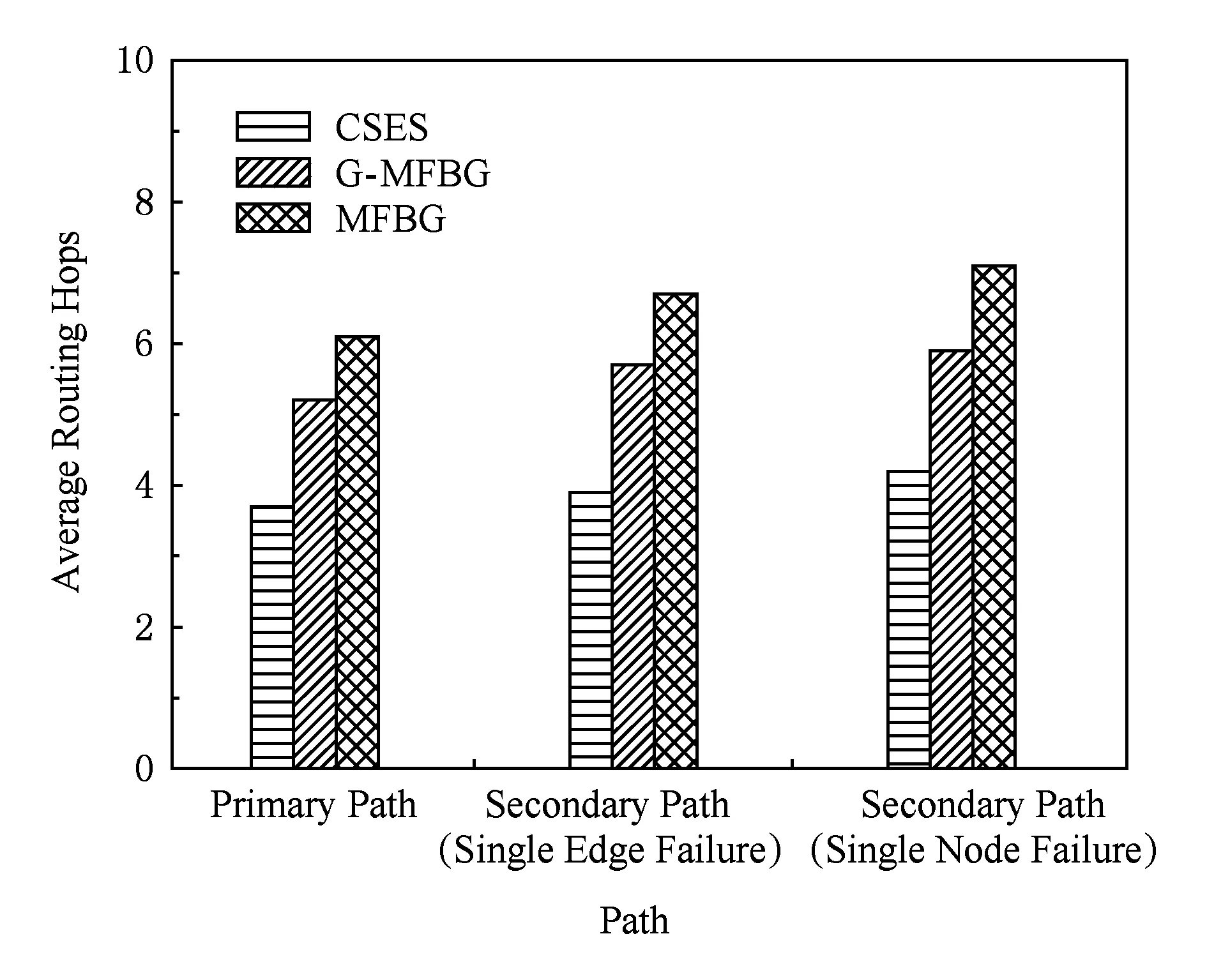
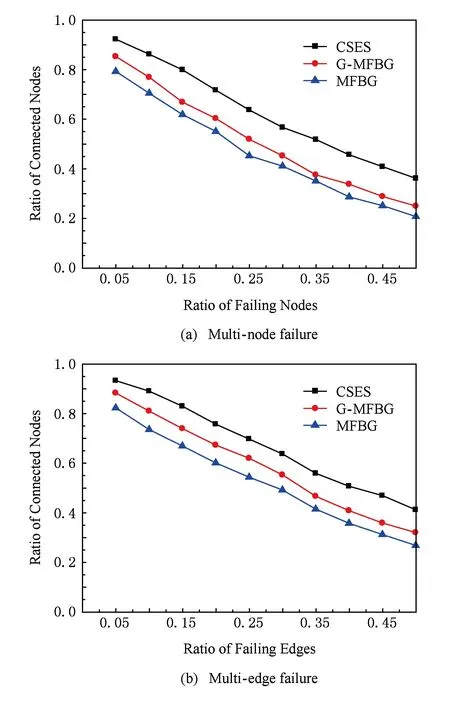
下面对构建冗余树算法的时间复杂度进行分析:设网络拓扑中节点数量为n,边的数量为m,剩余边数量为k(k 1) 针对网络拓扑使用Dijkstra算法生成最小传输树,所需时间复杂度为O(n2); 2) 计算1条剩余边的节点度所需时间复杂度为O(logn),故总的计算节点度的时间复杂度为O(klogn),对剩余边基于节点度由小到大进行排序,所需时间复杂度为O(k2),可知该部分所需时间复杂度为O(klogn+k2); 3) 为每条剩余边在最小传输树上构建相应的环,每次构环的最坏时间复杂度为O(logn),因此总的构环时间复杂度为O(klogn); 4) 在随后的冗余树生成过程中,在最坏情况下每遍历1次剩余边序列只有1个节点加入节点集合T,由于节点集合T初始包含根节点且第1个形成的冗余环至少包含3个节点(其中1个是根节点),可知最多要遍历n-2次剩余边序列,因此冗余树生成部分的最坏时间复杂度为O(kn). 综上所述,整个构建冗余树算法的时间复杂度为O(n2+k2+klogn+kn).作为比较,MFBG算法[13]与G-MFBG算法[18]的时间复杂度分别为O(n2(m+n))和O(n2(m+nlogn)).相比其他算法,本文算法在提升主传输路径以及备份传输路径性能的同时还降低了算法时间复杂度. 下面以图1所示网络拓扑为例,说明构建以A为根节点的冗余树的具体过程: 1) 基于Dijkstra算法生成以A为根节点的最小传输树,如图2所示,并对冗余环节点集合T赋初值T={A}. 2) 根据图1和图2,将剩余边按照边的节点度进行排序,得到的剩余边序列RS如表1所示.随后,按序将剩余边添加到最小传输树上形成相应的环. Table 1 The Sorting Table of Redundant Edge Fig. 5 Selecting (B,C).图5 选取(B,C) 3) 读取剩余边序列中的第1条边(B,C)在最小传输树上形成的环(A,B,C,A),如图5(a)所示.由于该环包含根节点A,可知该环为冗余环.由于边(B,C) 上的2个端点都不属于T,即节点B和节点C都不属于其他冗余环,因此分别向最小传输树上的节点B和节点C添加冗余枝(B,C)和(C,B),并都标上序号1,生成的冗余树如图5(b)所示.随后将环(A,B,C,A)上不在T中的节点B和C加入到T中得到更新后的T={A,B,C},并将边(B,C)从剩余边序列中删除,更新后的剩余边序列如图5(c)所示. 4) 读取更新后的剩余边序列中的第1条边(F,C)在最小传输树上形成的环(A,F,C,A),如图6(a)所示.由于该环包含根节点A,可知该环为冗余环.由于边(F,C)上端点C已经属于T,即节点C已属于其他冗余环,因此只需向最小传输树上的节点C添加冗余枝(C,F)并标上序号2即可,生成的冗余树如图6(b)所示.随后将环(A,F,C,A)上不在T中的节点F加入到T中得到更新后的T={A,B,C,F},并将边(F,C)从剩余边序列中删除,更新后的剩余边序列如图6(c)所示. Fig. 6 Selecting (F,C).图6 选取(F,C) Fig. 7 Selecting (H,F).图7 选取(H,F) 5) 读取更新后的剩余边序列中的第1条边(H,F)在最小传输树上形成的环(A,H,F,A),如图7(a)所示.由于该环包含根节点A,可知该环为冗余环.由于边(H,F)上端点F已经属于T,即节点F已属于其他冗余环,因此只需向最小传输树上的节点F添加冗余枝(F,H)并标上序号3即可,生成的冗余树如图7(b)所示.随后将环(A,H,F,A)上不在T中的节点H加入到T中得到更新后的T={A,B,C,F,H},并将边(H,F)从剩余边序列中删除,更新后的剩余边序列如图7(c)所示. 6) 读取更新后的剩余边序列中的第1条边(B,J)在最小传输树上形成的环(A,B,J,C,A),如图8(a)所示.由于该环包含根节点A,可知该环为冗余环.由于边(B,J)上端点B已经属于T,即节点B已属于其他冗余环,因此只需向最小传输树上的节点B添加冗余枝(B,J)并标上序号4即可,生成的冗余树如图8(b)所示.随后将环(A,B,J,C,A)上不在T中的节点J加入到T中得到更新后的T={A,B,C,F,H,J},并将边(B,J)从剩余边序列中删除,更新后的剩余边序列如图8(c)所示. Fig. 8 Selecting (B,J).图8 选取(B,J) Fig. 9 Selecting (H,G).图9 选取(H,G) 7) 读取更新后的剩余边序列中的第1条边(H,G)在最小传输树上形成的环(A,H,G,F,A),如图9(a)所示.由于该环包含根节点A,可知该环为冗余环.由于边(H,G)上端点H已经属于T,即节点H已属于其他冗余环,因此只需向最小传输树上的节点H添加冗余枝(H,G)并标上序号4即可,生成的冗余树如图9(b)所示.随后将环(A,H,G,F,A)上不在T中的节点G加入到T中得到更新后的T={A,B,C,F,H,J,G},并将边(H,G)从剩余边序列中删除,更新后的剩余边序列如图9(c)所示. 8) 读取更新后的剩余边序列中的第1条边(E,I)在最小传输树上形成的环(B,E,I,B),如图10(a)所示.由于该环上只有1个节点B属于T且不包含根节点A,可知该环不是冗余环,则将边(E,I)搁置,保持冗余树、集合T和剩余边序列均不变,如图10(b)(c)所示. 9) 由于边(E,I)在最小传输树上形成的环不是冗余环,则读取剩余边序列中的下一条边(G,J)与最小传输树所形成的环(A,F,G,J,C,A),如图11(a)所示.由于该环包含根节点A,可知该环为冗余环,然而由于该环上所有节点都已经属于T,说明环上除根节点A之外的所有节点都已存在与根节点A相通的备份路径,则保持冗余树和集合T不变,如图11(b)所示,只需将边(G,J)从剩余边序列中删除即可,更新后的剩余边序列如图11(c)所示. Fig. 11 Selecting (G,J).图11 选取(G,J) 10) 由于边(G,J)在最小传输树上形成的环是冗余环,需要读取更新后的剩余边序列中的第1条边(E,I)与最小传输树所形成的环(B,E,I,B),如图12(a)所示.由于该环上仍然只有1个节点B属于T且不包含根节点A,可知该环不是冗余环,则继续将边(E,I)搁置,保持冗余树、集合T和剩余边序列均不变,如图12(b)(c)所示. Fig. 12 Selecting (E,I).图12 选取(E,I) 11) 由于边(E,I)在最小传输树上形成的环不是冗余环,则读取剩余边序列中的下一条边(D,E)与最小传输树所形成的环(A,C,J,D,E,B,A),如图13(a)所示.由于该环包含根节点A,可知该环为冗余环.由于边(D,E)上的2个节点都不属于T,即节点D和节点E都不属于其他冗余环,因此分别向最小传输树上的节点D和节点E添加冗余枝(D,E)和(E,D),并都标上序号6,生成的冗余树如图13(b)所示.随后将环(A,C,J,D,E,B,A)上不在T中的节点D和节点E加入到T中得到更新后的T={A,B,C,F,H,J,G,D,E},并将边(D,E)从剩余边序列中删除,更新后的剩余边序列如图13(c)所示. Fig. 13 Selecting (D,E).图13 选取(D,E) 12) 读取更新后的剩余边序列中的第1条边(E,I)在最小传输树上形成的环(B,E,I,B),如图14(a)所示.由于此时该环上的节点B和E均已经加入T,因此该环上已经有2个节点属于T,可知该环为冗余环.由于边(E,I)上端点E已经属于T,即节点E已属于其他冗余环,因此只需向最小传输树上的节点E添加冗余枝(E,I)并标上序号7即可,生成的冗余树如图14(b)所示.随后将环(B,E,I,B)上不在T中的节点I加入到T中得到更新后的T={A,B,C,F,H,J,G,D,E,I},并将边(E,I)从剩余边序列中删除,更新后的剩余边序列如图14(c)所示.由于此时有T=V,冗余树构建结束,此时所构建的冗余树即为最终的冗余树,与图3所示冗余树完全相同. Fig. 14 Selecting (E,I).图14 选取(E,I) 为了验证本文提出的CSES算法的效能,使用NS2构建网络仿真环境,使用Java作为开发工具.首先,为与其他冗余树算法进行公平的比较,仿真所需的部分拓扑参照文献[18]所提出的拓扑规模并由拓扑生成器BRITE生成,节点规模分别是50,100,200节点,边的规模分别为3n和nlbn,其中n为节点数.因此可生成6种不同规模的拓扑,可用节点数×边数的形式表示,即拓扑1为50×150,拓扑2为50×250,拓扑3为100×300,拓扑4为100×600,拓扑5为200×600,拓扑6为200×1400.其次,为验证本文算法在数据中心网络拓扑中的有效性,依照文献[5]中所展示的基于Fat-tree的数据中心网络拓扑构建仿真网络拓扑,并依据该拓扑对比本文与其他冗余树算法的效能. 实验1. 比较不同规模拓扑下基于CSES算法、MFBG算法、G-MFBG算法所生成的主传输路径的转发跳数. 首先,分别在6种不同拓扑中随机选择1个节点为数据源节点,使用CSES,MFBG,G-MFBG算法生成传输树;然后计算传输树上根结点到达其他节点的转发跳数的平均值,对上述实验重复50次,结果取平均值.如图15所示,基于CSES算法的传输树具有最小的平均转发跳数;由于MFBG算法在构建传输树时没有考虑到传输路径的转发跳数,随机选环策略导致平均转发跳数较大.尽管G-MFBG算法考虑到路径性能,但是其所得平均转发跳数高于CSES算法所得平均转发跳数,这是因为CSES算法生成的路径具有最小转发跳数. Fig. 15 The comparison of the average forwarding hop count of the primary path.图15 主传输路径平均转发跳数比较 实验2. 比较不同规模拓扑下基于CSES算法、 MFBG算法、G-MFBG算法所生成的备份路径的转发跳数. 首先,比较单边失效后不同算法产生的备份路径的平均转发跳数,对3种算法随机选择相同的1条边令其失效,仿真结果如图16(a)所示.CSES算法所得备份路径的平均转发跳数最少,这是因为该算法采取了基于剩余边节点度排序的选环方法,从而减少了备份路径的平均转发跳数.对于G-MFBG算法,由于其对备份路径的转发跳数没有考虑,故该算法产生的备份路径的平均转发跳数较多.其次,比较单节点失效后不同算法产生的备份路径的平均路由,仍然对3种算法随机选择相同的1个节点(非根节点)令其失效,仿真结果如图16(b)所示.尽管相比单边失效情况下CSES算法所得备份路径的平均转发跳数有所增加,但是CSES算法所得备份路径的平均转发跳数仍然是最少的,这仍然是因为CSES算法为了降低备份路径的转发跳数对剩余边按节点度值进行了排序. Fig. 16 The comparison of the average forwarding hop count of the secondary path in the case of single edgenode failure.图16 单边点失效时备份路径平均转发跳数比较 实验3. 验证在相同拓扑规模和不同节点失效比例下,基于CSES算法、MFBG算法、G-MFBG算法所生成的冗余树抵御多节点失效的能力. 为方便比较,使用在启用备份路径后尚能与根节点保持连接的节点数目与总节点数目的比例(简称连接节点比例)作为度量指标.首先,针对50×150,100×300,200×600这3种拓扑分别设置5%~50%的节点失效率(增长幅度为5%),并通过遍历启用相应冗余枝后的冗余树来计算连接节点比例,分别重复计算50次,最终将所有结果取平均值,实验结果如图17所示.在不同的拓扑中,MFBG算法抵御多节点失效的能力最差,而CSES算法抵御多节点失效能力最好,这是因为CSES算法使用节点度值对剩余边进行排序,从而可生成更多的冗余枝用于构建备份路径. Fig. 17 The comparison of the resistant ability in the case of multiple nodes failure.图17 不同节点失效比例下抵御多节点失效能力 实验4. 验证在相同拓扑规模和不同边失效比例下,基于CSES算法、MFBG算法、G-MFBG算法所生成的冗余树抵御多边失效的能力. 与实验3同样使用节点连接比例作为度量指标,针对50×150,100×300,200×600这3种拓扑分别设置5%~50%的边失效率(增长幅度为5%)并计算连接节点比例,分别重复计算50次,最终将所有结果取平均值,实验结果如图18所示.在不同的拓扑中,相比于多节点失效情况,多边失效情况下各个算法所得出的连接节点比例有所提高,其中,本文CSES算法依旧保持最高的连接节点比例,MFBG算法的抵御多边失效能力最差. Fig. 18 The comparison of the resistant ability in the case of the multiple edges failure.图18 不同边失效比例下抵御多边失效能力 实验5. 在基于Fat-tree的数据中心网络拓扑下验证CSES算法、MFBG算法、G-MFBG算法的效能. 依照文献[5]中所展示的基于Fat-tree的数据中心网络拓扑所构建仿真网络拓扑如图19所示. Fig. 19 The Fat-tree based network topology in data center.图19 基于Fat-tree的数据中心网络拓扑 1) 随机选择1个边界层交换机作为数据源节点,使用CSES,MFBG,G-MFBG算法生成传输树,然后计算传输树上根结点到达其他节点(边界层交换机)的转发跳数的平均值,对上述实验重复50次,结果取平均值,实验结果如图20所示,基于CSES算法的传输树具有最小的平均转发跳数. 2) 比较单边失效后不同算法产生的备份路径的平均转发跳数,对3种算法随机选择拓扑中相同的1条边令其失效,仿真结果如图20所示,CSES算法所得备份路径的平均转发跳数最少. Fig. 20 The comparison of the average forwarding hop count of the primarysecondary path.图20 主备份传输路径的平均转发跳数比较 3) 比较单节点失效后不同算法产生的备份路径的平均路由,在3种算法中随机选择相同的1个节点(非根节点)令其失效,仿真结果如图20所示,尽管相比单边失效情况下CSES算法所得备份路径的平均转发跳数有所增加,但是CSES算法所得备份路径的平均转发跳数仍然是最少的,这是因为CSES算法为了降低备份路径的转发跳数对剩余边按节点度值进行了排序. Fig. 21 The comparison of the resistant ability in the case of multiple nodesedges failure.图21 不同节点失效比例下抵御多节点边失效能力比较 本文提出一种可保障数据无中断传输的按边序选环的冗余树算法.该算法首先基于网络拓扑构建最小传输树,该树上根节点与其他节点之间的转发跳数是最少的.随后,为减少备份路径的转发跳数,本文对剩余边按节点度从小到大进行排序,依次将剩余边添加到最小传输树上构建冗余环,并将冗余环上的冗余枝添加到最小传输树上,最终构建一棵冗余树.实验结果表明,相比于其他冗余树算法,基于本文算法构建的冗余树所生成的主备份路径的转发跳数更少且抵御多节点边失效能力更强. [1]Yi Xiaomeng, Liu Fangming, Liu Jiangchuan, et al. Building a network highway for big data: Architecture and challenges[J]. IEEE Networking, 2014, 3(4): 1-25[2]Li Dan, Chen Guihai, Ren Fengyuan, et al. Data center network research progress and trends[J]. Chinese Journal of Computers, 2014, 37(2): 259-274 (in Chinese)(李丹, 陈贵海, 任丰原, 等. 数据中心网络的研究进展与趋势[J]. 计算机学报, 2014, 37(2): 259-274)[3]Greenberg A, Hamilton J R, Jain N, et al. VL2: A scalable and flexible data center network[C]Proc of the ACM SIGCOMM’09. New York: ACM, 2009: 51-62[4]Niranjan M R, Pamboris A, Farrington N, et al. Portland: A scalable fault-tolerant layer 2 data center network fabric[C]Proc of the ACM SIGCOMM’09. New York: ACM, 2009: 39-50[5]Al-Fares M, Loukissas A, Vahdat A. A scalable, commodity data center network architecture[C]Proc of the ACM SIGCOMM’08. New York: ACM, 2008: 63-74[6]Costa P, Donnelly A, Rowstron A, et al. Camdoop: Exploiting in-network aggregation for big data applications[C]Proc of the 9th USENIX Conf on Networked Systems Design and Implementation. Berkeley, CA: USENIX Association, 2012: 51-75[7]Xiao Bailong, Guo Wei, Liu Jun, et al. Research on local route repair algorithm in mobile ad hoc networks[J]. Journal of Computer Research and Development, 2007, 44(8): 1383-1389 (in Chinese)(肖百龙, 郭伟, 刘军,等. 移动自组网路由局部修复算法的研究[J]. 计算机研究与发展, 2007, 44(8): 1383-1389)[8]Zhang Li, Li Jinbao. Multi-Path based reliable routing in wireless sensor network[J]. Journal of Computer Research and Development, 2011, 48(Suppl 2): 171-175 (in Chinese)(张莉, 李金宝. 无线传感器网络中基于多路径的可靠路由协议研[J]. 计算机研究与发展, 2011, 48(增刊2): 171-175)[9]Challal Y, Ouadjaout A, Lasla N, et al. Secure and efficient disjoint multipath construction for fault tolerant routing in wireless sensor networks[J]. Journal of Network and Computer Applications, 2011, 34(4): 1380-1397[10]Xu M, Hou M, Wang D, et al. An efficient critical protection scheme for intra-domain routing using link characteristics[J]. Computer Networks, 2013, 57(1): 117-133[11]Suchara M, Xu D, Doverspike R, et al. Network architecture for joint failure recovery and traffic engineering[C]Proc of the ACM Sigmetrics (SIGMETRICS’11). New York: ACM, 2011: 97-108[12]Su Jinshu, Hu Qiaolin, Zhao Baokang. Disruption-free forwarding survivable routing protocols on Internet[J]. Journal of Software, 2010, 21(7): 1589-1604 (in Chinese)(苏金树, 胡乔林, 赵宝康. 互联网无中断转发的生存性路由协议[J]. 软件学报, 2010, 21(7): 1589-1604)[13]Médard M, Finn S G, Barry R A, et al. Redundant trees for preplanned recovery in arbitrary vertex redundant or edge redundant graphs[J]. IEEEACM Trans on Networking, 1999, 7(5): 641-652[14]Aun H, Richard H. Recovery techniques in next generation networks[J]. IEEE Communications Surveys & Tutorials, 2007, 9(3): 2-17[15]Jayavelu G, Ramasubramanian S, Younis O. Maintaining colored trees for disjoint multipath routing under node failures[J]. IEEEACM Trans on Networking, 2009, 17(1): 346-359[16]Cho S, Elhourani T, Ramasubramanian S. Independent directed acyclic graphs for resilient multipath routing[J]. IEEEACM Trans on Networking, 2012, 20(1): 153-162[17]Yong O L, Narasimha R. Constructing disjoint paths for failure recovery and multipath routing[J]. Computer Networks, 2012, 56(2): 719-730[18]Xue G, Chen L, Thulasiraman K. Quality-of-service and quality-of-protection issues in preplanned recovery schemes using redundant trees[J]. Journal on Selected Areas in Communications, 2003, 21(8): 1332-1345[19]Wu K, Xiao J, Ni L M. Rethinking the architecture design of data center networks[J]. Frontiers of Computer Science, 2012, 6(5): 596-603[20]Rojas E, Ibanez G, Gimenez-Guzman J M, et al. All-Path bridging: Path exploration protocols for data center and campus networks[J]. Computer Networks, 2015,79(14): 120-132 Xia Nu, born in 1981. PhD candidate. His main research interests include network management. Li Wei, born in 1978. Associate professor and master supervisor. Member of China Computer Federation. His main research interests include next generation network architecture and service computing. Lu You, born in 1977. PhD candidate. Member of China Computer Federation. His main research interests include network management. Jiang Jian, born in 1986. PhD candidate. His main research interests include network management. Shan Feng, born in 1985. PhD candidate. His main research interests include wireless sensor network and algorithm design. Luo Junzhou, born in 1960. Professor and PhD supervisor. Senior member of China Computer Federation. His main research interests include next generation network architecture, protocol engineering, network security, wireless network and cloud computing. The Redundant Tree Algorithm for Uninterrupted Data Delivery Xia Nu, Li Wei, Lu You, Jiang Jian, Shan Feng, and Luo Junzhou (SchoolofComputerScience&Engineering,SoutheastUniversity,Nanjing211189) With the development of the big data applications, the requirement for guaranteeing un-interrupted data delivery is growing gradually. To address the problem of single nodelink failure, researchers had conducted lots of work. However, current methods for guaranteeing uninterrupted data delivery face the deficiencies of low performance of the primarysecondary delivery paths and the low resistant ability to the multiple nodeslinks failure. In order to solve the above problems, a circle selecting by edge sorting based redundant tree algorithm for uninterrupted data delivery CSES is presented. At first, a minimal delivery tree with the data source as the root node is built in this algorithm, on which the routing hop count of the primary paths is the smallest. Secondly, in order to reduce the hop count of the secondary paths and to enhance the resistant ability of the multiple nodesedges failure, the edges in network topology but not included in the tree are sorted based on the sum of the nodes on the paths between the root node and the two nodes of the edge. Then, the edges are added to the minimal tree to form the redundant circles and the redundant branches of the redundant circles are added to the minimal tree. Finally, a redundant tree rooted by the data source is built. The experimental results show that, compared with the other redundant tree algorithms, the hop count of the primarysecondary paths on the redundant tree built by CSES algorithm is smaller and the resistant ability of multiple nodesedges failure of CSES algorithm is better. the uninterrupted data delivery; the minimal delivery tree; edge sorting; the redundant circle; the redundant tree 2015-05-21; 2015-10-29 国家自然科学基金项目(61320106007);国家“八六三”高技术研究发展计划基金项目(2013AA013503);江苏省未来网络创新研究院未来网络前瞻性研究项目(BY2013095-2-07);教育部计算机网络与信息集成重点实验室(东南大学)基金项目(93K-9);江苏省网络与信息安全重点实验室基金项目(BM2003201);无线通信技术协同创新中心资助项目;软件新技术与产业化协同创新中心部分资助项目;住建部科研项目(2015-K6-012) This work was supported by the National Natural Science Foundation of China (61320106007), the National High Technology Research and Development Program of China (863 Program) (2013AA013503), the Prospective Research Project on Future Networks of Jiangsu Future Networks Innovation Institute (BY2013095-2-07), the Project Funded by Key Laboratory of Computer Network and Information Integration (Southeast University) of Ministry of Education of China (93K-9), the Project Funded by Jiangsu Provincial Key Laboratory of Network and Information Security (BM2003201), the Project Funded by Collaborative Innovation Center of Wireless Communication Technology, the Project Funded by Collaborative Innovation Center of Novel Software Technology and Industrialization, and the Project Funded by Ministry of Housing and Urban-Rural Development (2015-K6-012). TP391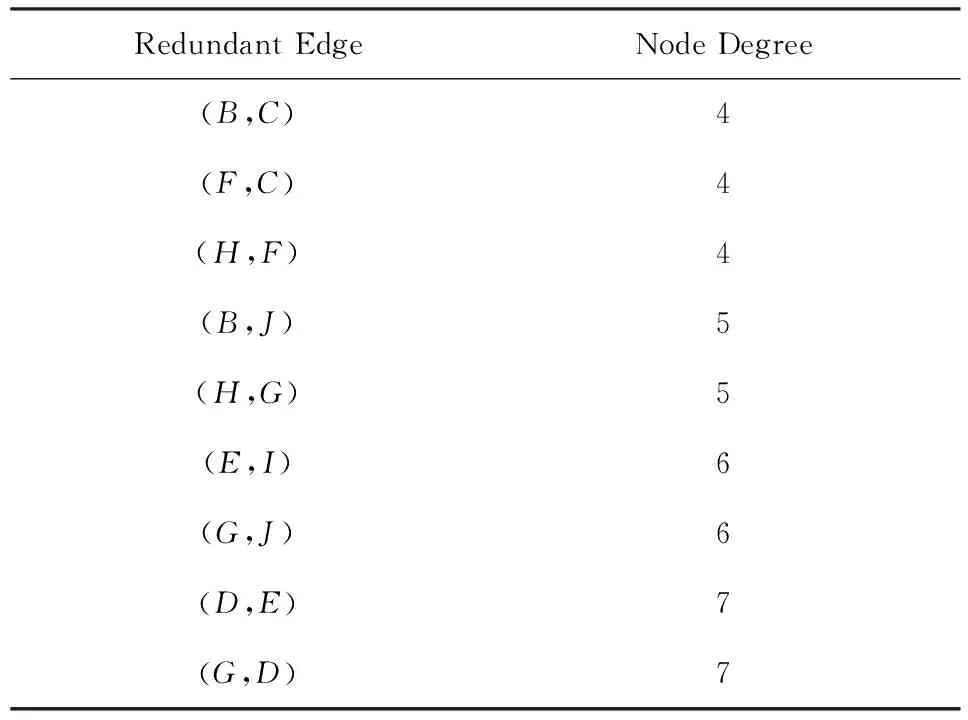

4 实 验
5 结束语






