指数均值回复金融市场下的最优投资和最优再保险策略

李启才，顾孟迪



指数均值回复金融市场下的最优投资和最优再保险策略

李启才1，顾孟迪2

（1.南京师范大学数学科学学院, 江苏南京 210023; 2.上海交通大学安泰经济与管理学院, 上海 200052）

近来，随机控制理论广泛应用于精算数学领域。这是因为保险公司的资产管理越来越技术化。保险公司可以通过购买再保险来控制和转移它们的风险，通过投资金融市场来管理它们的利润。为了更好的利用这些机会，它们需要随机控制的技巧。本文利用带有漂移的布朗运动描述索赔过程，在终端指数效用最大化的目标下，考虑保险公司的最优再保险和投资决策。文章假定保险公司投资于指数均值回复的金融市场。同时保险公司通过购买一个纯比例或者纯超额损失亦或是二者组合的再保险来转移索赔风险。利用随机控制理论，获得了值函数、最优再保险和投资策略的表达式。最优投资策略中第一项类似经典Merton策略：投资风险资产资金与单位风险溢价成正比。第二和第三项则分别是根据资产价格和时间对投资行为的调整。文章也证明了最优的再保险策略是购买一个纯的超额损失再保险，而非纯比例或组合再保险，从而也说明超额损失再保险总是优于比例再保险。最后给出了一些数值例子。

随机控制；再保险；指数均值回复；效用函数

0 引言

投资和再保险已成为现代保险公司越来越倚重的增加收益和管理风险的有效工具。近年来，大量文献讨论了保险公司在Black-Scholes（B-S）金融市场中的最优再保险和最优投资问题。这些工作中，以破产概率最小化或终端财富效用最大化等为目标，运用随机控制理论和相关方法得到保险公司的最优策略和值函数。例如Browne[1]利用带有漂移的布朗运动描述保险公司的盈余过程，得到了最大化终端时刻财富的期望指数效用下的最优投资策略。Schmidli[2]，Taksar 和 Markussen[3]研究了最小化破产概率下保险公司的最优比例再保险策略。Luo et al.[4]考虑了最小化破产概率下的最优投资和比例再保险策略。Bai 和Guo[5]分析了最大化终端财富指数效用下，保险公司的最优投资和比例再保险策略。另外，Irgens 和 Paulsen[6]考虑了跳-扩散金融市场下的最优投资和比例再保险问题，得到了最优策略和值函数的近似表达式。Liang et al.[7]研究了资产收益率服从一般Ornstein－Uhlenbeck过程下的最优投资和比例再保险策略。Gu et al.[8]和Liang et al.[9]分别研究了扩散索赔和跳-扩散索赔情形的常弹性方差（CEV）模型下的最优投资和比例再保险问题，得到了相关最优策略和值函数的（近似）表达式。荣喜民和范立鑫[10]也考虑了常弹性方差(CEV)模型下保险公司的最优投资策略。

事实上，在一个均衡的环境中，若资产价格相对偏高，人们将预期供给上升并对价格产生一个向下的压力；反过来说，若价格偏低，供给会减少并对价格产生一个向上的压力，即产生所谓的均值回复现象。Schwartz[11]实证了指数均值回复过程（Exponential mean-reversion）描述资产价格均值回复特性的合理性，提出了著名的Schwartz指数均值回复模型。Schwartz指数均值回复过程可以广泛用来描述商品期货、债券、股票或利率等的相关金融资产的动态价格。Benth 和Karlsen[12]以最大化终端财富期望幂效用为目标，在风险资产的价格服从Schwartz模型的假设下，研究了经典默顿问题。王蕾和顾孟迪[13]研究了Schwartz模型下的比例再保险和投资问题。与文献[13]不同的是，本文研究Schwartz 模型下比例－超额损失组合再保险和投资问题。这类再保险形式更全面，应用上更广泛，但数学上求解却更复杂：因为比例再保险是线性的，而超额损失再保险是非线性的。于是，经过购买超额损失（或比例－超额损失组合）再保险后的保险公司自留风险的期望和方差表达式都更加复杂（详见下文1.1）。

多数再保险文献都是考虑保险公司要么购买一个纯比例再保险，要么购买一个纯超额损失再保险[2-9]，本文考虑的组合形式再保险的相关综述工作，可以参见Centeno[14]。另外，Zhang et al.[15]和Zhou et al.[16]分别研究了最小破产概率和VaR （Value at Risk）准则下的比例-超额损失组合再保险策略，它们都得出纯超额损失策略更好的结论。Liang 和Guo[17]在效用最大化准则下，研究了比例－超额损失组合再保险策略，他们断言在单次索赔的预期最大值足够大时应该采取纯超额损失再保险，反之，应该采用纯比例策略。但[17]没有专门讨论比例再保险情形。事实上，本文通过计算得出结论，最优的组合再保险策略实际上等同于最优纯超额损失再保险策略。从而也说明了超额损失再保险总是优于比例再保险。但本文的优化目标和证明方法都不同于文献[15][16]。另外，以上讨论组合再保险的工作中，都没有涉及到金融市场的投资，本文得到Schwartz指数均值回复金融市场下的保险公司最优投资策略。实务中，对保险公司的索赔量分布，自身的风险厌恶系数及再保险公司的保费率的估计非常重要，本文最后部分给出了相关参数对最优策略影响的一些数值演示。

1 模型和动态规划方程

1.1 再保险－投资模型

在经典的风险模型（Cramér-Lundberg），盈余过程可以描述为

， （2）

考虑保险公司通过购买下列形式的比例－超额损失组合形式再保险来转移它们面临的索赔风险。设表示保险公司在时刻的比例再保险自留比例，而为保险公司在时刻的超额损失再保险自留额。为简洁起见，记再保险决策变量为。购买组合（excess-of-loss after quota-share）再保险后，保险公司每次索赔的自留额变成，而部分由再保险公司支付，。于是保险公司的盈余过程变为

，（4）

同时，保险公司可以在金融市场中投资某项风险资产。如前所述，由于Schwartz 指数均值回复过程更接近现实。故假定风险资产的价格如下：

.

又设无风险资产价格为

。 （8）

1.2 动态规划方程

相应的值函数为

（10）

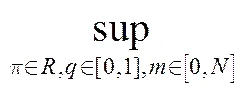
其边界条件为

， （12）

其中微分算子

下列验证定理保证了满足边界条件（12）的方程（11）的经典解确实是我们问题所需要的值函数，其相关证明见Fleming 和Sonner[19]。

2 模型求解

指数效用常用于保险数学与精算实践，它具有常数绝对风险厌恶（constant absolute risk aversion(CARA)）参数，是在“零效用” 原理下唯一得出独立于保险公司盈余水平的公平保费的函数[17]。因此，本文设保险公司具有下列指数效用

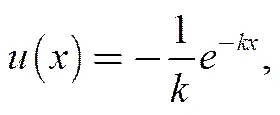
为求解方程（11），受Brown[1]启发，猜想值函数有下列形式解

边界条件为

（15）

，（17）

， （20）

也就是说，此时应该采用一个最优的纯超额损失再保险策略。

。（24）

（25）

， （27）

， （28）

结合（24）式中的边界条件，容易解出，

， （30）

， （31）

定理2.2 定理2.1条件下的最优投资策略和值函数分别为

。（33）

注2.2最优投资策略第一项类似经典Merton[20]投资策略：它与单位风险溢价成正比，其中比例因子与风险厌恶参数有关。而第二和第三项是根据资产价格和时间对投资策略的调整。从策略表达式容易看出，如果是多头，风险厌恶参数越大或资产价格波动越大，都会导致较低的风险资产投资额。至于是多头还是空头，主要依赖于资产价格（或其对数）的变化。

其中

，

其中

，（18’）

定理2.4纯超额损失再保险总是优于文中形式的比例-超额损失组合再保险，也优于比例再保险。

注2.3 定理2.4的结论类似Zhang et al.在破产概率最小化下得到的结论（文[14] 中Theroem 2.1），本文在效用最大化准则下，采用了一种不同于他们的计算式证明。定理2.4说明在期望值保费原理下，本文的组合最优再保险策略等同于纯超额损失再保险策略，保险公司不会购买比例再保险，也不会购买比例－超额损失组合形式的再保险。

3 最优策略数值分析

为了更加直观地解释最优投资和再保险策略，我们给出一些在数值图形。设定，，，不变。假定股票初始价格，均值回复速率，利用的解，模拟产生一条样本路径（），带入相应的最优策略表达式，得到图1中所示的一条样本路径（散点）图。该样本路径图显示时，投资人在风险资产上处于空头投位置，而其它时间点投资人则是多头的。

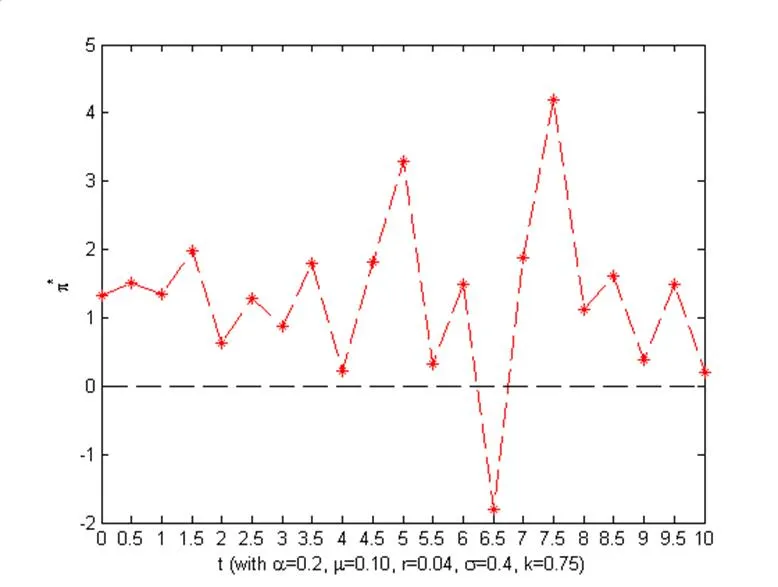
图1 最优投资策略的一条样本路径()

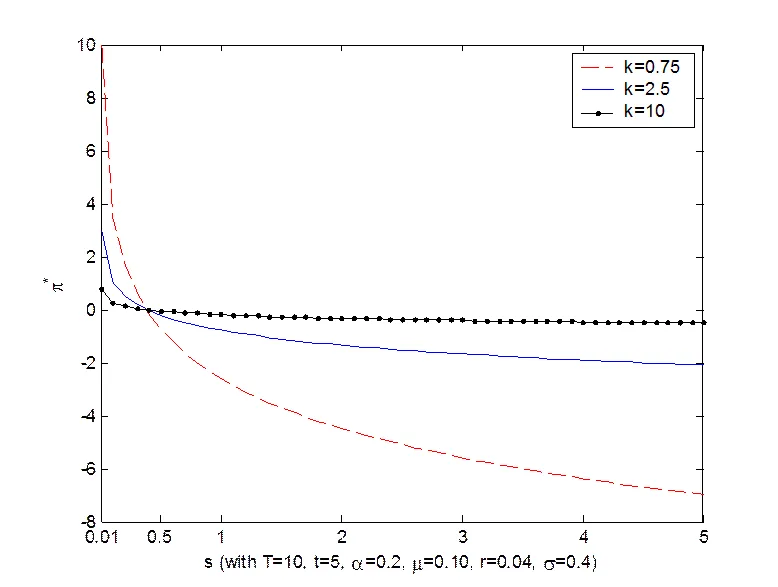
图2 股价对最优投资策略的影响

图3 均值回复速率对最优投资策略的影响

图4 最优超额损失再保险策略

4 结论与展望

本文考虑了保险公司购买比例－超额损失组合形式的再保险，同时投资于指数均值回复金融市场下的最优动态策略。通过随机控制理论，在最大化指数效用准下，我们得到了最优的投资策略由三项和得到：第一项与资产的单位风险溢价成正比，其中比例因子与风险厌恶参数有关，而第二和第三项是根据资产价格和时间对投资策略的调整。而最优的再保险策略则是保险公司总是倾向选择一个最优的超额损失再保险策略，自留的超额损失额或者是全部自留，或者是再保险公司安全载荷系数的某种形式上的“折现”。注意到文中再保费率使用的都是期望值原理，同时组合形式也限于先比例再超额损失，如果采用其他保费原理（如方差保费原理，指数保费原理等），或是其它组合形式（例如自留额为的组合形式），那么结论未必成立。另外对于金融市场可能更复杂，比如回报率和波动率都是随机的等情形，今后将进一步研究这些类型的再保险和投资问题。

[1] Browne S. Optimal investment policies for a firm with random risk process: exponential utility and minimizing the probability of ruin[J]. Mathematics of Operations Research, 1995, 20(4): 937-958.

[2] Schmidli H. Optimal proportional reinsurance policies in a dynamic setting[J]. Scandin- avian Actuarial Journal, 2001, 1:55-68.

[3] Taksar, M., Markussen C. Optimal dynamic reinsurance policies for large insurance portfolios[J]. Finance and Stochastics, 2003 , 7: 97-121.

[4] Luo S, Taksar M, Tsoi A. On reinsurance and investment for large insurance portfolios[J]. Insurance: Mathematics and Economics, 2008, 42:434-444.

[5] Bai L, Guo J. Optimal proportional reinsurance and investment with multiple risky assets and no-shorting constraint [J]. Insurance: Mathematics and Economics, 2008, 42:968-975.

[6] Irgens C, Paulsen J. Optimal control of risk exposure, reinsurance and investment for insurance portfolios[J]. Insurance: Mathematics and Economics, 2004, 35:21-51.

[7] Liang Z, Yuen KC, Guo, J. Optimal proportional reinsurance and investment in a stock market with Ornstein-Uhlenbeck Process[J]. Insurance: Mathematics and Economics, 2011, DOI:10.1016/j.insmatheco.2011.04.005.

[8] Gu M, Yang P, Li S,. Constant elasticity of variance model for proportional reinsurance and investment strategies[J]. Insurance: Mathematics and Economics, 2010, 46:580-587.

[9] Liang Z, Yuen KC, Cheung KC. Optimal reinsurance-investment problem in a constant elasticity of variance stock market for jump-diffusion risk model[J]. Applied Stochastic Models in Business and Industry, 2011, DOI:10.1002/ASMB.943.

[10] 荣喜民, 范立鑫. 常弹性方差模型下保险人的最优投资策略[J]. 系统工程理论与实践，2012, No.12 2619-2628.

[11] Schwartz ES. The stochastic behaviour of commodity prices: Implications for valuation and hedging[J]. J. Finance, 1997, LII(3):923-973.

[12] Benth FE. , Karlsen KH. A note on Merton’s portfolio selection problem for the Schwartz mean-reversion model[J]. Stochastic Analysis and Applications, 23(4)687-704.

[13] 王蕾, 顾孟迪. 均值回复市场中的最优再保险和投资决策[J]. 上海交通大学学报(自然科学版),2013, No.3 438-443.

[14] Centeno L. On combining quota-share and excess-of –loss[J]. ASTIN Bulletin, 1985,15(1):49-63.

[15] Zhang X, Zhou M, Guo J. Optimal combinational quota-share and excess-of-loss reinsurance policies in a dynamic setting[J]. Appl. Stochastic Models Bus. Ind., 2007,23:63-47.

[16] Zhou M, Dong H, Xu J. Optimal combinational of quota-share and stop-loss reinsurance contracts under VAR and CTE with a constrained reinsurance premium[J], J Syst Sci Complex,2011 24:156-166.

[17] Liang Z, Guo J. Optimal combining quota-share and excess of loss reinsurance to maximize the expected utility[J], J Appl Math Comput,2011 36:11-25.

[18] Grandell J. Aspects of Risk Theory[M]. NewYork: Springer-Verlag, 1991.

[19] Fleming W, Soner H. Controlled Markov Process an Viscosity Solutions (Second Edition) [M]. New York: Spring, 2005.

[20] Merton RC. Life portfolio selection under uncertainty: the continuous-time case[J]. The Review of Economics and Statistics,1969, LI:247-257.

Optimal Reinsurance and Investment Policies under Exponential Mean-Reversion Financial Market

LI Qi-cai1, GU Meng-di2

（1. School of Mathematical Sciences, Nanjing Normal University, Nanjing 210023, China;2. Antai College of Economics and Management, Shanghai JiaoTong University, Shanghai 200052, China)

There has been an increasing interest in the use of stochastic optimal control theory in actuarial mathematics. This is due to the fact nowadays the asset-liability management of insurance companies is becoming more and more technical and increasing intertwined with the financial sector. Major insurance companies have opportunity to invest part of their reserves into financial market and take reinsurance to manage and control their exposure to risk. In order to make the best use of these opportunities, they need the techniques of optimal control.

In this paper, claim risk process was modeled by Brownian motion with drift, and the optimization problem was studied of maximizing the exponential utility of terminal wealth under the controls of combining quota-share and excess-of-loss reinsurance and investment. we consider the insurer invests its wealth in exponential mean-reversion stock market. And, the insurer has a choice of reinsuring his claim risk either by a pure quota-share treaty, or by a pure excess of loss treaty or by any combination of the two.

Using stochastic control theory , explicit expressions for the optimal polices and value function are obtained. The first term of optimal investment strategy is analogous to the classical Merton investment policy，which says that it is optimal to invest a fraction in the risky asset proportional to the risk premium per unit risk. The second and the third term of investment strategy adjust the investment behavior according to price level of asset and time respectively. We also show that the optimal excess-of-loss reinsurance is always better than combining quota-share and excess -of-loss reinsurance. And some numerical examples are given.

stochastic control; reinsurance; exponential mean-reversion; utility function

中文编辑：杜 健；英文编辑：Charlie C. Chen

F 830.91

A

1004-6062(2016)04-0079-06

10.13587/j.cnki.jieem.2016.04.010

2013-06-24

2014-5-05-26

国家自然科学基金资助项目 (61304065, 11471165 )；南京师范大学青蓝工程项目

李启才(1979—)，男，安徽东至人；南京师范大学，副教授。研究方向：随机控制理论及其应用。