扩散风险模型下保险公司和再保险公司之间的最优再保险策略选择博弈

林 祥, 朱冠霞, 钱艺平

(浙江工商大学金融学院，杭州 310018)

0 引言

再保险合约是在原保险合约上的保险合约，是再保险公司与保险公司之间的保险合约，是保险公司分散经营风险，控制保险责任，扩大承保能力的重要手段。保险公司是与投保人签订保险合约的保险人，再保险公司是与保险公司签订分保合同的保险人。当投保人与保险公司签订保险合约，保险合约的期望收益已经确定。因此，在保险公司向再保险公司购买再保险时，在承担风险和获得收益之间有一个替换，存在着价格和需求之间的一个博弈。若再保险价格太高，保险公司将购买少量的再保险或者不购买再保险，自己承担风险，获得收益。若再保险价格太低，则再保险公司不愿意提供再保险合约。

Borch[1]研究了两家保险公司通过谈判达成一个互惠再保险合约问题，利用博弈理论得到两家保险公司合作对策的互惠再保险合约。Borch[2]和Arrow[3]给出了再保险市场模型和市场均衡的价格，但这是一个静态模型。随后，有大量的文献研究了使得期望终端财富效用最大化或破产概率最小化的最优再保险策略选择问题，具体见文献[4–10]。也有大量文献研究在各种风险测度下的最优再保险问题，Cai 和Tan[11]使用保险公司总成本的在险价值(VaR)和条件期望尾部值(CTE)作为最优化目标，得到停止损失再保险的最优自留额。Chi 和Tan[12]通过对保险公司在VaR 和条件在险价值(CVaR)标准下的总风险暴露最小化，研究了两类最优再保险模型。Zhou 等[13]通过控制定额分担和停止损失再保险策略，考虑了使得保险公司自留风险的VaR 和CTE 测度最小化问题。Cui 等[14]在一般保费原理下，利用扭曲测度研究了保险公司的最优再保险问题，得到最优再保险策略的显示解。Bensoussan 等[15]、Pun 和Wong[16]、Chen 等[17]、Deng 等[18]研 究 两 个 竞 争 保 险 公司之间的非零和再保险和投资随机微分博弈问题。但这些文献都站在保险公司的角度，仅仅考虑保险公司的最优再保险策略选择。

也有一些文献从再保险公司的角度，研究再保费定价和最优再保险合约设计问题。Suijs 等[19]把再保险策略选择问题转化成保险公司和再保险公司之间的具有随机损益的合作博弈问题。Jean-Baptiste 和Santomero[20]考虑了非对称信息下保险者和再保险者通过再保险分散风险问题，得到信息对风险承担和再保险保费定价的影响。Zeng 和Luo[21]通过把再保险转化为连续时间随机合作博弈问题，利用随机控制原理得到Pareto 最优再保险策略为停止损失再保险或比例再保险，依赖于保费原理的选择。Boonen 等[22]研究了再保险合约的价格，与无差别定价相比，保险者和再保险者通过讨价还价，从再保险中获得收益。Hu 等[23]在保险者或再保险者索赔过程模型不确定下，从委托-代理框架考虑了连续时间再保险合约设计问题，得到最优再保险合约的显示表达式。王愫新等[24]同时考虑保险公司和再保险公司的最优再保险和投资问题，且风险资产的价格服从Heston 随机方差模型，在保险公司和再保险公司终端期望财富效用最大化目标下，得到了保险公司和再保险公司的最优再保险和投资策略，以及值函数的显示表达式。王愫新和荣喜民[25]用带漂移项的布朗运动来描述赔付过程，保险公司可以向再保险公司购买比例再保险，并都能投资于金融市场，得到保险公司的最优分保和投资策略，以及再保险公司的最优承保和投资策略的显示解。Chen 和Shen[26]在期望财富效用最大化下，考虑了保险公司和再保险公司之间的随机leader-follower 比例再保险博弈问题，在指数效用函数下，得到了再保险公司的最优再保费，保险公司的最优自留额，以及保险公司和再保险公司值函数的显示表达式。Hu 等[27]在再保险公司索赔强度不确定下，从委托-代理框架考虑了连续时间比例再保险和停止损失再保险合约选择问题，在指数效用函数下，得到最优再保险合约的显示表达式。

在实际再保险市场，保险公司可以选择分保或不分保，同时，再保险公司也可以承保或不承保，以及承保的数量，保险公司和再保险公司关于再保险之间存在着一个博弈。对比已有文献的研究，本文的贡献主要体现在以下三个方面。首先，本文在同时考虑保险公司和再保险公司利益条件下，根据博弈主导者的不同建立了保险公司和再保险公司之间的三种再保险策略选择博弈模型。现有文献对再保险合约的研究，要么站在保险公司的角度，要么站在再保险公司的角度，或仅仅考虑保险公司和再保险公司共同主导情形。其次，在保险公司和再保险公司都具有指数效用下，得到了三种博弈情形下比例再保险合约能够成交的条件。这些新的结果对保险公司购买再保险和再保险公司承保有重要的指导意义，同时也为再保险合约设计提供参考。最后，分析了再保险合约，以及保险公司和再保险公司的效用损益与模型主要参数之间的关系。现有文献并没有考虑效用损益与模型主要参数之间的关系，这些结果有助于更好地理解再保险合约的选择和设计，完善再保险策略选择理论。

1 模型

1.1 盈余过程

为了更好地理解扩散风险模型，首先给出经典的Cramer-Lundberg 风险模型

假设保险公司通过购买再保险来控制自己的风险水平，对每一次赔付，假设保险公司购买的比例再保险水平为1−a，其中a称为风险暴露，即为保险公司的自留风险比例。同时保险公司要支付部分保费给再保险公司，假设η为再保险公司所要求的单位时间的保费收入，则再保险保费为(1−a)η，且η ≥µ。在保险公司自留比例为a时，保险公司的盈余过程为

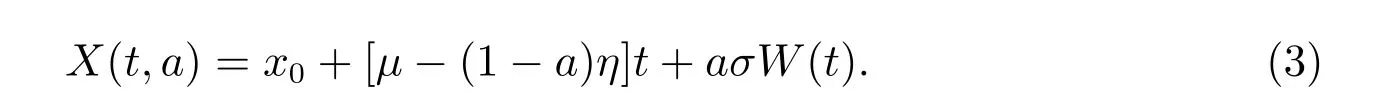
如果自留额a满足0≤a ≤1，则称a是可行再保险策略。所有的可行再保险策略组成的集合记为Π1。假设再保险公司自身并没有参与其它的保险活动，其收入来源完全由再保险保费构成，则再保险公司承保后的盈余过程为

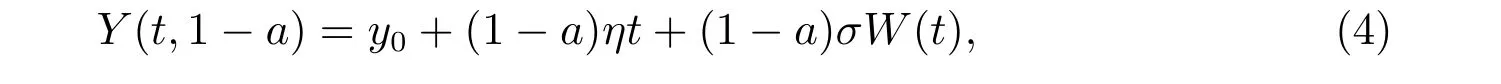
其中y0≥0 是再保险公司的初始盈余，(1−a)为再保险公司的分入比例。如果分入比例1−a满足0≤1−a ≤1，则称1−a是可行分入策略。所有的可行分入策略组成的集合记为Π2。

1.2 目标函数

若保险公司不分保，则保险公司在T时刻的期望盈余效用为

在实际再保险市场，保险公司可以选择分保或不分保，同时，再保险公司也可以承保或不承保，以及承保的数量，保险公司和再保险公司之间关于再保险存在着一个博弈。假设保险公司以期望盈余效用增加作为分保的条件，再保险公司也以期望盈余效用增加作为承保的依据。一个合理的再保险合约应该同时考虑保险公司和再保险公司的利益，双方的期望终端盈余效用都要增加，再保险合约才能成交。由于保险公司和再保险公司所处主体地位的不同，需要考虑谁是博弈的主导者，故对应以下三种情形：

(i) 保险公司占主导。保险公司决定再保险保费和购买比例再保险的数量，再保险公司只能根据再保险保费决定是否承保此数量再保险。保险公司选择可行比例再保险策略a∗，使得

保险公司决定购买此再保险时再保费应满足

如果保险公司和再保险公司具有一般的效用函数，那么要判断三种博弈情形下解的存在唯一性是比较困难的，即使三种博弈情形下存在解，要得到其解的显示表达式也是十分困难的。

2 CARA 效用保险公司和再保险公司

2.1 保险公司占主导

下面，在保险公司占主导下，考虑保险公司的最优比例再保险策略和再保险公司的承保条件。

推论1 如果再保费满足η<α1σ2，则有V1(t,x)> ¯V1(t,x)，即保险公司选择最优比例再保险策略能够提高保险公司的期望盈余效用。

证明 由(17)和(20)，可得

2.2 保险公司和再保险公司共同主导

下面，在保险公司决定购买再保险比例，再保险公司决定再保费下，考虑再保险公司的最优再保费和保险公司的最优再保险策略。

定理3 在指数效用函数下，保险公司的最优比例再保险策略为

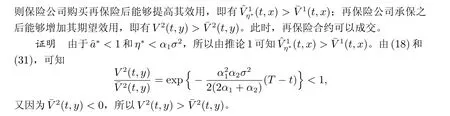
2.3 再保险公司占主导

下面，在再保险公司占主导，考虑再保险公司的最优承保比例和保险公司购买该再保险的条件。

定理4 假设再保险公司具有指数效用函数，则再保险公司的最优承保比例为

注2 在三种博弈情形下，我们得到的最优再保险策略和再保费都是常数，但特别注意最优再保险策略和再保费都是依赖于索赔大小和索赔强度，这是基本符合实际的。因为没有考虑投资，所以最优再保险策略是常数，不随时间的变化而变化。不考虑投资，是因为单独考虑再保险有利于更好地探讨在不同的情形下再保险合约能够成交的条件，以及再保险合约对保险公司和再保险公司效用损益的影响。

3 结果比较与灵敏性分析

下面分别考虑三种博弈情况下最优再保险合约与模型主要参数之间的关系，并通过数值计算得到保险公司和再保险公司的效用损益与模型主要参数之间的关系。

由于V1(t,x)<0 和¯V1(t,x)<0，定义

为保险公司购买再保险后对应的效用损益。若L1(T)> 0，则表示保险公司购买再保险后终端期望盈余效用会增加，即保险公司有效用收益，L1(T)的大小为保险公司效用增加百分比；L1(T)< 0 表示保险公司购买再保险后终端期望盈余效用会减少，即保险公司有效用损失，L1(T)的大小为保险公司效用损失百分比。同样的，定义

为再保险公司选择承保后对应的效用损益。若L2(T)> 0，则表示再保险公司承保后有效用收益；若L2(T)< 0，则表示再保险公司承保后有效用损失。如果L1(T)>0 且L2(T)> 0，则再保险合约可以成交；否则，至少一方有效用损失，再保险合约不能成交。

除非特别说明，各模型参数取值如表1 所示。

表1 数值例子中的各个模型参数值

3.1 保险公司占主导

由定理1 中的(19)，得下面的推论。

推论4 保险公司的最优自留比例a∗是α1的减函数，a∗是η的增函数，a∗是σ的减函数。

由于α1为保险公司绝对风险厌恶系数，α1越大，保险公司越厌恶风险，所以保险公司愿意分出更多的风险，自留比例越小。因为η为再保费，η越大，表明再保险成本越高，故保险公司自留更多风险。由于σ是保险公司的赔付大小，σ越大，保险公司面临的赔付风险越大，所以保险公司自留更少的风险。

图1 给出保险公司和再保险公司的效用损益与再保费η之间的关系。由图1 可知，保险公司和再保险公司都有效用收益，即在此再保费下，保险公司购买再保险和再保险公司承保都能提高其效用，再保险合约是可以成交的。保险公司的效用收益L1(T)随着再保费η的增加而减少，因为η越大，再保险成本越高，购买再保险需要花费更多财富，导致期望盈余效用减少。再保险公司的效用收益L2(T)是再保费η的先增后减函数，这与直观的再保费越高，再保险公司承保收取更多的保费，再保险公司具有更多的财富，从而期望盈余效用越大不一致。因为第一方面，再保费越高，再保险公司承保收取更多的保费导致再保险公司盈余增加；第二方面，再保费越高，再保险成本越高，保险公司购买更少的再保险导致再保险公司盈余减少。当再保费较小时，第一方面占主导，因此再保险公司的效用收益随着再保费的增加而增加；当再保费较大时，第二方面占主导，因此再保险公司的效用收益随着再保费的增加而减小。

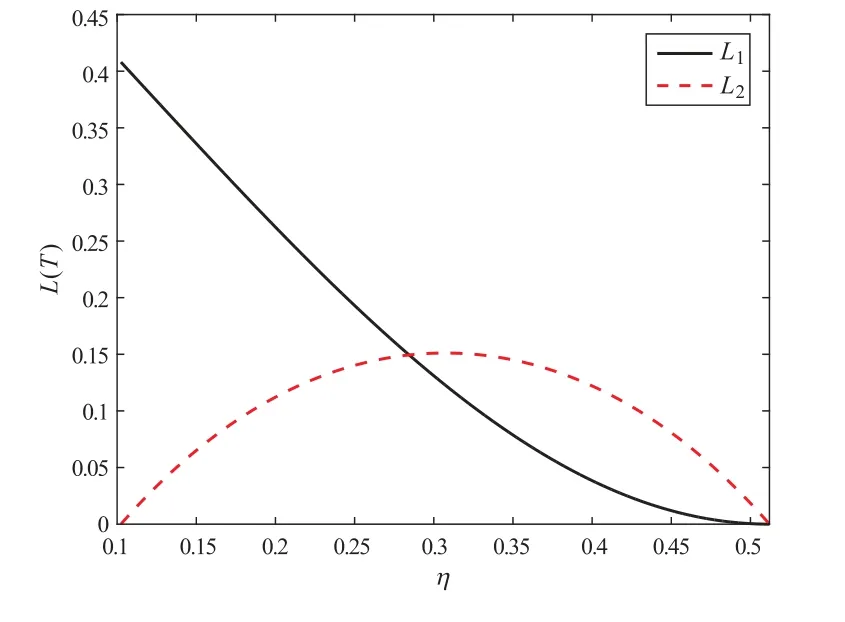
图1 效用损益与η 之间的关系

图2 给出保险公司和再保险公司的效用损益与保险公司的绝对风险厌恶系数α1之间的关系。由图2 可知，保险公司和再保险公司都有效用收益，保险公司和再保险公司的效用收益都随着α1的增加而增加。因为α1为保险公司的绝对风险厌恶系数，α1越大，保险公司越厌恶风险，承担风险需要更多的补偿，导致效用收益增加。从图2 还可以发现，α1对保险公司的效用收益L1(T)影响敏感，对再保险公司的效用收益L2(T)影响不敏感。因为α1为保险公司的绝对风险厌恶系数，直接影响保险公司的效用收益，而对再保险公司效用收益的影响是通过再保费传导过来。因此，α1对再保险公司的效用收益影响没有对保险公司的效用收益的影响敏感。

图2 效用损益与α1 之间的关系

3.2 保险公司和再保险公司共同主导

推论5 再保险公司最优再保费η∗是σ和α2的增函数，保险公司最优自留额ˆa∗是α2的增函数。

所以ˆa∗随着α2的增大而增大。

由于σ越大，再保险公司承保面临的赔付风险越大，所以再保险公司要求更多的再保费。由于α2为再保险公司绝对风险厌恶系数，α2越大，再保险公司越厌恶风险，所以再保险公司承保需要更多的再保费，同时导致保险公司的再保险成本越高，故保险公司自留更多的风险。

由推论2 可知

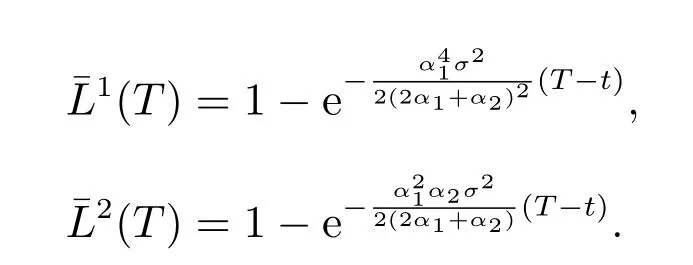
图3 给出保险公司和再保险公司的效用损益与保险公司的绝对风险厌恶系数α1之间的关系。由图3 可知，保险公司和再保险公司都有效用收益，再保险合约是可以成交的。保险公司和再保险公司的效用收益都随着α1的增加而增加，并且再保险公司的效用收益大于保险公司的效用收益。

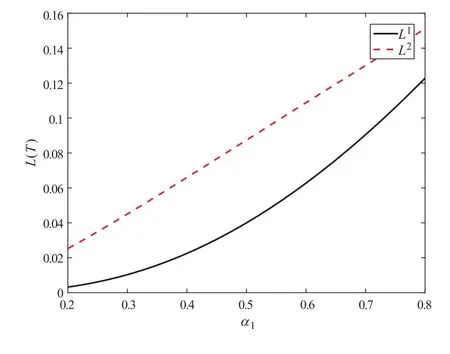
图3 效用损益与α1 之间的关系

图4 给出保险公司和再保险公司的效用损益与再保险公司的绝对风险厌恶系数α2之间的关系。由图4 可知，保险公司和再保险公司都有效用收益。同时，由图4 可知，保险公司的效用收益随着α2的增加而减小，而再保险公司的效用收益是α2的增函数。由推论5 可知，再保费和保险公司的最优自留额都是α2的增函数。因此，随着再保险公司绝对风险厌恶系数的增加，再保险公司承保收取更多的再保费，导致保险公司的期望盈余效用减小，再保险公司的期望盈余效用增加。

图4 效用损益与α2 之间的关系

3.3 再保险公司占主导

由定理4 中的(38)，易得下面的推论。

推论6 再保险公司的最优承保比例1−a∗是σ和α2的减函数，是η的增函数。

由于σ越大，再保险公司承保面临的赔付风险越大，因此再保险公司承保更少的再保险。由于α2为再保险公司绝对风险厌恶系数，α2越大，再保险公司越厌恶风险，所以再保险公司只愿意承担更少的风险，承保比例越小。因为η为再保险公司的再保费，η越大，表明承保能获得更多的收益，故再保险公司承保更多的风险。

图5 给出保险公司和再保险公司的效用损益与再保费η之间的关系。由图5 可知，保险公司和再保险公司都有效用收益。再保险公司的效用收益随着再保费η的增加而增加，因为η越大，承保能获得更多的收益，所以再保险公司的效用收益会增加。保险公司的效用收益是再保费η的先增后减函数。因为再保险公司决定承保比例，第一方面，再保费越高，再保险成本越高，购买再保险导致保险公司盈余减少；第二方面，再保费越高，再保险公司承保比例越高，保险公司面临的风险在减小，导致保险公司盈余会增加。当再保费较小时，第二方面占主导，因此保险公司的效用收益会增加；当再保费较大时，第一方面占主导，因此保险公司的效用收益会减小。

图5 效用损益与η 之间的关系

图6 给出保险公司和再保险公司的效用损益与σ之间的关系。由图6 可知，保险公司的效用收益随着σ的增加而增加，而再保险公司的效用收益是σ的减函数。因为再保险公司决定承保比例，σ越大，由(38)可知再保险公司承保更少的再保险，保险公司分出更少的保费，所以保险公司的效用收益会增加，再保险公司的效用收益会减少。

4 结论

本文在扩散风险模型下考虑了保险公司和再保险公司之间的再保险策略选择博弈问题。在保险公司和再保险公司都具有指数效用函数条件下，得到了三种博弈情形下保险公司和再保险公司之间的再保险策略的显示解，以及再保险合约能够成交时再保费满足的条件。通过数值计算得到效用损益与模型主要参数之间的关系，并给出相应的经济分析。

本文仅仅考虑在三种博弈情形下再保险合约能够成交的条件，并且再保险公司没有参与其它的保险活动，其收入来源完全由再保险保费构成。在后续的研究中，将考虑再保险公司本身具有保险业务，并将引入投资，即保险公司和再保险公司都投资于金融市场，并且金融市场与保险市场相关，探讨投资对再保险合约成交的影响。