基于关联矩阵和动态规划法的地区电网无功优化

郑爱霞，陈星莺，余 昆，葛思敏，罗志坤，刘潇潇



基于关联矩阵和动态规划法的地区电网无功优化

郑爱霞1，陈星莺2,3，余 昆2,3，葛思敏2，罗志坤4，刘潇潇4

(1.江苏省电力公司电力科学研究院，江苏 南京 210019；2.河海大学能源与电气学院，江苏 南京 211100；3.江苏省配用电与能效工程技术研究中心，江苏 南京 211100；4.国网湖南省电力公司电力科学研究院，湖南 长沙 410000)

针对目前时段划分中对动作次数的处理和模型简化方面存在的问题，设计设备状态的关联矩阵，并据此进行时间区间划分。在此基础上，对每个时段进行静态无功优化，保留每个时刻的最优解和部分次优解，并将这些解作为动态规划的状态变量。在各时段中用动态规划法以动作次数最小为目标寻找最优路径，从而得到整个调度周期的动态无功优化问题的解。某实际地区电网算例说明了时段划分和基于此的动态无功优化方法的有效性。

动态无功优化；地区电网；动态规划；设备状态关联矩阵

0 引言

地区电网无功优化是通过调节变压器分接开关和无功补偿装置状态来优化电网潮流分布[1]，控制调节的开关设备由于设备制造等原因具有严格的设备动作次数限制，在实际工作中为了适应负荷的动态变化，需要计及调节设备的动作次数约束，这将无功优化问题变成一个复杂的动态优化问题[2-3]。目前，对该问题的处理可以总结为三大类：(1) 简化动态规划法的求解空间[4-6]；(2) 通过分段简化成静态无功优化问题[7-11]；(3) 将费用作为目标函数进行简化，将控制变量的动作次数约束还原为经济成本来处理[12]。

上述研究中，动作次数有两种定义：(1) 控制变量在调度周期内的取值变化次数[13]；(2) 对应开关在调度周期内的投切次数[14]。采用定义一时可以通过一系列简化措施来保证动作次数约束，从而简化模型，比如使控制变量的调节时段数或者负荷曲线的分段数等于设备最大动作次数限制，认为在每个分段区间上控制设备任意变化都不会违反约束，将动态无功优化问题转化为几个时段的静态无功优化，从时间上进行解耦[15]。这种方法可能导致控制变量单次调节幅度过大。第二种定义与实际情况相符，能够保证控制策略的可操作，但不可避免地增加了问题的求解难度，因为实际工作中允许同一开关在每个时段动作两次及以上，这样不能简单地将分段数和动作次数关联。同时，如果将每个电容器和变压器分接头都当做一个独立变量，还会大大增加模型的规模。除此之外，文献[16]用控制设备开关动作的调节代价罚函数来代替动作次数约束，化解动作次数限制的硬性约束，但实际上动作代价包含动作率和设备寿命两层含义，动作频繁寿命会减少，动作率太低则造成设备浪费。

本文的动态无功优化问题分为两个步骤：首先设计设备状态和时间关联的矩阵来反映相邻时刻设备动作情况，并指导整个调度周期内各个时间区间的合并；其次在时间区间划分的基础上对每个时段进行静态无功优化，保留每个时刻的最优解和部分次优解，并将这些解作为动态规划的状态变量，在各时段中用动态规划法以动作次数最小为目标寻找最优路径。

1  电网动态无功优化数学模型

考虑到地区电网以220 kV变电站为中心成辐射状供电的特性，可以将优化问题分解为针对各独立子网的优化问题[17]。以下的讨论均针对一个辐射状网络，假设共有条母线，台可投切的电容器，个带有有载调压分接头的变压器。考虑到需要尽量减小网络损耗和设备动作次数[18]，这里多时段无功优化模型采用网络一天内的损耗、电容器与变压器有载分接开关动作次数来构造目标函数[19]，控制手段为变压器有载分接开关的调节和并联电容器组的投切。并联电容器组日动作次数限制为，变压器有载分接开关的日动作次数限制为。其具体模型如下所示。

2  基于关联矩阵分析的时间区间划分

时间区间分段法的主要思想是将地区电网动态特征相同或者相似的时段划分在同一个区间内，以避免设备不必要的动作。根据上面的分析，本文将设备状态-时间关联矩阵作为时间区间划分的依据。

2.1 设备状态-时间关联矩阵

在动态无功优化问题中，每个设备受动作次数限制，使其成为一个复杂的时空耦合问题[20]。单个设备的动作不仅受不同时刻情况的影响，还受同一时刻不同设备动作情况的影响。相邻时刻，负荷特性相近，达到最优状态时设备的状态也大致相同，因此相邻时刻设备的动作总次数在一定程度上能反映相邻时刻的相似程度。本文定义设备状态-时间关联矩阵如图1所示。

图1 设备状态-时间关联矩阵

图2 动作次数-时间关联矩阵

单一时间断面，每个设备都可能有不同的动作次数，如果简单地以所有设备总动作次数来表征相邻时刻设备的变化状态不合理，因为在地区电网无功优化中控制变量考虑两个，分别是电容器和有载变压器，两者的动作不等价，主要表现在一般情况下电容器分三组，每个电容器日动作不超过10次，有载分接开关有7档，日调节次数不超过30次。因此这里需要对设备动作次数进行“等效”，即标准化。本文设立相邻时刻设备状态变化指标，用于在单个时刻最优状态基础上判断相邻两个时刻是否应该合并。其表示方法为

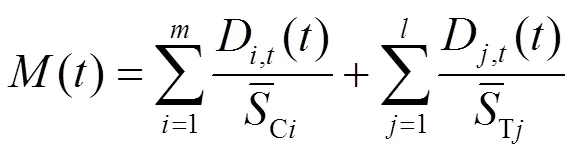
通过对矩阵,,的分析，在动作次数满足约束条件下，对一天24个时段进行划分。采用本文方法无需事先规定区间个数，而是在时段合并过程中不断比较一天的网损值，如果随着合并的进行，减少的网损费用小于设备的动作代价时，就取消相应的合并，且以此刻的分段数作为最终分段结果，继而进行段内的静态无功优化。据此，设立分段终止判据为

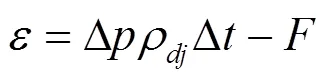
2.2 时间区间划分步骤

在时间区间的划分过程中，首先要满足每个设备的动作次数限制，然后根据动作次数对近似时刻进行合并，在动作次数满足要求之前并不进行合并结束的判断，只有合并进入动作次数约束区间内后，才根据合并终止判据进行判断是否结束合并，合并时刻确定的顺序则是根据每个时刻总的动作次数来决定。具体步骤如图3。

图3 时间区间划分流程

(1) 根据母线预测负荷对每个时刻进行以网损最低为目标的静态无功优化，得到每个时刻最优状态下设备的状态，形成设备状态-时间关联矩阵、动作次数-时间关联矩阵以及每个时刻的设备状态变化矩阵。

(2) 对设备状态变化矩阵内元素进行排序，对取值最小的时刻依次进行合并，以两个时刻的平均负荷进行静态无功优化，求出合并时刻最优状态下的设备状态，并更新矩阵、、；

(3) 对矩阵每行求和即为当前设备日动作次数，判断与设备最大动作次数、的关系，如果不满足则跳至步骤(2)继续进行合并；如果满足则跳至步骤(4)进行是否终止合并的判断。

(4) 分别统计合并前后一天的网络损耗，并根据动作次数的变化计算设备动作代价，得到终止判断判据，如果，则继续进行合并，并跳至步骤(2)；如果，则终止合并。

(5) 整理时段划分区间，输出结果。

3  基于动态规划法的设备动作序列优化

考虑到一天的设备动作次数约束，在时间区间划分基础上，选用可投切电容器和有载调压变压器作为控制变量，动态规划过程中的状态量用可投切电容器的组数和有载调压变压器的分接头表示。状态变量可以表示为

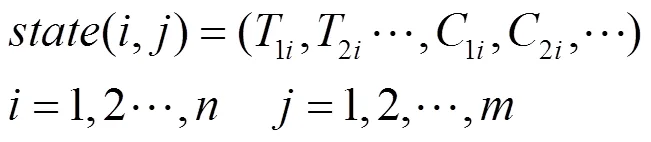
(5)

(7)

按照时间区间划分后，每个阶段都有对应的子问题，求解最优问题的关键是求解每个阶段的最优解，动态规划法求解无功优化问题的步骤如图4。

图4 动态规划法设备动作序列优化

(3) 依次求解能够达到第2阶段其他状态的累计目标函数值，并记录各自目标函数取最小值时的状态变量，完成第2阶段的所有子问题求解；

(5) 根据各阶段记录的最优子策略回溯，得到整个调度周期内的最优控制策略序列。

4  算例

本文采用一典型的实际地区电网作为仿真网络，见图5。其基本情况如下：共六台变压器，其参数见表1变压器参数，除T1档位调节范围为外，其余均为；6台可投切电容器组，其配置情况见表2；5条输电线路，其参数见表3；6个负荷节点，其母线负荷预测曲线见图6和图7。共涉及三个电压等级，其基准值分别为220 kV、110 kV和10 kV，系统基准功率为，母线电压合格范围取为1.00~1.07。

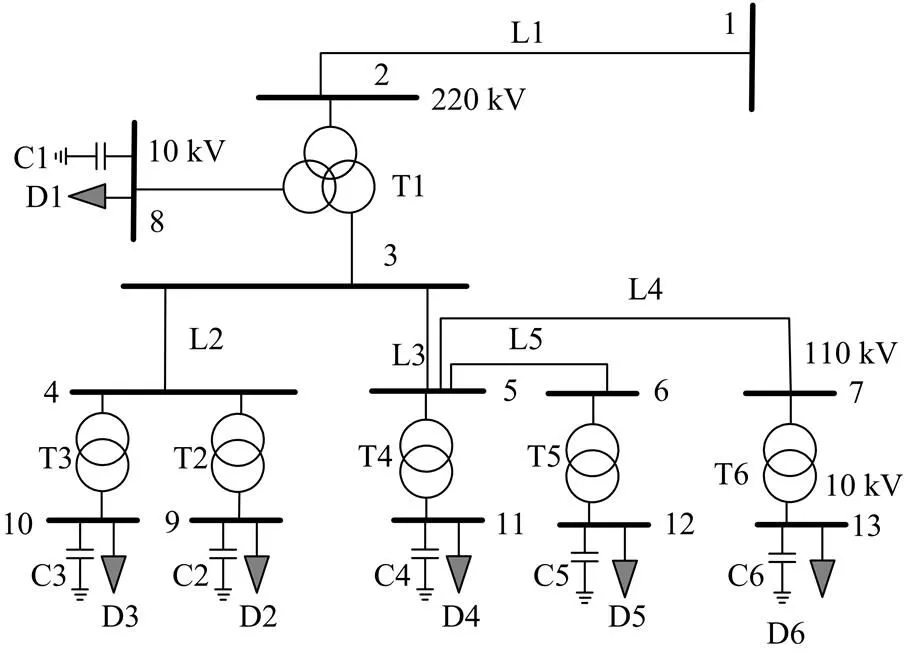
图5 仿真网络接线图

(1) 根据实际运行状况，并联电容器和有载调压变压器分接开关的每天最大允许动作次数约为8次和30次，本文将设备动作次数约束适当放大，寻找在满足设备动作次数约束的情况下，合并后段数和设备动作次数之间关系，如图8；合并后段数与网损之间的关系如图9。结果表明随着合并的进行设备动作次数逐渐减少，但合并后日网损增大，可见设备动作次数的减少的代价是牺牲网损，本文根据网损和设备动作综合代价作为判据确定分段数具有实际意义。

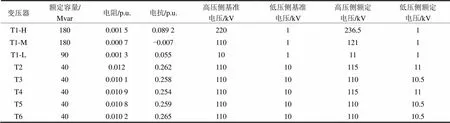
表1 变压器参数

表2 可投切电容器组配置情况

表3 输电线路数据

图6 母线有功负荷预测曲线

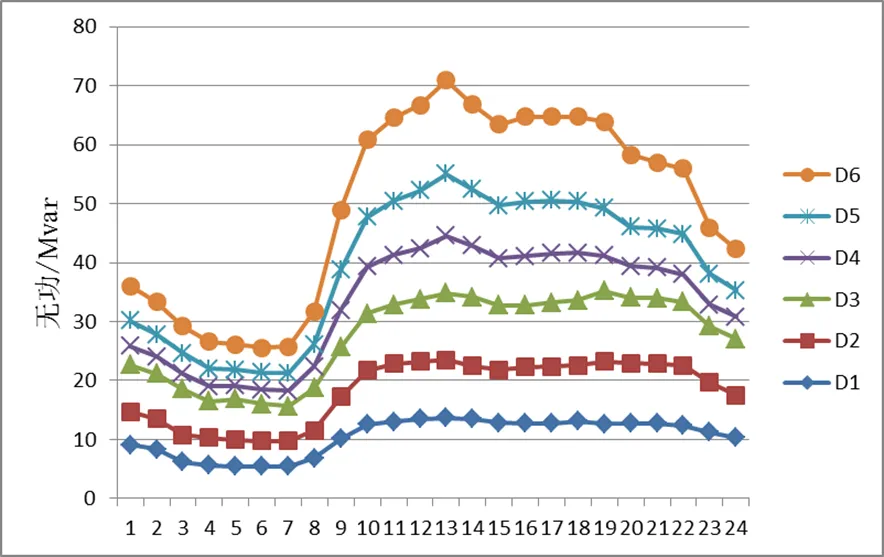
图7 母线无功负荷预测曲线

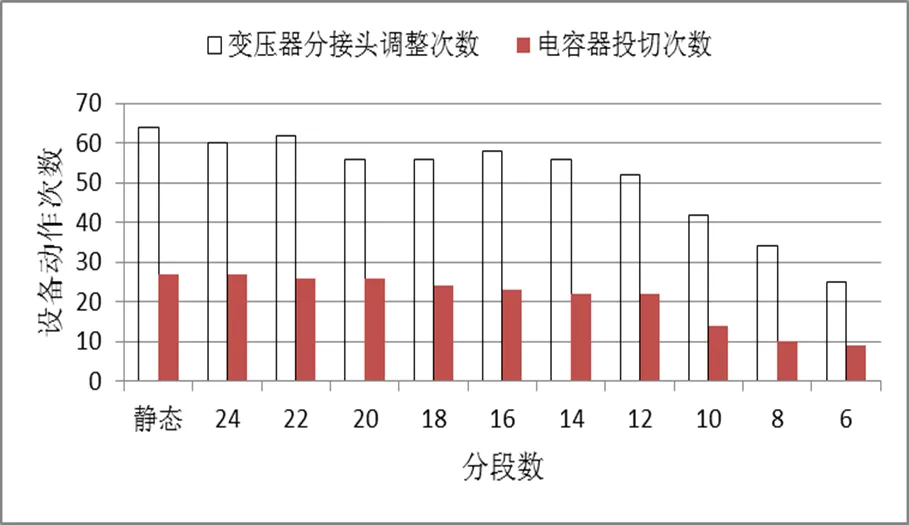
图8 时段合并过程设备动作次数关系

为了反映变压器分接开关的动作情况，图10给出了单点静态优化和分段数为8时的T1变压器分接开关调整情况，同静态优化的结果相比，分段优化避免了变压器分接头大幅跳跃性动作。同时可以看出，变压器分接头一次可能调节2档(如时刻1-2)，按照实际情况此刻的动作次数应该记为2次。按照最大设备动作次数为分段数的方法不能考虑到这种情况，如果有一个分段区间变压器分接开关调整2档及以上，并且其他区间都动作，那么这样的分段就不能满足设备动作次数的限制；另外一种情况是设备未必会在每个分段区间都动作，通过设备最大动作次数分段方法实际上减少了可能的分段数，缩小降损空间。本文在充分了解每个时段设备动作情况下，进行分段避免这些问题，最终根据判据在电容器最大动作次数约束为6次的情况下，将一天24 h分为7段也表明了这一点。

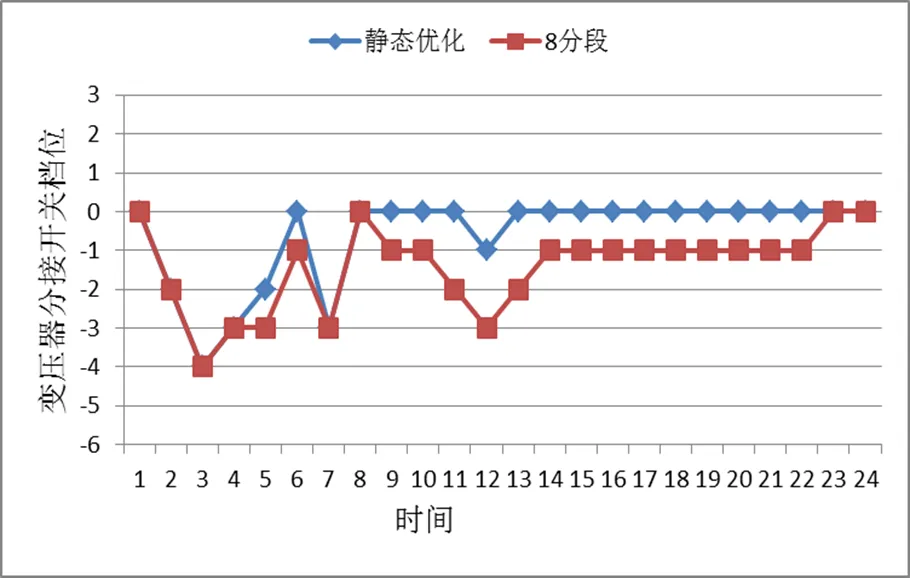
图10 T1变压器分接头动作曲线

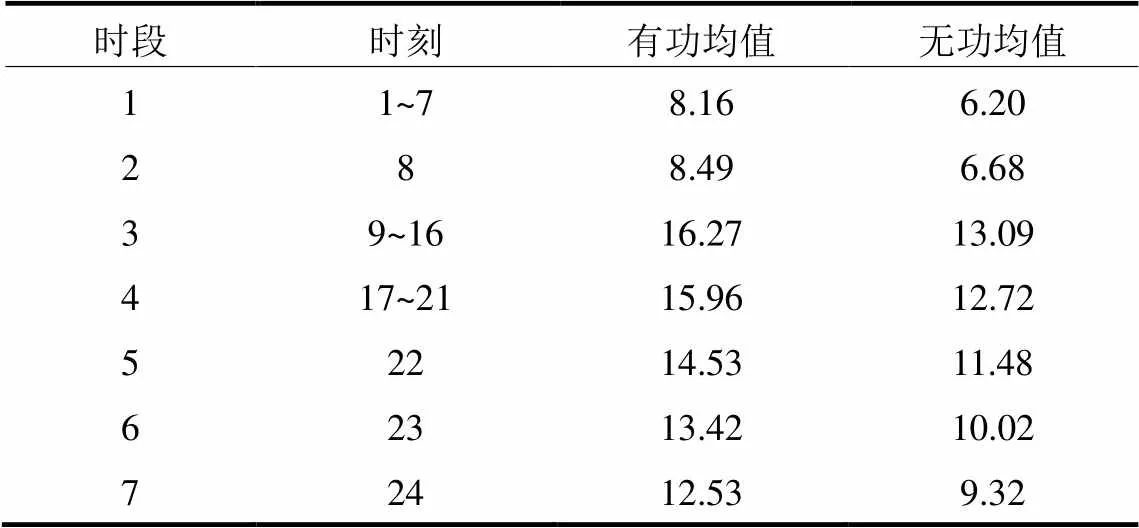
表4 时间区间划分结果

(2) 在动态分段过程中，最后一次分段时已经求出了每分段的最优设备状态，但这一状态是基于前分段设备状态已经确定的情况下得出，由此得到的整个调度周期的最优设备动作时间序列并不一定最优，整个调度周期的动作次数最优解很可能在包含一系列次优解的序列中。根据本文动态规划法优化设备动作次数的思路求解结果和分段过程中得出的最优状态比较见表5，对比分析动态规划算法优化设备动作次数前后可知，利用动态规划算法优化控制设备的动作次数之后，损耗增加了0.33 MW，但是一天内主变动作次数减少了9次，电容器动作次数减少了3次，在能耗增幅较小的情况下减少了有载调压分接开关和电容器的总投切次数，最重要的是结合时间区间的划分情况，优化了每个设备的动作次数和动作时间，延长了设备的使用寿命。

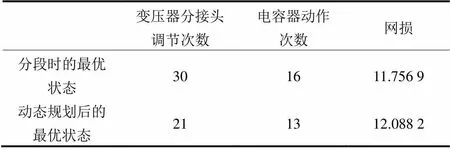
表5 动态规划优化后最优状态情况比较

5  结论

本文主要研究了地区电网动态无功优化的问题，分为两个主要步骤：首先对于目前时段划分中所存在的不足进行总结，并且提出了基于关联矩阵反映相邻时刻设备动作情况，指导整个调度周期内各个时间区间的合并；其次在时间区间划分的基础上对每个时段进行静态无功优化，保留每个时刻的最优解和部分次优解，并将这些解作为动态规划的状态变量，在各时段中用动态规划法以动作次数最小为目标寻找最优路径。最后通过一个实际地区电网算例说明了本文时段划分和基于此的动态无功优化方法的有效性。

[1] 张勇军, 任震, 李邦峰. 电力系统无功优化调度研究综述[J]. 电网技术, 2005, 29(2): 50-56.

ZHANG Yongjun, REN Zhen, LI Bangfeng. Survey on electric system reactive power optimal scheduling[J]. Power System Technology, 2005, 29(2): 50-56.

[2] 康忠健, 訾淑伟. 基于差分进化算法的油田区域配电网无功优化技术的研究[J]. 电工技术学报, 2013, 28(6): 226-231.

KANG Zhongjian, ZI Shuwei.Research on the reactive power optimization of oil-field regional distribution network based on differential evolution[J].Transactions of China Electrotechnical Society, 2013, 28(6): 226-231.

[3] 陈丽, 张晋国, 苏海锋. 考虑并网光伏电源出力时序特性的配电网无功规划[J]. 电工技术学报, 2014, 29(12): 120-127.

CHEN Li, ZHANG Jinguo, SU Haifeng.Reactive power planning for distribution system with grid-connected photovoltaic system considering time-sequence characteristics[J].Transactions of China Electrotechnical Society, 2014, 29(12): 120-127.

[4] HSU Y, KUO H C. Dispatch of capacitors on distribution system using dynamic programming[J]. Generation, Transmission and Distribution, IEE Proceedings C, 1993, 140(6): 433-438.

[5] LU F C, HSU Y Y. Fuzzy dynamic programming approach to reactive power/voltage control in a distribution substation[J]. IEEE Transactions on Power Systems, 1997, 12(2): 681-688.

[6] LIU Mingbo, TSO S K, CHENG Ying. An extended nonlinear primal-dual interior-point algorithm for reactive-power optimization of large-scale power systems with discrete control variables[J]. IEEE Power Engineering Review, 2002, 22(4): 56-56.

[7] DENG Y, REN X, ZHAO C, et al. A heuristic and algorithmic combined approach for reactive power optimization with time-varying load demand in distribution systems[J]. IEEE Transactions on Power Systems, 2002, 17(4): 1068-1072.

[8] 任晓娟, 邓佑满, 赵长城, 等. 高中压配电网动态无功优化算法的研究[J]. 中国电机工程学报, 2003, 23(1): 31-36.

REN Xiaojuan, DENG Youman, ZHAO Changcheng, et al. Study on the dynamic distribution network reactive power optimization algorithm[J].Proceedings of the CSEE, 2003, 23(1): 31-36.

[9] TERRA L D B, SHORT M J. Security-constrained reactive power dispatch[J]. IEEE Transactions on Power Systems, 1991, 11(2): 109-117.

[10] ZHAO B, GUO C X, CAO Y J. A multi agent-based particle swarm optimization approach for optimal reactive power dispatch[J]. IEEE Transactions on Power Systems, 2005, 20(2): 1070-1078.

[11] FERDOUS M J, ARAFAT Y, AZAM M A. Flicker level mitigation of weak grid connected wind turbine with DFIG by injecting optimum reactive power using STATCOM[C] // Informatics, Electronics & Vision (ICIEV), 2013: 1-5.

[12] KIMURA N, KASHIWAGI S, MORIZANE T, et al. Optimum control of reactive and real power in converter excited induction generator system for wind power generation[C] // Control and Modeling for Power Electronics (COMPEL), 2014: 1-7.

[13] 张勇军, 苏杰和, 羿应棋. 基于区间算术的含分布式电源电网无功优化方法[J]. 电力系统保护与控制, 2014, 42(15): 21-26.

ZHANG Yongjun, SU Jiehe, YI Yingqi. Reactive power optimization based on interval arithmetic with distributed power grid[J].Power System Protection and Control, 2014, 42(15): 21-26.

[14] 赵冬梅, 邱辰, 张旭.地区电网可视化实用无功优化与规划系统的设计[J]. 电力系统保护与控制, 2013, 41(3): 123-127.

ZHAO Dongmei, QIU Chen, ZHANG Xu.Design of visual and practical reactive power optimization and planning system in area network[J].Power System Protection and Control, 2013, 41(3): 123-127.

[15] 吕忠, 周强, 蔡雨昌. 含分布式电源的DEIWO算法配电网无功优化[J]. 电力系统保护与控制, 2015, 43(4): 69-73.

LÜ Zhong, ZHOU Qiang, CAI Yuchang.Reactive power optimization in distribution network with distributed generation on DEIWO algorithm[J].Power System Protection and Control, 2015, 43(4): 69-73.

[16] 张勇军, 任震. 电力系统动态无功优化调度的调节代价[J]. 电力系统自动化, 2005, 29(2): 34-38.

ZHANG Yongjun, REN Zhen.Readjusting cost of dynamic optimal reactive power dispatch of power systems[J].Automation of Electric Power Systems, 2005, 29(2): 34-38.

[17] HU Z, WANG X, CHEN H, et al. Volt/Var control in distribution systems using a time-interval based approach[J]. IET Proceedings — Generation, Transmission, and Distribution, 2003, 150(5): 548-554.

[18] LIU M B, CANIZARES C A, HUANG W. Reactive power and voltage control in distribution systems with limited switching operations[J]. IEEE Transactions on Power Systems, 2009, 24(2): 889-899.

[19] 周鑫, 诸弘安, 马爱军. 基于多种群蚁群算法的多目标动态无功优化[J]. 电网技术, 2012, 36(7): 231-236.

ZHOU Xin, ZHU Hongan, MA Aijun.Multi-objective dynamic reactive power optimization based on multi- population ant colony algorithm[J].Power System Technology, 2012, 36(7): 231-236.

[20] 刁浩然, 杨明, 陈芳, 等. 基于强化学习理论的地区电网无功电压优化控制方法[J]. 电工技术学报, 2015, 30(12): 408-414.

DIAO Haoran, YANG Ming, CHEN Fang, et al.Reactive power and voltage optimization control approach of the regional power grid based on reinforcement learning theory[J].Transactions of China Electrotechnical Society, 2015, 30(12): 408-414.

(编辑 姜新丽)

Reactive power optimization of district power grid based on associated matrix and dynamic programming method

ZHENG Aixia1, CHEN Xingying2, 3, YU Kun2, 3, GE Simin2, LUO Zhikun4, LIU Xiaoxiao4

(1. Jiangsu Electric Power Research Institute, Nanjing 210019, China; 2. College of Energy & Electrical Engineering,Hohai University, Nanjing 211100, China; 3. Jiangsu Engineering Research Center for Distribution & Utilization andEnergy Efficiency, Nanjing 211100, China; 4. Hunan Electric Power Research Institute, Changsha 410000, China)

In order to solve the problem of action number handing and model simplification in present time division, the associated matrix on equipment state is designed and the time is divided into several intervals based on this matrix. And then static reactive power of each time interval is optimized, the optimum solution and second best solution of each time interval are reserved. Then these solutions are used as state variables of dynamic programming to search the optimum path which has smallest time of action using dynamic programming in each time interval. At last, the solution of dynamic reactive power problem during whole scheduling period can be gotten. An example of region power system shows the effectiveness of time division and dynamic reactive power optimal method based on it.

dynamic reactive power optimization; district power grid; dynamic programming; associated matrix on equipment state

10.7667/PSPC150849

国家电网公司科技项目(智能变电站能效评测与能效提升关键技术研究与试点工程建设)；国家发改委物联网专项(基于物联网的智能用电综合管理与能效提升技术研发及产业化)

2015-05-19；

2015-12-08

郑爱霞(1968-)，女，硕士，高级工程师，从事电力设备运维、无功电压、电网节能降损、电能计量等工作；E-mail: alice6808@sohu.com 陈星莺(1964-)，女，博士，教授，博士生导师，主要研究方向为配用电规划与评估、智能配电网运行分析、配电网智能调度与控制、高效用电与节能、能源管理与能源经济；E-mail: xychen@hhu.edu.cn 余 昆(1978-)，男，博士，副教授，硕士生导师，研究方向为配用电规划与评估、智能配电网运行分析、配电网智能调度与控制。E-mail: kun.yu@vip.sina.com