基于纵横交叉算法的热电联产经济调度

孟安波，梅 鹏，卢海明



基于纵横交叉算法的热电联产经济调度

孟安波，梅 鹏，卢海明

(广东工业大学自动化学院, 广东 广州 510006)

为解决热电联产经济调度优化问题，提出了一种基于纵横交叉算法(Crisscross optimization algorithm，CSO)的新求解方法。CSO采用一种双交叉搜索机制，其中横向交叉引入扩展因子增强全局搜索能力，纵向交叉引入维交叉概念，从而避免维局部最优问题。CSO的全局并行搜索，避免了陷入局部最优，有效提高了收敛速度。以一个包含纯发电机组、热电联产机组、纯发热机组的48机组系统为例，建立了热电联产经济调度问题的模型。仿真结果表明，CSO解决热电联产经济调度问题具有可行性和有效性，为实际调度系统提供了一个较好的方法。

热电联产；经济调度；纵横交叉算法；维局部最优；并行搜索

0 引言

目前，大部分发电厂的能源利用率低于60%，但是热电联产机组(CHP)的燃料利用效率高达90%，并且能减少13%~18%的污染物(CO2, SO2, SOx和NOx 等)[1-2]。随着环境问题的日趋严重，减少化石燃料的使用，提高燃料利用率已成为共识。优化热、电两类负荷指令的分配方式，能大大降低燃煤电厂的单位能耗，对节能减排有重要意义。

热电联产经济发电调度优化问题(CHPED)是一个非线性、多约束条件、非凸性的优化问题，关键是要使总成本最小，并且在考虑到机组的约束条件下，满足系统的电力和热量需求[3-4]，传统的纯数学优化算法难以解决这一问题。许多研究者提出了不同的优化方法。为测试这些方法的优劣，广泛使用了Guo[5]于1996年提出的模型。Guo使用了拉格朗日松弛算法(LR)[5]，此后还有蚁群优化算法(ACO)[6]、基于乘法器更新的改进遗传算法(GA-MU)[7]、带精英策略的快速非支配排序遗传算法(NSGA-II)[8]、和声算法(HS)[9]、蜂群算法(BCO)[10]、差分进化算法(DE)[11]、网格自适应直接搜索算法(MADS)[12]等；另外还有一部分以粒子群算法(PSO)为基础的改进算法，有混合粒子群算法(HPSO)[13]、时变加速常数粒子群算法(TVAC-PSO)[14]、时变加速常数迭代粒子群算法(IPSO-TVAC)[15]等。

纵横交叉算法(CSO)[16]是作者提出的一种全新的基于种群的随机搜索算法。有两种不同的交叉方式，能较好地解决一般智能算法存在的局部最优问题。本文根据热电联产机组的能耗特点，引入罚函数构建目标函数，应用纵横交叉算法(CSO)进行求解，充分发挥了纵横交叉算法(CSO)的全局搜索能力与局部搜索能力，既提高了收敛速度，又提高了算法精度。应用一个含48机组的测试系统进行仿真计算，并对比了其他算法，验证了纵横交叉算法(CSO)求解CPHED问题的有效性和适用性。

1  热电联产经济调度优化问题模型

1.1 热电负荷目标函数

热电联产经济调度优化问题的实质是合理调度分配各个机组的热电负荷出力，在满足负荷需求和各项约束条件后，使得系统总的运行成本最小。本系统包含普通火电机组、热电联产机组以及发热机组。

考虑发电机组的阀点效应，使得热电联产经济调度问题成为一个非线性、不可微问题。这样提高了问题求解的精确度[17-19]。这个问题数学上可以表示如下。

(2)

(3)

式中：T为总成本；ti(P)第台纯发电机组成本；ci(O, H)第台热电联产机组成本；hi(T)为第台纯发热机组成本；p,c,h分别是纯发电机组，热电联产机组，纯发热机组的台数；P为第台纯发电机组的出力；O,H为第台热电联产机组的发电量和发热量；T为第台纯发热机组的发热量；Pmin为第台纯发电机组的下限；a,b,d,e,f为第台纯发电机组的成本系数；α,β,γ,δ,ε,ξ为第台热电联产机组的成本系数；φ, η, λ为第台纯发热机组的成本系数。

1.2 约束条件

1.2.1 系统负荷平衡约束条件

系统中的热电产量应能满足负荷需求，如下所示。

(6)

式中：D为电负荷需求；D为系统的热负荷需求。

1.2.2 机组出力约束条件

1) 发电机组的出力除了有上下限，还有禁止运行区域，约束条件为

2) 图1表示了热电联产机组的热电耦合关系，是由定点ABCVDEF连线所围成的封闭区域。沿着区域的边界线段BC，机组发热量递增，出力递减，而沿着线段CD机组发热量则递减[19]。

(9)

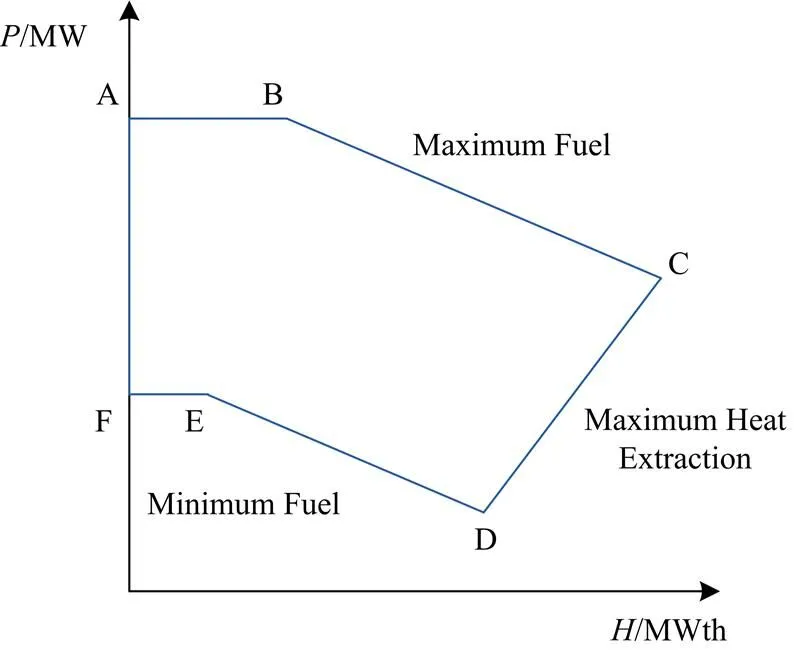
图1 热电联产机组运行区域

3) 纯发热机组的运行约束条件如式(10)。

2  纵横交叉优化算法

遗传算法(GA)的交叉操作每一代都会依概率进行横向交叉操作，但高维复杂问题，往往具有多个局部最优点，导致单一的交叉方式容易陷入局部最优[20]。在优化迭代的过程中，对多维寻优问题，还存在维局部最优的问题。当整个种群还未搜索到全局最优的时候，但有些维已经达到最优，进而影响适应度评价，改变了整个种群的迭代方向，使得种群陷入局部最优。为解决这个问题，纵横交叉算法在迭代过程中每一代都会进行横向交叉和纵向交叉两种交叉方式，从而使得种群中某些陷入维局部最优的维有机会跳出迭代。纵横交叉算法每次交叉后得出的解称为中庸解 (hc,vc)，通过引入竞争算子，使得这两种交叉方式有机的结合起来：每次交叉操作之后都会进入竞争算子，与父代进行竞争，只有比父代更优秀的粒子会被保留下来进入下次迭代，得出的解称为占优解 (hc,vc)。

2.1 横向交叉操作

横向交叉类似于GA的交叉操作，是在种群中两个不同个体粒子相同维之间进行的一种算数交叉。假设父代个体粒子()和()的第维进行横向交叉，则它们产生子代的公式如下

(12)

式中：1,2是[0, 1]之间的随机数；1,2是[-1, 1]之间的随机数；(,),(,)分别是父代种群中个体粒子()和()的第维；hc(,)和hc(,)分别是(,)和(,)通过横向交叉产生的第维子代。

不同个体粒子的相同维度的上下限范围是相同的，从社会学的角度来看，式(11)中的1×(,)是粒子()的记忆项，是粒子本身的当前最优值。 (1-1)×(,)是粒子()和()的群体认知项，表示了不同粒子间的相互影响。这两项通过惯性权重因子1较好的结合在一起。1是学习因子，第三项1×((,)-(,))可以增大搜索区间，在边缘寻优。横向交叉操作完成后，得到的中庸解hc(,),hc(,)必须分别与父代粒子(),()的适应度比较，只有适应度更好的中庸解才可以保留下来，成为占优解hc，参与下一次迭代。

2.2 纵向交叉操作

纵向交叉是种群中一个粒子的两个不同的维之间进行的一种算数交叉。由于不同维元素的取值范围不同，因而交叉前须将两维进行归一化处理，并且为了使已陷入维局部最优而停滞的那一维跳出局部最优而又不破坏另外一维的信息，每次纵向交叉操作只产生一个子代粒子，只对其中一维进行更新。假定粒子()的第1维和第2维是参与纵向交叉，根据公式(13)产生中庸解vc(,1)。

式(13)中的第一项是粒子()的第1维的记忆项，第二项是粒子()的第1维和第2维相互影响，通过惯性权重因子结合在一起。这样得到的中庸解vc(,1)不但包含父代粒子()的第1维的信息，还依一定概率含有()的第2维信息，并不会破坏()的第2维信息。中庸解vc(,1)与父代粒子()比较适应度，较好的保留下来作为占优解vc，进行下一次迭代。

2.3 全局搜索性

在实际工程应用中，绝大多数群智能优化算法的早熟问题往往是因为种群的部分维陷入了停滞不前，称之为维局部最优，纵向交叉方式不仅能使陷入局部最优的维有机会摆脱出来，进而使整个种群摆脱局部最优，同时它的变异方式能较好的维持种群的多样性。

横向交叉让种群内的粒子进行两两配对，将多维问题空间划分成了种群数目一半的子空间，以较大概率在以父代个体粒子()和()为对角顶点的超立方体内产生后代hc()和hc()。同时，为减少搜索盲点，利用纵向交叉以较小概率在超立方体外缘进行搜索，这种跨界搜索机制区别于遗传算法的交叉操作，有效地增强了算法的全局搜索能力。交叉后进入竞争机制，与其父代粒子进行比较，适应度更好的粒子得以保存。

两种交叉方式的有机结合不仅加速了种群的收敛速度，同时大大提高了收敛精度。一旦种群中某个个体粒子陷入停滞不前的维在纵向交叉作用下摆脱局部最优，会通过横向交叉的方式迅速传播至整个种群，而更新后的维也会使其余陷入局部最优的其他维有更多的机会通过纵向交叉跳出局部最优。两种交叉方式的结果会呈链式反应在整个种群中蔓延，相比其他群智能优化算法，这种纵横交叉机制使得CSO在全局收敛能力和收敛速度方面具有明显的优势。

3  CSO算法在热电联产经济调度问题中的应用

应用CSO算法解决热电联产经济调度优化问题的步骤如下。

1) 初始化策略

群搜索算法的初始种群会对算法迭代方向有一定的影响。种群中的每个粒子表示一个解，第个粒子可表示为

()是一个一维向量，每一维表示不同机组的热电负荷出力。跟据不同机组的出力和发热的最大最小值，设定每一维的上下限。随机产生一个符合各维大小限制的初始种群。

2) 计算适应度

调整好的粒子，计算适应度，依下式

式中：penish、penish为惩罚系数；前三项为总成本，第四、五项为惩罚成本。

计算种群每个粒子的适应度，适应度最好的粒子，记作：gbest。

3) 横向交叉

4) 纵向交叉

同一个粒子的不同维的上下限不同，所以在纵向交叉前要进行归一化。种群中粒子依单个粒子中所有维随机的两两配对。设粒子hX(i)的第1维和第2维进行交叉，为减少纵向交叉对某些已是最优维的影响，依式(13)只产生一个中庸解。计算中庸解的适应度，与父代hX(i)的适应度进行比较，保存适应度较好的作为占优解。将所有粒子进行反归一化操作，更新种群。

5) 保存全局最优

计算新种群每个粒子的适应度，保留适应度最好的粒子，记作：gbest。然后判断是否达到最大迭代次数，若没有则进行步骤2)，继续迭代；若达到最大迭代次数，则输出gbest，得到最终优化结果。

计算流程如图2所示。

图2 纵横交叉算法流程图

4  仿真实验分析

为验证CSO算法的有效性，本文算例采用48机组的热电联产系统来进行分析研究。这个模型由Mohammadi-Ivatloo[14]依据Guo[5]提出的4机组系统改进而来。算例使用Matlab2010a软件进行仿真。仿真在配置为Intel core i3、2.4 GHz CPU、4 GB RAM的计算机上进行。设定算法参数如下：种群粒子数量为30；最大迭代次数为2 000；横向交叉和纵向交叉的概率分别为1、0.8。实例机组出力单位为MW；发热量单位为MWth；成本单位为$。

测试系统包括26台纯发电机组，12台热电联产机组，10台纯发热机组，分别简称为机组1，2，3……48。其中机组1-13与机组14-26是相同的机组，机组27-32与机组33-38是相同的机组，机组39-43与机组44-48是相同的机组，机组1-13、27-32、39-43的参数以及约束条件如表1所示。热和电的负荷需求分别为2 500 MWth和4 700 MW。

表1 机组系统参数

热电联产机组的运行区域一般由多边形构成的封闭区域组成，图3为热电联产机组28，30，34，36的运行区域，热电联产机组27，29，31，33，35，37的运行区域与图3类似；图4为热电联产机组32，38的运行区域。

图3 热电联产机组28，30，34，36运行区域

图4 热电联产机组32，38运行区域

表2为优化后得到的各个机组出力及发热量，图5为目标函数适应度的迭代过程，同时引用了其他文献中相同系统数据。

表2 不同算法48机组系统仿真结果

图5 48机组系统成本迭代曲线

表3给出了不同算法的成本和运行时间。实验结果表明，CSO算法优化后的成本为114 544.708 4 $，比改进的粒子群算法的成本小，能提供有价值的运行策略。在与其他算法比较时，纵横交叉算法的寻优性能好、鲁棒性强、收敛速度快，可以较好的解决电力系统经济优化调度的问题。

表3 不同算法成本比较

图6给出了在[0,1]区间，间隔为0.05的不同纵向交叉概率下，50次实验，平均优化结果。在设定为0时，即未进行纵向交叉，实验的结果较差，成本较高，因为部分粒子的维度陷入了局部最优。可以看出在[0.2，0.8]区间内，成本较低，得出的解质量更高。因此纵向交叉概率设定为0.8，是依据经验而得出的参数值。这也是CSO唯一需要调整的参数，根据不同问题，建议选取[0.2，0.8]为宜。

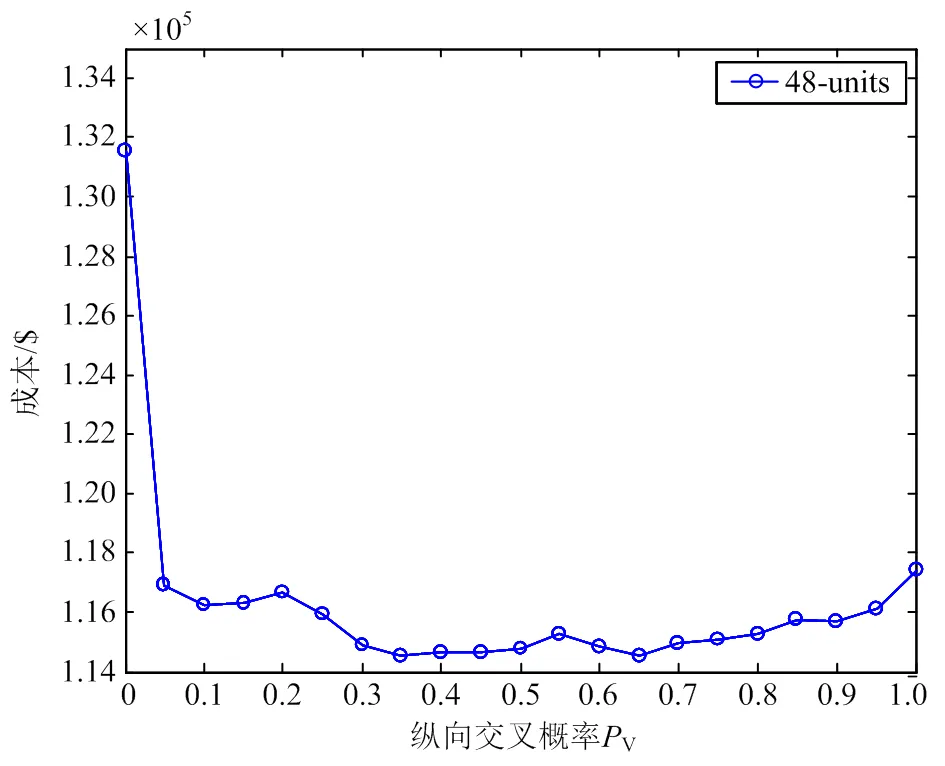
图6 不同纵向交叉概率条件下48机组系统平均成本

如图7所示，在纵向交叉概率设定为0.8条件下，50次实验得出的成本散点图。可以发现CSO优化的最差结果为114 622.034 1 $，小于其他四种算法优化的最优值，有一定的优势。CSO作为单一的优化算法，得出实验结果比混合PSO，TLBO有更好的表现，单一的参数调节机制，较为简单的算法结构，为解决优化类问题提供了一个较好的参考。

图7 50次实验下48机组成本分布散点图

5  结语

热电联产机组的合理利用能明显的提高能源利用率，本文引入含惩罚系数的调度评价函数，将热、电调度多目标问题转化为单目标问题，应用纵横交叉算法对两个系统进行仿真。分析实验结果可以得到以下结论：

1) 纵横交叉算法适用于非线性、多约束条件、非凸性的热电联产经济发电调度优化问题的求解。

2) 通过纵向的交叉机制，纵横交叉算法与改进粒子群算法比较，在解决存在多个局部最优点问题时纵横交叉算法更具优势。

3) 本文的经济调度模型中仅包含传统的热电机组，在此基础上，今后的研究内容还要考虑含风电[22]、太阳能[23]等分布式能源并网发电系统的经济调度，还要考虑环境经济调度[24]、动态系统的经济调度[18]、安全经济调度[25]等，使这个问题的模型更加全面，与实际情况更加接近。

[1] KARKI S, KULKARNI M, MANN M D, et al. Efficiency improvements through combined heat and power for on-site distributed generation technologies[J]. Cogeneration and Distributed Generation Journal, 2007, 22(3): 19-34.

[2] 崔红芬, 汪春, 叶季蕾, 等. 多接入点分布式光伏发电系统与配电网交互影响研究[J]. 电力系统保护与控制, 2015, 43(10): 91-97.

CUI Hongfen, WANG Chun, YE Jilei, et al. Research of interaction of distributed PV system with multiple access points and distribution network[J]. Power System Protection and Control, 2015, 43(10): 91-97.

[3] 陈洁, 杨秀, 朱兰, 等. 微网多目标经济调度优化[J]. 中国电机工程学报, 2013, 33(19): 57-66.

CHEN Jie, YANG Xiu, ZHU Lan, et al. Microgrid multi-objective economic dispatch optimization[J]. Proceedings of the CSEE, 2013, 33(19): 57-66.

[4] NIKNAM T, AZIZIPANAH-ABARGHOOEE R, ROOSTA A, et al. A new multi-objective reserve constrained combined heat and power dynamic economic emission dispatch[J]. Energy, 2012, 42(1): 530-545.

[5] GUO T, HENWOOD M I, VAN OOIJEN M. An algorithm for combined heat and power economic dispatch[J]. IEEE Transactions on Power Systems, 1996, 11(4): 1778-1784.

[6] SONG Y H, CHOU C S, STONHAM T J. Combined heat and power economic dispatch by improved ant colony search algorithm[J]. Electric Power Systems Research, 1999, 52(2): 115-121.

[7] SU C, CHIANG C. An incorporated algorithm for combined heat and power economic dispatch[J]. Electric Power Systems Research, 2004, 69(2-3): 187-195.

[8] BASU M. Combined heat and power economic emission dispatch using nondominated sorting genetic algorithm- II[J]. International Journal of Electrical Power & Energy Systems, 2013, 53: 135-141.

[9]  KHORRAM E, JABERIPOUR M. Harmony search algorithm for solving combined heat and power economic dispatch problems[J]. Energy Conversion and Management, 2011, 52(2): 1550-1554.

[10] BASU M. Bee colony optimization for combined heat and power economic dispatch[J]. Expert Systems with Applications, 2011, 38(11): 13527-13531.

[11] NOMAN N, IBA H. Differential evolution for economic load dispatch problems[J]. Electric Power Systems Research, 2008, 78(8): 1322-1331.

[12] SADAT HOSSEINI S S, JAFARNEJAD A, BEHROOZ A H, et al. Combined heat and power economic dispatch by mesh adaptive direct search algorithm[J]. Expert Systems with Applications, 2011, 38(6): 6556-6564.

[13] NIKNAM T, MOJARRAD H D, MEYMAND H Z. A novel hybrid particle swarm optimization for economic dispatch with valve-point loading effects[J]. Energy Conversion and Management, 2011, 52(4): 1800-1809.

[14] MOHAMMADI-IVATLOO B, MORADI-DALVAND M, RABIEE A. Combined heat and power economic dispatch problem solution using particle swarm optimization with time varying acceleration coefficients[J]. Electric Power Systems Research, 2013, 95: 9-18.

[15] MOHAMMADI-IVATLOO B, RABIEE A, SOROUDI A, et al. Iteration PSO with time varying acceleration coefficients for solving non-convex economic dispatch problems[J]. International Journal of Electrical Power & Energy Systems, 2012, 42(1): 508-516.

[16] MENG A, CHEN Y, YIN H, et al. Crisscross optimization algorithm and its application[J]. Knowledge-Based Systems, 2014, 67: 218-229.

[17] ABDOLMOHAMMADI H R, KAZEMI A. A Benders decomposition approach for a combined heat and power economic dispatch[J]. Energy Conversion and Management, 2013, 71: 21-31.

[18] BAHMANI-FIROUZI B, FARJAH E, SEIFI A. A new algorithm for combined heat and power dynamic economic dispatch considering valve-point effects[J]. Energy, 2013, 52: 320-332.

[19] SASHIREKHA A, PASUPULETI J, MOIN N H, et al. Combined heat and power (CHP) economic dispatch solved using Lagrangian relaxation with surrogate subgradient multiplier updates[J]. International Journal of Electrical Power & Energy Systems, 2013, 44(1): 421-430.

[20] 王欣, 秦斌, 阳春华, 等. 基于混沌遗传混合优化算法的短期负荷环境和经济调度[J]. 中国电机工程学报, 2006, 26(11): 128-133.

WANG Xin, QIN Bin, YANG Chunhua, et al. Short term environmental/economic generation scheduling based on chaos genetic hybrid optimization algorithm[J]. Proceedings of the CSEE, 2006, 26(11): 128-133.

[21] ROY P K, PAUL C, SULTANA S. Oppositional teaching learning based optimization approach for combined heat and power dispatch[J]. Electrical Power and Energy Systems, 2014, 57: 392-403.

[22] ZHU Y, WANG J, QU B. Multi-objective economic emission dispatch considering wind power using evolutionary algorithm based on decomposition[J]. International Journal of Electrical Power & Energy Systems, 2014, 63: 434-445.

[23] 方景辉, 温镇. 分布式光伏就地自适应电压控制策略研究[J]. 电力系统保护与控制, 2015, 43(23): 49-55.

FANG Jinghui, WEN Zhen. Research on local adaptive voltage control strategy based on distributed PV[J]. Power System Protection and Control, 2015, 43(23): 49-55.

[24] BILIL H, ANIBA G, MAAROUFI M. Probabilistic economic/environmental power dispatch of power system integrating renewable energy sources[J]. Sustainable Energy Technologies and Assessments, 2014, 8: 181-190.

[25] 何宇斌, 文云峰, 戴赛, 等. 基于故障风险指标排序的安全约束最优潮流[J]. 电力系统保护与控制, 2015, 43(13): 52-59.

HE Yubin, WEN Yunfeng, DAI Sai, et al. Security- constrained optimal power flow based on risk ranking of contingencies[J]. Power System Protection and Control, 2015, 43(13): 52-59.

(编辑 张爱琴)

Crisscross optimization algorithm for combined heat and power economic dispatch

MENG Anbo, MEI Peng, LU Haiming

(School of Automation, Guangdong University of Technology, Guangzhou 510006, China)

A method based on crisscross optimization algorithm (CSO) is introduced to solve combined heat and power economic dispatch (CHPED) problem. CSO adopts a double-crisscross search mechanism, introducing expand factor to increase global search ability in horizontal crisscross, introducing the concept of dimension-crisscross in vertical crisscross, to avoid falling into dimension local optima. The CSO implements global parallel search, which can effectively accelerate the convergence rate. The proposed method is illustrated for a 48-units system that contains power-only units, cogeneration units and heat-only units, with which the model of CHPED problem is established. The simulation results show that the proposed algorithm is feasible and effective in solving the CHPED problem, providing a better method for the actual scheduling system.

cogeneration; economic load dispatch; crisscross optimization algorithm; dimension local optima; parallel search

10.7667/PSPC150890

2015-05-28；

2015-11-12

孟安波(1971-)，男，博士，副教授，主要研究方向为电力系统自动化、系统分析与集成；E-mail: mp512@qq.com梅 鹏(1990-)，男，通信作者，硕士研究生，主要研究方向为电力系统调度、智能算法在电力系统中的应用；E-mail: meipeng001@qq.com 卢海明(1990-)，男，硕士研究生，主要研究方向为智能算法在电力系统中的应用。E-mail: mp721@qq.com