双馈风电机组对接入区域系统暂态功角稳定性的影响分析

刘斯伟，李庚银，周 明



双馈风电机组对接入区域系统暂态功角稳定性的影响分析

刘斯伟，李庚银，周 明

(新能源电力系统国家重点实验室(华北电力大学)，北京 102206)

系统惯性中心的动态行为可以有效地反映系统的整体动态趋势。基于系统惯性中心的动态数学模型，推导了双馈风电机组(Doubly Fed Induction Generator, DFIG)接入后的系统惯性中心运动方程。并通过分析DFIG接入对系统惯性中心运动方程中关键因素的影响，揭示了DFIG以不同方式接入系统时对系统惯性中心功角加速度暂态响应的影响机理。当DFIG直接接入系统时，系统惯性中心的暂态功角加速度的变化趋势主要取决于DFIG的接入容量和暂态功率响应特性。当DFIG等容替代同步发电机组接入系统时，DFIG的暂态功率响应和被替代同步发电机组的功率和惯量在原系统中的比重大小将共同决定系统惯性中心的暂态功角加速度的变化情况。仿真结果验证了理论分析的有效性和正确性。

双馈风电机组(DFIG)；系统惯性中心；暂态功角稳定性；功角加速度；影响机理

0 引言

当今由于能源危机、环保压力以及风电制造技术的迅速发展，风力发电在世界范围内得到了高度重视，在我国，风力发电主以大规模集中的方式并入电网，远离负荷中心，传输距离较远[1-3]。双馈风电机组(Doubly Fed Induction Generator，DFIG)因其变速运行范围宽、变流器容量小等优点，成为我国风电场中应用最广泛的风力发电机型[4-5]。通过引入背靠背的双PWM(Pulse Width Modulation)变流器组实现交流励磁控制，DFIG的转速与系统频率实现了机电解耦，并且DFIG的动态响应特性将主要取决于变流器的控制策略。DFIG与传统同步发电机组在工作原理上的区别使其具有不同的动态行为特征，随着其装机容量的不断增长，如何准确分析并网DFIG对系统暂态稳定性的影响成为风电发展的一个难题[6-11]。

很多文献关于DFIG对接入系统暂态稳定性的影响展开了研究[12-18]，文献[15]基于CIGRE 39节点系统模型对DFIG替代同步发电机组的情况进行了仿真，通过比较系统的极限切除时间(Critical Cut Time，CCT)，指出DFIG替代同步发电机组可以提高系统的鲁棒性。文献[16]考虑DFIG的并网接入点位置、联络线阻抗比和接入容量比作为对比条件，通过比较系统内任意同步发电机组间的最大功角差，指出DFIG对系统内同步发电机组暂态稳定性的影响既可能是正面也可能是负面的。文献[17]则研究了DFIG与系统中同步电机的交互作用，认为DFIG可能对电力系统稳定性不利。文献[18]通过建立含DFIG的电力系统暂态能量函数(Transient Energy Function, TEF)，从系统整体的角度分析，经不同仿真条件的计算比较，认为同步发电机组接入相较于DFIG接入时，系统拥有更高的暂态稳定性。在关于DFIG对系统暂态稳定性影响的研究中，以往文献基于不同的研究方法和系统模型开展了大量仿真算例和实例分析，然而得出的结论并不完全一致，虽然大部分研究并对仿真结果进行了详细分析，然而仍未能有效地指出DFIG对接入系统暂态稳定性的本质影响机理。

系统惯性中心(Center of Inertia, COI)的思想广泛应用于电力系统的暂态稳定性分析[19]，其功角和转速的动态方程能够有效反映区域系统的整体动态稳定趋势。本文基于系统惯性中心的动态数学模型，对DFIG接入后的系统惯性中心运动方程进行了推导，并通过分析DFIG接入对运动方程中关键因素的影响方式，深入研究了系统惯性中心功角角速度的暂态变化的影响机理。最后应用时域仿真对理论分析进行有效验证。

1  系统惯性中心动态模型

系统的惯性中心可以被描述为系统内所有同步发电机的实时功角和转速以转动惯量为权重的加权平均值，定义为[20]

其中，

(2)

系统惯性中心的运动方程可以表示为

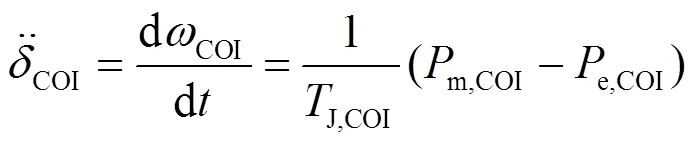
其中，

(4)

2  DFIG对系统暂态功角稳定性的影响

2.1 含DFIG的系统惯性中心动态模型

在传统电力系统的暂态过程中，各同步发电机组的功角和转速通过彼此间的电气联系相互牵制、相互影响，共同维持着系统的暂态功角稳定。而DFIG的励磁控制过程中实现了机电解耦，不具备类似于同步发电机的功角特性和惯量特性，这使得DFIG既不存在功角失稳机制，也无法直接参与同步发电机组之间的互同步稳定机制。

因此当DFIG接入系统后，系统惯性中心的运动方程仍由系统内所有同步发电机的运动方程构成，表示为

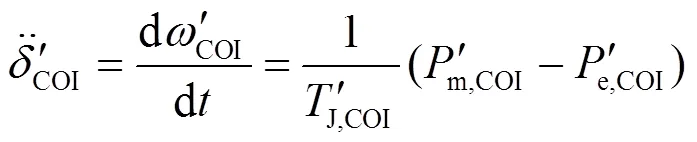
式中，上标“＇”表示DFIG接入后系统各电气量的状态。

式(5)中，DFIG接入后系统惯性中心的惯性时间常数、电磁功率和机械功率将发生以下改变。

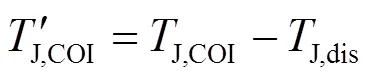
式中，下标“dis”表示被替代同步发电机组的相关变量。

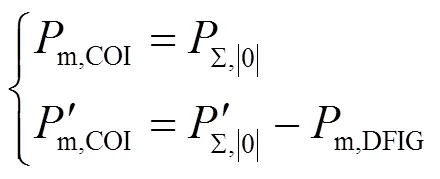
式中，下标“|0|”表示电气量的稳态值。

2.2 DFIG对系统暂态功角稳定性的影响

本节进一步分析当DFIG直接接入系统或替代同步发电机组接入系统情况下，DFIG对系统暂态功角稳定性的影响机理。式(3)和式(5)分别描述了DFIG接入前后系统惯性中心的功角加速度，令表示两者的差值，则有：

式(11)描述了DFIG接入后系统惯性中心功角加速度动态响应的变化情况，下面结合DFIG的不同接入方式展开分析。

(1) DFIG直接接入系统，系统的总负荷不变，同步发电机组数量不变，部分机组减发。此时系统惯性中心的惯性时间常数在DFIG接入系统前后保持不变，即

首先将式(7)、式(8)和式(10)代入式(9)，得到系统惯性中心功角加速度的变化为

(11)

考虑到系统的总负荷不变，同时假设DFIG的接入对系统暂态电压稳定性影响极小可忽略不计，即系统负荷的动态响应影响保持基本不变，则DFIG接入前后系统的总功率需求将满足：

将式(12)进一步代入式(11)，得到系统惯性中心功角加速的变化为

(13)

分析式(13)可知，当DFIG直接接入系统时，系统惯性中心的暂态功角加速度的增减变化将主要取决于DFIG的接入容量和其暂态功率响应特性。

(2) DFIG以等容量替代同步发电机组的方式接入系统，系统的总负荷不变，同步发电机组数量减少。设此时被替代的同步发电机组的惯性时间常数和机械功率分别为

将式(14)代入式(6)，可得系统惯性中心的惯性时间常数为

(15)

由于系统的总负荷不变，即系统内所有发电机机械功率不变，根据式(14)可得DFIG和系统惯性中心的机械功率为

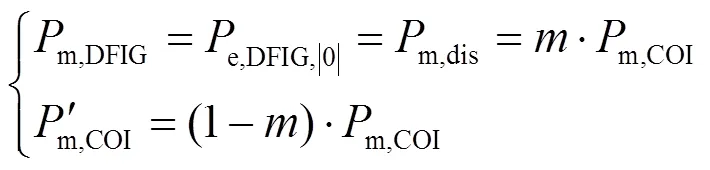
在此基础上，假设通过采取无功补偿措施，使DFIG的接入对系统暂态电压稳定性影响极小可忽略不计，从而保证系统负荷的动态响应维持不变，则对系统总功率需求的描述仍然满足式(12)。

将式(7)、式(8)、式(12)、式(15)和(16)代入式(9)，可得系统惯性中心功角加速度的变化为

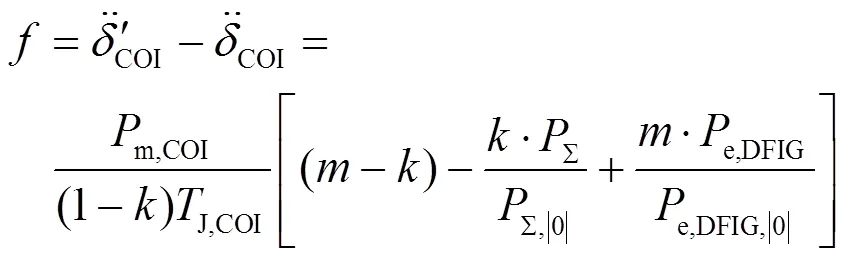
为进一步梳理式(17)的结构，定义：

(18)

式中，下标“p.u.”表示相关变量以自身故障前稳态值为基准的标幺值。

将式(18)代入式(17)，则DFIG替代同步发电机组接入系统后，系统惯性中心功角加速度的变化可以进一步表达为

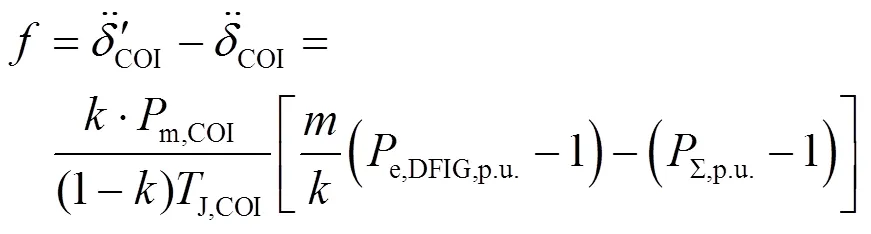
分析式(19)，令：

(20)

和以标幺值形式分别表示了系统总功率需求和DFIG输出功率的暂态响应与自身稳态值的差值。由此可以得到，当DFIG替代同步发电机组接入系统且不影响系统的暂态电压稳定性时，系统惯性中心的暂态功角加速度的增减变化将共同取决于DFIG的暂态功率响应，和被替代同步发电机的功率和惯量在原系统中的比重大小。

3  算例分析

3.1 算例系统

为了验证上述关于DFIG对接入系统暂态功角稳定性的影响分析，基于PSCAD/EMTDC仿真平台搭建了IEEE-3机9节点仿真系统用于算例分析，如图1所示。

图1 IEEE-3机9节点系统示意图

系统中的3台发电机初始均由同步发电机组表示，配有调速器模型和励磁系统模型；负荷均采用恒阻抗模型；同步发电机组和负荷的详细参数如表1和表2所示。接入系统的DFIG风电场模型采用加权等值的方法，用1台详细的DFIG模型表示。系统4 s时于BUS6节点发生三相对称短路故障，持续0.15 s后故障切除。基于本文的研究目的，暂态过程中假设风速保持额定风速12 m/s不变。

表1 IEEE-3机9节点系统发电机数据

表2 IEEE-3机9节点系统负荷数据

3.2 DFIG直接接入系统

DFIG风电场分别以30 MW和60 MW的额定容量接入至BUS9节点，系统中的同步发电机组不被替代，并保持系统中负荷不变。图2展示了两组不同容量DFIG风电场直接接入系统后，系统故障情况下DFIG电磁功率和机械功率的差值以及系统惯性中心功角加速度变化情况，图2(a)中为DFIG电磁功率和机械功率的差值，有。

图2 DFIG直接接入时的系统暂态响应

由图2可见，故障期间，系统惯性中心的功角转速处于加速状态，DFIG电磁功率和机械功率的差值为负；系统惯性中心的功角转速处于减速状态，DFIG电磁功率和机械功率的差值为正。相对应的，根据式(13)，可以看到随着DFIG接入容量的增加，的绝对值增大，而系统惯性中心的功角转速加速度减小，功角转速在故障期间的加速过程和故障后的减速过程都更为缓慢。

3.3 DFIG替代同步发电机组接入系统

DFIG风电场分别以替代同步发电机组GEN1和GEN3的方式接入系统，系统负荷保持不变：

CASE A：DFIG风电场等容量替代同步发电机组GEN1，配置合适容量的静态无功补偿器(static VAR compensator SVC)对DFIG并网点提供暂态电压支撑，保证系统的暂态电压稳定性不改变。

CASE B：DFIG风电场等容量替代同步发电机组GEN3，同样配置合适容量的SVC，保证系统的暂态电压稳定性不改变。

图3和图4分别展示了DFIG风电场替代同步发电机组GEN1和GEN3情况下的系统暂态响应和惯性中心功角加速度的暂态变化趋势。

图3 DFIG替代GEN1时的系统暂态响应

图4 DFIG替代GEN3时的系统暂态响应

根据式(17)和式(18)可知，当DFIG替代同步发电机组接入系统时，系统惯性中心功角加速度的增减与否取决于式(17)中(/)–的正负号；变化幅度的大小则同时受影响于被替代同步发电机组的不同惯性时间常数。由图3(a)、3(b)和图4(a)、4(b)可以看到(/)、和(/)–的暂态变化趋势：故障期间，两组仿真的(/)–均小于零，此时系统惯性中心功角处于加速阶段，因此增速加速度减小；故障切除后，系统惯性中心功角开始减速，在前0.3 s内，CASE A的(/)–小于零，而CASE B的(/)–大于零，因此系统惯性中心功角的暂态响应分别有如图3(c)和图4(c)的变化趋势。

4  结论

双馈风电机组既不存在功角失稳机制，也无法直接参与同步发电机组之间的互同步稳定机制。本文基于系统惯性中心的动态数学模型，推导了双馈风电机组接入后的系统惯性中心运动方程，并通过分析双馈风电机组接入对系统惯性中心运动方程中关键因素的影响，揭示了双馈风电机组以不同接入方式系统时，对系统惯性中心的暂态功角加速度的影响机理。

当双馈风电机组直接接入系统时，系统惯性中心功角加速度的暂态变化趋势主要取决于双馈风电机组的接入容量和其暂态功率响应特性；当双馈风电机组以等容替代同步发电机组的方式接入系统时，双馈风电机组的暂态功率响应情况和被替代同步发电机组的功率和惯量在原系统中的比重大小将共同决定系统惯性中心功角加速度的暂态变化。本文工作对于进一步研究双馈风电机组接入对区域系统间暂态功角稳定性具有重要帮助。

[1] JIANG Liping, CHI Yongning, QIN Haiyan, et al. Wind energy in China[J]. IEEE Power and Energy Magazine, 2011, 9(6): 36-46.

[2] 王境彪, 希望∙阿不都瓦依提, 晁勤, 等. 双馈风电场接入交流或交直流混合系统低频振荡模态对比分析[J]. 电力系统保护与控制, 2015, 43(13): 23-29.

WANG Jingbiao, XI Wang∙Abuduwayiti, CHAO Qin, et al. Modal contrastive analysis of the low-frequency oscillation of AC and AC/DC hybrid system integrated by DFIG-based wind farms[J]. Power System Protection and Control, 2015, 43(13): 23-29.

[3] 齐尚敏,李凤婷,何世恩,等. 具有低电压穿越能力的集群接入风电场故障特性仿真研究[J].电力系统保护与控制,2015,43(14): 55-62.

QI Shangmin, LI Fengting, HE Shien, et al. Research on fault characteristics of grid-connected large scale wind farms with LVRT capability[J]. Power System Protection and Control, 2015, 43(14): 55-62.

[4] PENA R, CLARE J C, ASHER G M. Doubly fed induction generator using back-to-back PWM converters and its application to variable-speed wind-energy generation[J]. Electric Power Applications, 1996, 143(3): 231-241.

[5] 冯双磊, 赵海翔, 任普春, 等. 基于PSCAD/EMTDC的双馈式变速恒频风电机组动态模型仿真[J]. 电网技术, 2007, 31(17): 30-35.

FENG Shuanglei, ZHAO Haixiang, REN Puchun, et al. PSCAD/EMTDC based simulation study on dynamic model of doubly-fed variable speed wind turbine[J]. Power System Technology, 2007, 31(17): 30-35.

[6] 李岩松,郭世繁,任国威. 双馈式风力发电系统的机电暂态建模与运行分析[J].电力系统保护与控制, 2013, 41(13): 101-109.

LI Yansong, GUO Shifan, REN Guowei. Modelling and operation simulation of doubly-fed type wind power generation system electromechanical transient model[J].Power System Protection and Control, 2013, 41(13): 101-109.

[7] 秦超,刘艳丽,余贻鑫,等.含双馈风机电力系统的动态安全域[J]. 电工技术学报, 2015, 30(18): 157-163.

QIN Chao, LIU Yanli, YU Yixin, et al. Dynamic security region of power systems with double fed induction generator[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 157-163.

[8] 王振树, 刘岩, 雷鸣, 等. 基于Crowbar的双馈机组风电场等值模型及并网仿真分析[J]. 电工技术学报, 2015, 30(4): 44-51.

WANG Zhenshu, LIU Yan, LEI Ming, et al. Doubly-fed induction generator wind farm aggregated model based on Crowbar and integration simulation analysis[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 44-51.

[9] 林俐, 杨以涵. 基于扩展等面积定则的含大规模风电场电力系统暂态稳定性分析[J]. 电力系统保护与控制, 2012, 40(12): 105-110.

LIN Li, YANG Yihan. Analysis of transient stability of power system including large scale wind power based on the extended equal area rule[J]. Power System Protection and Control, 2012, 40(12): 105-110.

[10] 孙勇, 陈晨, 王瑞明, 等. 电压两次跌落对双馈型风电机组的影响分析[J]. 电网与清洁能源, 2013, 29(8): 109-112.

SUN Yong, CHEN Chen, WANG Ruiming, et al. Impacts on DFIG wind turbine during the voltage double-dip[J]. Power System and Clean Energy, 2013, 29(8): 109-112.

[11] 刘铖, 蔡国伟, 杨德友, 等. 计及风机无功约束的电压稳定性分析[J]. 电力系统及其自动化学报, 2013, 25(1): 1-6.

LIU Cheng, CAI Guowei, YANG Deyou, et al. Analysis of voltage stability considering reactive power limitation of wind turbine[J]. Proceedings of the CSU-EPSA, 2013, 25(1): 1-6.

[12] 李东东, 梁自超, 周玉琦. 含风电场的受端系统暂态电压稳定性评估[J]. 电力系统保护与控制, 2015, 43(13): 8-14.

LI Dongdong, LIANG Zichao, ZHOU Yuqi. Transient voltage stability assessment of receiving end grid incorporating with wind farm[J]. Power System Protection and Control, 2015, 43(13): 8-14.

[13] HAO Zhenghang, YAO Zhiqing, LI Shaohua, et a1. The contribution of double-fed wind farms to transient voltage and damping of power grids[J]. Tehnicki Vjesnik-Technical Gazette, 2015, 22(1): 43-49.

[14] 时锐, 焦然, 陈艳霞. 含大规模风电电网的静态电压仿真分析[J]. 高压电器, 2014, 50(12): 105-109.

SHI Rui, JIAO Ran, CHEN Yanxia. Static voltage simulation analysis of grid with large-scale wind power[J]. High Voltage Apparatus, 2014, 50(12): 105-109.

[15] LIN Li, HOU Hongjing, Li Wenxia, et al. Simulation and comparison of transient stability of power system includingDFIGs wind farm based on detailed model[C] // Sustainable Power Generation and Supply, Nanjing, 2009: 1-6.

[16] SHI Libao, DAI Shiqiang, NI Yixin, et al. Transient stability of power systems with high penetration of DFIG based wind farms[C] // Power & Society General Meeting, Calgary, 2009: 1-6.

[17] 郝正航, 余贻鑫, 曾沅. 双馈风力发电机功角暂态行为及其控制策略[J]. 电力自动化设备, 2011, 31(2): 79-83.

HAO Zhenghang, YU Yixin, ZENG Yuan. Transient performance of DFIG power angle in wind farm and its control strategy[J]. Electric Power Automation Equipment, 2011, 31(2): 79-83.

[18] CHOWDHURY M A, HOSSEINZADEH N, SHEN W X, et al. Comparative study on fault responses of synchronous generators and wind turbine generators using transient stability index based on transient energy function[J]. International Journal of Electrical Power & Energy Systems, 2013, 51(10): 145-152.

[19] KUNDUR P. Power system stability and control[M]. New York, USA: Mc Graw Hill, Inc, 1992: 461.

[20] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京:清华大学出版社, 2002: 186.

(编辑 葛艳娜)

Impact analysis of doubly-fed induction generator on the transient angle stability of the region with wind power integrated

LIU Siwei, LI Gengyin, ZHOU Ming

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)

The dynamic motion of system center of inertia (COI) can effectively indicate the general trend of a power system dynamics. Based on this, the developed COI dynamic model considering integrated doubly-fed induction generators (DFIGs) is proposed. With the impacts of DFIGs on the key factors in COI dynamic motions deduced, the influence mechanism of DFIGs on the power angle accelerating speed (PAAS) of system COI is then deeply investigated. If DFIGs are integrated without displacing synchronous generators, the change in PAAS of system COI is mainly determined by the capacity and transient power response of integrated DFIGs. And when synchronous generators are displaced, the change in PAAS of system COI is affected jointly by the DFIG transient power response and the proportions of the inertia and capacity of displaced synchronous generators in the origin system.The theoretical analysis is effectively verified and illustrated by simulation studies. This work is supported by the Major Program of the National Natural Science Foundation of China (No. 51190103) and the “111” Project (No. B08013).

doubly-fed induction generator (DFIG); system center of inertia (COI); transient angle stability; power angle accelerating speed; influence mechanism

10.7667/PSPC151725

国家自然科学基金重大项目课题(51190103)；高等学校学科创新引智计划项目(B08013)

2015-09-25；

2015-11-17

刘斯伟(1988-)，男，博士，研究方向为双馈风电机组的建模与控制、风电接入对系统暂态稳定性的影响分析；E-mail: liusw@necpu.edu.cn 李庚银(1964-)，男，博士，教授，博士生导师，主要研究方向为新能源电力系统分析与控制，先进输变电技术，电能质量等；E-mail: ligy@ncepu.edu.cn 周 明(1967-)，女，博士，教授，博士生导师，主要研究方向为新能源电力系统分析与控制，电力市场，电能质量等。E-mail: zhouming@ncepu.edu.cn