考虑多因素关联适用于大系统仿真的风电场暂态模型选取方法

林 俐，张凌云，赵 双，朱浩骏，余梦泽



考虑多因素关联适用于大系统仿真的风电场暂态模型选取方法

林 俐1，张凌云1，赵 双2，朱浩骏3，余梦泽3

(1.新能源电力系统国家重点实验室(华北电力大学)，北京 102206；2.广东电网公司东莞供电局， 广东 东莞 523000；3.广东电网公司电网规划研究中心，广东 广州 510080)

选择合适的风电场暂态模型是进行风电并网动态和稳定仿真分析的基础。首先从风电场装机容量、风电场并网点位置、风电场类型和场内机组的排列方式4个方面分析了风电场暂态模型选取时需要考虑的影响因素。然后面向大系统仿真，提出了满足差异性评价指标要求的，风电场不同暂态模型的选取阈值计算方法。进而给出了风电场暂态模型选取的实用准则。最后采用某实际地区电网数据验证了所提方法的有效性。

风电场；暂态模型；模型选取；系统仿真；差异性指标

0 引言

随着风电技术的不断成熟和国家可再生能源政策的实施，我国风力发电建设已进入了一个快速发展的时期。大规模风电并网带来了许多亟待解决的问题，如局部的电能质量问题、电压水平下降、线路传输功率越限、系统短路容量增加，由于大多数规模化、集群化风电场都远离负荷中心，与主网联系薄弱，可能造成系统全局暂态稳定性的改变等[1-3]，给电力系统的安全稳定运行带来安全隐患。因此，在现有大电网仿真的基础上，需对风电场暂态模型的建立和选取进行研究，为电网仿真提供理论依据。

由于仿真软件的限制，目前在电网暂态计算中，对风电场模型的选取主要有三种方式：第一种是将风电场处理成负荷模型，文献[4]比较负荷模型对含风力发电的综合负荷特性的描述能力，认为随风电机组接入容量增加，风电机组对负荷特性影响力增强，风电机组接入容量比例不大于20%时，负荷模型具有良好的描述风电机组运行特性的能力。第二种是将风电场等值为单机模型，文献[5]指出由于一个风电场内各台风电机组之间的电气联系紧密，在暂态过程中各台风电机组的运行特性十分相似，可采用按容量加权法得到的单机等值模型近似模拟风电场的暂态特性。文献[6]以笼型异步风电场的实际运行数据为样本，提出了基于遗传算法的风电场单机等值建模方法和参数优化模型。仿真结果表明无论对于风电场内机组参数相同还是不同，风电场采用基于遗传算法的单机等值模型具有与采用详细模型时相似的动态特性。第三种是将风电场处理成多机等值模型，对于大型风电场，由于地形地貌以及尾流效应和时滞等因素的影响，风电场内风速分布不均匀，风电机组的风速差异较大，使用单机表征法通常会产生较大误差，针对这些问题，文献[7-8]提出了按风速进行机群分类的多机等值方法。文献[9]提出一种适合风速差异较大的、基于K-means聚类算法的定速机组风电场动态等值多机表征方法，并通过仿真验证了方法的有效性。

以上研究大都是针对具体的仿真网络验证所提方法以及等值模型的准确性，并没有给出在实际系统仿真中选择风电场模型的方法。鉴于此，本文从风电场装机容量、风电场并网点位置、风电场类型和场内机组的排列方式4个方面分析了风电场暂态模型选取需要考虑的影响因素，然后面向大系统仿真，提出了满足差异性评价指标要求的，风电场不同暂态仿真模型的阈值计算方法，进而给出风电场暂态仿真模型选取的实用准则，最后采用某实际地区电网验证所提方法的有效性。

1  风电场暂态模型选取需要考虑的影响因素

1.1 风电场装机容量

风电场装机容量是模型选取时一个最直接的影响因素。如图1所示的某地区实际系统中，220 kV两英变电站通过联络线1与主网相连，设风电场A是该地区待规划的一座双馈型风电场，当其装机容量分别为15 MW、285 MW、700 MW时，分别采用负荷模型、单机模型、多机模型进行模拟。设风电场的初始风速为9.7 m/s，对于设计的扰动1：=1 s时两英站至红场K0A站一回线50%处发生三相短路故障，=1.2 s时两侧断路器断开，同时=1 s时加入幅值为4 m/s，持续时间为4 s的阵风扰动。

BPA作为电力系统中广泛应用的仿真分析软件，具有仿真规模大、计算速度快等特点。本文采用该软件进行时域仿真，仿真结果如图2~图7所示。

图1 某地区实际电网地理接线图

图2 装机容量为15 MW时两英站电压

图3 装机容量为15 MW时联络线1的有功功率

图4 装机容量为285 MW时两英站电压

图5 装机容量为285 MW时联络线1的有功功率

图6 装机容量为700 MW时两英站电压

由图2~图7可知，当风电场A装机容量较小时，风电场等值模型选取差异对两英变电站220 kV母线电压和联络线1上的功率影响不大，风电场动态对220 kV电网的影响可以忽略不计，此时将风电场直接处理成传统的负荷模型即可；随着风电场装机容量的逐渐增大，风电场采用不同模型时，两英站电压和联络线1功率的仿真结果差异渐趋明显，采用负荷模型模拟风电场已无法描述出风电场对220 kV电网的影响；当风电场A的装机容量增大到700 MW时，风电场采用单机和多机等值模型所得到的两英站电压和联络线1上功率的仿真特性差异比较显著，其中联络线功率误差最大约为39%，采用多机等值模型更能体现风电场内所有机组对故障和阵风扰动的叠加效果。此时，如果对仿真精度要求更高时，需要采用能反映风电机组运行差异的多机等值模型来表征风电场。

图7 装机容量为700 MW时联络线1的有功功率

需要注意的是，对于不同的待研究电网而言，相同规模的风电场选取的模型也可能不一样。比如，对于同一风电场，当待研究电网为220 kV主网时可等值为单机模型，而对于500 kV主网则等值为负荷模型。

1.2 风电场类型

当风电场是由多种类型机组组成的混杂风电场时，由于不同类型的风电机组表现出来的动态特性各不相同[10-11]，此时需要考虑机组的动态差异。

下面以普通异步风电机组(FSIG)、双馈风电机组(DFIG)混杂风电场进行讨论，定义FSIG装机容量占整个风电场总装机容量的比值为风电场的混杂度。

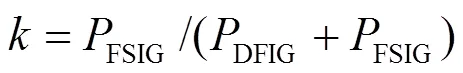
这里仍以图1所示的地区电网为研究系统，设风电场A为400 MW的FSIG、DFIG混杂风电场，分别取=0.05、=0.1、=0.3，当风电场采用负荷、单机和多机模型时，在扰动1下的仿真结果如图8所示。其中单机模型为不考虑风电场内的机组类型差异，将风电场等值为单DFIG模型；多机模型为考虑了FSIG和DFIG的动态特性的双机等值模型[9]。

图8 k值不同时采用三种模型的仿真结果

所以，对于一个大容量的混杂风电场，当混杂度较小时，可不考虑风电场机型差异，用主导机型表示的单机等值模型模拟混杂风电场；而当风电场混杂度较高时，不能忽略不同类型机组的动态特性，需要采用能反应出混杂风电场特性的多机等值模型。

1.3 风电场并网点的位置

并网点的位置也是影响风电场暂态模型选取的一个重要因素。当风电场离研究电网较远时，可以忽略风电场动态特性。例如对于待研究的220 kV电网而言，远离该电网、且接入35 kV或10 kV的风电场对电网动态特性影响微乎其微，可以将风电场直接用负荷模拟。当风电场离待研究电网较近时，需要考虑风电场动态对电网的影响，此时需采用能反映风电场动态特性的单机或多机模型来进行表征。例如对图1所示系统中的110 kV及以下电网动态特性进行研究时，已不能采用负荷模型模拟风电场。这是由于风电场所处网络末端的无功往往出现不足，节点电压对风电注入功率的变化会较敏感，风电场动态对局部电网的电压质量和电压稳定性的影响也会比较大[12]，采用恒功率或恒阻抗表示的负荷模型显然表现不出这种风电场动态对电网的影响。特别地，当需要模拟电网发生某些极端故障时风机的脱网特性，若风电场仍采用负荷模型模拟，必然不能表征风电场低电压穿越特性，所得到的仿真结果会与实际情况产生较大误差。

1.4 风电场机组排列方式

当待模拟的大容量风电场距离研究电网较近，需要计及风电场动态特性时，场内机组的排列方式也是影响风电场暂态模型选取的重要因素。

通常，场内风电机组的排列和风速分布是风电场机群划分的主要依据。文献[13-16]中利用了能反映风电机组运行点的转速、风速、实测有功作为机群分类指标，以风电机组具有相同或相近的运行点为机群划分原则，将具有相同运行点的风电机组划分为一个机群，建立风电场的多机表征模型，较准确地反映了风电场动态响应特性。

2  风电场暂态模型选取方法

2.1 差异性评价指标

为了考察风电场采用不同模型时仿真结果差异性大小，定义以下两种差异性评价指标：

当满足以下任一条件时，则认为风电场模型会对仿真结果有较大影响：

2.2 以风电场装机容量选择模型

为了考察风电场采用不同模型时仿真结果差异性大小，定义以下两种差异性评价指标：

图9 典型电网连接示意图

2.3 大容量混杂风电场的模型选择

当风电场为混杂风电场时，混杂度在不同范围时应采用不同的等值模型。此处仍引用1.2节中混杂度的定义，设，其中比例较少的一类风电机组装机容量为，另一类风电机组的装机容量为。

给定电网以及误差要求，可以确定一个片区内混杂风电场的混杂度阈值。当小于时，采用以主导机型表示的单机等值模型模拟混杂风电场；当大于时，采用考虑机型差异的多机等值模型模拟混杂风电场。

这里同样以图9所示的待模拟的混杂风电场为例说明混杂度阈值的确定。已知片区1的、，当超过时且在2.2节中设置的故障扰动下，考察风电场采用单机等值模型和多机等值模型时联络线上有功功率和母线电压的变化情况，计算相应的、，则存在使得：

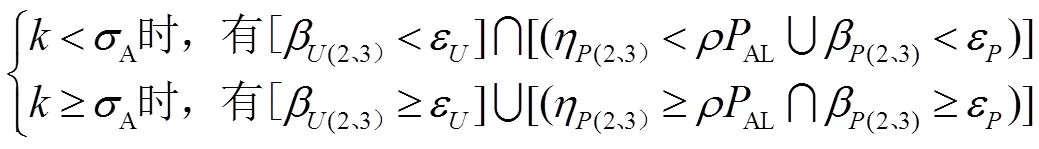
2.4 计及并网点位置的模型选择

为了量化并网点的位置对风电场暂态模型选取的影响，定义为

2.5 风电场模型选取实用准则

a. 风电场内机组类型相同，将风电场等值成一台同类型风电机组。

1) 风电场内机组类型相同。按风电机组的排列方式进行多机等值：

a. 若风电场地势平坦，机组排列较规律，则直接按列进行等值，若列数过多，此时可考虑将相邻的某几列风电机组等值为一台风电机组，适当地减少等值风电机组的台数。

b. 若风电场地形较复杂，场内各风电机组的风速差异性较大，此时，可以采用聚类算法进行机群划分。利用能反映风电机组运行点的转速、风速、实测有功等作为机群分类指标，以风电机组具有相同或相近的运行点为机群划分原则，将具有相同运行点的风电机组划分为一个机群，并分别用一台风电机组等值一个机群，建立风电场的多机表征模型。

3  实证仿真

本节以图1所示实际系统220 kV主网为待研究电网，该地区电网的总有功负荷=3 000 MW，片区1内的有功负荷=280 MW。误差要求、、分别取为5%、25%、15%。

风电场A装机容量不同时，系统在扰动1下的部分计算结果见表1~表4，表中、、分别指仿真结果差异最大时刻风电场采用负荷模型、单机模型、多机模型时两英站的电压，、、分别指仿真结果差异最大时刻采用三种模型时联络线1的有功功率。

表1 两英站电压及相应的值

Table 1 Liangying substation voltage and corresponding value of

CPW/MWU1/p.u.U2/p.u. 0.45%13.51.0471.0490.2% 4.5%1351.0501.0722.1% 7.2%2151.0441.0995.0% 9.5%2851.0361.0935.2% 14.2%4261.0231.1107.8% 16.7%5001.0111.1149.2% 19.0%5700.9961.11810.9% 21.5%6450.9761.12112.9%

表2 两英站电压及相应的值

Table 2 Liangying substation voltage and corresponding value of

表2 两英站电压及相应的值

CPW /MWU2/p.u.U3/p.u. 0.45%13.51.0491.0490% 4.5%1351.0721.0720% 7.2%2151.0991.0990% 9.5%2851.0931.0930% 14.2%4260.9951.0051.0% 16.7%5000.9750.9881.35% 19.0%5700.9510.9681.76% 21.5%6450.9280.9593.23%

表3 联络线1有功功率及相应的和值

Table 3 Active power of tie line 1 and corresponding value of and

表3 联络线1有功功率及相应的和值

CP1 /MWP2 /MW 0.45%10.511.61.19.5% 4.5%90.699.48.68.6% 7.2%151.0164.113.18.0% 9.5%200.0219.819.89.0% 14.2%300.0444.2144.232.4% 16.7%345.1530.4185.334.9% 19.0%390.7607.2216.535.7% 21.5%435.2686.2251.036.6%

表4 联络线1有功功率及相应的和值

Table 4 Active power of tie line 1 and corresponding value of and

表4 联络线1有功功率及相应的和值

CP2/MWP3/MW 0.45%11.611.90.32.5% 4.5%99.4103.74.34.1% 7.2%164.1170.05.93.4% 9.5%219.8229.59.74.2% 14.2%444.2392.651.613.1% 16.7%530.4460.170.315.2% 19.0%607.2526.780.515.2% 21.5%686.2571.5114.720.1%

对于选定的实际地区电网，在研究220 kV电网的动态和稳定特性时，对于大部分现有的装机容量为49.5 MW及以下的风电场，均可直接等值为负荷模型，部分装机容量较大的风电场一般采用单机模型即能够满足系统仿真需求。目前该电网尚无需要多机等值的风电场。

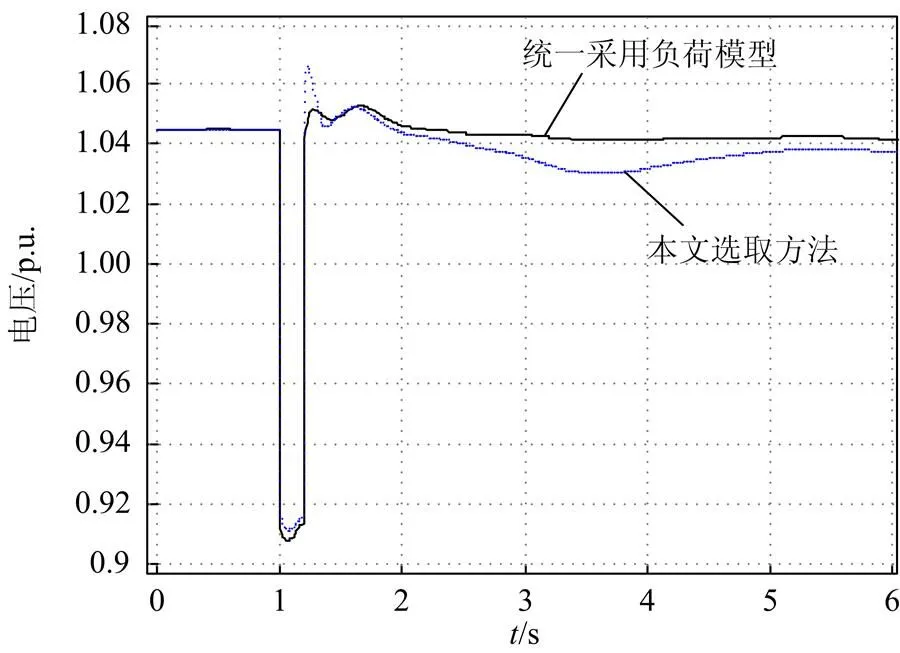
图10 风电场模型差异时两英站电压对比

图11 风电场模型差异时联络线1有功功率对比

4  结论

本文从风电场装机容量、风电场并网点位置、风电场类型、风电场内机组的排列方式4个方面讨论了风电场暂态模型选取需要考虑的影响因素，然后面向大系统仿真给出了风电场暂态模型选取的方法，最后以某实际地区电网验证了所提方法的有效性，并得到如下结论：

(1) 风电场的装机容量是风电场暂态模型选取最重要的影响因素，当风电场装机容量较小时，可将风电场处理为负荷模型，随着风电场装机容量的增加，宜将风电场处理为单机等值模型或多机等值模型。

(2) 对于选定的实际地区电网，在研究220 kV电网的动态和暂态特性时，大部分50 MW以下的风电场模型可以用负荷模型等值，也即小容量风电场对220 kV及以上电网的动态特性影响基本可以忽略。

(3) 当风电场的装机容量占地区负荷比例超过某一值时，还需要考虑到风电场类型以及场内机组排列方式的影响。当风电场的混杂度较低时，可直接采用单机等值模型，而当混杂度较高时，需要采用能反映出混杂风电场特性的多机模型。对于场内机组排列方式而言，当机组呈规则的矩形方式排列时，可将同行或同列的机组等值为一台风电机组，而对于地形复杂、机组排列不规则的大型风电场，可以按机组具有相近运行点为机群划分原则，采用聚类算法进行机群划分，将同群内的机组合并为一台等值机，建立风电场的多机表征模型。

[1] 迟永宁, 刘燕华, 王伟胜, 等. 风电接入对电力系统的影响[J]. 电网技术, 2007, 31(3): 77-81.

CHI Yongning, LIU Yanhua, WANG Weisheng, et al. Study on impact of wind power integration on power system[J]. Power System Technology, 2007, 31(3): 77-81.

[2] 李东东, 梁自超, 周玉琦. 含风电场的受端系统暂态电压稳定性评估[J]. 电力系统保护与控制, 2015, 43(13): 8-14.

LI Dongdong, LIANG Zichao, ZHOU Yuqi. Transient voltage stability assessment of receiving end grid incorporating with wind farm[J]. Power System Protection and Control, 2015, 43(13): 8-14.

[3] 边晓燕, 耿艳, 李学武, 等. 风电并网系统小干扰概率稳定性分析与改善[J]. 电力系统保护与控制, 2015, 43(20): 1-7.

BIAN Xiaoyan, GENG Yan, LI Xuewu, et al. Probabilistic small-signal stability analysis and improvement of power system with wind farm integration[J]. Power System Protection and Control, 2015, 43(20): 1-7.

[4] 毕正军, 蒋子丹, 李欣然, 等. 考虑风力发电的综合负荷特性及其等效描述[J]. 电力系统及其自动化学报, 2012, 24(1): 8-13.

BI Zhengjun, JIANG Zidan, LI Xinran, et al. Composite load characteristics and its equivalent description based on the impact of wind power[J]. Proceedings of the CSU-EPSA, 2012, 24(1): 8-13.

[5] 雷亚洲, LIGHTBODY G. 国外风力发电导则及动态模型简介[J]. 电网技术, 2005, 29(12): 27-32.

LEI Yazhou, LIGHTBODY G. An introduction on wind power grid code and dynamic simulation[J]. Power System Technology, 2005, 29(12): 27-32.

[6] 李辉, 王荷生, 史旭阳, 等. 基于遗传算法的风电场等值模型的研究[J]. 电力系统保护与控制, 2011, 39(11): 1-8.

LI Hui, WANG Hesheng, SHI Xuyang, et al. Study on equivalent model of wind farms based on genetic algorithm[J]. Power System Protection and Control, 2011, 39(11): 1-8.

[7] FERNÁNDEZ L M, SAENZ J R, JURADO F. Dynamic models of wind farms with fixed speed wind turbines[J]. Renewable Energy, 2006, 31(8): 1203-1230.

[8] AKHMATOV V, KNUDSEN H. An aggregate model of a grid-connected, large-scale, offshore wind farm for power stability investigations-importance of windmill mechanical system[J]. Electrical Power Energy Systems, 2002, 24(9): 709-717.

[9] 米增强, 苏勋文, 杨奇逊, 等. 风电场动态等值模型的多机表征方法[J]. 电工技术学报, 2010, 25(5): 162-169.

MI Zengqiang, SU Xunwen, YANG Qixun, et al. Multi-machine representation method for dynamic equivalent model of wind farms[J]. Transactions of China Electrotechnical Society, 2010, 25(5): 162-169.

[10]张元, 郝丽丽, 戴嘉祺. 风电场等值建模研究综述[J]. 电力系统保护与控制, 2015, 43(6): 138-146.

ZHANG Yuan, HAO Lili, DAI Jiaqi. Overview of the equivalent model research for wind farms[J]. Power System Protection and Control, 2015, 43(6): 138-146.

[11]葛江北, 周明, 李庚银. 大型风电场建模综述[J]. 电力系统保护与控制, 2013, 41(17): 146-153.

GE Jiangbei, ZHOU Ming, LI Gengyin. Review on large-scale wind farm modeling[J]. Power System Protection and Control, 2013, 41(17): 146-153.

[12]王伟胜, 冯双磊, 张义斌. 风电场最大装机容量和电网短路容量的关系[J]. 国际电力, 2005, 9(2): 31-34.

WANG Weisheng, FENG Shuanglei, ZHANG Yibin. The relationship between wind farm maximum capacity and short-circuit capacity of the power grid[J]. International Electric Power for China, 2005, 9(2): 31-34.

[13]陈树勇, 王聪, 申洪, 等. 基于聚类算法的风电场动态等值[J]. 中国电机工程学报, 2012, 32(4): 11-19.

CHEN Shuyong, WANG Cong, SHEN Hong, et al. Dynamic equivalence for wind farms based on clustering algorithm[J]. Proceedings of the CSEE, 2012, 32(4): 11-19.

[14]林俐, 陈迎. 基于扩散映射理论的谱聚类算法的风电场机群划分[J]. 电力自动化设备, 2013, 33(6): 113-118.

LIN Li, CHEN Ying. A wind turbine cluster division method of spectral clustering based on the theory of diffusion maps[J]. Electric Power Automation Equipment, 2013, 33(6): 113-118.

[15]高峰, 赵东来, 周孝信, 等. 直驱式风电机组风电场动态等值[J]. 电网技术, 2012, 36(12): 222-227.

GAO Feng, ZHAO Donglai, ZHOU Xiaoxin, et al. Dynamic equivalent algorithm for wind farm composed of direct-drive wind turbines[J]. Power System Technology, 2012, 36(12): 222-227.

[16]陈迎. 基于运行数据的风电场等效建模研究[D]. 北京:华北电力大学, 2012.

(编辑 葛艳娜)

Selecting approach for transient model of wind farm aiming at system simulation considering correlations among multi-factors

LIN Li1, ZHANG Lingyun1, ZHAO Shuang2, ZHU Haojun3, YU Mengze3

(1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China; 2. Dongguan Power Supply Bureau of Guangdong Power Grid Corporation, Dongguan 523000, China; 3. Power System Planning Research Center of Guangdong Power Grid Corporation, Guangzhou 510080, China)

An appropriate transient model of wind farm is demanded for researches about the impacts of large scale wind generation. Firstly, the influence factors which should be taken into consideration of the transient model selecting for wind farm are investigated in view of four aspects as follows, the installed capacity of wind farm, types of wind farm, the point of interconnection of wind farm and the arrangement of wind turbines. Secondly, the calculation method of threshold selection for different transient models of wind farms for system simulation which meets the requirement of the error evaluation index is proposed and a practical criteria for selecting the transient model of wind farm is presented. Finally, the effectiveness of the proposed method is verified based on an actual regional power grid. This work is supported by National Natural Science Foundation of China — the theory and analysis methods for the large scale wind power integrated random-certainty coupled power system (No. 51190103), and Research and Demonstrationon Key Technology of Combined Operation Control of Multi Energy Power with Large-Scale Photovoltaic Power (No. 2013BAA02B01).

wind farm; transient model; model selection; system simulation; error index

10.7667/PSPC150871

国家自然基金重大项目(随机-确定性耦合电力系统稳定机理及分析方法)(51190103)；国家科技支撑计划项目(含大型光伏电站的多种能源发电联合运行控制关键技术研究及示范)(2013BAA02B01)

2015-05-24；

2015-07-08

林 俐(1968-)，女，博士，副教授，研究方向为电力系统分析与控制、风电并网及其系统分析等；E-mail:linli@ncepu.edu.cn 张凌云(1989-)，男，硕士研究生，研究方向为电力系统分析、运行与控制及风电并网；E-mail: zly897@126.com 赵 双(1989-)，男，硕士，研究方向为新能源电力系统分析与控制。