基于粗糙集理论与D-S证据理论改进的多元回归负荷预测方法研究

陈毅波，郑 玲，姚建刚



基于粗糙集理论与D-S证据理论改进的多元回归负荷预测方法研究

陈毅波1，郑 玲2，姚建刚2

(1.国网湖南省电力公司通信公司，湖南 长沙 410007；2.湖南大学电气与信息工程学院，湖南 长沙 410012)

当前，中长期负荷预测大多采用多元回归算法，但在建模时对影响因子及历史年的选择缺乏良好的依据，很难在考虑更多影响因子及历史年数据与降低回归模型误差之间做出平衡。这使多元回归算法在实际负荷预测中的精准度很不稳定。将粗糙集理论与D-S证据理论引入多元回归算法，利用粗糙集理论对影响因子进行重要性排序。分别以历史年和影响因子为对象进行聚类，以此建立多个多元回归模型。利用D-S证据理论对多个组合预测的权重分配方案进行权重融合，得出最终基于多元回归分析法的组合预测模型。经算例验证，该模型能较好地平衡影响因子和历史年的选取，能有效提高多元回归算法在中长期负荷预测中的准确性，适用性强。

中长期负荷预测；多元回归；粗糙集方法；D-S证据理论

0 引言

电力系统中长期负荷预测中负荷受经济、社会和气象等不确定因素影响较大，如何从多因素中提取关键影响因子和减小多因素综合所带来的不确定性并提高预测结果的精确性成为亟待解决的问题。

目前常用的中长期负荷预测算法中，偏最小二乘回归预测模型对影响因子的利用比较有效，国内外相关研究也较多。文献[1]对最小二乘法做了一定改进后运用于中长期负荷预测中，取得了一定效果。但是利用偏最小二乘法进行中长期负荷预测，由于历史样本跨越时间较长，在建模过程中往往会带入过于久远的数据信息，会较大地影响回归模型在预测年的适用性。并且在主成份分析时，过多的影响因子会使主成份的构成变得复杂，从而使各主成份的实际含义解释变得模糊，最终影响整个模型的解释能力。

本文将粗糙集理论及D-S证据理论引入偏最小二乘法回归分析对负荷预测的计算中。首先本算法对中长期负荷预测中各影响因子的重要性即与负荷的相关程度进行排序，并利用K-means聚类分析法得出多组影响因子聚集；将历史年的各影响因子状况作为其属性，以历史年为对象进行聚类，得出多组历史年聚集。再分别利用偏最小二乘回归分析法对各组历史年的各组影响因子聚集进行建模，每一组历史年聚集可得出多个不同影响因子的多元回归分析模型。利用方差协方差权重优化算法，对相同年组内的不同预测模型进行权重值优化分配。最后采用基于D-S证据理论的信息融合算法对全部预测模型的权重方案进行融合，得出最终的组合预测模型。该建模过程充分利用了各影响因素及其对预测的关联性，考虑了建模中历史数据的广度及相似性，加强了多元回归模型的数学关系在预测年的适用性。最终目的是使建立的模型能考虑所有影响因子及历史年数据，同时能强化其中最优的数据组合，提高预测精度。经过算例验证，该方法有效提高了负荷预测的精确性。

1 基本理论

1.1 粗糙集理论

粗糙集方法是一种有效的软计算方法，不需要预先给定相关属性的数量描述，并能够直接从数据中提取出简洁且有效的决策规则，这为解决多因素综合电力负荷预测存在的冗余信息和噪音数据等问题提供了一条途径[2-4]。本文将粗糙集应用于电力负荷预测中，分析负荷(决策属性)对各影响因素(条件属性)的依赖度及各条件属性在条件属性集中的重要性。

粗糙集属性约简的具体步骤为

(1) 数据预处理和特征化数据。采用一定的粗糙集离散化算法将决策表中的条件属性和决策属性变量历史数据进行离散化。对离散化后的新决策表进行属性约简并得到约简后的决策规则。

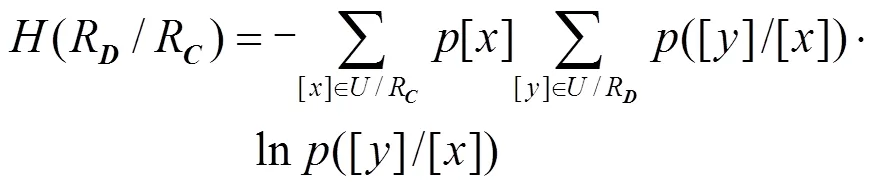
(3) 计算属性的权系数，并进行属性集的各因素的重要性排序。用式(2)、式(3)计算属性在属性集中的重要性。

(3)

1.2 D-S证据理论

1.2.1 D-S证据理论基础

D-S证据理论[5-6]是对贝叶斯统计推断理论的一种推广。D-S证据理论用“识别框架”表示所感兴趣的命题集，若识别框架在集函数(其中为的幂集)上满足：

1.2.2 基于证据理论的权重融合

(1) 方差协方差权重分配方法

本文选用方差协方差权重优化方法进行组合预测模型中各单一预测模型的权重分配[7]。假设有种预测模型，进行了期预测，则第种模型的第期预测值为，预测误差为，预测误差方差为，预测模型构成的组合预测结果为

(6)

(8)

(2) 证据理论Dempster合成法则

在权重进行融合时，对预测精度较高的预测值赋予较大的权重，对预测精度较低的预测值赋予较小的权重，这与证据理论中基本可信度分配满足的条件类似，因此可以通过类比的思想，利用证据理论的Dempster合成法则对多组权重进行融合，在负荷预测融合模型中，模型权重就类似于证据理论的基本信度值。利用式(10)信度的合成法则进行融合，融合后的基本信度值可作为预测模型融合的权重。

2 基于粗糙集方法和D-S证据理论的多元回归组合负荷预测方法

电力系统负荷预测的过程通常包括许多不确定因素，如原始数据观测误差、特征属性选择、预测算法选择等。针对单因素不确定性的分析和处理方法有很多种，但电力系统是受多种因素影响的复杂非线性系统，负荷预测过程复杂，只有同时减少多种因素带来的不确定性才能达到较好的预测效果。为减少负荷预测属性选择的影响，可采用粗糙集方法计算各属性的影响程度并排序[8-11]，用K-means聚类算法对历史年和排序后的影响因子进行分组，然后对各组统一采用偏最小二乘回归分析方法进行预测得到各组的预测结果，再利用D-S证据理论融合为一个最终的预测结果[12-15]。

基于粗糙集理论和D-S证据理论的多元回归组合预测方法如图1所示的6个步骤。

图1 负荷预测算法流程图

步骤1：利用粗糙集算法对影响因子进行分析，得出各影响因子对电量的影响程度，并利用K-means算法，对影响因子进行聚类分析，再根据建模需求简化得出组影响因子。

步骤2：以影响因子为对象属性，对历史年进行K-means聚类，再根据建模需求进行简化，得到组历史年。

步骤3：依次利用组历史年中的组影响因子进行多元回归建模，可得到个模型，如式(11)所示。

步骤5：利用D-S证据理论将组权重进行融合，得到最终权重分配方案。1个组合预测模型中有个多元回归模型，分别对应了组影响因子聚集。

步骤6：利用与预测年为同一聚集的历史年数据建立组合预测模型，并进行负荷预测。

3 算例分析

采用XX地区1999~2013年社会经济及全社会电量数据，如表1，对该地区2014年的用电量进行预测。

步骤1：利用1999至2013年的历史值，计算出各影响因子在条件属性集中对决策属性全社会用电量的重要程度，其结果如表2所示。以影响因子的重要程度为对象属性对影响因子进行聚类分析，其结果如下：

上述5组简化为3组可得

根据建模的需要变化为

经过简化后的分组既保持了原本的重要性分级，也简化了后面的建模数量。

步骤2：以1999至2014年为对象，以影响因子为属性对历史年进行聚类，其结果如下：

将以上5组简化为3组可得

步骤3：由于2014年为预测年，因此不将其用于建模，利用以上分组依次建立回归模型如下：

表1 XX地区1999~2014年社会经济指标及全社会用电量

表2 条件属性集合中各条件属性的重要程度

步骤4：对各组中的三个预测模型进行组合权重分配，其结果如表3所示。

表3 各组预测模型对应权重

步骤5：利用D-S证据理论关于基本可信度分配概念，结合前述的数学模型，将表3中的权重转化为相应的基本信度值，再通过信度函数的Dempster合成法则将对应的信度函数进行多重融合，即可得到预测年各组的预测模型权重。权重的具体融合结果如表4所示。

表4 权重的具体融合结果

步骤6：根据上述历史年的聚类结果可知，2014与2008~2013的发展情况最为相似，因此选用2008~ 2013年的数据建立回归模型，即。

选用表4中二重融合权重值为组合预测模型中三个预测模型的权重，则最终的预测模型为

最终预测结果如表5所示。

表5 2014年年电量预测结果分析

由表5中五种预测模型的结果分析可知：

②方差-协方差组合预测模型准确率比任意单一预测模型准确率都高。说明组合预测模型比单一预测模型预测效果更好。

③粗糙集D-S模型的准确率较方差-协方差组合预测模型有一定提高，对单一预测模型有较大提高，说明其权重分配方法效果更好，能有效提高预测结果。

4 结语

本文提出了基于粗糙集方法和D-S证据理论改进的多元回归中长期负荷预测方法。本算法利用粗糙集理论对影响因子进行重要性排序，并以重要性为其属性进行聚类。之后对历史年进行聚类，并以不同的影响因子组与历史年组进行搭配建立多个多元回归模型，利用相同年组的多个回归模型建立组合预测模型，得到多组权重值。最后利用D-S证据理论对多组权重值进行融合，得出最终权重分配方案。此方法即保留了全部历史资料信息，又优化了各影响因子及历史年对模型建立的影响程度，使多元回归建模过程中对历史资料的运用更加合理。由算例结果分析可知，基于粗糙集理论和D-S证据理论改进的多元回归算法相对于单一多元回归预测模型在预测精度上有较大的提高，有较好的实用性。

[1] 季泽宇, 袁越, 邹文仲. 改进偏最小二乘回归在电力负荷预测中的应用[J]. 电力需求侧管理, 2011, 13(1): 10-14.

JI Zeyu, YUAN Yue, ZOU Wenzhong. Application of improved partial least square regressive model in power load forecasting[J]. Power Demand Side Management, 2011, 13(1): 10-14.

[2] 尹东阳, 盛义发, 蒋明洁, 等. 基于粗糙集理论-主成分分析的Elman神经网络短期风速预测[J]. 电力系统保护与控制, 2014, 42(11): 46-51.

YIN Dongyang, SHENG Yifa, JIANG Mingjie, et al. Short-term wind speed forecasting using Elman neural network based on rough set theory and principal components analysis[J]. Power System Protection and Control, 2014, 42(11): 46-51.

[3] WANG Guoyin, HE Li. Rough set extensions in incomplete information systems[J]. Frontiers of Electrical and Electronic Engineering in China, 2008, 35(4): 68-79.

[4] 肖河, 肖盛.基于粗糙集理论的遗传神经网络风速预测模型[J]. 电网与清洁能源, 2012, 28(9): 82-87.

XIAO He, XIAO Sheng. Wind speed forecasting model of genetic algorithm neural network based on rough set theory[J]. Power System and Clean Energy, 2012, 28(9): 82-87.

[5] 朱建全, 刘锋, 梅生伟, 等.基于证据推理的电力负荷建模[J]. 电工技术学报, 2015, 30(15): 89-95.

ZHU Jianquan, LIU Feng, MEI Shengwei, et al. Electric load modeling based on evidence reasoning[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 89-95.

[6] 李玲玲, 刘敬杰, 凌跃胜, 等.物元理论和证据理论相结合的电能质量综合评估[J]. 电工技术学报, 2015, 30(12): 383-391.

LI Lingling, LIU Jingjie, LING Yuesheng, et al. Power quality comprehensive evaluation based on matter-element theory and evidence theorys[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 383-391.

[7] 贺辉. 电力负荷预测和负荷管理[M]. 北京: 中国电力出版社, 2013.

[8] 张庆宝, 程浩忠, 刘青山, 等. 基于粗糙集属性约简算法和支持向量机的短期负荷预测[J]. 电网技术, 2006, 30(8): 56-59, 70.

ZHANG Qingbao, CHENG Haozhong, LIU Qingshan, et al. Short-term load forecasting based on attribute reduction algorithm of rough sets and support vector machine[J]. Power System Technology, 2006, 30(8): 56-59, 70.

[9] 李伟, 闫宁, 张振刚. 基于粗糙集的混合支持向量机长期电力负荷预测研究[J]. 电力系统保护与控制, 2010, 38(13): 31-34.

LI Wei, YAN Ning, ZHANG Zhengang. Study on long-term load forecasting of MIX-SVM based on rough set theory[J].Power System Protection and Control, 2010, 38(13): 31-34.

[10] 李永德, 李红伟, 张炳成, 等. 融合粗糙集与神经网络的燃气轮发电机组振动故障诊断方法[J]. 电力系统保护与控制, 2014, 42(8): 90-94.

LI Yongde, LI Hongwei, ZHANG Bingcheng, et al. Fault diagnosis of gas turbine generator set by combination of rough sets and neural network[J]. Power System Protection and Control, 2014, 42(8): 90-94.

[11] 蒋亚坤, 李文云, 赵莹, 等. 粗糙集与证据理论结合的电网运行优质性综合评价[J]. 电力系统保护与控制, 2015, 43(13): 1-7.

JIANG Yakun, LI Wenyun, ZHAO Ying, et al. Evaluation of power quality performance based on rough set and evidence theory[J]. Power System Protection and Control, 2015, 43(13): 1-7.

[12] 吴京秋, 孙奇, 杨伟, 等. 基于D-S证据理论的短期负荷预测模型融合[J]. 电力自动化设备, 2009, 29(4): 66-70.

WU Jingqiu, SUN Qi, YANG Wei, et al. Short-term load forecasting model fusion based on D-S evidence theory[J]. Electric Power Automation Equipment, 2009, 29(4): 66-70.

[13] 李玲玲, 曹丽鹏, 刘伯颖, 等. 多属性系统中的属性权重分配方法[J]. 电工技术学报, 2015, 30(1): 422-527.

LI Lingling, CAO Lipeng, LIU Boying, et al. The method of attribute weight distribution in multi-attribute system[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 422-527.

[14] 齐振忠. 多信息融合的变压器实时状态评估[J]. 高压电器, 2012, 48(1): 95-99.

QI Zhenzhong. Real-time status evaluation of transformer with multi-information fusion technology[J]. High Voltage Apparatus, 2012, 48(1): 95-99.

[15] 赵云峰, 张永强, 聂德鑫, 等.基于模糊和证据理论的变压器本体绝缘状态评估方法[J]. 电力系统保护与控制, 2014, 42(23): 57-62.

ZHAO Yunfeng, ZHANG Yongqiang, NIE Dexin, et al. Application of fuzzy and evidence theory in power transformers condition assessment[J]. Power System Protection and Control, 2014, 42(23): 57-62.

(编辑 魏小丽)

Improved multiple regression load forecasting method based on rough set theory and D-S evidence theory

CHEN Yibo1, ZHENG Ling2, YAO Jiangang2

(1. State Grid Information & Communication Company of Hunan Province, Changsha 410007, China;2. College of Electrical and Information Engineering, Hunan University, Changsha 410012, China)

Nowadays, multivariate regression algorithm is mostly adopted in the mid-long term load forecasting, but it lacks good theoretical foundation for the selecting of the impact factors and the past years when modeling. It is difficult to make a balance between considering more affecting factors, historical data and reducing the regression model error, which leads to the inaccuracy of the multivariate regression algorithm in actual load forecasting. Rough set theory and D-S evidence theory are applied to the multivariate regression algorithm. First, rough set theory is used to sort the importance of influencing factors, and then the impact factors and the historical years are clustered respectively, so that several multiple regression models can be built. Additionally, the weights of different models are fused by using D-S evidence theory. In this way, the final combination forecasting model based on the multivariate regression analysis method can be built. According to the valid example, it can be concluded that the final model can preferably balance the selection of impact factors and past years while effectively improve the accuracy of the multiple regression algorithm in the mid-long term load forecasting, which provides stronger applicability at the same time.

mid-long term load forecasting; multivariate regression algorithm; rough set theory; D-S evidence theory

10.7667/PSPC150852

2015-05-20；

2015-07-14

陈毅波(1982-)，男，博士，工程师，主要从事面向电力信息基础平台的信息关键技术研究；E-mail: chenyibo8224@gmail.com 郑 玲(1991-)，女，通信作者，硕士研究生，研究方向为电力系统负荷预测；E-mail: 15116403583@163.com 姚建刚(1952-)，男，教授，博士生导师，主要从事高电压绝缘技术、电力系统自动化和电力市场理论及其应用方面的研究。E-mail: yaojiangang@126.com