基于ACA-PID算法的风机独立变桨控制

周腊吾，邓宁峰，陈 浩，韩 兵，田 猛



基于ACA-PID算法的风机独立变桨控制

周腊吾1，邓宁峰1，陈 浩2，韩 兵1，田 猛1

(1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.湖南世优电气股份有限公司，湖南 湘潭411100)

为了缓解大型风机在额定风速以上出现的不平衡载荷问题，针对变速变桨风电机组，给出了一种基于蚁群算法优化PID参数的风机独立变桨控制策略。利用蚁群算法的寻优特性，优化传统PID变桨控制器的参数，使其兼有PID控制的精简性与蚁群算法的自适应性，给出了其具体的实施步骤。构建了风力发电机独立变桨控制模型，对新策略与传统策略进行了仿真与实验。仿真与实验结果表明，基于蚁群算法优化PID参数的风机独立变桨控制策略是有效和实用的，该策略能提高控制系统的动态性能，有效地减少不平衡载荷，改善风机的振动状态。

风电机组；独立变桨控制；蚁群算法；PID；不平衡载荷

0 引言

随着常规能源的弊端显现，可再生能源越来越受到人类的重视，风电由于其技术成熟、灵活性强的优点，成为发展最快的可再生能源之一[1-4]。近年以来风力发电机朝着大型化的方向发展，叶轮的直径不断增大，叶轮上不平衡载荷引起的风力机疲劳失效成为风电运行维护成本的主要来源[5-6]。传统的统一变桨控制的桨距角给定是由风速、风机转速、输出功率的反馈来确定的，其在功率控制的同时，无法兼顾叶轮的不平衡载荷，由此衍生出了独立变桨控制方法，它通过分别对风机桨叶进行单独微调，在保证发电机输出额定功率的情况下，减小了因风速的湍流特性、风剪切和塔影效应所造成的风机不平衡载荷[7]。

近年来，国内外对统一距与独立变桨的策略和方法有着大量的研究，都具有各自的特点。文献[8]深入研究了模糊控制器在风机中的应用，将输出功率作为反馈信号，以桨距角信号作为控制输出，设计了基于模糊控制的桨距角控制器。文献[9]将神经网络算法应用进入风力发电机组的控制当中，利用神经网络的自适应性、学习能力调节桨距角，使得风机的动态性能得到提升，但是系统存在稳态误差。文献[10]提出基于前馈补偿的方位角权系数分程独立变桨控制，此控制方法采用方位角权系数分配分别对3个桨叶的桨距角进行调整，实现独立变桨控制，然后根据前馈补偿理论对距过程进行分程独立变桨控制。文献[11]采用多变量LQG控制策略为解决独立变桨控制多输入多输出信号之间的耦合问题，LQG控制器是基于风机控制系统的数学模型进行设计的，该数学模型通常有一些约束条件，与实际风机的动态特性差别大。

PID控制器有着简单、精确的优点，但也有动态性能较差的缺点。本文提出了基于蚁群算法PID参数优化的风机独立变桨控制策略，利用蚁群算法的全局寻优能力，优化变桨PID控制器的参数，给出蚁群算法对PID参数优化的方法与具体实施步骤，并且进行了仿真与半实物平台研究，最后结果验证了基于蚁群算法PID参数优化的风机独立变桨控制策略具有较好的控制效果，可以有效减少不平衡载荷，改善风机的振动状态。

1 风力机特性与独立变桨控制

风机将风能转化为电功率，其输出功率可由式(1)表示。

式中：a为空气密度；为风轮半径；为风速；为桨距角；为叶尖速比(=/，为风轮角速度)；p为风能利用系数。

风能利用系数p由风机叶片的空气动力学特性确定，其可以通过叶尖速比与桨距角的多项式近似拟合[12]，如图1所示。

图1 不同桨距角下风力机Cp-l特性曲线

由图1可知，随着的增大，对应p-特性曲线的p极大值逐渐减小；1=0º时，存在一个最佳叶尖速比opt使风能利用系数达到最大pmax；此最佳叶尖速比opt所对应的最佳风轮角速度opt为

最佳叶尖速比opt由风轮的自身参数所决定，可知在不同的风速下，总存在一个使得风能利用系数达到最大，从而获得最佳输出功率。图2为各风速下风机的-功率特性曲线，曲线abcde即风机的运行曲线。

图2 各风速下风力机-功率特性曲线

Fig. 2 Wind turbine generator’s power curve - at different wind speed

当风速小于切入风速1时，风机处于最小转速min下，并未开始发电，即ab段；当风速在1和5之间时，随着风速的增大，风轮转速始终跟随最佳风轮角速度opt逐渐增加，p随之增大，风机进入变速运行区bc段，此段情况下，独立变桨控制主要是为了维持p保持最佳；当运行至c点时，风速为4，风轮转速达到额定转速ω时，此时风机进入恒速运行区，由于风轮捕获的能量也在增加，输出功率进一步增大；当运行至d点时，风速为额定风速5时，输出功率达到额定值n，风速继续增大，为保持输出功率的恒定，统一变桨控制通过增大风轮叶片桨距角来限制风轮捕获的能量，直至风速达到切出风速6风机顺桨停机，即图2中de段。

风机运行于de段时，由于处于高风速段，风速的湍流特性、风剪切和塔影效应对风机的影响增大，加剧了不平衡载荷现象，从而导致了功率波动和机械部件的疲劳损耗，此段情况下，独立变桨控制即为了减弱这种风轮所受的不平衡载荷。风机所受的叶根弯矩是一个周期时变量，不利于计算与控制系统的设计，本文使用Coleman坐标变换[13]。如图3所示，将位于叶片根部的压力传感器所测得的叶根拍打力矩x、y、z与叶片方位角转换为d、q坐标轴上的俯仰弯矩d与偏航方向弯矩q，然后通过蚁群算法优化PID参数控制器得到d和q，d与q经反变换得到独立变桨控制信号x、y、z，此信号与统一变桨控制器信号0相加即得到变桨控制信号1、2、3。

图3 独立变桨控制框图

2 ACA-PID独立变桨控制器

2.1 ACA-PID控制器的基本原理

目前来说，PID控制器以其结构简单、控制精确等特点被广泛应用于风力发电机组的变桨控制中，但是风机有着较强的转动惯量、非线性耦合和风速变化的随机性，以致PID控制算法不能很好的抑制风机的动态载荷[14]。运用现代智能控制算法与PID控制策略相结合，构成复合型与智能型的PID控制策略，具备自适应性、自学能力，能够优化、自整定控制参数，并且也具有PID控制器结构简单、稳定性强、控制精确的特点。

蚁群算法(Ant Colony Algorithm，ACA)是一种仿生型的具有正反馈和分布式协作特征的算法，其通过信息素的积累和更新寻找最优路径[15]，本文使用蚁群算法来动态调整PID控制器参数[16]，基于蚁群算法的PID控制器基本结构如图4所示。

图4 蚁群算法PID控制结构图

图中：()为输入量(对应d、q轴弯矩)；()为输出量(对应独立变桨控制信号d、q)；控制对象为不平衡载荷；()为控制量，()为偏差量。

在控制对象模型与取样周期已知的情形下，PID控制器只有3个参数p、I、D需要确定。类比于旅行商问题，每只蚂蚁的寻优过程可由一个二维坐标系来表示。如图5所示，蚂蚁所经过节点连成的路径代表其所寻的PID参数，其中横坐标中0为起点或终点，1~5代表p，6~10代表I，11~15代表D，纵坐标值代表各参数的某一位，具体来讲，从小到大依次为参数的个位和小数点后的4位。图5中p=6.2756，I=4.8351，D=6.8953。

图5 每只蚂蚁的寻优过程

通常我们需要一个性能指标来评价控制系统的性能，本文考虑了误差、上升时间、超调量等约束条件，采用如下的性能指标(目标函数)

式中：u为上升时间；()=()-(-1)；1、2、3、4为权值且42；为仿真计算的总点数。

对于参与PID参数优化的蚁群算法来说，其所搜索出的最佳路径就代表了最优性能指标，并且不同于旅行商问题，PID参数优化的蚁群算法是根据目标函数值来更新信息素物质的浓度，而不是路径长度。定义蚂蚁从节点到节点的转移概率为

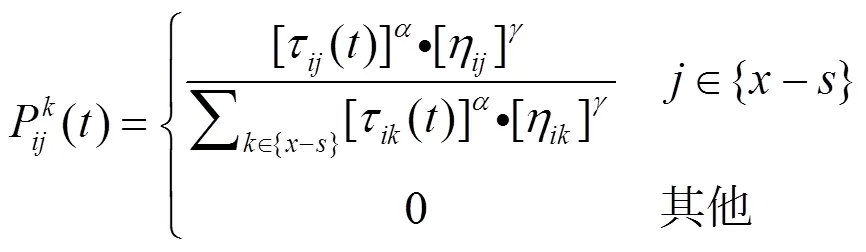
式中：为节点总数；为第个节点；为信息素浓度；为可访问度；和为控制信息素和能见度之间相对重要性的参数，影响算法的收敛速度和收敛性[17]。算法每迭代次，信息素浓度将根据下面的公式进行更新

(5)

式中：为信息素挥发系数；为蚂蚁总数；D为第只蚂蚁在时刻与+时刻之间留在支路(,)上的单位长度的信息素浓度，可按下式计算

(7)

式中：为蚂蚁释放的信息素浓度；s为蚂蚁的路径，k表示蚂蚁所搜寻的目标函数的值。

可访问度定义为前后2次周游所确定的目标函数值的差，如式(8)所示。

2.2 自适应调整信息素挥发系数

对于最基本的蚁群算法，其在迭代过程中常常会陷入局部最优或者停陷，使得搜索时间变长。国内外学者提出了多种改良措施，本文借鉴采取了一种自适应调整信息素挥发系数的方法用以改良基本蚁群算法，如式(9)所示。

式中：为信息素挥发系数；为迭代次数。

在迭代初期值较大，即可增强蚁群算法寻找新解的能力，在迭代后期挥发系数值较小，以便搜索更为集中。

2.3 算法的收敛性分析

关于蚁群算法的马尔科夫链描述，定义一个随机过程，如式(10)所示。

式中：()为图5中蚂蚁路径上迭代次后的信息素浓度；^()表示迭代次后的最优路径；()为此时的目标函数值。

每只蚂蚁的解()的求结过程由(4)式所决定，而^()与()是由()所决定的，()、^()和(-1)通过式(10)共同确定()，这表明随机过程()由当前状态与下一状态决定，状态转移概率取决于，所以()为非时齐有限状态马尔科夫链[18]。

假设蚂蚁一直未通过节点(,)，在这种状况下，信息素在迭代次后最小，此时有

令

(12)

且

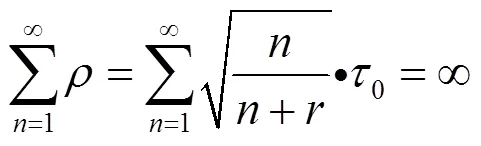
则马尔科夫链中当→∞时，其以概率1逼近最优状态。*为最优路径，当节点(,)∈*时，[*]=max，否则为0。对于本文的二维节点来说，迭代时间往往很短，不超过100就能达到很好的效果(满足目标函数)。

2.4 算法实施的具体步骤

蚁群算法PID参数优化的步骤如图6所示。

图6 蚁群算法PID参数寻优基本流程

3 仿真研究

本文使用FAST软件与Matlab联合对基于蚁群算法的独立变桨控制系统进行仿真，采用5 MW三桨叶风力发电机组，其具体参数如表1所示。

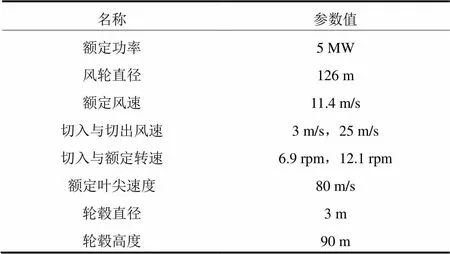
表1 风力发电机组参数表

ACA-PID算法参数设置：=20，=1，=1，0=0.7，=100，=100；仿真采用的随机风速信号风速在10~17 m/s之间，为额定风速以上区间，图7为桨叶1上的水平风速。

对统一变桨(CPC)和独立变桨(IPC)分别进行仿真，桨距角给定调节变化曲线如图8所示。

桨1的叶根偏航(面内)弯矩、俯仰(面外)弯矩对比如图9、图10所示。

图7 桨叶1上的水平风速

图9 桨1叶根偏航(面内)弯矩

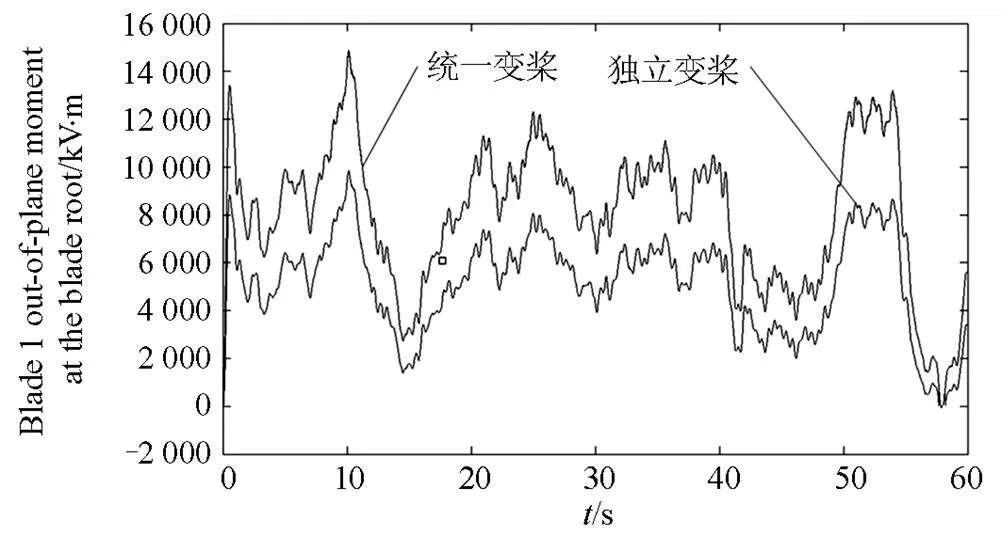
图10 桨1叶根俯仰(面外)弯矩

CPC与IPC的弯矩变化如表2所示。

表2 统一变桨(CPC)与独立变桨(IPC)的叶根弯矩变化

从图9、图10可以看出，独立变桨(IPC)下叶根弯矩的大小、振幅已明显减小。由表2可知，独立变桨(IPC)下叶根偏航弯矩的平均值下降约34.2%，叶根俯仰弯矩的平均值下降约36.5%，并且叶根偏航、俯仰弯矩的标准差也分别下降约30.0%和30.9%，这进一步表明叶根弯矩的大小、振幅明显减小。这些数据验证了ACA-PID独立变桨控制对于减小风机的不平衡载荷有较好的效果，能够很好的抑制由偏航、俯仰弯矩所造成的风机传动机构的振动，从而稳定输出功率，改善风机疲劳程度。

4 实验分析

如图11所示，本文对此测试平台进行了独立变桨实验研究，该平台由独立变桨控制柜、变桨电机对拖测试系统、上位机等组成。

图11 独立变桨测试平台

本节首先测试了ACA-PID独立变桨控制器的对于斜坡信号跟踪性能(模拟风速平稳变化)，给予驱动器命令模拟轮毂上的水平风速，信号给定如图12所示，其风速值在11 m/s与17 m/s之间。

图12 轮毂水平风速(斜坡信号)

从图13中可清楚的了解到，ACA-PID控制方式与传统PID控制方式，斜坡信号响应几乎一致且很稳定，这表明ACA-PID控制方式能够及时搜寻到最优参数，具有与传统PID控制方式相差无几的稳定性，能够准确无误的跟踪平稳风速变化。

随后本节测试了两种控制方式对于方波风速信号的响应(模拟风速剧烈变化)，其风速值在13m/s与17m/s之间，如图14所示。

图14 轮毂水平风速(方波信号)

从图15可知，ACA-PID控制方式的超调量、调节时间约为5.62%、0.91 s，都远远小于传统PID控制的19.33%、1.60 s，且未出现震荡现象。这验证了蚁群算法能够很好的对PID参数进行动态寻优，克服传统PID控制方式参数一成不变的缺点，对于阵风有着更快、更稳定的响应。

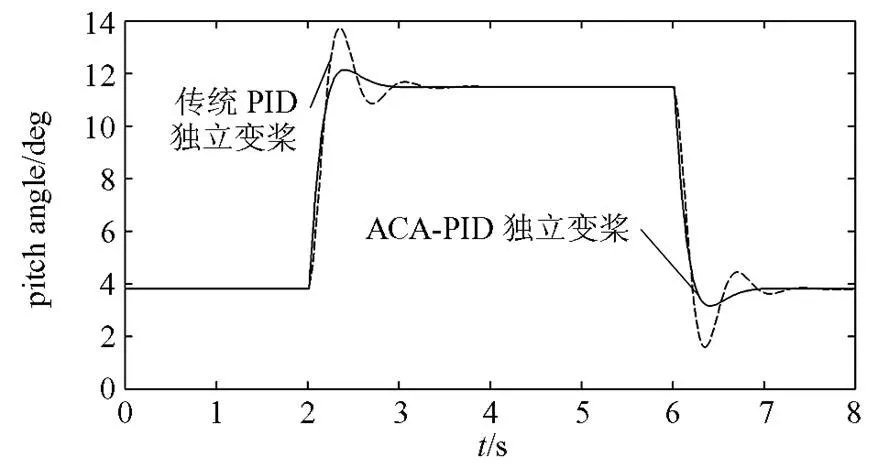
图15 桨距角响应(方波信号)

5 结束语

由于受湍流、风切变、塔影效应等影响，大型风机在额定风速以上区间时所受的不平衡载荷会导致风机运行的不稳定，独立变桨控制即是为减小载荷而提出的。另外，因为风机有着较强的转动惯量、非线性耦合和风速变化的随机性，以致PID控制算法不能很好的抑制风机的动态载荷。针对这种情况，本文提出了一种基于蚁群算法的PID参数优化独立变桨控制器，利用蚁群算法的正反馈和分布式协作来寻找PID控制器的最优参数。通过仿真与测试平台实验研究，验证了基于ACA-PID的独立变桨控制系统拥有较好的动态性能，对于抑制叶根弯矩有明显的效果，进而缓解风机的振动。

[1] 董永平, 何世恩, 刘峻, 等. 低碳电力视角下的风电消纳问题[J]. 电力系统保护与控制, 2014, 42(5): 12-16.

DONG Yongping, HE Shien, LIU Jun, et al. Wind power consumption issue in the view of low carbon power[J]. Power System Protection and Control, 2014, 42(5): 12-16.

[2] 张元, 郝丽丽, 戴嘉祺. 风电场等值建模研究综述[J]. 电力系统保护与控制, 2015, 43(6): 139-146.

ZHANG Yuan, HAO Lili, DAI Jiaqi. Overview of the equivalent model research for wind farms[J]. Power System Protection and Control, 2015, 43(6): 139-146.

[3] 艾斯卡尔, 朱永利, 刘少宇, 等. 基于永磁直驱风电机组的风电场电压控制问题分析[J]. 电器与能效管理技术, 2014(19): 55-59.

Aisikaer, ZHU Yongli, LIU Shaoyu, et al. Discussions on the control and management of reactive power/voltage of wind farm[J]. Electrical & Energy Management Technology, 2014(19): 55-59.

[4] 景天, 王西田, 沈嘉怡. 一种大规模风电集中直流外送方案[J]. 电器与能效管理技术, 2015(9): 50-54.

JING Tian, WANG Xitian, SHEN Jiayi. A scheme for large-scale wind power centralized DC transmission[J]. Electrical & Energy Management Technology, 2015(9): 50-54.

[5] RIBRANT J, BERTLING L. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997-2005[J]. IEEE Transactions on EnergyConversion, 2007, 22(1): 167-173.

[6] 窦真兰, 施刚, 曹云峰, 等. 减少风力机转矩波动的异步变桨控制[J]. 电工技术学报, 2014, 29(1): 236-245.

DOU Zhenlan, SHI Gang, CAO Yunfeng, et al. Individual pitch control for reducing wind turbine torque fluctuation[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 236-245.

[7] 崔双喜, 王维庆, 张强. 风力发电机组独立变桨鲁棒自适应桨距角跟踪控制[J]. 电力系统保护与控制, 2015, 43(6): 52-57.

CUI Shuangxi, WANG Weiqing, ZHANG Qiang. Robust adaptive blade pitch angle tracking control for wind turbines[J]. Power System Protection and Control, 2015, 43(6): 52-57.

[8] FARD M, RAHMANI R, MUSTAFA M W. Fuzzy logic based pitch angle controller for variable speed wind turbine[C] // Research and Development (SCOReD), 2011 IEEE Student Conference on. 2011: 36-39.

[9] MESEMANOLIS A, MADEMLIS C. A Neural Network based MPPT controller for variable speed wind energy conversion systems[C] // Distribution and Energy Conversion (MEDPOWER 2012), 8th Mediterranean Conference on, 2012: 1-6.

[10] 姚兴佳, 刘玥, 郭庆鼎. 基于前馈补偿方位角权系数的分程独立变桨控制研究[J]. 太阳能学报, 2012, 33(11): 532-539.

YAO Xingjia, LIU Yue, GUO Qingding. A control method for split range individual pitch based on feed- forward azimuth angle weight number assignment[J]. Acta Energiae Solaris Sinica, 2012, 33(11): 532-539.

[11] 邢作霞, 陈雷, 孙宏利, 等. 独立变桨控制策略研究[J].中国电机工程学报, 2011, 31(26): 131-138.

XING Zuoxia, CHEN Lei, SUN Hongli, et al. Strategies study of individual variable pitch control[J]. Proceedings of the CSEE, 2011, 31(26): 131-138.

[12] 王金铭, 卢奭瑄, 何新, 等. 大型风力发电机风能利用系数参数拟合的研究[J]. 太阳能学报, 2012, 33(2): 221-225.

WANG Jingming, LU Shixuan, HE Xin, et al. Study on parameters matching of rotor power coefficient for large scale wind turbine[J]. Acta Energiae Solaris Sinica, 2012, 33(2): 221-225.

[13] ZHANG Yunqian, CHEN Zhe, CHENG Ming. Proportional resonant individual pitch control for mitigation of wind turbines loads[J]. Renewable Power Generation, IET, 2013, 7(3): 191-200.

[14] 郭鹏. 模糊前馈与模糊PID结合的风力发电机组变桨控制[J]. 中国电机工程学报, 2010, 30(8): 123-128.

GUO Peng. Variable pitch control of wind turbine generator combined with fuzzy feed forward and fuzzy PID controller[J]. Proceedings of the CSEE, 2010, 30(8): 123-128.

[15] 张颖, 周韧, 钟凯. 改进蚁群算法在复杂配电网故障区段定位中的应用[J]. 电网技术, 2011, 35(1): 224-228.

ZHANG Ying, ZHOU Ren, ZHONG Kai. Application of improved ant colony algorithm in fault-section location of complex distribution network[D]. Power System Technology, 2011, 35(1): 224-228.

[16] NAVIDI N, BAVAFA M, HESAMI S. A new approach for designing of PID controller for a linear brushless dc motor with using ant colony search algorithm[C] // Power and Energy Engineering Conference. IEEE Conference Publications, 2009: 1-5.

[17] 周方, 张小凤, 张光斌, 等. 蚁群算法中参数设置对超声回波估计性能的影响[J]. 中国科学: 信息科学, 2013, 42(2): 243-253.

ZHOU Fang, ZHANG Xiaofeng, ZHANG Guangbin, et al. The effects of parameters settings of ant colony algorithm on the performance of ultrasonic echo estimation[J].Science China Information Sciences, 2013, 43(2): 243-253.

[18] 冯远静, 冯祖仁, 彭勤科. 一类自适应蚁群算法及其收敛性分析[J]. 控制理论及应用, 2005, 22(5): 243-253.

FENG Yuanjing, FENG Zuren, PENG Qinke. Adaptive ant colony optimization algorithms and its convergence[J].Control Theory & Applications, 2005, 22(5): 243-253.

(编辑 张爱琴)

Individual pitch control strategy based on ACA-PID controller in wind turbine

ZHOU Lawu1, DENG Ningfeng1, CHEN Hao2, HAN Bing1, TIAN Meng1

(1. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China; 2. Hunan Shiyou Electric Co., Ltd., Xiangtan 411100, China)

In order to alleviate the unbalanced load that occurred in operation above rated wind speed in large wind turbines, for variable speed variable pitch wind turbine, this paper gives IPC (independent pitch control) strategy based on PID controller which parameters can be optimized by ACA (Ant Colony Algorithm). It uses the optimization of ACA to optimize the parameters of traditional PID pitch controller, thus to makes it has adaptiveness of PID control and streamlining of ACA, and gives its specific implementation steps. The wind turbine IPC model is constructed and the simulation and experiment of the new strategy and the traditional strategy are made. The simulation and experimental results show that the IPC based on ACA-PID is effective and practical, it can enhance the dynamic performance of the control system, effectively reduce load imbalance and improve the vibrational state of the wind turbine.

wind turbine; individual pitch control; ant colony algorithm; PID; unbalanced load

10.7667/PSPC151482

国家国际科技合作专项(2011DFA62890)；湖南省研究生科研创新项目(CX2016B131)

2015-08-21；

2015-11-20

周腊吾(1965-)，男，博士，教授，主要研究方向为新能源发电技术、电力驱动与伺服理论及相关技术、新型电机电器设计及其控制；E-mail: 1021853001@qq.com邓宁峰(1992-)，男，通信作者，硕士研究生，研究方向为新能源发电技术。E-mail: 279579946@qq.com