PWM并网变换器多内模并联结构重复控制策略

卢闻州，周克亮，程 明，沈锦飞



PWM并网变换器多内模并联结构重复控制策略

卢闻州1，周克亮2，程 明3，沈锦飞1

(1.江南大学轻工过程先进控制教育部重点实验室，江苏 无锡 214122；2.英国格拉斯哥大学工学院， 格拉斯哥市 G12 8QQ；3.东南大学电气工程学院，江苏 南京 210096)

以“净化”电力系统中电力电子接口为背景，以实现并网电流快速、精确跟踪参考为目的，分析了多内模并联结构重复控制器(PSRC)及其控制系统。PSRC采用并联组成的一组+次谐波内模(=0, 1,…,-1)实现对所有谐波的零误差跟踪或扰动抑制。相对于常规重复控制器(CRC)，PSRC具有时间延迟小、收敛速度快、跟踪精度不下降、数字实现所需内存单元不增加的优点。将PSRC应用于恒压恒频(CVCF)脉宽调制(PWM)并网变流系统，包括三相/单相整流和三相/单相逆变并网系统中。实验结果验证了PSRC的有效性和优越性。

内模原理；重复控制；并联结构；脉宽调制(PWM)；并网变换器

0 引言

电力系统中的电网节点可以看成是一个具有二进制状态的电力接口，作为电力接口的电力电子变换器将发电/用电单元接入电网，电能在电力接口中作双向流动。电力电子变换器具有体积小、重量轻、效率高、成本低、响应快、噪音小、可模块化、功率密度大等诸多优点，在电力系统中将会扮演越来越重要的角色。但是变换装置本身也会带来一些诸如谐波污染的问题。因此，需要对电力电子接口进行“净化”，而“净化”的关键就是对电力电子变流系统进行精确控制，实现参考波形与实际波形的稳态零误差控制。

基于内模原理[1]的常规重复控制(CRC)[2]能够实现对周期性信号的稳态无差控制或扰动消除，只要事先已知这个信号的基波周期。在许多实际应用中[3-4]，需要跟踪或消除的周期性信号的谐波成分主要集中在一些特定的谐波频率处。研究者们已经在此角度对重复控制开展了一定程度的研究[3-11]。尤其文献[10-11]提出的多内模并联结构重复控制(PSRC)，就是一种通用的对全部谐波进行分类选择的重复控制器，用并联组成的一组+次谐波内模(=0, 1,,-1)来取代CRC的单一全谐波整体内模，实现对所有谐波的零误差跟踪或扰动抑制。在PWM三相整流器的应用中，采用CRC[12]已经能够获得比较良好的电流零误差跟踪特性及单位功率因数。但是与CRC相比，PSRC还具有时间延迟小、收敛速度快但数字存储单元不增加的优点。

因此，本文将PSRC应用于三相/单相PWM整流[13-15]和三相/单相PWM逆变并网系统[16-19]中，验证PSRC的有效性和优越性。

1 多内模并联结构重复控制器(PSRC)

1.1 PSRC

多内模并联结构重复控制器(PSRC)[10-11]如图1所示，传递函数如式(1)。

式中：k(=0, 1,,-1)是第+次谐波内模G() (=0, 1,,-1)的控制增益；为整数且≥0；由自然指数函数的性质[20]可得G()的传递函数为

(2)

或等效谐振之和形式：

从式(2)和式(3)中可以看到，第个单一模G()的极点位于基波频率的+倍频，即(±+)o，=0, 1, 2,,-1，=0, 1, 2,频率处，此时G()的模值趋近于无穷大，所以误差中的±+次谐波成分能够被完全跟踪或消除。因此，将个+次谐波内模(=0, 1, 2,,-1共个)并联组合，如图1所示，就可以具有对基波所有倍频谐波信号进行良好跟踪或消除的能力，并且可以“用户定制式”独立调节G()的增益k来改善PSRC的动态响应。

从式(3)还可以看到，±+次谐波频率项的系数为CRC的倍(参见文献[21]中式(3))，所以相同增益时PSRC单独针对±+次谐波的误差收敛速度比CRC快倍。因此，通过加权调节个G() (=0, 1, 2,,1)增益系数，可以优化PSRC总体误差收敛速率，获得比CRC更快的误差收敛速度。例如，奇次谐波为主时，令(1+3)>(0+2)能够在不降低跟踪精度的情况下提高总体误差收敛速率。

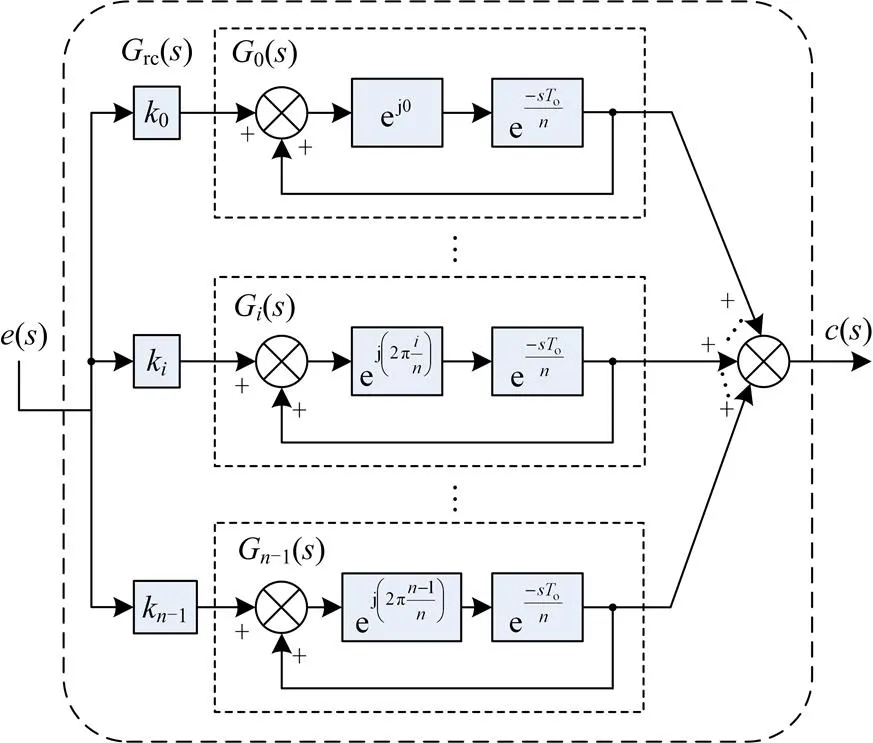
图1 多内模并联结构重复控制器(PSRC)

1.2 数字PSRC控制系统

实际应用中，重复控制器通常数字化，并加入低通滤波器()和相位补偿滤波器f()，保证系统的稳定性和鲁棒性[2]，得到改进型数字PSRC如下：

将重复控制器插入到传统的闭环反馈控制系统中，可以得到如图2所示插入式重复控制系统。其中：rc()是插入的重复控制器；c()是传统的反馈控制器；p()是控制对象；()是实际输出信号；ref()是参考输入信号；()=ref()-()是跟踪误差及rc()的输入；()是rc()的输出；()是c()的输出；()是外部扰动信号。

图2 插入式重复控制系统框图

插入PSRC后闭环反馈控制系统输出()为

(5)

式中：()为ref()到()的传递函数；d()为从()到()的传递函数；()为未插入重复控制器前的一般反馈控制系统的传递函数，如式(6)。

要使插入式的重复控制系统正常工作，需要在满足()系统稳定的前提下，满足插入式重复控制系统也稳定，即满足以下两个条件：

(1)()的极点(即1+c()p()=0的根)都在单位圆内；

(2)()和d()的极点(即1+rc()()=0的根)都在单位圆内。

由文献[10-11]，如果如图2所示的PSRC控制闭环系统是渐进稳定的，第(2)点稳定条件即控制增益k(=0,1,2,…,-1)满足以下不等式要求：

k≥0 (=0, 1, 2,,-1) (7)

因此，相同稳定范围内，PSRC能提供比CRC更快的误差收敛速度潜能。例如，奇次谐波为主时，只需增大对应的控制增益数值即可。

2 恒压恒频PWM并网变流系统

2.1 恒压恒频PWM并网变换器

如图3(a)、(b)所示是三相/单相PWM并网变换器的通用结构，都可工作在整流状态和并网逆变状态，分别对应三相/单相PWM整流器和三相/单相PWM并网逆变器。

若图3(a)工作于三相整流状态，则数学模型为

以及

(10)

式中：、和分别是电感、电容和电阻；L为电阻负载，L为反电动势；电感电流a、b、c和直流侧电容电压dc为状态变量；a、b、c为a、b、c三相的电网电压；dc为直流输出电流；L为直流负载电流；A、B、C为a、b、c三相的PWM调制电压。

图3 三相/单相PWM并网变换器通用结构

若图3(b)工作于单相整流状态，数学模型为

以及

(12)

式中：电感电流s和电容电压dc为状态变量；s为单相的电网电压；in为单相的PWM调制电压。

工作在三相/单相整流状态时，控制目标是：获得单位功率因数、较高电流跟踪精度和恒定输出直流电压。需对直流电压和交流电流进行控制，输出方程分别为式(13)和式(14)。

(14)

若图3(a)工作在三相并网逆变状态，则数学模型和式(9)完全一样，并假设dc恒定。

PWM调制电压可以描述为

直流输出电流可以写成：

(16)

式中，A、B、C为三相桥臂的开关函数，定义为

若图3(b)工作在单相并网逆变状态，则数学模型和式(11)完全一样，并假设dc恒定。

PWM调制电压可以描述为

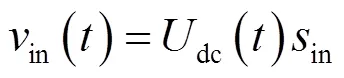
直流输出电流可以写成：

(19)

式中，in为单相桥臂的开关函数，定义为

工作在三相/单相并网逆变状态时，控制目标是：获得可调功率因数和较高电流跟踪精度。需对交流电流进行控制，输出方程分别为式(21)和式(22)。

(21)

2.2 控制系统

由式(9)，三相并网变换器可以解耦成三个完全独立的单相系统，因此无论三相还是单相，无论并网逆变还是整流控制系统的电流内环控制都可以是一样的，这里采用的DB+RC复合控制(具体见2.3节)同时适用于四种变换器模型。

如图4(a)所示三相PWM整流控制系统中，包含直流电压dc的外环PI控制，实现dc零误差跟踪给定，以及电感电流的内环，实现电感电流a、b和c较高精度跟踪参考。

如图4(b)所示单相PWM整流控制系统与图4(a)的主要区别在于电流信号数量只有一个，即电感电流s。

如图4(c)所示三相PWM并网逆变控制系统中，参考电流信号的生成通过给定有功和无功参考值、利用瞬时功率理论计算[22]及后续变换得到。电流内环控制与图4(a)类同。

如图4(d)所示单相PWM并网逆变系统中，参考电流中的幅值信号可由下式计算得到：

式中，s为电压s的有效值。而角度信号包含：电压锁相产生电压角度信号、PQ控制产生电压和电流间相位差角度信号以及电流参考方向和功率方向相反需进行角度反向调整的角度信号三部分。电流内环控制与图4(b)类同。

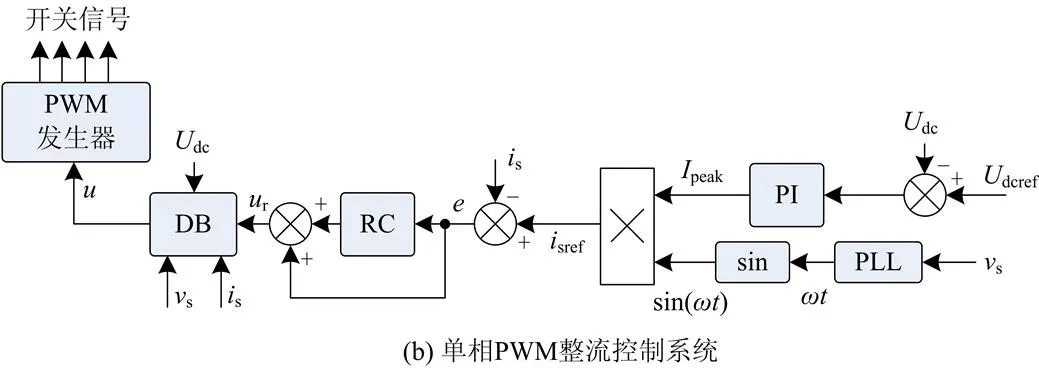
2.3 数字控制器的选取

采用的数字控制器为传统无差拍控制器(DB)和插入式重复控制器(RC)的复合控制器，其中插入式RC分为CRC和PSRC两种。

(a) DB

将三相并网变换器式(9)离散化后得

(24)

式中：a()、b()和c()为三相占空比；1=/，2=。

可将式(24)分解为三个独立的单相子系统：

式中，=a,b,c。

同理，单相并网变换器式(11)的离散形式为

式中，in()为占空比，1=/，2=。与三相离散式方程的差别只在直流电压相差一个1/2的系数。

为使控制器统一、简便，这里选择相同的DB控制器。于是DB控制器为

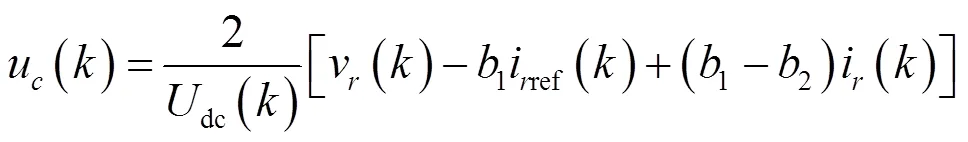
式中，三相时下标==a,b,c，单相时下标=in，=s，并且令iref()=i(+1)，=a,b,c，sref()=s(+1)。于是不带RC的闭环传递函数为()=-1，上述电流DB控制器是理论上只有一拍(即一个采样周期)控制延迟的无差拍控制器，从而能够提供快速的响应速度。

b. 插入式CRC

插入式数字CRC如下所示：

c. 插入式PSRC

插入式数字PSRC如下所示：

应用到三相并网变换器时，取=6，得到针对三相并网变流系统的PSRC(记为PSRC-6)如下：

(30)

应用到单相并网变换器时，取=4，得到针对单相并网变流系统的PSRC(记为PSRC-4)如下：

当然单相时也可以取=2，得到双模重复控制器[3-4](DMRC，本文记为PSRC-2)如下：

(32)

3 实验结果

3.1 整体平台及电路参数

为了验证PSRC在三相/单相并网变流系统中的有效性和优越性，搭建基于dSAPCE1104的三相/单相恒压恒频PWM IGBT变流系统实验平台，系统参数如表1和表2所示。

表1 三相/单相整流系统参数

表2 三相/单相并网逆变系统参数

将表1和表2参数代入式(27)，可得DB都为

对于三相/单相PWM整流和并网逆变系统，插入式CRC和PSRC的相位补偿滤波器都取实验中实际调试出来的最优值f()=3，来补偿系统中包括电流电压间相位延迟在内的各种时间延迟；选择CRC、PSRC-6、 PSRC-4和PSRC-2的滤波器分别为()=0.25+0.5+0.25-1，Q()=0.1+0.8+0.1-1(=0,1,2,3,4,5)，Q()=0.1+0.8+0.1-1(=0,1,2,3)和Q()= 0.20+0.6+0.20-1(=0,1)。选择PSRC-4的增益为0=2=0.1×rc,1=3=0.4×rc；选择PSRC-2的增益为0=0.2×rc,1=0.8×rc。为了具有可比性，选择各种RC增益相同，对CRC选择：rc=0.2，对PSRC-6满足：0+1+2+3+4+5=rc=0.2；对PSRC-4满足：0+1+2+3=rc=0.2；对PSRC-2满足：0+1=rc=0.2。

3.2 三相/单相PWM整流系统

a. 单独DB控制

图5(a)和图6(a)分别显示了三相和单相整流时单独DB控制的实验结果。两图中都可以看到：直流电压dc能够达到给定的参考电压120 V。但由于实验中多个环节的延迟作用，图5(a)中电感电流a对相电压a仍然有2~3拍时间延迟，而图6(a)中电感电流s对电压s仍然有约2拍的时间延迟，并且s过零点附近畸变比较明显。因此，本文加入CRC和PSRC，来提高三相/单相PWM整流系统的电流跟踪控制精度和获得单位功率因数，并进行比较研究。

b. DB+RC控制

图5(b)~(c)和图7显示了插入CRC和PSRC-6的三相整流系统稳态响应，图6(b)~(d)和图8显示了插入CRC、PSRC-4和PSRC-2的单相整流系统稳态响应，其中图5(b)~(c)和图6(b)~(d)显示了稳态电网(线)电压和电感电流波形，图7和图8分别显示了电感电流a和s的跟踪误差收敛变化波形。

从图5和图6都可以看出，CRC、PSRC-6、PSRC-4和PSRC-2都能使电流和电压间的相位差得到补偿，克服了DB单独作用时的缺点，实现了单位功率因数。从图7和图8中都可以看到，PSRC-6、PSRC-4、PSRC-2和CRC一样，都能使电流的跟踪误差得到下降，实现电流的精确控制。从图7和图8中还可以看到，CRC和PSRC-6、PSRC-4、PSRC-2的电流误差跟踪收敛时间分别为：0.32 s和0.14 s、0.18 s、0.20 s，因此可得，相对CRC，PSRC-6、PSRC-4、PSRC-2都能使电流的误差收敛速率得到大幅提高，最快能够接近CRC的三倍(PSRC-6)和两倍(PSRC-4、PSRC-2)，实现电流的快速控制。而PSRC-6、PSRC-4、PSRC-2和CRC占用相同的数字存储单元。

因此，上述实验验证了PSRC在三相/单相PWM整流系统中的有效性和相对CRC的优越性。

图7 加入RC后三相整流系统电流误差收敛波形图

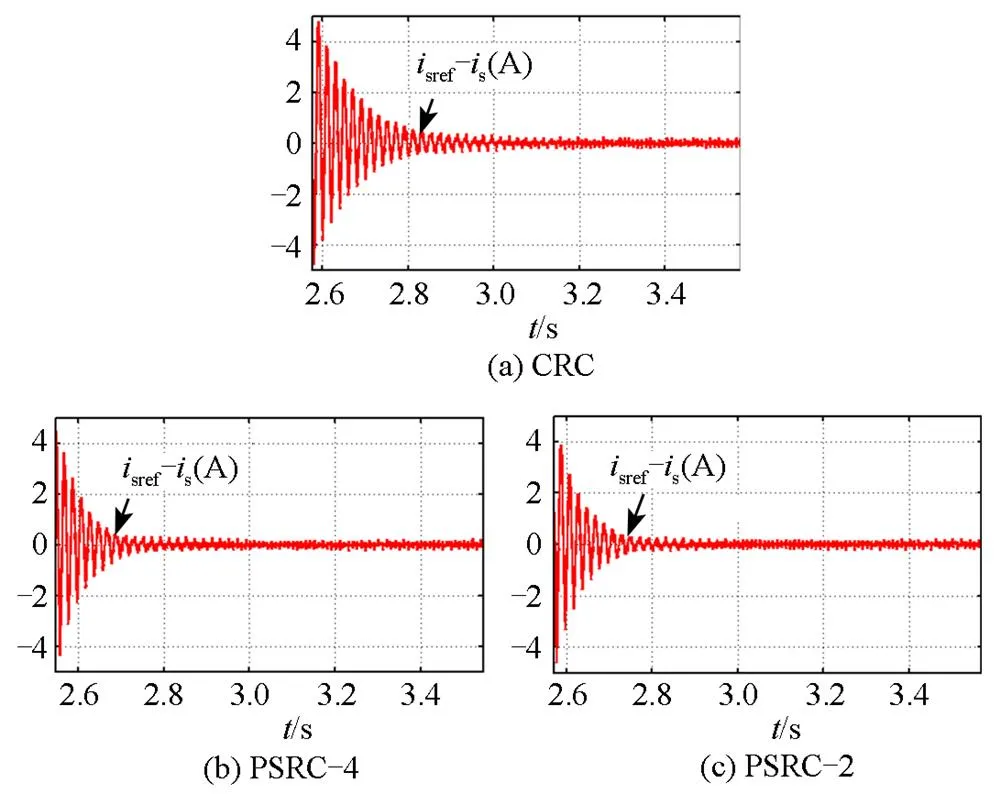
图8 加入RC后单相整流系统电流误差收敛波形图

3.3 三相/单相PWM并网逆变系统

a. 单独DB控制

图9(a)和图10(a)分别显示了三相和单相逆变并网时单独DB控制的实验结果。两图中都可以看到，电流畸变还是比较严重的，并没有形成一条比较光滑的正弦波。因此，本文加入CRC和PSRC，来提高三相/单相PWM逆变并网系统的电流跟踪控制精度，并进行比较研究。

b. DB+RC控制

图9(b)~(c)和图11显示了插入CRC和PSRC-6的三相逆变并网系统稳态响应，图10(b)~(d)和图12显示了插入CRC、PSRC-4和PSRC-2的单相逆变并网系统稳态响应，其中图9(b)~(c)和图10(b)~(d)显示了稳态电网(线)电压和电感电流波形，图11和图12分别显示了电感电流a和s的跟踪误差收敛变化波形。

从图9和图10中都可以看出，CRC、PSRC-6、PSRC-4和PSRC-2都能使电流的畸变得到明显改善。从图11和图12中都可以看到，PSRC-6、PSRC- 4、PSRC-2和CRC一样，都能使电流的跟踪误差得到下降，实现电流的精确控制。从图11和图12中还可以看到，CRC和PSRC-6、PSRC-4、PSRC-2的电流误差跟踪收敛时间分别为：0.32 s和0.14 s、0.20 s、0.20 s，因此可得，相对CRC，PSRC-6、PSRC-4、PSRC-2都能使电流的误差收敛速率得到大幅提高，最快能够接近CRC的三倍(PSRC-6)和两倍(PSRC-4、PSRC-2)，实现电流的快速控制。而PSRC-6、PSRC-4、PSRC-2和CRC占用相同的数字存储单元。

因此，上述实验验证了PSRC在三相/单相PWM并网逆变系统中的有效性和相对CRC的优越性。

图9 三相逆变并网系统稳态响应波形(x轴：2.5 ms/格，y轴：20 V/格和2 A/格)

图10 单相逆变并网系统稳态响应波形(x轴：2.5 ms/格，y轴：20 V/格和2 A/格)

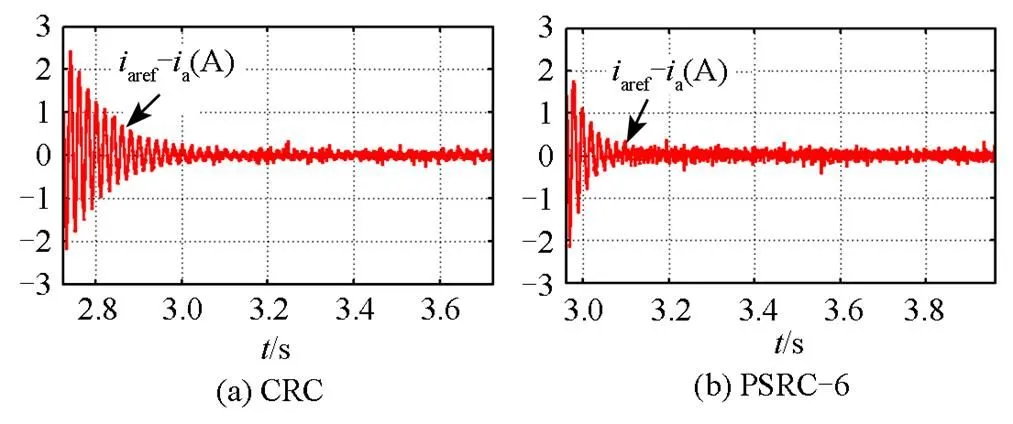
图11 加入RC后三相逆变并网系统电流误差收敛波形图

图12 加入RC后单相逆变并网系统电流误差收敛波形图

4 结论

将PSRC应用于恒压恒频PWM并网变流系统，包括三相/单相整流和三相/单相逆变并网系统中，实验结果验证了PSRC的有效性和优越性。

1) 在三相/单相PWM整流系统中，PSRC都使电压、电流间的相位差得到补偿，从而实现了单位功率因数和电流的精确控制；并且，相对CRC，PSRC都能使电流的误差收敛速率得到大幅提高，最快能够接近CRC的三倍(三相)和两倍(单相)，从而实现了电流的快速控制。

2) 在三相/单相PWM逆变并网系统中，PSRC都能使电流的畸变得到明显改善，从而实现了电流的精确控制；并且，相对CRC，PSRC都能使电流的误差收敛速率得到大幅提高，最快能够接近CRC的三倍(三相)和两倍(单相)，从而实现了电流的快速控制。

总之，PSRC实现了PWM并网变流系统的并网电流快速、精确控制，为“净化”电力系统中电力电子接口提供了一种高性能电流控制策略。

[1] FRANCIS B A, WONHAM W M. The internal model principle of control theory[J]. Automatica, 1976, 12(5): 457-465.

[2] COSNER C, ANWAR G, TOMIZUKA M. Plug in repetitive control for industrial robotic manipulators[C] // IEEE International Conference on Robotics and Automation, Cincinnati, OH, 1990: 1970-1975.

[3] ZHOU K, WANG D, ZHANG B, et al. Plug-in dual- mode-structure repetitive controller for CVCF PWM inverters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 784-791.

[4] ZHOU K, WANG D, ZHANG B, et al. Dual-mode structure digital repetitive control[J]. Automatica, 2007, 43(3): 546-554.

[5] COSTA-CASTELLO R, GRINO R, FOSSAS E. Odd-harmonic digital repetitive control of a single-phase current active filter[J]. IEEE Transactions on Power Electronics, 2004, 19(4): 1060-1068.

[6] ESCOBAR G, HERNANDEZ-BRIONES P G, MARTINEZ P R, et al. A repetitive-based controller for the compensation of 6l±1 harmonic components[J]. IEEE Transactions on Industrial Electronics, 2008, 55(8): 3150-3158.

[7] ZHOU K, LOW K, WANG D, et al. Zero-phase odd-harmonic repetitive controller for a single-phase PWM inverter[J]. IEEE Transactions on Power Electronics, 2006, 21(1): 193-201.

[8] LU W, ZHOU K, WANG D, et al. A generic digital nk±m order harmonic repetitive control scheme for PWM converters[J]. IEEE Transactions on Industrial Electronics, 2014, 61(3): 1516-1527.

[9] LU W, ZHOU K, CHENG M, et al. A novel 6k±1 order harmonic repetitive control scheme for CVCF three-phase PWM inverters[C] // International Conference on Electrical Machines and Systems, Beijing, 2011: 1-4.

[10] LU W, ZHOU K, WANG D, et al. A general parallel structure repetitive control scheme for multiphase DC- AC PWM converters[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3980-3987.

[11] LU W, ZHOU K, WANG D. General parallel structure digital repetitive control[J]. International Journal of Control, 2013, 86(1): 70-83.

[12] ZHOU K, WANG D. Digital repetitive controlled three- phase PWM rectifier[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 309-316.

[13] 杨俊伟, 史旺旺. 交流电流直接控制的单相 PWM 整流器非线性控制策略[J]. 电力系统保护与控制, 2015, 43(20): 114-118.

YANG Junwei, SHI Wangwang. Nonlinear control strategy for direct AC current control in single-phase PWM rectifier[J]. Power System Protection and Control, 2015, 43(20): 114-118.

[14] 尹璐, 赵争鸣, 张凯, 等. 一种考虑系统非理想特性的三相电压型 PWM 整流器控制参数设计方法[J]. 电工技术学报, 2015, 30(23): 10-17.

YIN Lu, ZHAO Zhengming, ZHANG Kai, et al. A regulator design method for three-phase voltage-source PWM rectifiers considering the non-ideal characters of the control system[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 10-17.

[15] 王萌, 施艳艳, 沈明辉, 等. 三相电压型整流器模型电压预测控制[J]. 电工技术学报, 2015, 30(16): 49-55.

WANG Meng, SHI Yanyan, SHEN Minghui, et al. Model voltage predictive control for three-phase voltage source rectifier[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 49-55.

[16] 郭小强, 贾晓瑜, 王怀宝, 等. 三相并网逆变器静止坐标系零稳态误差电流控制分析及在线切换控制研究[J]. 电工技术学报, 2015, 30(4): 8-14.

GUO Xiaoqiang, JIA Xiaoyu, WANG Huaibao, et al. Analysis and online transfer of stationary frame zero steady-state error current control for three-phase grid-connected inverters[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 8-14.

[17] 雷亚雄, 李建文, 李永刚. 基于准PR调节器电流双闭环LCL三相并网逆变器控制[J]. 电力系统保护与控制, 2014, 42(12): 44-50.

LEI Yaxiong, LI Jianwen, LI Yonggang. Control strategy of three-phase LCL grid-connected inverter based on quasi-PR adjuster[J]. Power System Protection and Control, 2014, 42(12): 44-50.

[18] 赵贵龙, 曹玲玲, 祝龙记. 基于光伏并网逆变系统的改进锁相环设计[J]. 电力系统保护与控制, 2015, 43(2): 108-112.

ZHAO Guilong, CAO Lingling, ZHU Longji. Improved PLL design of PV grid inverter system[J]. Power System Protection and Control, 2015, 43(2): 108-112.

[19] 翦志强, 司徒琴. 三相电压不对称跌落光伏并网逆变器控制方法[J]. 电力系统保护与控制, 2015, 43(14): 126-130.

JIAN Zhiqiang, SITU Qin. Control method of photovoltaic grid-connected inverter under three-phase voltage unbalanced dips[J]. Power System Protection and Control, 2015, 43(14): 126-130.

[20] GRADSHTEĬN I S, RYZHIK I M, JEFFREY A, et al. Table of integrals, series, and products[M]. 7th ed. San Diego, CA: Academic Press, 2007.

[21] LU W, ZHOU K, YANG Y. A general internal model principle based control scheme for CVCF PWM converters[C] // The 2nd IEEE International Symposium on Power Electronics for Distributed Generation Systems, Hefei, 2010: 485-489.

[22] AKAGI H, WATANABE E H, AREDES M. Instantaneous power theory and applications to power conditioning[M]. Hoboken: Wiley, 2007.

(编辑 魏小丽)

Parallel structure repetitive controller for PWM grid-connected converters

LU Wenzhou1, ZHOU Keliang2, CHENG Ming3, SHEN Jinfei1

(1. Key Laboratory of Advance Process Control for Light Industry, Ministry of Education, Jiangnan University,Wuxi 214122, China; 2. School of Engineering, University of Glasgow, Glasgow G12 8QQ, Scotland, UK; 3. School of Electrical Engineering, Southeast University, Nanjing 210096, China)

On the basis of “cleaning” the power electronics interfaces in power system, and in order to achieve fast and accuracy grid currents tracking the references, parallel structure repetitive control (PSRC) and its control system are discussed. PSRC employs a parallel combination of categorized+(=0,1,2,…,-1) order harmonic frequency internal models to achieve the zero-error tracking or disturbance elimination for all harmonics. Compared with conventional RC (CRC), PSRC has less time delay, faster error convergence rate, same tracking accuracy and same digital data memory cells. PSRC is applied into constant-voltage constant-frequency (CVCF) pulse-width-modulation (PWM) converter system, including three/single-phase rectifier/grid-connected inverter systems. Experimental results validate the effectiveness and advantages of PSRC. This work is supported by National Natural Science Foundation of China (No. 51407084) and Fundamental Research Funds for the Central Universities (No. JUSRP11461).

internal model principle (IMP); repetitive control (RC); parallel structure; pulse-width-modulation (PWM); grid-connected converter

10.7667/PSPC151905

国家自然科学基金项目(51407084)；中央高校基本科研业务费专项资金项目(JUSRP11461)

2015-10-29；

2016-01-26

卢闻州(1983-)，男，通信作者，博士，副教授，研究方向为电力电子与电力传动、新能源发电与控制技术；E-mail:luwenzhou@126.com 周克亮(1970-)，男，博士，教授，研究方向为电力电子与电力传动、新能源发电、控制理论和应用、智能电网技术；E-mail: Keliang.Zhou@glasgow.ac.uk 程 明(1960-)，男，博士，教授，研究方向为微特电机及测控系统、新能源发电、电动汽车驱动控制。E-mail: mcheng@seu.edu.cn