基于自组织临界理论的电网脆弱线路辨识

岳贤龙，王 涛，顾雪平，李 凯，张 尚，王铁强



基于自组织临界理论的电网脆弱线路辨识

岳贤龙1，王 涛1，顾雪平1，李 凯1，张 尚1，王铁强2

(1.华北电力大学新能源电力系统国家重点实验室，河北 保定 071003；2.河北电力调度通信中心，河北 石家庄 050021)

为了辨识引发电力系统连锁故障的脆弱线路，从事故发展的角度出发，基于自组织临界理论的幂律特性构建了电网脆弱线路辨识模型。线路因保护的隐藏故障或过载而退出运行后，利用孤岛搜索辨识引发系统解列的关键线路，并对其处理以便重新潮流计算。综合改进的潮流分布熵、灵敏度分析理论及OPF模型对负荷水平和发电机出力进行调整，构成电网停电模拟模型。通过大量的仿真与统计，利用系统负荷损失量的幂律或幂律尾特性判断系统是否达到临界状态，同时，系统负荷损失量的数学期望越高，该自组织临界状态越危险，致使连锁故障的风险越高。以IEEE 39节点系统为仿真算例，验证了方法的正确性和有效性。

脆弱线路；自组织临界理论；改进的潮流分布熵；停电模拟；孤岛搜索；灵敏度分析

0 引言

电网的大规模互联已成为国内外电力系统发展的必然趋势[1]，使得系统的动态行为变得越来越复杂[2-3]；同时，系统的发电和负荷水平不断提高，使得线路潮流逐渐增加[4-5]。当线路因过载或保护故障而退出运行后，将引发潮流不同程度的转移，继而可能引发更多线路相继断开，最终形成大停电连锁事故。因此，电网对于辨识脆弱线路的需求越来越强烈，从而降低连锁故障的发生概率。

“脆弱性”指一个系统、一个体制的薄弱环节，是当前的热点研究问题[6]。人们已经提出多种辨识电网脆弱线路的研究方法，但还没有形成广泛认可的理论方法和模型，主要分为以下两个方面，第一，从图论的角度出发，引入相关的电气量进行扩展和改进；第二，从连锁故障和潮流计算的角度入手，利用系统状态和行为的变化进行分析。

对于图论在脆弱线路辨识中的应用，一方面，对图论进行扩展和改进，以提高其在不同电网中的通用性；另一方面，引入了相关的静态或动态电气量，以提高其在实际电网中的应用。文献[7]说明了电网的小世界特性，并利用节点的度数以及边的介数辨识脆弱线路；文献[8]通过定义带权重线路介数对复杂网络理论进行改进，能够辨识出承担较小功率但是在电网拓扑中占据特殊位置的线路；文献[7-8]仅从网络拓扑的角度辨识脆弱线路，并未计及支路阻抗等电气因素，与实际运行情况有较大差异。文献[9]基于电气介数指标辨识电网脆弱线路，综合考虑了发电容量和负荷水平的限制，更符合电力系统的物理背景，但是对系统状态的评估略显粗糙；文献[10-11]分别基于潮流介数和输电介数指标辨识关键线路，能够适应不同运行方式下电网潮流分布，但未计及线路故障后系统的连通性；文献[12]基于复杂网络理论，结合线路电压等级和地理位置，并综合考虑潮流熵变化和节点电压偏移辨识城市电网脆弱线路，更逼近电网实际运行情况，对脆弱线路辨识具有重要意义。

连锁故障仿真和电网潮流分析主要利用线路投切或潮流转移对系统的影响辨识脆弱线路。文献[13]考虑了连锁过载和隐性故障，从初始故障支路出发，综合故障支路与其他支路之间的关联作用，以及对其他支路的敏感性指标，并基于聚类方法对脆弱区域划分与识别；文献[14]基于模拟连锁故障的隐性故障模型和风险理论，提出复杂电网的线路故障风险评估方法；文献[15]基于在线生成的事故链，提出了依托事故链风险指标的输电环节脆弱度评估方法；文献[16]基于事故链风险评估理论，综合考虑线路在事故链中的位置和造成事故的严重程度辨识对连锁故障产生重要影响的关键线路；文献[13-16]从动态的角度对电网脆弱环节进行分析与评估，较好地揭示了电力系统连锁故障的起因和发展过程。文献[17]从线路潮流转移对系统整体影响的角度出发，综合线路过负荷扰动和故障断线风险获取潮流转移熵和潮流分布熵，建立了基于潮流熵测度的线路综合脆弱辨识模型。

本文从事故发展的角度入手，基于系统连锁故障负荷损失过程，利用自组织临界理论的幂律特性建立了电网脆弱线路辨识模型。模型中考虑了保护的隐藏故障，若线路因故障或过载而退出运行，利用广度优先搜索理论进行孤岛搜索与处理；进一步，对于潮流转移引起的线路重载或过载，利用灵敏度分析理论和OPF模型调整负荷水平和发电机出力，进而形成了电力系统停电模拟模型，其中，针对传统潮流分布熵未计及线路自身物理背景的缺陷，提出了引入线路负载率后的改进潮流分布熵，以便于筛选对系统冲击较小的可调整节点；然后，基于系统总损失负荷量的幂律特性统计和辨识脆弱线路。最后，以IEEE 39节点系统为算例进行仿真和分析，验证了该方法的正确性和有效性。

1 自组织临界理论模型

1.1 自组织临界理论

“自组织”指系统由内部组织间的相互作用而自发地形成某种状态，而不是由任何外部因素控制所形成；“临界状态”指系统处于一种特殊的、灵敏的状态，微小的变化可以不断地放大，直至扩延到整个系统。换言之，不管系统初始时是什么条件，系统都可能达到该状态，而当系统达到此临界状态时，即使很小的扰动也会引起整个系统发生一系列连锁性灾变[18]，此时系统内的事件大小和频率之间呈现幂函数关系。现实生活中，它的适用范围在逐渐扩大，一方面，包括了自然界中现存的生态系统及数不胜数的子系统；另一方面，社会生活中诞生的经济系统、交通系统和电力系统等。

历次大停电事故分析表明，负荷损失累计概率分布符合幂律或幂律尾特性[19-20]，自组织临界理论逐渐被用来解释大停电事故机理[21]。自组织临界理论主要有平衡系统临界性、无标度性、幂律分布特性和鲁棒性。本文模型中主要使用了自组织临界理论的幂律分布特性，依据该特性判断系统是否达到自组织临界状态，其中，变量的累积分布函数表示如下。

此外，当电网处于不同自组织临界状态时，系统负荷损失量的数学期望越高，表明该自组织临界状态越危险，致使连锁故障的风险越高。

1.2 模型中的总负荷损失

在模型的自组织临界理论应用中，以系统总损失负荷量作为幂律特性的变量，主要包括以下三种情况。第一，在故障发展过程中未形成任何孤岛系统，先以故障前的总负荷量作为基准，再求取连锁故障停电模拟结束之后系统总负荷量，以初始值与负荷切除结束之后的差值作为系统损失负荷量；第二，在故障过程中形成了孤岛，但是小孤岛系统单独运行时仍可以收敛，此时，同第一种情况相似，只是故障后总负荷量变化为两个独立系统的总负荷之和；第三，在故障发展过程中形成了孤岛，而且经过发电机出力调整后小孤岛系统单独运行时不收敛，总负荷损失为形成的孤岛中所包括的总负荷量。

(3)

2 电力系统停电模拟模型

2.1 考虑保护的隐藏故障

世界上约75%的大停电事故与保护系统的不正确动作有关[22]。可见，继电保护的隐藏故障逐渐成为电力系统灾变的一种潜在机理，引起了人们越来越多的重视，也成为电力系统仿真模拟中不容忽视的因素。

继电保护隐藏故障指当系统正常运行时对系统没有影响，而当系统中某些内部组织发生变化时，就会被触发的一类故障，继而引起大面积的故障。目前，引发保护隐藏故障的主要原因可分为以下两类：第一，所设的定值不合理，如保护定值更新滞后而不适合当前运行方式等；第二，保护系统中硬件不合理，如元件有缺陷、通信系统故障等[23]。

保护隐藏故障包括单重隐藏故障和多重隐藏故障，其中单重隐藏故障发生的概率比较小，而多重隐藏故障发生的概率更小，本模型仅考虑单重隐藏故障。当某条线路因过负荷或故障而切除时，隐藏故障会使得与该线路两端相连的所有线路以一定的概率断开，而单重隐藏故障会使得所有相连线路中至多断开一条[24]。

模型中保护隐藏故障按如下方法仿真，当模型中选择的某条线路断开后，将一组(0~1)范围内的随机连续均匀分布的数组分别赋予和该线路相连的所有线路，若线路赋值在0~0.02之间，则选择将该线路断开，否则，不予断开。总之，当已选择的线路断开后，以一个较小的概率定值断开与它相连接的所有线路，从而模拟了保护隐藏故障对系统的影响。

2.2 孤岛搜索与处理

对电力系统而言，由发电机、负荷和输电线路构成的电网可等效为复杂的节点图[25]。实际运行时，因线路过载或故障而导致线路被切除，可能引起系统解列而形成孤岛，致使潮流不平衡，进而影响系统潮流的准确计算。因此，需要及时搜索系统中形成的孤岛、调整孤岛中的发电机出力和负荷水平，既可以使系统达到新的平衡状态，又能够辨识出致使系统解列的重要线路。

孤岛搜索算法可用于判断某条支路断开后系统是否会产生孤岛。首先，以该支路的一个节点作为根节点，对其进行存储；然后，从节点出发，通过遍历所有支路依次搜索与连通的节点，并存储各个邻接点，此时，为母节点；接着，与上一步操作相同，依次搜索所有邻接的尚未访问的顶点即子节点，再从这些被访问的顶点出发，逐次访问与它们连接且未访问过的顶点，直至搜寻不到任何相通的节点为止；最后，若可连通节点数与系统初始的总节点数不相同，则表明系统中形成了孤岛，反之，则未形成孤岛。

孤岛搜索完毕后，如果形成了孤岛系统，分以下两种情况进行处理。若孤岛系统由少数几个节点构成，按照文献[5]中孤岛处理方法调整发电机出力和负荷水平；若两个解列后系统所包含的节点数目相当，按照2.3节中方法分别进行处理。此外，对每一次所留下来的、待处理的主要系统，将孤岛搜索结果中保存的节点数目作为参考，保留在所保存节点范围内的负荷节点数据、发电机节点数据，以及所有两个节点均在所保存节点范围之内的支路，继而方便于重新计算系统的潮流。

2.3 电力系统切负荷模型

线路在长期过负荷情况下对系统会产生一系列的影响，当线路温度超过最高允许工作温度后，可能引起线路短路着火而退出运行，线路的开断又将导致大量潮流转移到其他线路。其中，在电力系统安全稳定控制中，切机与切负荷控制是目前较为成熟的紧急控制措施。因此，在系统运行过程中，对与过载线路紧密相关的负荷进行合理的切除对系统的正常运行有着至关重要的作用。

2.3.1 改进的潮流分布熵

传统的潮流分布熵指节点受到负荷冲击后引起的系统中线路潮流分布的变化，进而评估其对系统安全运行带来的影响[17]。可见，其仅考虑了潮流分布不均匀对系统的影响，并未计及线路自身的物理背景，因此，综合考虑线路负载率提出了改进的潮流分布熵，以便于选取负荷调整后对系统影响较小的负荷节点。

线路的负载率定义为

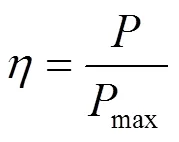
系统在正常运行状态下，当节点受到负荷冲击后，线路的负载率变化量为

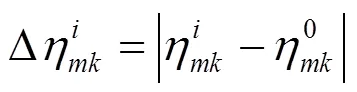
节点受负荷冲击后，对系统潮流冲击总量为

式中，为系统中线路总数。

线路因节点负荷冲击引起潮流转移的冲击比率为

(8)

2.3.2 节点负荷对线路潮流的灵敏度

式中：各参数可划分为状态变量与控制变量两种，状态变量表示为；控制变量表示为。其中，下标L表示PQ节点；g表示PV节点；v表示平衡节点。综合状态变量和控制变量，灵敏度分析的数学表达式定义如下

(10)

忽略不计控制向量之间的相互影响，对上式中控制向量求全微分，则灵敏度公式转化为

对上式整理，则灵敏度的矩阵表达式为

(12)

利用直流潮流法，线路潮流可通过线路首末节点电压的相角差与线路电抗得到，即

结合式(12)和式(13)，各节点有功出力或负荷对线路潮流的灵敏度为

2.3.3 电力系统的负荷调整过程

对于负荷水平和发电机出力的调整过程，本文重点分析节点负荷水平的调整方法，同时，采用直流模型计算最优潮流(OPF)，进而确定系统内机组出力[26]。负荷水平调整过程由切除顺序与切除量两个因素共同决定。对于切除顺序，利用2.3.1节所述的改进潮流分布熵指标选择对系统影响较小的可调整负荷节点1(1,2,,r)，然后利用2.3.2节中灵敏度分析方法获得排序的可调整节点集2(1,2,,t)，从而使得系统调整量最小。

实际调整过程中，负荷切除量由待降低的线路潮流和其对应的所有节点的灵敏度共同决定。对于PV节点，需要调整有功功率，调整量为；对于PQ节点，依据节点自身恒功率因数调整，同时调整有功功率和无功功率，有功功率调整量为，无功功率调整量为cot。考虑到切负荷实际操作的复杂性，线路重载或过负荷紧急控制下不能对所有节点的功率同时进行调整[27]，模型尽量减少涉及到的节点数目。在约束条件(15)下，按照有序的调整节点集2(1,2,,t)切负荷，从节点1开始分配调整量，如果未分配完毕，则选择2，依此类推，直至分配完毕，负荷分配流程如图1所示。系统功率调整完成后，判断系统中是否有线路过负荷，如果系统中不再有线路过载，则说明线路过载情况处理成功；如果系统中依然有线路过载，则重新对系统中的节点进行切负荷处理。

图1 负荷调整量分配流程

Fig. 1 Distribution flow chart of the load adjustment quantity

3 脆弱线路辨识流程

脆弱线路辨识流程如图2所示，该方法主要包括以下步骤：

(1) 读入电网某一时间断面的参数数据，统计系统总负荷量，设置快过程仿真次数max。

(2) 设置初始故障，断开脆弱性待评估的线路，将该线路从系统参数数据中删除，判断是否形成孤岛，若形成孤岛系统，则按照2.2节中的方法处理，否则，进入步骤(3)。

(3) 按照2.1节中方法随机均匀抽样断开与初始故障线路相连的某一条线路，并将选中线路从系统参数数据中删除，判断是否形成孤岛，若形成孤岛系统，则按照2.2节中的方法处理，否则，进入步骤(4)。

(4) 计算系统潮流，判断是否存在过载线路，若存在，则按照2.3节中方法调整发电机出力和负荷水平，否则，计算本次连锁故障总损失负荷量。

图2 脆弱线路辨识流程

(5)判断仿真次数是否达到设定的max，若没有达到，则转到步骤(2)，否则，进入步骤(6)。

(6) 判断是否遍历完所有待评估的线路，若没有遍历完毕，则转入步骤(2)，否则，仿真结束。

4 算例分析

选取IEEE 39节点系统为算例，该系统含有10个PV节点，28个PQ节点，节点31为平衡节点，系统如图3所示。采用Matpower仿真计算，验证本文电网脆弱线路辨识模型的有效性和正确性。

通过仿真分析得到如下结果，表1列出了排序前10的脆弱线路和两端节点；表2中列出了退出运行后会形成孤岛的所有线路和两端节点。

图3 IEEE 39节点系统接线图

表1 排序前10脆弱线路

Table 1 Vulnerable lines of the previous 10

表2 形成孤岛的线路

对于断开后形成孤岛的线路27和32，使系统解列成一个大系统和一个小系统，其重要性不言而喻，直接关系到所承担负荷的正常运行。线路27退出运行后，形成的小系统中包含了发电机节点33和34、负荷节点20，自身可以单独运行，但是该条线路断开后将使系统损失较多的发电出力，当大系统中负荷冲击较大时，直接影响系统的电量供应；线路32退出运行后，形成的小系统中包含了发电机节点34、负荷节点20，发电机节点的最大发电功率为508 MW，负荷节点的负荷值为680 MW，内部供不应求，需要调整负荷水平，否则，不能单独运行。

按照第3节的脆弱线路辨识流程，分别对脆弱性最高的线路35、脆弱性最低的线路21、可形成孤岛的线路27进行仿真分析，基于自组织临界理论的幂律特性统计结果如图4所示，横坐标和纵坐标均为对数坐标，横坐标表示连锁故障后系统负荷损失量，纵坐标表示负荷损失累计概率。

由图4可知，对于线路35，系统负荷损失和累计概率表现出幂律尾特性，说明其断开将使得系统连锁故障发展到自组织临界状态；对于线路21，开始时有微弱的递减趋势，曲线尾部迅速下降，并未表现出幂律特性；对于线路27，一方面，其断开后原始系统解列成两个系统，对系统安全性非常重要，另一方面，负荷损失和累计概率统计快速下降之后，在尾部表现出幂律特性，进入自组织临界状态。

图4 不同故障下系统负荷损失量的分布特性

鉴于许多文献中采用IEEE 39节点系统进行仿真分析，选取了引入电气量改进的图论法、事故链仿真、电网潮流分析三类方法进行对比分析，进一步验证本文所构建模型的正确性。文献[15]基于事故链风险指标进行辨识，其侧重于分析事故过程的中间环节，依据该环节触发后对系统电压、频率和潮流转移的影响进行辨识，对在线应用有较大的价值；文献[28]主要采用容量介数指标进行辨识，其侧重于从网络拓扑结构的角度分析线路的重要性，易于寻找与电网联系紧密的线路；文献[29]主要采用潮流熵进行辨识，线路退出运行后引起系统潮流分布变化，利用该潮流冲击分析对电网的影响，具有明确的物理意义。采用不同方法的脆弱线路辨识结果如表3所示。

由表3可知，本文与其他三类方法的脆弱线路辨识结果不尽相同，但是本文辨识结果中可形成孤岛的重要线路16-19、19-20，以及前10中的7条在其他三类方法中均有包含，说明了本文基于自组织临界理论幂律特性的脆弱线路辨识模型的准确性和可靠性，排序的差异主要是由于不同方法的评估指标所考虑的侧重点不同造成的，本文方法侧重于线路退出运行对电网结构的影响和连锁故障对系统负荷损失总量的影响。其中，线路21-22、22-23、23-24处在母线16、21、22、23和24构成的环形回路中，对于线路21-22故障后，将由线路16-21单独承担负荷节点21的功率传输；对于线路22-23故障后，线路21-22单独承担发电机节点35的功率输出；对于线路23-24故障后，母线36、23、22、21和16链式连接，大大降低了系统的可靠性和安全性。可见，在系统负荷水平增大后，上述3条线路任意一条故障后，该线路潮流将转移到单一线路，对系统带来非常大的威胁。

此外，对于脆弱性较低的线路，其退出运行后，有不止一条线路可替代其工作，以保证系统正常运行。如线路11-12故障后，使得母线12失去作用，但不影响带负荷母线13和传输作用的母线11正常工作，并且这两条母线均有两条线路与其正常相通。

表3 不同方法脆弱线路辨识结果

注：**表示文献[28]中未列出的排序前10脆弱线路。

5 结论

电网脆弱线路的辨识对连锁故障预防控制具有重要的意义。本文从电网事故发展的角度入手，综合保护隐藏故障、孤岛搜索与处理、改进的潮流分布熵和灵敏度分析理论构建了连锁故障快速仿真过程，结合自组织临界理论的幂律特性，同时，在不同自组织临界态下，负荷损失的数学期望越高，系统发生连锁故障的风险越大，通过大量的仿真与统计分析构建了电网脆弱线路辨识模型。通过对IEEE 39节点系统算例的仿真与分析，验证了该方法的可行性和正确性，对系统运行人员辨识重点监视区域有重要的实用价值。但本文所构建模型基于大量的仿真与统计分析辨识脆弱线路，适合于离线仿真，对于电网脆弱线路在线辨识与预警方面的研究，将是下一步的研究方向。

[1] 肖雅元, 张磊, 罗毅, 等. 基于回路可靠性贡献指标的电网薄弱点分析[J]. 电力系统保护与控制, 2015, 43(15): 54-59.

XIAO Yayuan, ZHANG Lei, LUO Yi, et al. Grid weak point analysis based on loop contribution index of the reliability[J]. Power System Protection and Control, 2015, 43(15): 54-59.

[2] 蔡晔, 曹一家, 谭玉东, 等. 基于标准化结构熵的电网结构对连锁故障的影响[J]. 电工技术学报, 2015, 30(3): 36-43.

CAI Ye, CAO Yijia, TAN Yudong, et al. Influences of power grid structure on cascading failure based on standardstructure entropy[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 36-43.

[3] 赵娟, 申旭辉, 吴丽华, 等. 结合直流潮流模型的电网断面热稳定极限快速评估方法[J]. 电力系统保护与控制, 2015, 43(3): 97-101.

ZHAO Juan, SHEN Xuhui, WU Lihua, et al. Fast evaluation method on thermal stability limit of power grid cross- section with DC power flow model[J]. Power System Protection and Control, 2015, 43(3): 97-101.

[4] 刘小丽, 毛弋, 梁杉, 等. 基于综合介数的电网脆弱线路辨识[J]. 电力系统保护与控制, 2016, 44(2): 116-121.

LIU Xiaoli, MAO Yi, LIANG Shan, et al. Identification of vulnerable lines in power grid based on comprehensive betweenness index[J]. Power System Protection and Control, 2016, 44(2): 116-121.

[5] 曾凯文, 文劲宇, 程时杰, 等. 复杂电网连锁故障下的关键线路辨识[J]. 中国电机工程学报, 2014, 34(7): 1103-1112.

ZENG Kaiwen, WEN Jinyu, CHENG Shijie, et al. Critical line identification of complex power system in cascading failure[J]. Proceedings of the CSEE, 2014, 34(7): 1103-1112.

[6] 丁明, 过羿, 张晶晶, 等. 基于效用风险熵权模糊综合评判的复杂电网节点脆弱性评估[J]. 电工技术学报, 2015, 30(3): 214-223.

DING Ming, GUO Yi, ZHANG Jingjing, et al. Node vulnerability assessment for complex power grids based on effect risk entropy-weighted fuzzy comprehensive evaluation[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 214-223.

[7] FU L, HUANG W, XIAO S, et al. Vulnerability assessmentfor power grid based on small-world topological model[C] // Power and Energy Engineering Conference (APPEEC), 2010 Asia-Pacific. IEEE, 2010: 1-4.

[8] 曹一家, 陈晓刚, 孙可. 基于复杂网络理论的大型电力系统脆弱线路辨识[J]. 电力自动化设备, 2007, 26(12): 1-5.

CAO Yijia, CHEN Xiaogang, SUN Ke. Identification of vulnerable lines in power grid based on complex network theory[J]. Electric Power Automation Equipment, 2007, 26(12): 1-5.

[9] 王仁伟, 张友刚, 杨阳, 等. 基于电气介数的复杂电网脆弱线路辨识[J]. 电力系统保护与控制, 2014, 42(20): 1-6.

WANG Renwei, ZHANG Yougang, YANG Yang, et al. Vulnerable line identification of complex power grid based on electrical betweenness[J]. Power System Protection and Control, 2014, 42(20): 1-6.

[10] 梁才, 刘文颖, 但扬清, 等. 输电线路的潮流介数及其在关键线路识别中的应用[J]. 电力系统自动化, 2014, 38(8): 35-40.

LIANG Cai, LIU Wenying, DAN Yangqing, et al. Flow betweenness of transmission lines and its application in critical line identification[J]. Automation of Electric Power Systems, 2014, 38(8): 35-40.

[11] 张富超, 谢成荣, 沈立新, 等. 基于源流路径链和输电介数的电网关键线路辨识[J]. 电力系统保护与控制, 2015, 43(21): 7-12.

ZHANG Fuchao, XIE Chengrong, SHEN Lixin, et al. Identification of power grid critical lines based on path chains and transmission betweenness[J]. Power System Protection and Control, 2015, 43(21): 7-12.

[12] 蔡晔, 曹一家, 李勇, 等. 考虑电压等级和运行状态的电网脆弱线路辨识[J]. 中国电机工程学报, 2014, 34(13): 2124-2131.

CAI Ye, CAO Yijia, LI Yong, et al. Identification ofvulnerable lines in urban power grid based on voltage grade and running state[J]. Proceedings of the CSEE, 2014, 34(13): 2124-2131.

[13] 邓慧琼, 张颖. 一种考虑连锁过载和隐性故障的电网脆弱区域分析方法[J]. 河北科技大学学报, 2013, 34(1): 67-74.

DENG Huiqiong, ZHANG Ying. A method for distinguishing sensitive areas in power network based on hidden failure of relay cascading successive failures[J]. Journal of Hebei University of Science and Technology, 2013, 34(1): 67-74.

[14] 丁理杰, 刘美君, 曹一家, 等. 基于隐性故障模型和风险理论的关键线路辨识[J]. 电力系统自动化, 2007, 31(6): 1-5.

DING Lijie, LIU Meijun, CAO Yijia, et al. Power system key-lines identification based on hidden failure model and risk theory[J]. Automation of Electric Power Systems, 2007, 31(6): 1-5.

[15] 王安斯, 罗毅, 涂光瑜, 等. 基于事故链风险指标的输电脆弱度在线评估方法[J]. 中国电机工程学报, 2010, 30(25): 44-50.

WANG Ansi, LUO Yi, TU Guangyu, et al. Online transmission vulnerability assessment method based on the fault chain risk index[J]. Proceedings of the CSEE, 2010, 30(25): 44-50.

[16] 王涛, 高成彬, 顾雪平, 等. 基于事故链模型的电网关键线路辨识[J]. 高电压技术, 2014, 40(8): 2306-2313.

WANG Tao, GAO Chengbin, GU Xueping, et al. Critical lines identification of power grid based on the fault chain model[J]. High Voltage Engineering, 2014, 40(8): 2306-2313.

[17] 李勇, 刘俊勇, 刘晓宇, 等. 基于潮流熵测度的连锁故障脆弱线路评估及其在四川主干电网中的应用[J]. 电力自动化设备, 2013, 33(10): 40-46.

LI Yong, LIU Junyong, LIU Xiaoyu, et al. Vulnerability assessment based on power flow entropy for lines in cascading failures and its application in Sichuan backbone power grid[J]. Electric Power Automation Equipment, 2013, 33(10): 40-46.

[18] 刘文颖, 但扬清, 朱艳伟, 等. 复杂电网自组织临界态辨识物理指标研究[J]. 电工技术学报, 2014, 29(8): 274-280, 288.

LIU Wenying, DAN Yangqing, ZHU Yanwei, et al. Research on physical indicators to identify power system self-organized critical state[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 274-280, 288.

[19] CARRERAS B A, NEWMAN D E, DOBSON I, et al. Initial evidence for self-organized criticality in electric power system blackouts[C] // System Sciences, 2000. Proceedings of the 33rd Annual Hawaii International Conference on. IEEE, 2000: 6 pp.

[20] 于群, 郭剑波. 中国电网停电事故统计与自组织临界性特征[J]. 电力系统自动化, 2006, 30(2): 16-21.

YU Qun, GUO Jianbo. Statistics and self-organized criticality characters of blackouts in China electric power systems[J]. Automation of Electric Power Systems, 2006, 30(2): 16-21.

[21] CARRERAS B A, NEWMAN D E, DOBSON I. Evidence for self-organized criticality in a time series of electric power system blackouts[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2004, 51(9): 1733-1740.

[22] 杨明玉, 田浩, 姚万业. 基于继电保护隐性故障的电力系统连锁故障分析[J]. 电力系统保护与控制, 2010, 38(9): 1-5.

YANG Mingyu, TIAN Hao, YAO Wanye. Analysis of power system cascading failure based on hidden failures of protective relaying[J]. Power System Protection and Control, 2010, 38(9): 1-5.

[23] 施莉, 赵东成, 杨明玉. 关于继电保护系统中隐形故障的探讨[J]. 继电器, 2004, 32(5): 66-69.

SHI Li, ZHAO Dongcheng, YANG Mingyu. Discussion on hidden failures in relay protection of power systems[J]. Relay, 2004, 32(5): 66-69.

[24] 易俊, 周孝信. 考虑系统频率特性以及保护隐藏故障的电网连锁故障模型[J]. 电力系统自动化, 2006, 30(14): 1-5.

YI Jun, ZHOU Xiaoxin. Cascading failure model of power grids considering frequency response characteristics and hidden failures[J]. Automation of Electric Power Systems, 2006, 30(14): 1-5.

[25] 张国华, 张建华, 杨京燕, 等. 基于有向权重图和复杂网络理论的大型电力系统脆弱性评估[J]. 电力自动化设备, 2009, 29(4): 21-26.

ZHANG Guohua, ZHANG Jianhua, YANG Jingyan, et al. Vulnerability assessment of bulk power grid based on weighted directional graph and complex network theory[J]. Electric Power Automation Equipment, 2009, 29(4): 21-26.

[26] 龚媛, 梅生伟, 张雪敏, 等. 考虑电力系统规划的OPA模型及自组织临界特性分析[J]. 电网技术, 2014, 38(8): 2021-2028.

GONG Yuan, MEI Shengwei, ZHANG Xuemin, et al. An improved OPA model considering planning and self- organized criticality analysis[J]. Power System Technology, 2014, 38(8): 2021-2028.

[27] 姚峰, 张保会, 周德才, 等. 输电断面有功安全性保护及其快速算法[J]. 中国电机工程学报, 2006, 26(13): 31-36.

YAO Feng, ZHANG Baohui, ZHOU Decai, et al. Active power security protection of transmission section and its fast algorithm[J]. Proceedings of the CSEE, 2006, 26(13): 31-36.

[28] 何俊, 庞松龄, 禹冰, 等. 基于容量介数指标的电网脆弱线路识别[J]. 电力系统保护与控制, 2013, 41(8): 30-35.

HE Jun, PANG Songling, YU Bing, et al. Vulnerable line identification of power grid based on capacity betweenness index[J]. Power System Protection and Control, 2013, 41(8): 30-35.

[29] 李勇, 刘俊勇, 刘晓宇, 等. 基于潮流熵的电网连锁故障传播元件的脆弱性评估[J]. 电力系统自动化, 2012, 36(19): 11-16.

LI Yong, LIU Junyong, LIU Xiaoyu, et al. Vulnerability assessment in power grid cascading failures based on entropy of power flow[J]. Automation of Electric Power Systems, 2012, 36(19): 11-16.

(编辑 张爱琴)

Vulnerable line identification of power grid based on self-organizing critical theory

YUE Xianlong1, WANG Tao1, GU Xueping1, LI Kai1, ZHANG Shang1, WANG Tieqiang2

(1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003, China; 2. Hebei Power Dispatch and Communication Center, Shijiazhuang 050021, China)

In order to identify vulnerable lines which lead to cascading failure of power system, the identification model is proposed based on the power law characteristic of the self-organizing critical theory from the perspective of the developing trend of the accident. When line is out of service due to overload or hidden failures in protection system, critical lines causing power system separation can be found based on the island search method, and islands will be processed to be convenient to power flow calculation. The simulation model of power system blackouts is built considering the improved distribution entropy of power flow and the theory of sensitivity analysis to adjust load level, and the OPF model to adjust generator output. Through a lot of simulation and statistics, the power law or power law tail characteristic of loss load of power system can be used to determine whether the system reaches the self-organizing critical state. While the mathematical expectation of loss load is higher, the self-organized critical state is more dangerous, and the risk of cascading failure is higher. The effectiveness of this method in identifying vulnerable lines of power grid has also been verified by simulation results of IEEE 39-bus system. This work is supported by National Natural Science Foundation of China (No. 51277076) and Fundamental Research Funds for the Central Universities (No. 13MS108).

vulnerable line; self-organizing critical theory; improved distribution entropy of power flow; blackout simulation; search islands; sensitivity analysis

10.7667/PSPC152138

国家自然科学基金资助项目(51277076)；中央高校基本科研业务费专项资金资助项目(13MS108)

2015-12-08；

2016-01-29

岳贤龙(1991-)，男，通信作者，硕士研究生，研究方向为电力系统安全防御与恢复控制；E-mail: yue15230237661@163.com 王 涛(1976-)，男，博士，副教授，研究方向为电力系统安全防御与恢复控制、复杂网络理论及其应用；顾雪平(1964-)，男，博士，教授，博士研究生导师，研究方向为电力系统安全防御和系统恢复、电力系统安全稳定评估与控制、智能技术在电力系统中的应用。