负折射率材料的实现模式及传输衰减分析

董焱章，刘书田

（1.湖北汽车工业学院汽车动力传动与电子控制湖北省重点实验室，湖北十堰442002；2.大连理工大学工业装备结构分析国家重点实验室，辽宁大连116024）

负折射率材料的实现模式及传输衰减分析

董焱章1，刘书田2

（1.湖北汽车工业学院汽车动力传动与电子控制湖北省重点实验室，湖北十堰442002；2.大连理工大学工业装备结构分析国家重点实验室，辽宁大连116024）

推导了均匀材料折射率完整的解析表达式，并基于此按照材料导磁性、导电性和介电性的不同情形讨论了电磁波的传输模式，结果表明材料的导磁性和介电性是负折射率的必要条件；进而得到了实现负折射率的3种可能情形，即磁导率和介电常数至少一个参数为负值，与此同时传输衰减上升为负折射率材料的新挑战；虽然材料的导电性不是负折射率的决定因素，但导电性与材料的传输衰减关系密切。此外也探讨了零折射率材料的凋落波传输模式。

负折射率；零折射率；传输衰减；左手材料；超材料设计

从场的角度来看，左手超材料的介电常数ε和磁导率μ均为负值，此时折射率n也相应地取负值；负折射率的典型体现是负折射［1］，同时负折射也是左手超材料逆斯涅尔定律的直接结果，由于在第一时间有力地证实了左手超材料的存在［2］，负折射率成为人们研究最多的左手超特性［3-7］，甚至在很大程度上，负折射率材料就等同于左手超材料。负折射率是左手超材料最重要的特异性能，它决定了左手超材料的其他奇异特性，如超分辨率成像［8-13］、光子隧穿效应［14］等。

负折射率是一种新颖的电磁新属性，目前仅存在于人工制备的左手超材料中［15-18］；尽管如此，介电常数ε和磁导率μ的双负性只是负折射率的充分非必要条件，自然界中天然物质或者其他人工超材料同样有实现负折射率的可能；若能从更一般的途径获得负折射率属性，那将对负折射率的工程应用具有重要的现实意义。因此，本文中首先推导了均匀材料折射率关于介电常数ε和磁导率μ的完整表达式，接着根据材料导磁性、导电性和介电性的不同分别从理论上阐释了产生负折射率的可能性，最后讨论了相应情形下电磁波的传输衰减问题。

1　折射率的完整表达式

詹姆斯·克拉克·麦克斯韦于1873年建立了电场与磁场的定律，若采用三维空间中的电磁场矢量符号表示，则微分形式的麦克斯韦方程组为［19］

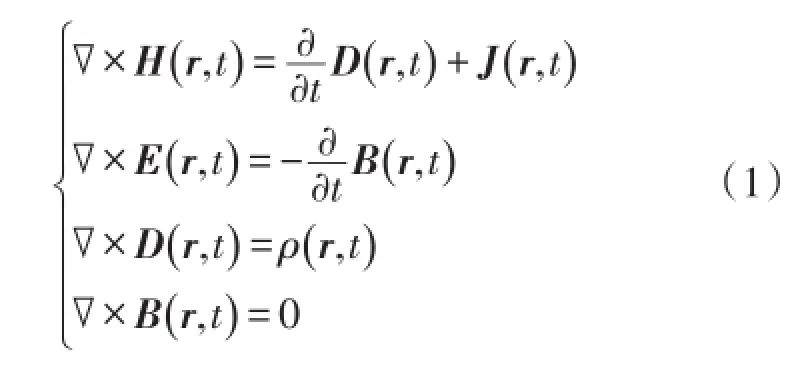
式中磁场强度矢量H、电位移矢量D、电流密度矢量J、电场强度矢量E、磁感应强度矢量B和净电荷密度ρ等电磁场物理量均是位置坐标矢量r和时间t的实变函数。假定传播材料为线性的、均匀的和各向同性的简单媒质，则电位移矢量D与电场强度矢量E、磁感应强度矢量B与磁场强度矢量H、电流密度矢量J与电场强度矢量E之间存在简单的本构关系：

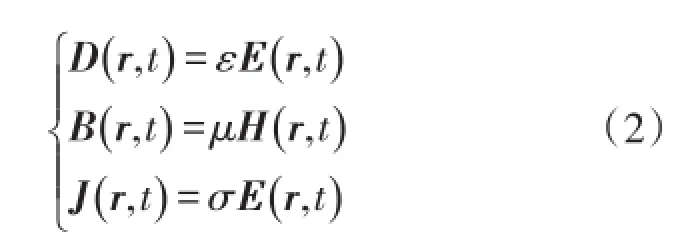
介电常数（电容率）ε、磁导率μ和电导率σ暂时未考虑电极化、磁化和导电过程中的影响因素。

一般传播材料的整体净电荷密度ρ为0，此时麦克斯韦方程组可以归结到一个关于电场强度矢量E的时域形式波动方程：

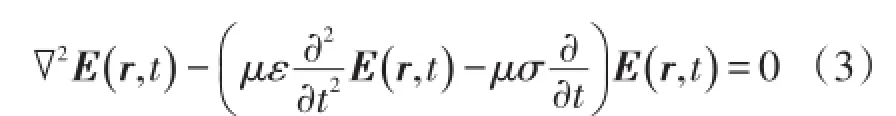
在简谐激励的情况下，可以引入一个正弦/余弦函数的电场强度矢量试探解：

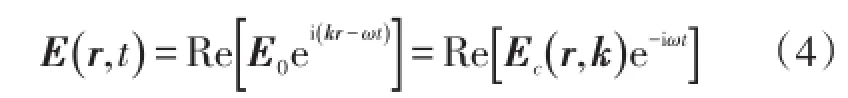
式中：Re［］为取其实部值的简写符号；E0为电场强度的实常数幅值矢量；Ec为关于位置坐标矢量r和波矢量k的电场强度的复数幅值矢量。将试探解（4）代入波动方程（3）可得一个关于电场强度复矢量Ec的频域形式波动方程：

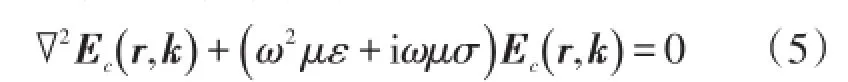
进而可以得到电磁波在材料中传播的色散方程：

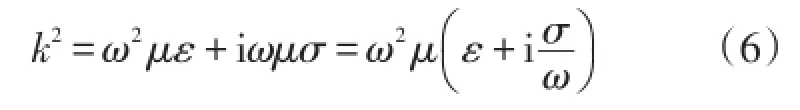
将该色散方程式中各本构参数用有效值符号表示，即可获得具有普遍意义的色散方程：

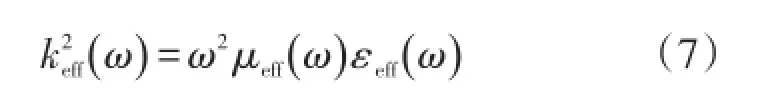
式（7）中3个有效电磁本构参数均为复数，其复数表达式为

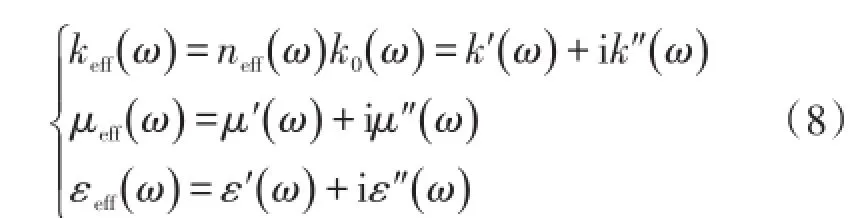
此处有效介电常数和有效磁导率考虑了电极化和磁化等影响因素，此外电导率σ的相关项已经被归入到有效介电常数虚部项的一部分。从式（7）～（8）可以推导出有效折射率的表达式：

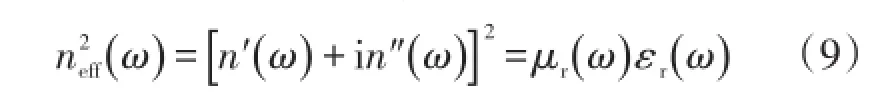
式中：r是指有效介电常数和有效磁导率除去真空项的相对值，通过复数的运算法则可以推导出有效折射率的实、虚部满足式（10）所示的方程组：

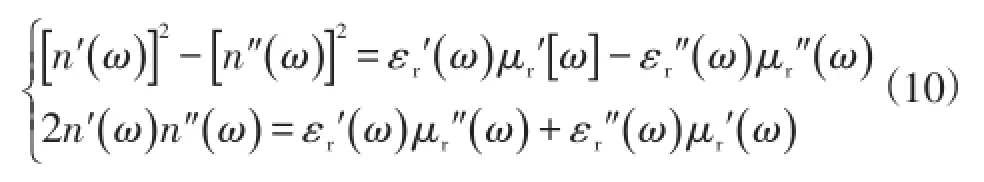
式中电磁本构参数的实虚部均为关于简谐激励频率ω的实变函数，为求表达式简洁，省略这个函数关系标记，且r和eff也将省略，如无特别说明，后面出现的介电常数和磁导率均指有效相对值形式。通过二次方程的求解，且根据折射率虚部的非负性可以最终获得折射率实、虚部的完整表达式：

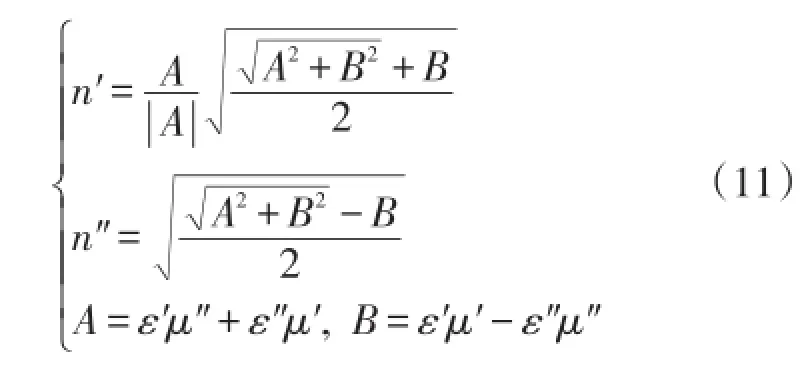
从折射率的实部表达式可以明显看出：只需A项小于0，就可以实现折射率的实部为负值，即通常所说的负折射率。

2　非磁性材料（μ′≈1和μ″≈0）

2.1绝缘材料（σ=0）

先从非磁性绝缘材料论述，对于这种相对简单的媒质，介电常数的实部和虚部严格满足Kram⁃ers-Kronig关系［20］：

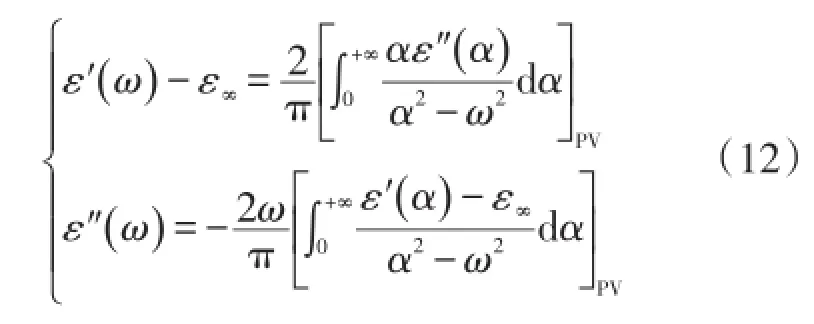
式中：［］PV为区间积分区间除去ω点的积分主值符号。一般地，可以认为无穷大频率处的介电常数ε∞与真空中的介电常数ε0相等，此时介电常数的虚部值为零；从式（12）可以直接推出零频率处的介电常数εs虚部值也为零，这符合介电常数奇函数的特性，零频率处的介电常数εs实部值是个有限大的值，即电学里常用的静态场介电常数，其可以通过查阅相应的材料参数表获知。

一般绝缘材料的介电常数虚部值非负，此时折射率的完整表达式（11）可以简化为

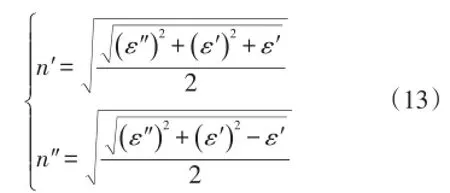
此时，材料的折射率实部值是非负的，即不存在负折射率的可能。在特殊情况下（ε′＜0且ε″=0）存在折射率实部为零的可能，但此时折射率虚部非零（sqrt（-ε′）），即零折射率的非磁性绝缘材料存在一定的传输衰减，但不会产生能量的耗散（μ″=0且ε″=0），仅仅是一种禁带传播模式——凋落波。除此情况之外，折射率实部均取正值。对于绝大多数绝缘材料（|ε′|量级设为1，则ε″＜10-1），分别对应2种传输模式：

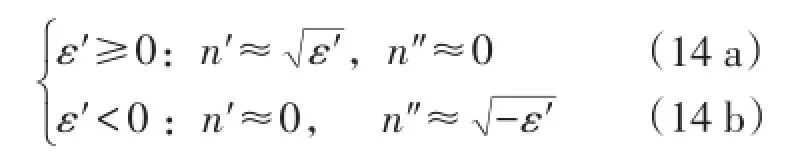
其中（14 a）近似无衰减的常规传输通带模式对应了自然界中大多数非磁性透波电介质；而（14 b）准凋落波传输禁带模式则对应了负介电常数材料，如电等离子体等。对于其他情况，传输模式为

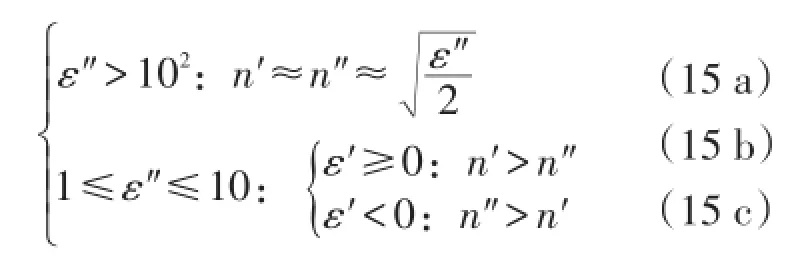
式中所列举的情形，其传输衰减都比较高，但目前尚未发现自然界中与之相对应的非磁性绝缘材料，工程上若要求高衰减超材料，则超高衰减模式式（15 a）将是不错的选择。

2.2导电材料（σ＞0）

此时，材料介电常数的实部和虚部不再严格满足Kramers-Kronig关系，介电常数的虚部多了一个电导率项：

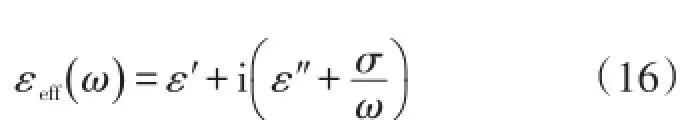
跟绝缘材料的差别也源于这个电导率项。值得注意的是零频率（ω=0）或者超导（σ=∞）情况下，介电常数的虚部值将趋于无穷大，这种现象在反演超材料电磁本构参数时经常遇到，这跟前面绝缘材料的“零频率时介电常数虚部值为零”有很大差别，问题出在电导率被人为地归入到介电常数的虚部项上。而无穷大频率（ω=∞）或者不导电（σ=0）情况下，电导率项的贡献为零，此时介电常数的虚部将退回到绝缘材料的情形。

如果不再区分电导率项和材料极化损耗项，把介电常数的虚部看作一个整体，那么其折射率的变化情形将类似绝缘材料的讨论结果，只不过导电材料的介电常数虚部值往往比较大（ε″≥1），式（15）所列举的传输模式对于导电材料将成为常态，跟导电引起的欧姆损耗密切相关。

此外还可按照导电和极化的情况分类讨论：低频率或者高电导率时，导电材料（如金属导体）具有很强的电磁屏蔽作用；而高频率或者低电导率时，导电材料可以在一定程度上被看做绝缘材料。

对于非磁性材料，无论是绝缘材料，还是导电材料都不存在负折射率的可能，但存在单负介电常数引起的凋落波禁带传输模式。

3　磁性材料（一般102＜　||μ′＜103）

3.1绝缘材料（σ=0）

此时，介电常数的实部和虚部严格满足Kram⁃ers-Kronig关系，前面所得的关于介电常数的定性结论仍然是成立的。若电的极化特性很弱（ε′=1 和ε″=0），那么折射率的情形完全类同非磁性绝缘材料，只是讨论对象由介电常数变成磁导率，这跟折射率完整表达式中介电常数和磁导率的对偶地位是一致的。此时磁性绝缘材料也不存在负折射率的可能，仅存在单负磁导率引起的凋落波禁带传播模式。如果电的极化因素不容忽略，则折射率的表达式需要退回到完整表达式式（11）。

1）介电常数和磁导率的实部均为非负值（ε′≥0和μ′＞0），由式（11）容易推知此时折射率的实部非负，即不存在负折射率的可能。此外，对于较小值的介电常数和磁导率虚部（ε″＜10-1和μ″＜1），折射率情形为

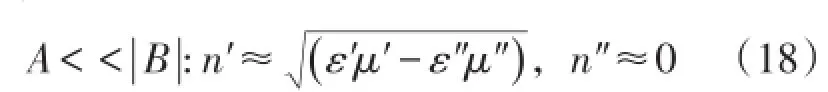
这种传输模式对应了大多数磁性透波电介质，具备极低衰减的常规传输通带。对于较大值的介电常数和磁导率虚部（ε″＞102和μ″＞104），折射率情形为

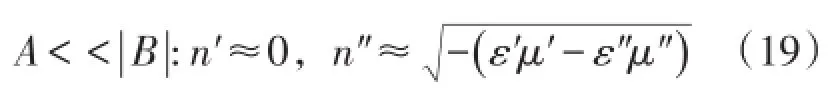
该情形属于准凋落波传输模式，目前尚未发现自然界中与之相对应的磁性绝缘材料。而对于其他情况，如介电常数和磁导率实虚部量级相同（1＜ε″＜10 和102＜μ″＜103），折射率情形为

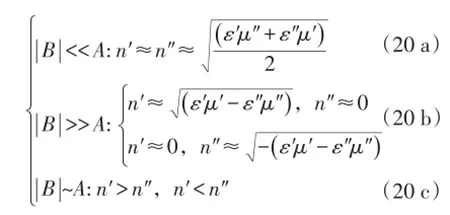
其中式（20 a）情形对应一定衰减的常规传输通带模式。式（20 b）情形的分支结果取决于B项的正负性：取正值则对应上支，即对应极低衰减的常规传输通带模式；取负值则对应下支，即对应准凋落波禁带传输模式。该分支判定规则同样适用于式（20 c）情形，区别在于式（20 c）情形分别对应较低或较高衰减的常规传输通带模式。

2）介电常数的实部非负而磁导率的实部为负（ε′≥0和μ′＜0），由式（11）容易推知此时折射率的实部可能取负值，即存在负折射率的可能。此外，鉴于此时B项的恒负性，由式（11）也可以推知此时折射率的虚部值总是大于其实部绝对值，即其品质因子（FOM）不高。具体折射率情形为

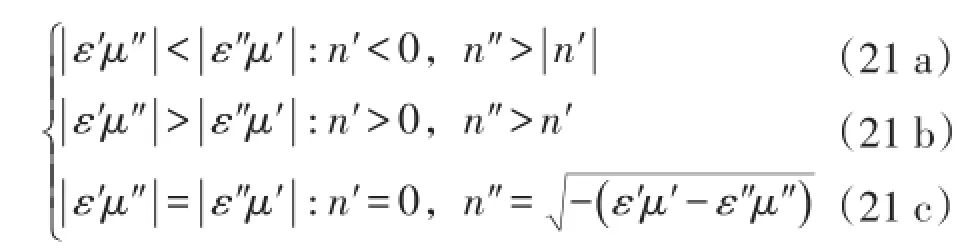
其中式（21 a）情形的负折射率对应由单负磁导率引起的左手传输模式，同时伴随较高的衰减。式（21 b）情形对应了较大衰减的常规传输模式，对于磁谐振型的负磁导率材料，这种传输模式是它的常态。式（21 c）情形对应凋落波禁带传输模式，属于过渡阶段的零折射率磁性绝缘材料，其更一般的准凋落波禁带传输模式为

3）介电常数的实部为负而磁导率的实部非负（ε′＜0和μ″＞0），类似单负磁导率材料，单负介电常数材料也存在负折射率的可能。此时，B项的值仍为恒负，即折射率的虚部值仍恒大于其实部绝对值。具体折射率情形为

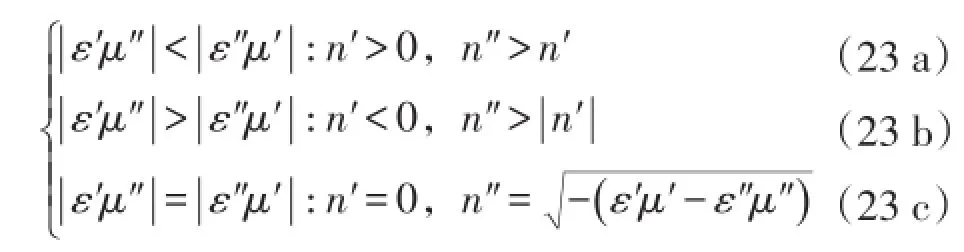
比较式（23）和（21）可以发现它们互为对偶情形，这依然跟折射率完整表达式中介电常数和磁导率的对偶地位相关。

4）介电常数和磁导率的实部均为负值（ε′＜0 和μ′＜0），这是左手材料的定义情形，目前尚未发现具有这种双负电磁本构参数的天然材料。尽管如此，从理论上容易判断此时的折射率实部值恒负，即负折射率将作为左手材料的固有属性存在。折射率完整表达式中介电常数和磁导率的对偶特性，加之“负负得正”的法则，双负材料的折射率变化情形将类似双正的常规材料，区别在于前者的折射率实部前多添了一个负号。具体情形为

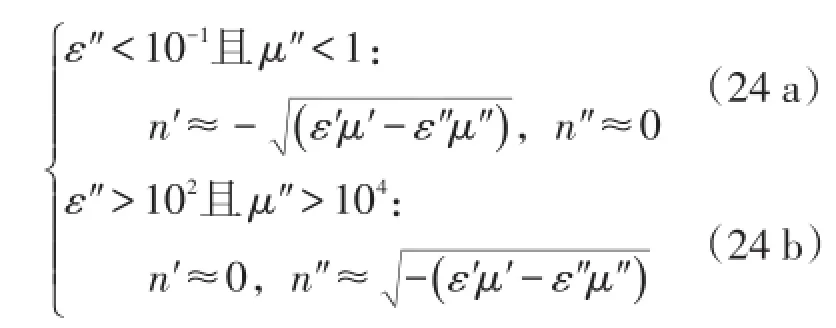
若追求高传输效率的左手材料设计，式（24 a）所示情形将是首选。而对于介电常数和磁导率实虚部量级相同等其他情况，折射率情形为

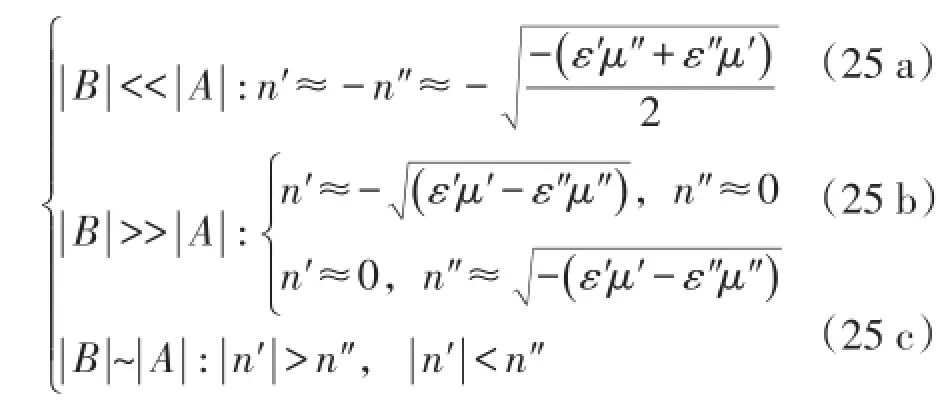
其中式（25 a）所示情形对应一定衰减的左手传输模式。类似式（20 b～c）情形的分支结果取决于B项的正负性：取正值则对应上支，即对应近似无衰减的左手传输模式（或较低衰减的左手传输模式）；取负值则对应下支，即对应准凋落波禁带传输模式（或较高衰减的左手传输模式）。

3.2导电材料（σ＞0）

同非磁性导电材料的讨论类似，电导率影响磁性材料的也仅仅是介电常数的虚部：零频率（ω=0）或者超导（σ=∞）情况下，电导率项的贡献远远超过了极化项，介电常数的虚部值将趋于无穷大；无穷大频率（ω=∞）或者不导电（σ=0）情况下，电导率项的贡献为零，问题将退回到磁性绝缘材料的情形。

若把介电常数的虚部看作一个整体，那么其折射率的变化情形也将类似磁性绝缘材料的讨论结果，只不过此时导电材料的介电常数虚部值比较大，式（19）所对应的准凋落波传输模式对于磁性导电材料将成为常态，式（21 a）、式（23 a）、式（25 a）所示情形也将变得更为可能，亦即伴随较大的衰减，这当然跟导电引起的欧姆损耗是密切相关的。

4　结论

对于均匀材料来说，材料的导磁性和介电性是负折射率的必要条件，同时产生负折射率还需要磁导率和介电常数至少一个为负值，尽管如此，单负电磁本构参数对应的负折射率虚部往往较大，这将导致其左手带宽的传输性能大打折扣；负折射率是左手材料（双负电磁本构参数）的固有属性，其左手传输的衰减水平取决于介电常数和磁导率的实虚部对比情况，虽然存在近似无衰减的左手传输模式可能，但其产生条件（ε″＜＜||ε′和μ″＜＜||μ′）所对应的材料尚未被发现。材料的导电性不是负折射率的决定因素，但会显著影响材料的介电常数虚部值，伴随导体而来的传输衰减，与导电引起的欧姆损耗是密切相关的。特殊情况下，材料折射率可以为零值，此时电磁波处于（准）凋落波传输模式。

［1］Pendry J B.Negative Refraction［J］.Contemporary Phys⁃ics，2004，45（3）：191-202.

［2］Shelby R A，Smith D R，Schultz S.Experimental Verifica⁃tion of a Negative Index of Refraction［J］.Science，2001，292（5514）：77-79.

［3］Smith D R，Schurig D，Pendry J B.Negative Refraction of Modulated Electromagnetic Waves［J］.Applied Physics Letters，2002，81（15）：2713-2715.

［4］Parazzoli C G，Greegor R B，Li K，et al.Experimental Ver⁃ification and Simulation of Negative Index of Refraction Using Snell′s Law［J］.Physical Review Letters，2003，90 （10）：7401-7404.

［5］Dong Z G，Xu M X，Lei S Y，et al.Negative Refraction with Magnetic Resonance in a Metallic Double-ring Meta⁃material［J］.Applied Physics Letters，2008，92（6）：4101-4103.

［6］Verhagen E，Waele R，Kuipers L，et al.Three-dimension⁃al Negative Index of Refraction at Optical Frequencies by Coupling Plasmonic Waveguides［J］.Physical Review Letters，2010，105（22）：3901-3904.

［7］Costa J T，Silveirinha M G，Alu A.Poynting Vector in Negative-index Metamaterials［J］.Physical Review B，2011，83（16）：5120-5127.

［8］Pendry J B.Negative Refraction Makes a Perfect Lens［J］.Physical Review Letters，2000，85（18）：3966-3969.

［9］陈龙，何赛灵，沈林放.含负折射率介质的多层结构中倏逝波传播及隧道效应的分析［J］.物理学报，2003，52 （10）：2386-2392.

［10］Fang N，Zhang X.Imaging Properties of a Metamaterial Superlens［J］.Applied Physics Letters，2003，82（2）：161-163.

［11］Smith D R，Pendry J B，Wiltshire M C K.Metamaterials and Negative Refractive Index［J］.Science，2004，305 （5685）：788-792.

［12］Pendry J B.Perfect Cylindrical Lenses［J］.Optics Ex⁃press，2003，11（7）：755-760.

［13］Veselago V G.Superlens as Matching Device［DB/OL］. ［2005-01-04］.http：//arxiv.org/abs/cond-mat/0501438.

［14］Liu R P，Cheng Q，Hand T，et al.Experimental Demon⁃stration of Electromagnetic Tunneling Through an Epsi⁃lon-near-zero Metamaterial at Microwave Frequencies ［J］.Physical Review Letters，2008，100（2）：3903-3906.

［15］Bi K，Zhou J，Zhao H J，et al.Tunable dual-band Nega⁃tive Refractive Index in Ferrite-based Metamaterials ［J］.Optics Express，2013，21（9）：10746-10752.

［16］Fruhnert M，Mühlig S，Lederer F，et al.Towards Nega⁃tive Index Self-assembled Metamaterials［J］.Physical Review B，2014，89（7）：075408.

［17］Sadatgol M，Özdemir Ş K，Yang L，et al.Plasmon Injec⁃tion to Compensate and Control Losses in Negative In⁃dex Metamaterials［J］.Physical Review Letters，2015，115（3）：035502.

［18］Townsend S，Zhou S W，and Li Q.Design of Fiber Meta⁃materials with Negative Refractive Index in the Infrared ［J］.Optics Express，2015，23（14）：18236-18242.

［19］孔金瓯.电磁波理论［M］.北京：电子工业出版社，2003.

［20］Toll J S.Causality and the Dispersion Relation：Logical Foundations［J］.Physical Review，1956，104（6）：1760-1770.

Analysis on Realization Modes and Transmission Attenuation of Negative Refractive Index Materials

Dong Yanzhang1，Liu Shutian2
（1.Hubei Key Laboratory of Automotive Power Train and Electronic Control，Hubei University of Automotive Technology，Shiyan 442002，China；2.State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian University of Technology，Dalian 116024，China）

The complete analytical expression of the refractive index was theoretically derived.Based on the expression，the transmission modes of electromagnetic wave were discussed in terms of different cas⁃es about permeability，conductivity and dielectricity.The results show that the permeability and dielec⁃tricity are necessary conditions of the negative refractive index；then three possible cases are obtained to generate a negative refractive index，that is at least permeability or permittivity is negative.At the same time，the transmission attenuation becomes a new challenge of the negative refractive index mate⁃rials.The conductivity is not a determining factor of the negative refractive index.However，there is a close relation between the conductivity and transmission attenuation.In addition，the transmission modes of the evanescent waves from the zero refractive index materials were discussed.

negative refractive index；zero refractive index；transmission attenuation；left-handed mate⁃rials；metamaterial design

O441

A

1008-5483（2016）02-0043-06

10.3969/j.issn.1008-5483.2016.02.011

2016-03-16

国家自然科学基金（11502075，11504102）；湖北省自然科学基金（2014CFB629）；湖北汽车工业学院博士科研启动基金（BK201501）

董焱章（1983-），男，山东诸城人，博士，从事工程力学、结构与多学科优化、超材料设计等方面的研究。E-mail：dongyz@huat.edu.cn