中心极限定理的形象化模拟及其应用

徐彬

（武昌首义学院基础科学部，湖北武汉430064）

中心极限定理的形象化模拟及其应用

徐彬

（武昌首义学院基础科学部，湖北武汉430064）

介绍了中心极限定理的基本理论，利用数学软件Matlab进行了定理的模拟演示，直观形象地展示了定理所反映的本质内容，并结合实例给出了定理在现实生活中的应用，阐明了定理的重要应用价值。

中心极限定理；Matlab；模拟；应用

中心极限定理是概率论的重要内容，是概率论与数理统计之间一个非常重要的承前启后的桥梁。中心极限定理是研究在一定条件下，大量独立随机变量和的极限分布为正态分布的一系列定理的总称，它不仅提供了计算独立随机变量和的分布的方法，同时解释了正态分布广泛存在的原因，并为解决实际问题时利用正态分布提出了理论依据。

中心极限定理的理论性较强，是教学中的难点，传统教学中大多以理论阐述为主，不易被学生深刻理解和掌握，为了激发学生的学习兴趣，提高教学效果，对课程进行一定的调整：一方面用数学软件Matlab对定理进行仿真模拟，对定理从不同角度进行演示，将抽象的内容用可视化的形式展现出来，便于定理的理解和记忆；另一方面在教学中列举一些实例，通过对实例的学习，让学生体会定理的实用价值。

1　相关定理

林德伯格-列维定理设随机变量X1，X2，…，Xn，…相互独立，服从同一分布，且具有数学期望和方差：则随机变量之和的标准化向量的分布函数Fn（x）对于任意x满足

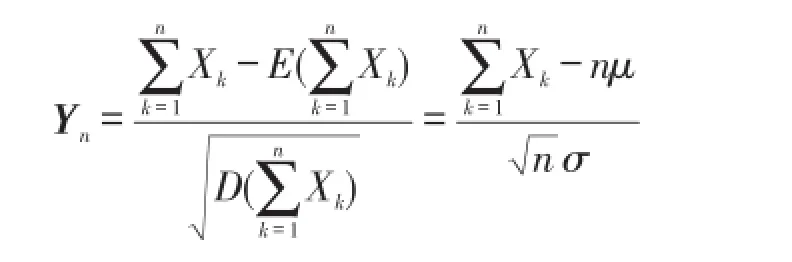
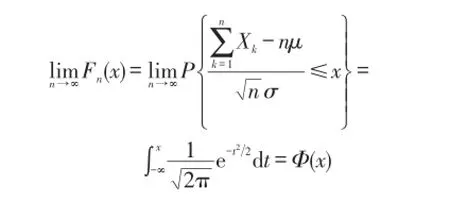
棣莫佛-拉普拉斯定理设随机变量ηn（n=1，2，…） 服从参数为n，p（0＜p＜1）的二项分布，则对于任意x，有

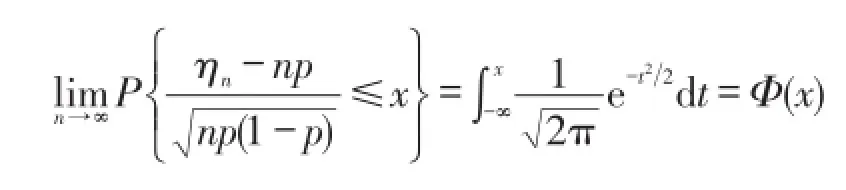
中心极限定理有多种形式，它们的结论相同，区别仅在于定理条件不同。本文中只列出常用的2个中心极限定理。林德伯格-列维定理（独立同分布的中心极限定理）是最常用的一种形式，揭示了独立同分布的随机变量和的极限分布是正态分布。棣莫佛-拉普拉斯定理是林德伯格-列维定理的特殊情况，是最早的中心极限定理，揭示了二项分布的极限分布是正态分布。在教学中可以按照历史发展顺序，先特殊后一般的认识规律安排中心极限定理的教学。

2　中心极限定理的Matlab演示

在中心极限定理的教学中，定理比较抽象，直接靠老师给出定理，证明其正确性，学生很难理解，引入数学实验后，可以让学生在实验中观察学习，将定理直观呈现出来，使课堂教学更加生动，有助于学生对定理的理解和掌握。

2.1棣莫佛-拉普拉斯定理（二项分布情形）

设随机变量X服从参数为n，p的二项分布，用Matlab演示二项分布B（n，当p）n增大时的演化过程，绘制二项分布（Bn， p），正态分布N（np，np（1-p））以及他们之间的误差函数图形，以p=3 4为例，编写Matlab程序如下：

图1中的“.”代表二项分布，“-”代表正态分布，“*”代表两者之间的误差。从n=5与n=50二项分布与相应的正态分布比较，可以看出：当n无限增大，二项分布的概率分布图逐渐逼近相应的正态分布的分布曲线；当n→∞时，误差函数几乎为零；2种分布几乎处处相等。

2.2林德伯格-列维定理（独立同分布情形）

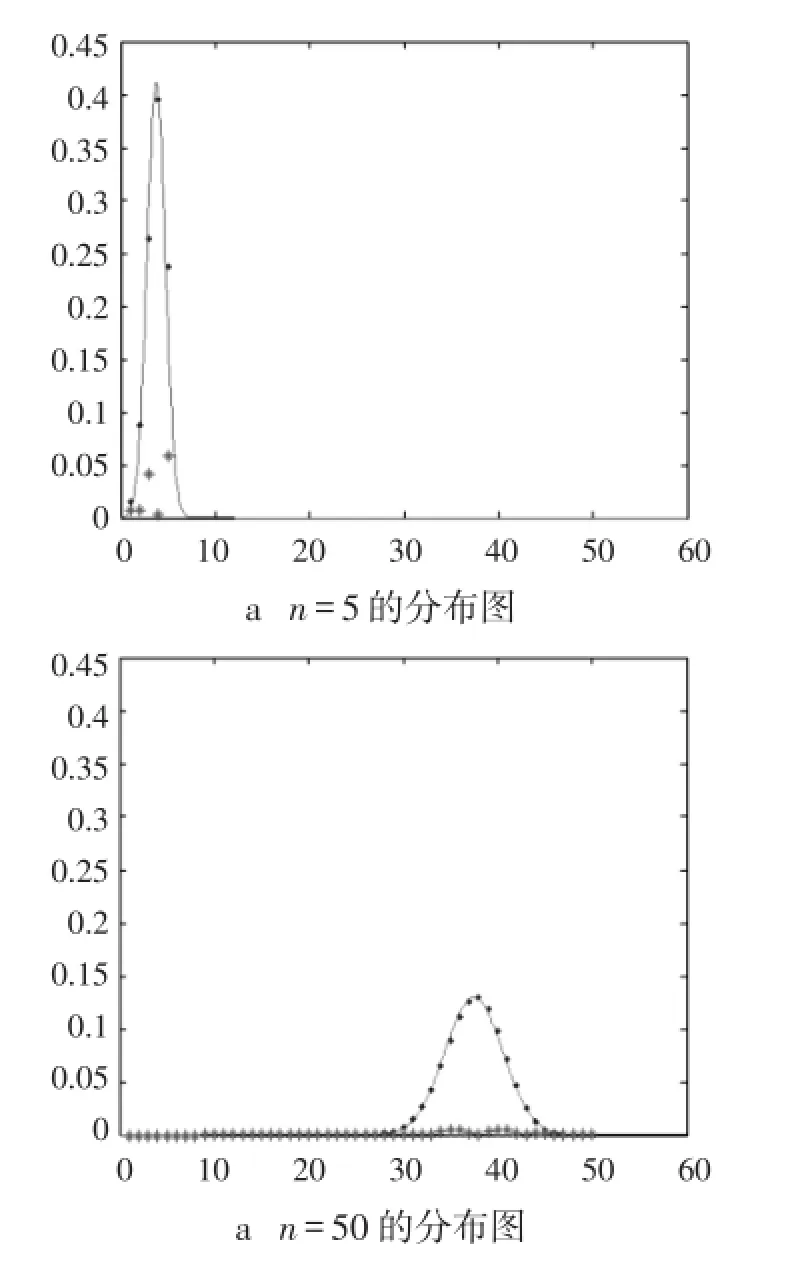
图1　二项分布与正态分布比较图

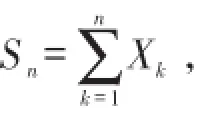
从图2中可以看出：当n=5，Sn的频率直方图呈现出“中间高、两边低”的特点，已有正态分布的雏形；当n=50，Sn的频率直方图更加接近于正态分布的图形，可以认为近似服从正态分布。

以指数分布为例，Matlab的演示过程解释了中心极限定理要表达的本质内容，可以让学生继续思考：对于其他分布是不是也可以得到相同的结论，试着编写相应的Matlab程序。这样学生既掌握了中心极限定理，同时激发了学生学习的兴趣，培养了学生的创新能力。

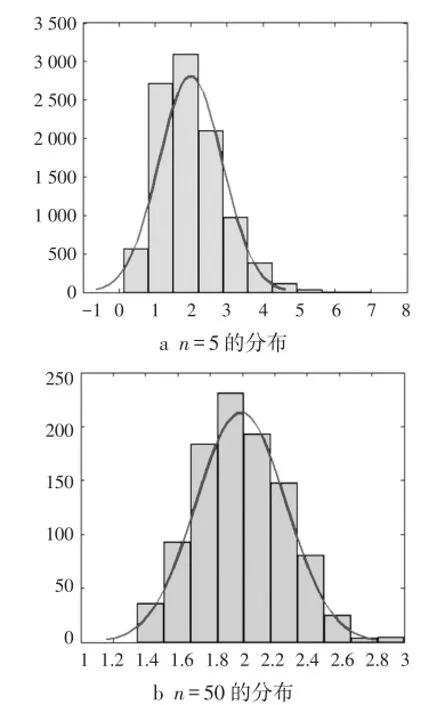
图2　Sn分布的频率直方图

3　中心极限定理的实际应用

中心极限定理不但可以解释客观现实中许多随机变量服从正态分布的原因，而且有着广泛的实际应用背景，在数理统计、管理决策、近似计算以及保险业等诸多领域中有重要的应用价值。

1）在幼儿园规模设置方面的应用

假设武汉某片区2所幼儿园的规模、师资配备、收费价格都相同。片区有500名适龄幼儿，假设每名幼儿选择幼儿园是相互独立的，问每个幼儿园应至少开设多少个班（每班30人）才能保证幼儿因缺少学位而离开的概率小于5%？

解：记X为500名幼儿选某幼儿园的人数，设幼儿园可接受s名幼儿入学。X服从二项分布B（500，0.5），算得EX=250，DX=125，由棣莫佛-拉普拉斯定理中心极限定理知近似服从标准正态分布N（0，1），因此

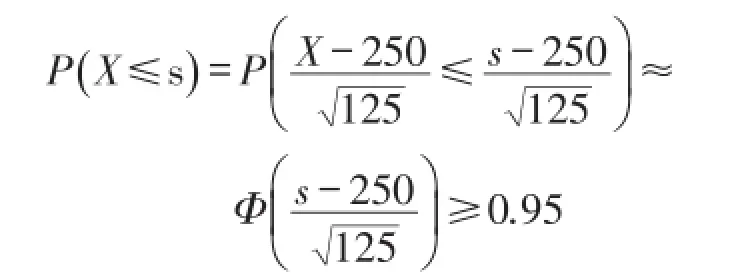
查标准正态分布表得解得s≥269。幼儿园每班容量为30人，269 30取整等于9，所以每个幼儿园至少开设9个班级，才能保证幼儿因缺少学位而离开的概率小于5%。

2）生产供应需求方面的应用

某学校教学楼每个教室都配备扩音设备，教师上课前需到值班室领取话筒和电池，为了保障教学工作的顺利进行，需要准备足够的电池。现有一批电池共100节，它们的寿命服从λ=1 30的指数分布，每次使用一节，用完即换新的，这批电池可使用2 500 h以上的概率是多少？

解：设每节电池的寿命为随机变量Xi，则X1，X2，…，X100相互独立，因为Xi服从λ=1 30的指数分布，则EXi=30，DXi=302，可求得

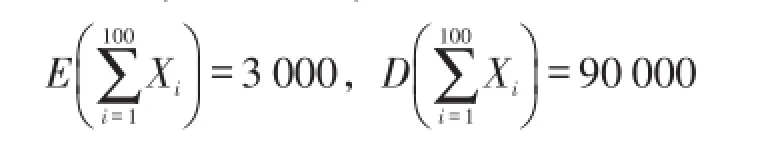
近似服从标准正态分布N（0，1），因此

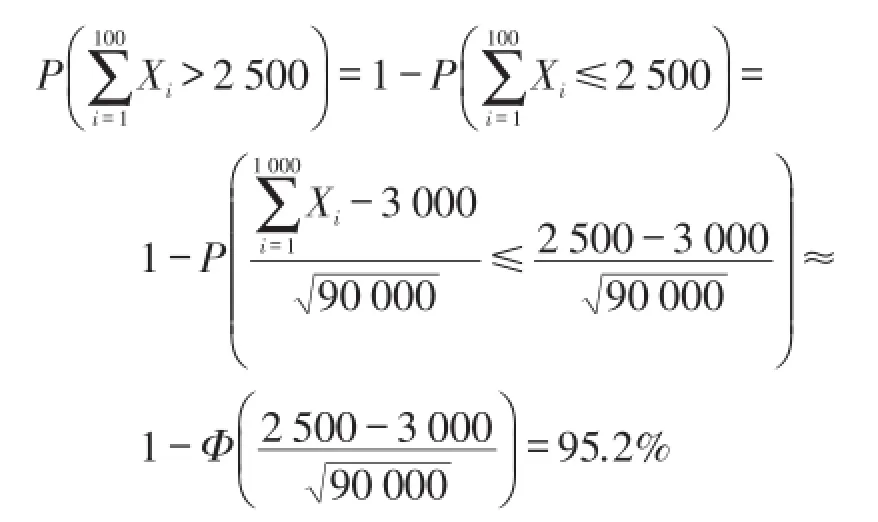
这批电池可使用2 500 h以上的概率是95.2%。

4　结语

中心极限定理是概率论的重要内容，也是数理统计的基石，有着承上启下的作用。中心极限定理内容抽象，学生不易理解掌握，在教学中，理论阐述的同时，可将数学实验引入课堂教学，利用Matlab等数学软件，把原本抽象难懂的知识变得直观形象，使教学过程形象生动；另外从解决实际问题入手，让学生真正体会定理的重要作用，激发学生探究知识的欲望，加深学生对定理本质的理解。

［1］盛骤，谢式千，潘承毅.概率论与数理统计［M］.4版.北京：高等教育出版社，2008.

［2］王静海，范恩贵.中心极限定理在抽样推断中的应用［J］.张家口师专学报（自然科学版），1994（1）：49-53.

［3］周德强.用Matlab辅助概率论极限理论教学［J］.高师理科学刊，2010，30（2）：89-91.

［4］林小萍.用Matlab模拟大数定理和中心极限定理［J］.汕头大学学报，2005，20（2）：12-18.

Simulation and Application of Center Limit Theorem

Xu Bin
（Department of Basic Science，Wuchang Shouyi University，Wuhan 430064，China）

The basic theory of the central limit theorem was introduced.The simulation of the theorem was carried out and the essential content of the theorem was visually demonstrated by using the software Matlab.The application of the theorem in real life was discussed through examples and the important application value of the theorem was elucidated.

center limit theorem；Matlab；simulation；application

O211

A

1008-5483（2016）02-0077-04

10.3969/j.issn.1008-5483.2016.02.018

2016-04-27

徐彬（1981-），女，山东昌邑人，硕士，从事应用数学方面的研究。E-mail：46569864@qq.com