不同曲率球面体入水砰击载荷数值计算

于龙超，闫发锁，赵九龙，王 淇

(1.哈尔滨工程大学，黑龙江 哈尔滨 150001; 2.沪东中华造船(集团)有限公司，上海 200129)

不同曲率球面体入水砰击载荷数值计算

于龙超1，闫发锁1，赵九龙2，王 淇1

(1.哈尔滨工程大学，黑龙江 哈尔滨 150001; 2.沪东中华造船(集团)有限公司，上海 200129)

从三维边界元方法出发，基于Wagner的自由液面抬升理论，采用数值仿真的方法研究了圆球入水的问题。通过数值模拟与轴对称体入水试验结果的正确性及适用性进行验证的基础上，并分析了不同半径的球体在不同速度下的入水总体受力和表面压力的变化规律。计算结果表明随着球体半径和入水速度的增加，峰值压力迅速增加，受力峰值与球体半径的平方和入水速度平方成正比关系；球体表面压力系数的分布计算结果表明，在测试点与水开始接触时压力系数最大，然后迅速减小；压力系数和入水速度无关，但和入水深度相关。

球体砰击；边界元法；受力峰值；压力系数

Abstract:Based on Wagner’s theory,the numerical simulation by 3D BEM method was used to study the slamming problem of spheres with different curvatures.The numerical results were validated by the test data from an axisymmetric body slamming test[11].The force acting on the body and the pressure at 5 specified locations are analyzed for the spheres with different radiuses and entry speeds.The result shows that the peak pressure increases rapidly with the increase of the radius and velocity,and the peak pressure has a linear relationship with the square of the radius of sphere and velocity.To calculate the distribution of the pressure coefficient along the surface of the sphere,we selected some test points in the sphere at different angles.The result shows the pressure coefficient has the maximum value when the test point touches water,and then decreases rapidly，and the pressure coefficient is sensative to the entry depth.

Keywords:sphere water entry； BEM； peak pressure； pressure coefficient

结构物入水是一个瞬态过程，在砰击入水过程中会受到巨大的冲击载荷，甚至会导致结构物的破坏，因此砰击问题的研究对于入水结构物的设计具有重要意义。如船舶在恶劣海况中航行的时候，由于船舶的剧烈起伏运动，首尾会频繁的入水，入水过程中所产生的砰击压力会造成船体结构的局部变形，严重的会造成船舶结构的破坏。随着海洋军事和民用航海领域的不断发展，砰击问题广泛存在于救生艇的落放、宇宙飞船的海上回收、海上飞机的降落，以及空投鱼雷入水等研究领域之中。入水砰击研究具有重要的工程应用背景。

砰击是一个十分复杂的物理现象，要涉及到固、液、气三种介质的耦合，理论分析比较困难，目前仍没有一种可以适合各种情况的理论模型。为了问题的研究，通常使用结构物入水模型作为力学模型来分析。自20世纪30年代以来，结构入水问题的研究取得了很大的进展。Von Karman[1]最早采用附加质量代替流体的作用分析入水冲击的问题，提出了附加质量方法来计算入水的冲击载荷，将水上飞机降落在水面过程理想为二维楔形体入水的过程，并使用动量守恒定理推导出了入水冲击载荷计算公式。Wagner[2]将Von Karman的方法理论化,同时考虑到物体入水时有液面升高的现象，提出了小斜升角模型的近似平板理论，为入水问题的研究提供了基础。在Wagner的研究中，引入了水波影响因子，利用伯努利方程算出了冲击压力在结构物湿表面上的分布情况，使理论更加适合实际问题。

近些年来，人们对于入水压力的问题还是以二维问题的方面进行研究。Wu[3]等提出了二维楔形体的迭代求解方法，并且利用了边界元方法，使用柯西积分对楔形体入水近似解进行了求解。但是在工程实际中使用的结构形式多样性，二维方法有一定的局限性，因此研究三维物体的数值算法对于工程应用具有很强的实用价值。Faltisen等[4]以非轴对称的船体模型入水为研究对象，基于边界元方法、发展了Wagner理论，研究了三维入水砰击的数值方法。Korobkin等[5-6]从逆推的Wagner问题及线性Wagner问题两方面出发研究了三维入水砰击理论，解决了流场流动、压力分布及流域形状三方面的问题。

针对三维物体入水问题，国内学者针对实际应用，陈震等[7]采用基于有限体积法的数值仿真方法对三维球鼻艏的入水砰击问题进行了研究。王珂等[8]采用数值仿真的方法研究了三维刚性回转体的入水问题，分析了不同回转角度的回转体的砰击压力峰值的变化规律，并研究了以一定初速度入水时，结构质量对砰击压力的影响。

基于三维边界元方法进行了球面体三维入水方面的研究，在数值上方面从三维模型出发，继承了Wagner的自由液面抬升理论，引入了浸深因子CW[9]以确定等效自由液面的高度，并考虑网格运动，将物体的入水过程分成若干时间步，一般根据入水速度及入水时长进行划分，而且还要和网格的垂向尺寸相协调，计算每一个时间步对应的湿网格中心点速度势，直到时间步长的全部结束。然后再根据每一时间步记录的数据进行后续的流场计算,实现对入水问题的求解。文中所使用的算法不同于以往的二维算法：首先，建立了实际的物面模型，并进行了网格划分，使网格数足够多，形成和实际结构物面极为相似的三维边界元模型；同时考虑了三向流场，在实际意义上更接近三维算法。

1 数值求解方法

1.1Wagner方法和自由液面的处理

问题的假设是二维物体或者三维轴对称体竖直落入半无界水域，入水模型被视为刚性结构，并且认为物体在落水的短时间内速度保持定常。在入水过程中，作用于模型上的流体惯性力占主导地位[10]，忽略流体黏性、表面张力、可压缩性、重力以及入水模型表面与流体间的气垫效应，并且认为流体是无旋的。Von Karman最早采用附加质量的方法计算物体入水的受力问题。物体表面的边界条件施加于流体自由表面的初始位置，通过引入线性化的伯努利方程，对自由面边界条件进行简化。这里在原始Wagner方法的基础上进行了改进，引入了边界元方法，考虑具体浸水物面，采用非线性伯努利方程对压力进行求解。

假设水是理想不可压缩的无旋流体。这样，流场速度势φ满足Laplace方程

在物面和无穷远处满足

式中：Vn是物面外法线n方向上(指向流场)的速度。

将湿物面划分为N个面元，可以得到离散化的方程组：

式中：aij是j面元对i面元的影响系数，σj为j面元上的分布源密度，其中aij为

通过式(3)和(4)便可以求解出各面元中心点处的分布源密度，进一步可得到个面元中心点的速度势

进一步可以求出各面元中心点处的诱导速度

忽略大气压力和重力影响，由Bernoulli方程可求得物面冲击压力

物体在流场中所受到的力为

图1 发展的Wagner方法Fig.1 Generalized Wagner method

在VonKarman的方法中，忽略了自由表面的升高，物面与水面的交线位于静水面，很容易通过物体入水的深度和物面形状得到。如图1所示，在Wagner方法中，自由表面条件应用在升高的自由表面上，也就是考虑了自由液面升高的影响。在笛卡尔坐标系o-xyz中，物体形状可以表示为Z=f(x,y)。如果t表示物体以速度V(t)入水的时间，则由于物体的运动导致物面形状方程为

t时刻自由液面的高度使用z=ζ(x,y,t)表示，在欧拉系统中满足dζ/dt=φz，所以点(x,y)处自由表面的升高为

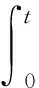
应注意到垂向速度φz是从升高的自由表面，而不是原静水面z=0。如果定义物面和自由水面的交界线为

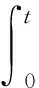
由式(9)和(10)得

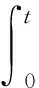
与Von-Karman的理论相比，可以看到湿表面和升高的自由水面是预先未知的。所以，它们的交界线，即物体的水线也是未知的。所有这些都需要求解后才知道。以上的过程也称为发展的Wagner方法。

文中所使用的算法在对自由液面进行线性化处理的时候，根据Wagner理论，考虑到了液面抬升。通常情况下，物体在入水过程中，自由液面与物体相交的位置均要高于原始的自由液面，流体有沿物面向上爬升的趋势，严格来说在计算的过程中必须要追踪自由液面的位置，这样才能使求解更加准确，但是对三维入水模型来讲，采用式(12)进行自由液面的追踪数值处理上还存在困难。例如文献[4]在三维船体入水砰击的自由液面追踪中，采用的方法是沿着船体与自由液面交界的一圈均匀标记若干点，之后分别以这些标记点为起点，平行于原始的自由液面画出射线，最终由作出的许多射线近似的拟合出一个抬升后的自由液面。本文算法也沿用了这种“射线延伸”的思想。采用线性化的自由液面，采用经验公式换算出物面与自由液面每一时刻的触点高度，以确定该触点的位置，并以之为起点平行于水平面的平面作为新的自由液面，即是“自由液面”。为了确定等效自由液面的位置，同时引入了浸深因子Cw=η/b。其中b=vt为物体的入水深度，η为自由液面升高加上b。

对于圆球体等轴对称钝体结构，Cw的取值如下：

其中，D是圆球的直径。

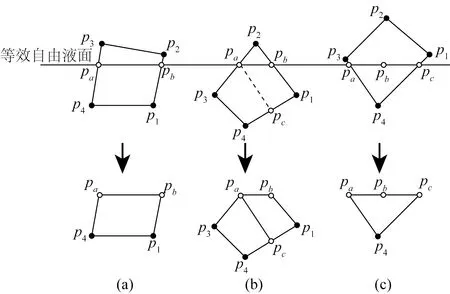
图2 自由液面处的网格处理方法Fig.2 Processing method for the grid at free surface

1.2网格入水过程中的处理

文中的计算程序是把三维边界元模型入水的时间历时分为若干个时间步进行了分析，在每一时间步时刻都要统计等效自由液面以下的面元以及节点的信息。但是在实际的计算模拟中，只有在水面下离等效自由面较远的网格能够保持完整性，在等效自由液面附近，沿着模型表面与等效自由面的交界线有一圈网格被自由液面所截断，生成新的面元网格；由于在程序中所使用的网格为长宽比值适中的四边形面元，并且为了提高程序的准确性，不能单纯的将这部分网格忽略，因此在程序中对于这部分网格进行了截断重生处理，如图2所示。

2 砰击载荷的数值计算结果与试验比较

为了研究高速物体结构入水过程中所受到的水动力压力大小，Adrian等[11]完成了一系列的入水受力测试试验，主要测试了若干铝合金制轴对称体以定常速竖直入水过程中的垂向受力数据，以供研究探讨。试验中所使用的模型如图3所示。

本文使用了三维边界元方法对文献[11]试验进行了数值模拟，并与模型实验的结果进行了对比。图4中T1为Wagner方法对应的半球体完全浸水时刻，通过球体模型的数值模拟可以发现，简化的半球体加密封盖模型在完全入水之前的压力历时和球体模型试验的结果吻合较好；在入水之后，由于半球缺少球体的一部分的表面积，所以在入水之后半球的总体受力迅速减小，与试验相比有误差。实际上，我们重点关注的是球体入水的最大冲击力，出现在球体入水的初期。所以，为了研究球体入水的峰值压力问题，采用了简化的半球体加密封盖模型，能够准确计算出半球体入水的最大受力，也是表面最大压力的大小和发生的时间。虽然T1之后的时段结构有偏差，但是这种情况下大大减少了计算量，提高了计算效率。

图3 试验中使用的模型Fig.3 Model utilized in the test

图4 半球以20 m/s速度入水垂向受力计算值与试验值比较Fig.4 Comparison of the pressures from calculation and model test(V =20 m/s)

3 数值模拟及结果分析

在验证了算法的正确性之后，使用Abaqus/CAE程序建立了相应的边界元模型分别建立了半径为0.5、0.6、0.8、1.0 m半球型边界元模型，半球纵深H=D/4，并进行了网格的划分和节点的提取，网格和节点数见表1所示。

表1 模型的网格划分Tab.1 Division of the model grid

图5 边界元模型Fig.5 Mesh of boundary elements

所建立的边界元模型的外表面为物体的湿表面，同时也是面元法线的正方向一侧。图5(a)是实际入水试件表面，在计算入水压力时，只考虑其表面上的压力值。在半球完全入水之前，参与计算的仅仅是其中的一部分面元，这样可以与抬升后的自由液面对称可得到一封闭的面元体结构，这样就可以根据面元法求解方程，进行面元源强的求解；随着时间的推移，当所有面元全部位于抬升后的自由液面以下时，这样与等效自由液面得到的面元体就不是闭合结构，不符合势流理论的求解原理，方程不成立。因此根据实际情况边界元模型加上了一个上盖，如图5(b)所示的结构。这样在图5(a)中面元完全入水之后，图5(a)和图5(b)共同组成了一个闭合的边界元模型，经与抬升后的自由液面对称便可以形成两个闭合的边界元模型。在计算的过程中，认为在半球入水之后液体立即将半球吞没。

为了研究球面上不同位置的表面压力分布，在计算的过程中针对性的选取了5个位置(图6)，计算了这些位置处的压力，并统计了压力峰值。在砰击试验中，物面各点的压力常用p=0.5CpρV2表示。其中Cp为无量纲冲击压力系数，反映物面各点的压力水平；ρ为流体密度；V指物体入水速度。采用无量纲的表示形式，还计算了半球入水过程中压力系数沿球体表面的分布情况，选取的测点如图6所示。这些点在下文中用其所在位置的径向射线与球体对称中心线之间的夹角表示。这些点的标号在图6中由左至右分别为：0°单元、10°单元、20°单元、30°单元和40°单元。

图6 半球体表面压力计算点分布Fig.6 Location of the points chosen for pressure calculation

图7给出了不同半径在不同速度下入水压力随时间的变化曲线，通过计算可以发现在球体在入水之后，压力迅速达到峰值，然后迅速回落。针对同一半径的球体，受力峰值对入水速度非常敏感。例如图7(c)，半径为0.8 m的球体在10 m/s时的受力峰值约为100 kN，而速度为20 m/s时受力的峰值约为400 kN。不同半径的球体以不同速度入水时的受力峰值见图8所示，其中横坐标用速度的平方表示。可见球体的峰值受力与入水速度的平方呈线性关系。针对不同的入水速度，受力峰值与半径的关系统计见图9所示，同样存在线性的比例关系。

图7 球体以不同速度入水时垂向受力的历时曲线Fig.7 Time history of vertical forces acting on the sphere at different entry speeds

图8 受力峰值随入水速度平方变化Fig.8 Peak force with t square of entry velocity

图9 受力峰值随半球半径平方变化Fig.9 Peak force with square of sphere radius

图10为半径1 m的球体在5个位置点的压力系数随时间的变化。因为球体入水过程中，0°单元先着水，依次是10°、20°、30°和40°单元。从时历变化可见，各点的压力在触水时刻达到最大值，然后呈级数形式下降。先触水的几点压力在初期的数毫秒内下降迅速，然后降速变缓。点的位置与球体中心线越接近，在入水时间内的压力水平越高。图11为不同半径的球体以20 m/s的速度入水时，0°单元上压力的时间变化。半径越大，其压力水平越高。

图10 半径1 m半球时压力系数(V=10 m/s)Fig.10 Time history of Cp at 10 m/s entry speed

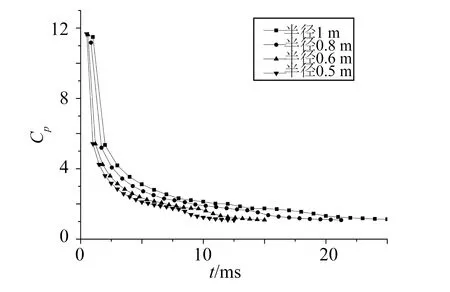
图11 不同半径球体0°面元压力系数(V =20 m/s)Fig.11 Time history of Cp on 0° element

半径为0.5 m的球体上的0°单元以不同速度入水时压力与入水深度之间的关系见图12所示。可以看出，不同的入水速度情况下，无量纲的压力系数几乎重合。说明对同一球体而言，只球体上各点的Cp与入水速度无关。而对于不同球体而言，综合考虑压力与浸入深度b和球体尺度r的关系，可以得到一个统一的压力系数，如图13所示。

图13 不同半径球体0°面元压力系数(V =20 m/s)Fig.13 Cp on 0° element of different spheres

4 结 语

以三维边界元方法编写了半球入水的砰击载荷计算程序，与轴对称体入水试验的结果进行对比，验证了程序的正确性，在此基础上可以对方法进行改进，对任意三维物体入水砰击载荷进行计算。

1)通过数值计算可以发现半球在入水的过程中，最大砰击力出现在入水初期，并在峰值出现后迅速减小；自由液面在入水初期对球体的影响较小，在球体入水的后期影响较大。

2)通过不同半径和不同速度的半球模型对比可以发现，入水的最大砰击力与半径的平方成正比例关系，与入水速度的平方成正比关系。

3)通过在球体表面选取的测试点压力系数的计算，结果表明压力系数在测试点和水接触时达到最大值；球体压力系数随着球体在水中的深度而变化，局部压力系数只取决于水中形状，和入水的速度无关。

[1] VON KARMAN T.The impact of seaplane floats during landing[R].Washington D C,USA:National Advisory Committee for Aeronautics,NACA Technical Notes 321,1929.

[2] WAGNER V H.Phenomena associated with impact s an d sliding on liquid surfaces[J].Z Angew Math Mech,1932,12(4):193-215.

[3] WU G X,SUN H,HE Y S.Numerical simulation and experimental study of water entry of a wedge in free fall motion[J].Journal of Fluids and Structures,2004,19:277-289.

[4] FALTINSEN O M,CHEZHIAN M .A generalized wagner method for three-dimensional slamming[J].Journal of Ship Research,2005,49(4):279-287.

[5] SCOLAN Y M,KOROBKIN A A.Three-dimensional theory of water impact:Part 1.inverse wagner problem[J].Journal of Fluid Mechanics,2001,440:293-326.

[6] KOROBKIN A A,SCOLAN Y M.Three-dimensional theory of water impact:Part 2.linearized wagner problem[J].Journal of Fluid Mechanics,2006,549:343-373.

[7] 陈震,肖熙.三维球鼻艏入水砰击研究[J].船舶工程,2007,29(4):61-64.(CHEN Zhen,XIAO Xi.Impacting study on the water entry of 3D bulbous bows[J].Ship Engineering,2007,29(4):61-64.(in Chinese))

[8] 王珂，陈刚，袁洪涛.三维回转体入水砰击载荷预报[J].船舶工程,2012,34(1):12-15.(WANG Ke,CHEN Gang,YUAN Hongtao.Prediction of the slamming pressure on a 3-D axisymmetric structure[J].Ship Engineering,2012,34(1):12-15.(in Chinese))

[9] JR A B W,MORRISON A M,BALDWIN J L.Prediction of impact pressures forces and moments during vertical and oblique water entry[M].1977:SWC/WOL/TR 77-16.

[10] FALTINSEN O M.Hydrodynamics of high-speed marine vehicles[M].New York:Cambridge University Press,2005:286-341.

[11] CONSTANTINESCU A,ALAOUI A E M,NEME A,et al.Numerical and experimental studies of simple geometries in slamming[J].International Journal of Offshore and Polar Engineering,2011,21(3):216-224.

Numerical calculation of slamming load for different curvature of the sphere

YU Longchao1,YAN Fasuo1,ZHAO Jiulong2,WANG Qi1

(1.Harbin Engineering University,Harbin 150001,China; 2.Hudong-Zhonghua Shipbuilding (Group) Co.,Ltd.,Shanghai 200129,China)

O353.4

A

10.16483/j.issn.1005-9865.2016.01.005

1005-9865(2016)01-0033-07

2015-01-08

于龙超(1990-)，男，河南鹿邑人，硕士生，主要从事海洋工程结构物设计分析。E-mail:yanfasuo@163.com