弯曲网格上的间断有限元湍流数值解法研究

秦望龙，吕宏强，伍贻兆

（南京航空航天大学 航空宇航学院，江苏 南京 210016）

弯曲网格上的间断有限元湍流数值解法研究

秦望龙，吕宏强，伍贻兆

（南京航空航天大学 航空宇航学院，江苏 南京 210016）

采用间断有限元方法对雷诺平均Navier-Stokes（RANS）方程进行了数值求解，对Spalart-Allmaras单方程湍流模型进行了部分修正，使得求解器更加鲁棒。构造了分段高次多项式来逼近真实物面，同时物面附近采用多层弯曲网格来避免网格交叉，此外提出了一种快速计算积分点的曲面物面距的方法。采用混合网格对NACA0012翼型以及RAE翼型进行了数值计算，并与实验数据以及前人数据进行了对比。计算结果表明，采用物面弯曲网格结合修正的湍流模型方法在相对稀疏的网格上就能得到比较好的数值解。

间断有限元；RANS；Spalart-Allmaras湍流模型；物面距；混合网格

0 引 言

近年来，随着众多学者的深入研究，间断Galerkin有限元（Discontinous Galerkin，DG）方法求解雷诺平均Navier-Stokes（Reynolds-averaged Navier-Stokes，RANS）方程取得了迅速发展［1-11］。目前采用DG方法求解RANS方程的湍流模型主要有一方程Spalart-Allmaras模型［4-10］、两方程Wilcoxk-ω模型［1-3］以及两方程剪切力运输（SST）模型［11］。

由于RANS方程本身的非光顺性质，间断有限元方法对其求解比较困难。尤其当采用稀疏网格，单元内会出现吉布斯（Gibbs）现象导致求解失败。针对SA一方程模型的稳定求解问题，一些学者提出了相应的方法［4-7］。文中采用一种修正的S-A一方程模型较好的抑制了Gibbs现象，顺利求解了RANS方程。

间断有限元方法对物面形状的表达精度非常敏感，如果物面采用分段线性网格进行计算会导致求解不收敛或数值结果不光顺［12-13］。为了解决以上问题，一般采用二次及以上多项式进行高阶近似以逼近真实物面，文献［14-18］给出了不同的高阶近似方法。然而在求解粘性流动，尤其是雷诺数较大时，由于第一层网格厚度很小，物面高阶近似会带来网格的交叉缠绕，从而出现负体积。为了使求解顺利进行，文中采用多层弯曲网格递推的方法，以很小的计算代价解决了以上问题。

Spalart-Allmaras单方程模型及SST两方程模型的求解需要计算积分点的物面距。对于弯曲物面，积分点的物面距的求解比较困难，Liu等人采用有限元方法对Eikonal方程进行数值离散求解了内流问题中的物面距［19］。然而，该方法在求解外流问题时会不稳定，Schoenawa采用流线-扩散方法对Eikonal方程进行离散求解，并引入人工粘性方法使其稳定鲁棒［11］。为了不额外引入计算方程，本文采用一种简单的数值方法对物面距进行计算。

1 控制方程

可压缩的雷诺平均Navier-Stokes方程耦合修正的一方程Spalart-Allmaras湍流模型可以写成如下的守恒形式：

其中，Ω是有界域。守恒变量u、无粘数值通量Fc、粘性数值通量Fv可以写成如下矢量形式：

其中，ρ、p、e0、h分别是密度、压强、单位总能和单位总焓，ui＝（vx，vy）是笛卡尔坐标系下的速度分量。压强p满足理想气体方程：

γ是定压比热容Cp与定容比热容Cv的比值，文中γ取1.4。σij是粘性应力张量，对于牛顿流体，

其中，μ是动力粘性系数，可以通过Sutherland公式得出。μT是湍流粘性系数：

湍流生成项和消散项中的参数分别如下：

2 数值方法

2.1 数值离散

将计算域表示成单元集合Ω＝∪kΩk，文中Ωk是四边形单元或三角形单元。定义Vh，p是单元h上采用多项式基函数表示的p阶有限元空间，p≥0。单元变量uh可以在Vh，p下表示，即uh∈Vh，p。对方程（1）离散，有

式（10）中，F（uh，∇uh）是对流通量和粘性通量的和。边界通量H=F（uh，∇uh）·n的求解需要引入合适的数值通量函数。文中采用LLF数值通量求解边界无粘数值通量［21］。对于粘性项，采用BR2格式（the second scheme of Bassi and Rebay）［1］进行数值离散。

2.2 时间积分

数值离散之后，方程最终可以写成一个常微分方程系统：

式（11）中，M是质量矩阵，R（Uh）是残值，Uh是未知变量。文中采用隐式向后欧拉方法对式（11）进行数值求解。每个迭代步产生一个线性方程组：

对于式（12）的求解文中采用ILU预处理的广义最小余量方法［22］。

3 网格弯曲处理

高阶间断有限元方法对物面形状的表达精度非常敏感，文中采用三次多项式对物面边进行分段高阶近似，从而逼近真实物面。求解高雷诺数粘性流动时，在物面进行高阶近似的同时需要对相邻外层网格进行高阶近似才能避免网格交叉缠绕。

区别于文献［18］中的映射方法，文中采用参数方程实现物面高阶近似和曲面网格阵推。如图1，将曲线AB表示成参数方程形式：

根据边界点A、B的坐标及加权方法算出的法矢nA、nB，可以求出上述方程的八个参数，从而实现物面弯曲。在此基础求出AB线段1／3、2／3点a、b处的弯曲距离α、β。根据每一层的阵推距离K1α、K2β以及边界点A1、B1，我们可以求出所有弯曲边的高阶参数方程形式。这里，K1、K2是调节因子，用于调节该面弯曲的程度，文中均取1．0。采用以上方法可以求出任意弯曲层数下弯曲边的表达形式，进一步提高了网格弯曲的自动化，并且为计算曲面物面距中搜索点的法矢提供了保证。需要指出的是，在实现高阶近似过程中，对于物面一些特殊点，如翼型后缘尖点，由于过该点的相邻边不是圆滑过渡，所以该点的法矢不能简单采用加权平均的方法进行计算，否则逼近的外形会偏离真实外形。

图1 网格单元高阶近似示意图Fig.1 Illustration of high order approximation

4 曲面物面距

为了不额外引入方程而准确计算积分点的曲面物面距，我们对物面边进行遍历，求出积分点到物面的最小距离d。

对于固定曲面物面，根据积分点的位置可以将其分为三类（图2），然后根据式（14）分别求解。

当积分点处于b情况时，对该曲面物面进行二分法遍历，直到在曲面上找到点g满足n（g）·l（bg）＝cosα＝0。n（g）表示曲面上g点的单位法矢，l（bg）表示b点到g点的单位向量，α是两向量的夹角。为了减少遍历次数，文中α取不小于80°。采用以上方法对RAE翼型的物面距的计算结果如图3，等势线显示范围为［0．001，0．5］。该算例计算了2695个网格单元中心点到物面的距离，其中1320个点需要计算case b情形。由于对α的设置，该算例case b情形的遍历次数基本在2次及以下。

图2 高斯积分点的分类Fig.2 Possible cases of Gaussian quadrature points

图3 RAE翼型的物面距分布Fig.3 Wall distance solution of RAE airfoil

5 数值结果与分析

采用上述高阶间断有限元方法结合物面弯曲混合网格单元对RANS方程进行数值求解。

5.1 NACA0012翼型算例

计算来流条件为Ma＝0.3，α＝0°，Re＝1．85×106。高雷诺数条件决定了第一层网格的厚度很薄，文中第一层网格取弦长的2×10-5，对应Y＋＝4。计算网格单元如图4，其中非结构网格单元由结构网格单元剖分而来。由于物面采用大长宽比结构网格单元，该算例计算网格总数控制在2592。

图4 NACA0012翼型计算网格Fig.4 Mesh around NACA0012 airfoil

图5给出了计算空间点的物面距的等势线，显示范围为［0．001，0．5］。

图5 NACA0012翼型的物面距分布Fig.5 Wall distance solution of NACA0012 airfoil

图6给出了本算例的马赫云图及湍流粘性系数云图，图7给出了本算例四阶精度的表面压力系数Cp分布及摩擦阻力系数Cf分布曲线。可以看出，Cp计算结果与实验结果吻合较好。由于Cf没有实验数据，这里我们采用Fluent软件在14000个单元上计算得到的Cf数据作为比较，可以看出曲线走势大致吻合。

图6 NACA0012翼型马赫云图及湍流粘性系数云图Fig.6 Mach contours and eddy viscosity contours of NACA0012 airfoil

图7 Cp和Cf分布曲线Fig.7 Cpand Cfdistribution of NACA0012 airfoil

5.2 RAE翼型算例

计算来流条件为Ma＝0.4，α＝2．79°，Re＝6．5×106。采用混合网格单元，总数为2695（图8）。计算精度从1阶（p＝0）到4阶（p＝3），为使p阶初值尽可能的靠近最终收敛解，采用p－1阶的收敛解作为其初值。图9给出了本算例p＝3时的马赫云图及湍流粘性系数云图。图10给出了本算例的表面压力系数Cp分布及摩擦阻力系数Cf分布曲线，计算结果与参考文献［8］的计算结果吻合较好。由于文中曲线数据均未采用任何光顺方法，所以在单元边界处会有局部不光滑现象。

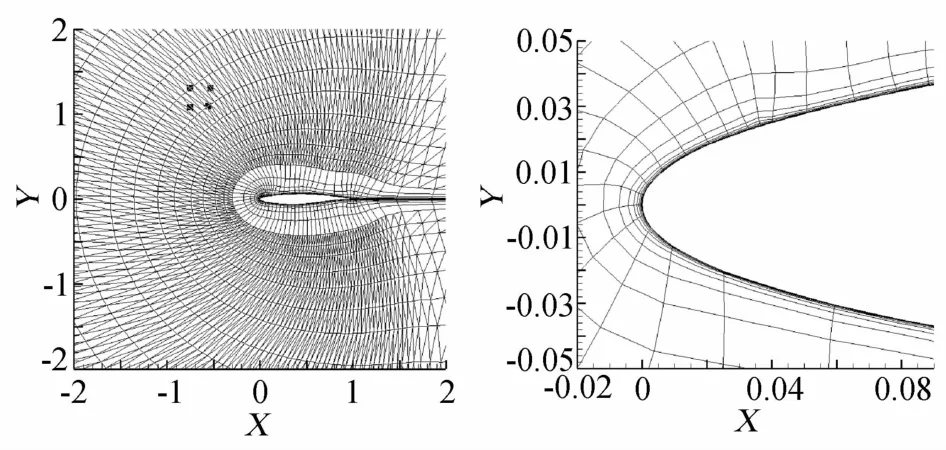
图8 RAE翼型计算网格Fig.8 Mesh around RAE airfoil

图9 RAE翼型马赫云图及湍流粘性系数云图Fig.9 Mach contours and eddy viscosity contours of RAE airfoil

图10 Cp和Cf分布曲线Fig.10 Cpand Cfdistribution of RAE airfoil

6 结 论

（1）采用高阶间断有限元方法对雷诺平均Navier-Stokes方程进行了数值离散和求解，湍流模型采用Spalart-Allmaras单方程湍流模型，并对其进行了部分修正，保证了数值求解的稳定性和鲁棒性。

（2）采用混合网格单元，物面采用参数方程实现高阶物面近似及曲面网格阵推，由于物面采用多层大长宽比弯曲结构网格单元，外部流场计算使用非结构网格单元，在较少的网格上就可以得到相当精度的数值解。

（3）给出了一种计算曲面物面距的方法，以很少的计算时间得到了满足计算需要的曲面物面距。

（4）采用以上方法对NACA0012翼型和RAE翼型高雷诺数算例进行了数值计算，验证了文中的物面距求解方法和湍流模型方法。

［1］BASSI F，CRIVELLINI A，REBAY S，et al．Discontinuous Galerkin solution of the Reynolds-averaged Navier-Stokes andkωturbulence model equations［J］．Computers&Fluids，2005，34（2）：507-540．

［2］BASSI F，CRIVELLINI A，GHIDONI A，et al．High-order discontinuous Galerkin discretization of transonic turbulent flows［C］．In Proceedings of the 47th Aerospace Sciences Meeting，Oriando；AIAA-2009-180．

［3］HARTMANN R，HELD J，LEICHT T．Adjoint-based error estimation and adaptive mesh refinement for the RANS andk-ω turbulence model equations［J］．Journal of Computational Physics，2011，230（11）：4268-4284．

［4］NGUYEN N C，PERSSON P O，PERAIRE J．RANS solutions using high order discontinuous Galerkin methods［C］．The 45th Aerospace Sciences Meeting，Reno，2007；AIAA-2007-914．

［5］OLIVER T，DARMOFAL D．An unsteady adaptation algorithm for discontinuous Galerkin discretizations of the RANS equations［C］．The 18th AIAA Computational Fluid Dynamics Conference，Miami，2007；AIAA-2007-3940．

［6］LANDMANN B，KESSLER M，WAGNER S，et al．A parallel，high-order discontinuous Galerkin codes for laminar and turbulent flows［J］．Computers&Fluids，2008，37（2）：427-438．

［7］MORO D，NGUYEN N C，PERAIRE J．Navier-Stokes solution using hybridizable discontinuous Galerkin methods［C］．The 20th Computational Fluid Dynamics Conference，Honolulu，2011；AIAA-2011-3407．

［8］BURGESS N K，MAVRIPLIS D J．Robust computation of turbulent flows using a discontinuous Galerkin method［C］．The 50th Aerospace Sciences Meeting，Nashville，2012；AIAA-2012-0457．

［9］BURGESS N K，MAVRIPLIS D J．High-Order Discontinuous Galerkin Methods for Turbulent High-lift Flows［C］．The 7th International Conference on Computational Fluid Dynamics（ICCFD7），Big Island，2012，ICCFD7-4202．

［10］WANG L，ANDERSON W K，ERWIN J T，et al．Solutions of high-order methods for three-dimensional compressible viscous flows［C］．The 42nd AIAA Fluid Dynamics Conference and Exhibit，New Orleans，2012．

［11］SCHOENAWA S，HARTMANN R．Discontinuous Galerkin discretization of the Reynolds-averaged Navier-Stokes equations with the shear-stress transport model［J］．Journal of Computational Physics，2014．

［12］LÜH Q，WU Y Z，ZHOU C H，et al．High resolution of subsonic flows on coarse grids［J］．Acta Aeronautica et Astronautica Sinca，2009，30（2）：200-204（in Chinese）．

吕宏强，伍贻兆，周春华等．稀疏非结构网格上的亚音速流高精度数值模拟［J］．航空学报，2009，30（2）：200-204．

［13］LU H．High-order discontinuous Galerkin solution of low-Re viscous flows［J］．Modern Physics Letters B，2009，23（03）：309-312．

［14］LÜBON C，et al．High-order boundary discretization for discontinuous Galerkin codes［C］．In Proceedings of the 24th Applied Aerodynamics Conference，Francisco，2006；AIAA-2006-2822．

［15］HARTMANN R，HELD J，LEICHT T，et al．Discontinuous Galerkin methods for computational aerodynamics－3D adaptive flow simulation with the DLR PADGE code［J］．Aerospace Science and Technology，2010，14（7）：512-519．

［16］PERSSON P，PERAIRE J．Curved mesh generation and mesh refinement using Lagrangian solid mechanics［C］．In Proceedings of the 47th Aerospace Sciences Meeting，Oriando，2009；AIAA-2009-949．

［17］YU J，YAN C．Study on discontinuous Galerkin method for Navier-Stokes equations［J］．Chinese Journal of Theoretical and Applied Mechanics，2010，42（5）：962-969（in Chinese）

于剑，阎超．Navier-Stokes方程间断Galerkin有限元方法研究［J］．力学学报，2010，42（5）：962-969．

［18］QIN W L，LÜH Q，WU Y Z．High-order discontinuous Galerkin solution of N-S equations on hybrid mesh［J］．Chinese Journal of Theoretical and Applied Mechani.，2013，45（6）：987-991．（in Chinese）

秦望龙，吕宏强，伍贻兆．基于混合网格的高阶间断有限元黏流数值解法［J］．力学学报，2013，45（6）：987-991．

［19］LIU C B，NITHIARASU P，TUCKER P G．Wall distance calculation using the Eikonal／Hamilton-Jacobi equations on unstructured meshes：a finite element approach［J］．Engineering Computations，2010，27（5）：645-657．

［20］SPALART P，ALLMARASS．A one-equation turbulence model for aerodynamic flows［C］．In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit，Reno，1992；AIAA-92-0439．

［21］XIA Y D，WU Y Z，LÜH Q，et al．Parallel computation of a high-order discontinuous galerkin method on unstructured grids［J］．ACTA Aerodynamica Sinica，2011，29（5）：537-541．（in Chinese）

夏轶栋，伍贻兆，吕宏强，等．高阶间断有限元法的并行计算研究［J］．空气动力学学报，2011，29（5）：537-541．

［22］SAAD Y，SCHULTZ M H．GMRES：A generalized minimal residual algorithm for solving nonsymmetric linear systems［J］．SIAM Journal on Scientific and Statistical Computing，1986，7（3）：856-869．

Discontinuous Galerkin solution of RAN Sequations on curved mesh

QIN Wanglong，LÜ Hongqiang，WU Yizhao
（College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

Discontinuous Galerkin（DG）finite element method was adopted for the numerical approximation of the Reynolds-averaged Navier-Stokes（RANS）equations with the Spalart-Allmaras turbulence model．In order to make the solver robust，the original turbulence model equation were modified accordingly．Furthermore，high order approximation of the real solid boundary was used and several layers of curved meshes were constructed to avoid inconsistent mesh cross-overs．For the computation of the distance of each quadrature point to the nearest curved wall boundaries，a fast straightforward numerical method was proposed．The DG discretization of the RANS equations were demonstrated for turbulent flows past a NACA0012 airfoil and RAE airfoil based on hybrid mesh．Numerical results indicate that highly accurate solutions can be obtained with the modified turbulent equation on coarse curved hybrid mesh．

Discontinuous Galerkin（DG）；RANS；Spalart-Allmaras turbulent model；high order approximation；hybrid mesh

V211.3

Adoi:10.7638／kqdlxxb-2014.0058

0258-1825（2014）05-0581-06

2014-06-24；

2014-08-10

国家自然科学基金（11272152）；航空科学基金（20101552018）；江苏高校优势学科建设工程资助项目

秦望龙（1988-），男，江苏南通人，博士研究生，主要研究方向：计算流体力学，高阶间断有限元．E-mail：qinwanglong＠126．com

吕宏强，博士，副教授．E-mail：hongqiang．lu＠126．com

秦望龙，吕宏强，伍贻兆．弯曲网格上的间断有限元湍流数值解法研究［J］．空气动力学学报，2014，32（5）：581-586．

10．7638／kqdlxxb-2014．0058． QIN W L，LU H Q，WU Y Z．Discontinuous Galerkin solution of RAN Sequations on curved mesh［J］．ACTA Aerodynamica Sinica，2014，32（5）：581-586．