钢悬链式立管与非线性海床土相互作用分析方法研究
2016-10-12黄维平杨超凡
梁 宁,黄维平,杨超凡
(中国海洋大学 山东省海洋工程重点实验室,山东 青岛 266100)
钢悬链式立管与非线性海床土相互作用分析方法研究
梁 宁,黄维平,杨超凡
(中国海洋大学 山东省海洋工程重点实验室,山东 青岛 266100)
对基于大挠度柔性梁理论的立管动力分析程序CABLE 3D改编,将原程序中立管受到线性海床的弹性支撑力扩充为立管受到的海床垂向力充分考虑管土非线性相互作用,使新程序中立管与海床土的相互作用遵循p-y曲线。采用伽辽金方法在空间内离散立管的动态方程,最终采用Newmark-β法进行时域内迭代求解。利用改编后的新程序分别研究了立管与线性海床土和非线性海床土相互作用的对比以及不同垂荡幅值情况下立管的动态响应。研究表明,非线性海床土能够更加准确地模拟真实的管土相互作用,触地点区域的节点会经历不同的管土相互作用过程。
管土相互作用;钢悬链式立管;非线性海床土;动态响应
Abstract:The riser dynamic analysis program CABLE 3D is reprogramed based on the theory of the flexible beam with large deflection.The original program in which the riser has linear elastic seabed support is adapted to the riser under the seabed vertical force fully considering nonlinear interaction of pipe and soil.The new program’s interaction of riser with seabed follows thep-ycurves in this paper.Galerkin method is used in space discrete dynamic equation,and finally time domain iterates after discrete equation by the method of Newmark-β.The interaction of the riser with linear and nonlinear seabed soil is studied,and the steel catenary riser’s dynamic response in different cases of heaving amplitude is analyzed by using the new program after adaptation.The results show that the nonlinear seabed soil can be used to simulate a more accurate interaction between riser and soil,and the nodes at the touch-down zone of the riser may undergo different processes of the interaction.
Keywords:interaction between risers and seabed; steel catenary riser; nonlinear seabed; dynamic response
随着海洋油气资源开发逐步深入,复杂的海洋环境对立管系统的要求也随之增高[1]。钢悬链式立管(SCR)集海底管线和立管与一身,一端连接海底井口,另一端通过柔性接头连接浮式结构[2]。钢悬链式立管是一种自由悬挂的立管形式,其与海床刚接触的区域称为触地点区域。触地点区域是研究、分析的重点位置。为了能够准确地分析立管触地点处响应,需要采用合理的海床土模型[3]。
管土相互作用是一个包含着立管、海床与海水的非常复杂的作用过程。海床土对钢悬链式立管的主要影响因素包括两个方面:1)钢悬链式立管向着海底运动时,海床刚度的作用;2)钢悬链式立管作拔出海底运动时,海床土体吸力的作用[4]。
Bridge等[5]进行了大尺度的立管模型实验,研究提出了海床动刚度和土吸力模型;You[6]提出了简化的弹簧支撑模型,将海床对SCR的支撑作用简化为有限数量的弹簧支撑;Aubeny等[7]提出了描述海床土刚度的p-y曲线和等价梁-弹簧模型;白兴兰[4]采用具有弯曲刚度的大挠度细长梁模拟钢悬链线立管,研究了立管与海床法向相互作用中立管管向着海床运动时海床刚度的影响和立管拔出海底时的吸力作用。
选用非线性p-y曲线来模拟钢悬链式立管与海床土的相互作用。p代表海床土的支撑力而y代表立管贯入海床土的深度。对基于大挠度柔性梁理论的立管的动力分析程序CABLE 3D进行改编,将原程序中立管受到线性海床的弹性支撑力扩充为立管受到的海床垂向力考虑管土非线性相互作用,从而使新程序中立管与海床土的相互作用遵循p-y曲线。利用改编后的新程序分别研究了立管与线性海床土和非线性海床土相互作用的对比以及不同垂荡幅值情况下SCR的动态响应。
1 SCR的大挠度细长梁模型
1.1SCR的控制方程
在三维笛卡尔坐标系中,杆的瞬时形态可以用一个向量r(s,t)表示,这个向量是沿着杆长弧长s和时间t的函数(见图1)。其中t,n和b分别是切线、法线和次法线方向的单位向量,而ex(e1),ey(e2)和ez(e3)分别是x,y和z轴的单位向量。
其中,q是单位长度的外部分布力,ρ是单位长度质量,m是单位长度的外部弯矩。在不能伸长条件的假设下可以推导出运动方程:
其中,H是扭矩,B是弯曲刚度,κ为杆的局部曲率,T是局部张力。在小变形条件下可推导出:
其中,ε=T/(EA),EA是杆的弹性刚度。最终可获得控制方程:
其中,ρf为海水质量密度;ρi为内部流体质量密度;ρt为管子的质量密度;Af为杆外部截面积;Df为杆直径;Ai为杆内部截面积;At为杆实际结构截面积;vf为海水的速度(流和浪);af为海水的加速度(流和浪);Pf为海水的压力;Pi为内部液体的压力;T,N为转化矩阵;I为单位矩阵。
1.2数值求解
1.2.1 有限元模型
小伸长杆的运动方程和约束条件可以改写为:
1.2.2 静态问题
静态问题中所有对时间求导项都设定为零。采用牛顿方法,对小伸长单元静态问题可得到以下方程:
对于每一个单元都将方程(12)和(13)写成矩阵aδx=b的形式,其中未知矢量δx包含15个未知量。在第一个单元和最后一个单元的自由端施加边界条件。采用高斯消去法对最终方程aδx=b进行求解。
1.2.3 时间积分
采用Newmark-方法[8]求解非线性微分动态方程。在t=0,或者时间步K=0时:

最终得:
2 管土相互作用模型
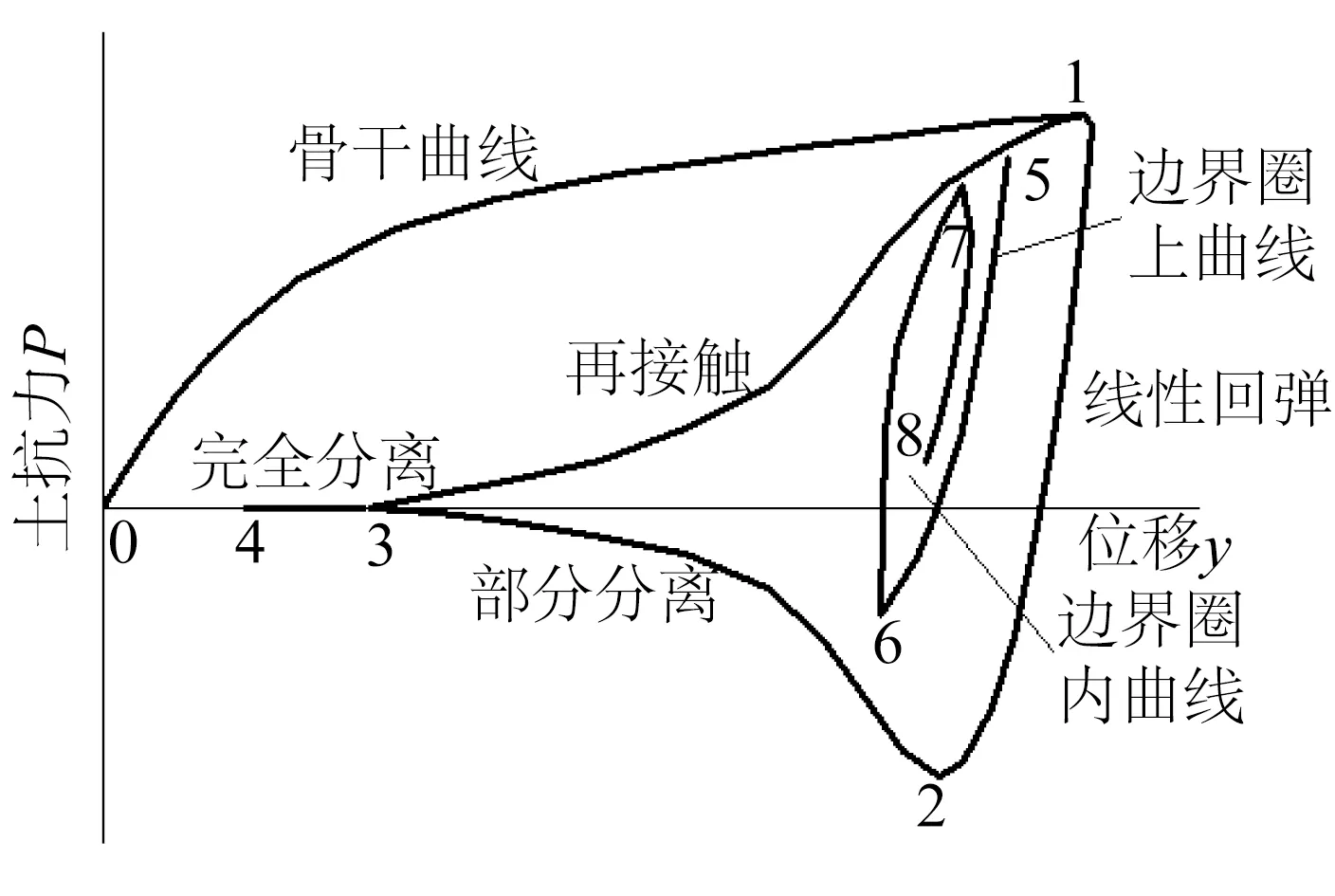
图2 管土相互作用曲线p-y曲线Fig.2 p-y curve of the riser-soil interaction
钢悬链式立管与海床土的相互作用呈现显著的非线性特征。其受到立管直径、海床土的不排水抗剪强度、沟槽形成的宽度与深度、海床土吸力等因素的影响[9]。如图2所示,采用的p-y曲线包括骨干曲线、管土完全接触的弹性回弹曲线、管土部分分离曲线、完全分离阶段和再接触阶段,以及在边界圈上和边界圈内部的管土作用曲线。
2.1骨干曲线模型
骨干曲线对应由于立管自重的初始贯入,以及当立管向下运动达到之前的沟槽深度后又发生的贯入阶段,如图2中0-1段。骨干曲线定义了海床的最大压缩抗力是如何随着立管位移变化的,通过承载力理论确定的[10]。最终的骨干曲线的经验公式为:
其中,Su0是泥面处的剪切强度;Sg为对应立管深度z处的强度梯度;d为立管直径;a和b是曲线系数,其值根据表1进行选取,文中a和b是沟槽宽度与立管直径之比为一时的取值。

表1 a、b系数的取值Tab.1 The coefficient values of a and b
2.2边界圈的公式
采用Aubeny提出的模型来定义边界圈[11]。边界圈的几何特征由三个关键点确定。点1(y1,P1)为周期荷载作用下的初始点,点2(y2,P2)为吸力最大值点,点3(y3,P3)为立管和土壤完全分离的点。点1(y1,P1)等于在最大塑性贯入位移y1时对应的土壤作用力:
在上举运动中最大的吸力与最大的支撑力之间的关系为P2=-ΦP1,Φ为吸力极限系数。点3是用完全接触阶段的位移段长度与分离阶段位移段长度之间的关系确定。
此时P3等于零,ψ定义为土体和立管分离参数。在点1和点2之间的弹性回弹曲线用双曲型曲线表示:
式中:ω为吸力极限系数,根据试验数据和现场数据确定的。参数ω是控制双曲线渐近线的参数,同时和参数Φ一同控制开始发生分离时的位移y2。
式中:k0是双曲型曲线最初的斜率,该参数和土壤的未排水弹性模量Eu有一定的关系,即k0≈2.5Eu。在点2和3之间的部分分离阶段的曲线采用三次曲线模拟:
当管土完全分离后,SCR如果再次向下运动,那么立管会再次与土壤接触,土壤弹簧会恢复支撑力直至立管最终回到初始自重贯入深度,即从点3回到点1。这个再接触再加载阶段定义为上边界曲线:
2.3在边界圈内的逆向曲线模型
在边界圈内任意一点都可能发生逆向路径。因为加载路径非常复杂,所以提出了几个不同的模型方程来描述在不同情况下的卸载或加载曲线。在边界圈上任意一点(yrB,PrB),无论是从点1到点2之间发生逆转(即再加载)还是从点3到点1发生逆转(即卸载),都遵循从逆转点开始的双曲型的路径:
其中,χ是位移加载方向系数,对于卸载χ=-1,对于加载χ=1。而对于在边界圈内的任意一点(yr,Pr)发生逆转时,逆转曲线的方程如下:
对于在边界圈上,从部分分离区域即点2和点3之间发生的逆转曲线,应该遵循下面的三次曲线形式:
综上可以看出该p-y曲线充分考虑了SCR与海床相互作用的各个阶段以及各种情况,同时也能够考虑不同海域的土壤条件,能够更加真实地模拟管土相互作用。在后续数值计算也是基于该曲线展开。
2.4管土相互作用的求解
钢悬链式立管细长梁模型的运动方程和约束条件分别为式(8)和(9)。SCR与海床土的相互作用通过p-y曲线进行模拟。将各个分段的土壤刚度值统称为k,从而海床法向约束力可表示为:
对于与海床接触的SCR立管单元,将海床法向约束力作为一附加项放入SCR的运动方程(8)中得到:
再将方程代入增量形式的运动方程中即可进行求解。对控制方程和边界条件采用非线性有限元进行离散,在时域内采用Newmark方法求解,以此求解钢悬链式立管在不同时刻的响应。
3 算例分析
选择与某半潜平台相连接的钢悬链式立管在不同海床土情况下进行对比分析。钢悬链式立管外径为0.355 6 m,内径为0.304 8 m。SCR材料为钢材,弹性模量为2.07×108kPa,密度为7 850 kg/m3。工作水深为1 100 m。以SCR上端为原点(0,0,0),另一端坐标为(1 800,0,-1 100)。海底为平坦海床,海床表面处土壤强度选择低强度、中等强度和高强度三种情况,具体参数如表2所示。

表2 土壤参数Tab.2 Parameters of soil
3.1海床土非线性刚度与线性刚度对比
原CABLE 3D程序中采用的是线性刚度的海床土,海床土的刚度仅与SCR的直径与SCR单位长度的湿重有关。这里改编后的新程序采用p-y曲线模拟海床土的刚度,充分考虑了海床土在不同阶段的刚度变化。将SCR上端垂荡幅值设定为2 m,分别采用原程序和改编后新程序对SCR进行分析,并对其结果进行对比。其中,两者的分析时长皆为3 700 s。
3.1.1 最大贯入深度与触地点区域SCR形态
表3给出了程序计算得到的SCR在分析时长中SCR最大的贯入深度。其中贯入深度是以水平面为0点,SCR最外侧达到的最大深度。可知非线性土壤刚度情况下,得到的分析结果普遍比线性土壤刚度的分析结果小。采用线性土壤刚度相当于海床土的刚度非常低,从而使得SCR的贯入深度比较大。图3给出了在最大贯入深度对应时间步时的触地点区域的立管位形。可以看出当垂荡幅值2 m时,低强度海床土是分析的三种情况中最大贯入深度与线性海床土结果最为相近的,所以本节后续的对比分析选用低强度海床土与线性土壤对比。

表3 SCR最大贯入深度Tab.3 Maximum penetration depth of SCR
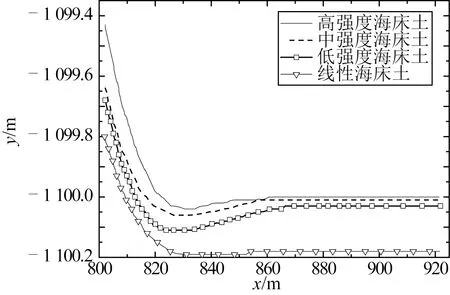
图3 SCR位形图Fig.3 The position and shape of SCR
3.1.2 最大贯入深度节点垂向位移对比
图4~5给出了分析时间为500 s到800 s中线性土壤和非线性低强度土壤情况下,最大贯入深度节点处SCR垂向位移响应时程图和频谱图。
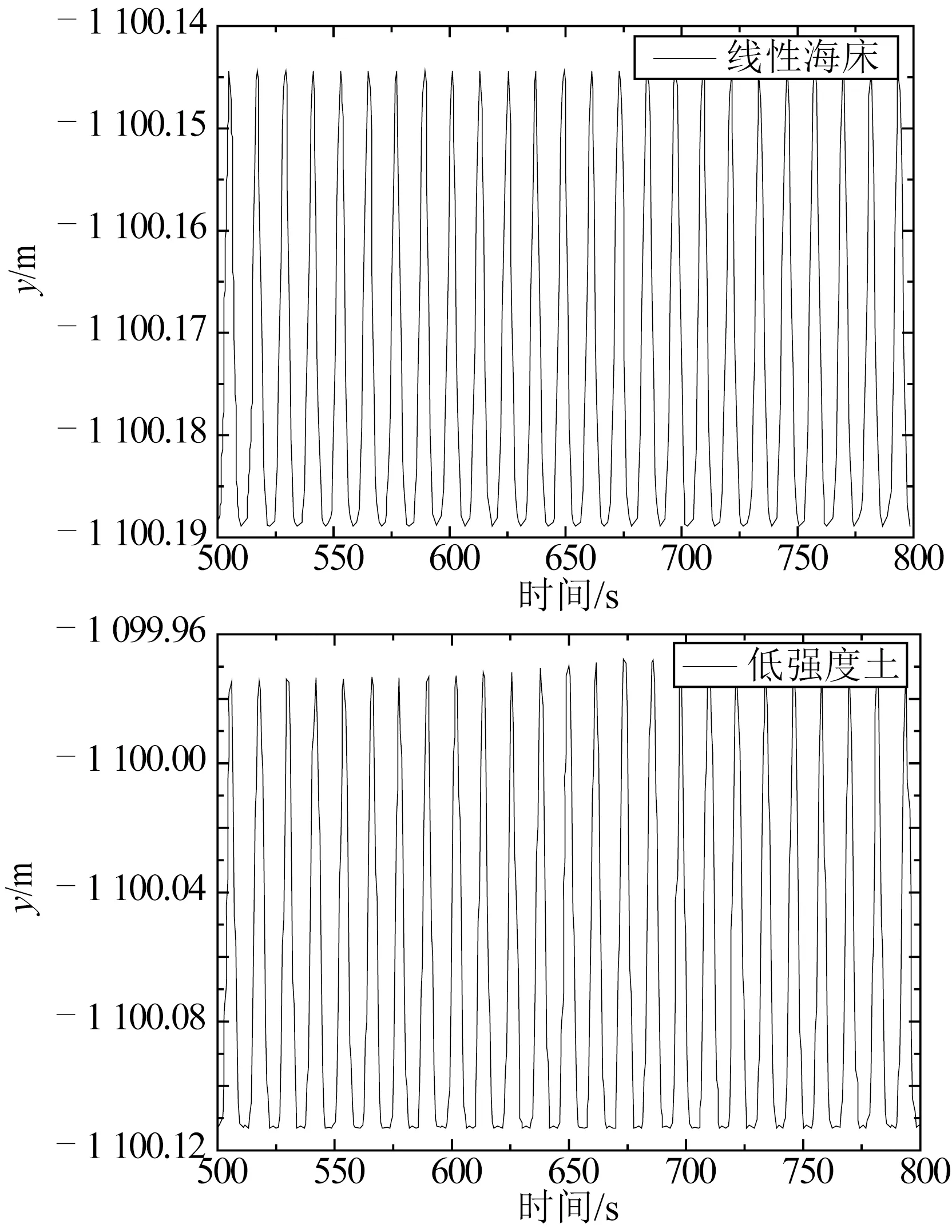
图4 位移响应时程图Fig.4 Displacement response in time domain

图5 线性土壤位移响应频谱图Fig.5 Displacement response in frequency domain
从图4中可以看出,线性土壤下SCR该节点的垂向位移响应呈现明显周期性,且幅值变化不大,垂向位移响应稳定在[-1 100.19,-1 100.145]之间(以海平面为z轴零点),幅值约为0.045 m。在非线性低强度土壤的情况下,SCR在该节点的垂向位移响应呈现明显周期性,幅值略有变化,垂向位移响应在[-1 100.12,-1 099.97]之间,幅值约为0.05 m。从图5中可以看出,线性土壤和非线性低强度土壤情况下,SCR的振动频率为0.083 Hz和0.166 Hz,其中前者恰为垂向运动的频率。因此,得出SCR的运动频率主要是受到外荷载的振动频率的影响,与海床土的性质关系不大。
3.1.3 海床土垂向约束力分析
图6给出了非线性海床分析中SCR触地点处三个不同节点在1 000~1 500 s时的荷载位移响应曲线。其中244节点为最大贯入深度对应的节点。从图中可以看出244节点和245节点都是经历了完整的卸载—管土部分分离—管土完全分离—再加载过程,并且在整个过程中是按照程序设定的p-y曲线的路径进行的。而246节点,是经历了卸载—再加载过程,但是该节点处SCR并没有与土壤发生分离,从而没有受到海床土的吸力作用。这也说明了在触底点区域并不是所有的SCR节点都会经历完全相同的管土相互作用过程。某一个时刻不同位置处的SCR受到不同的海底约束力,经历不同的非线性管土相互作用过程。
3.2上部结构运动对管土作用的影响
选用非线性低强度海床,上部结构垂荡幅值为1 m,2 m和3 m,周期皆为12 s,对钢悬链式立管进行分析。通过对比不同垂荡幅值下,SCR的最大贯入深度、触地点处SCR的位移时程图、SCR的弯矩值和应力值来分析上部结构的运动对SCR性能的影响。
3.2.1 最大贯入深度与触地点区域SCR形态
表4给出改编后程序计算得到不同垂荡幅值情况下钢悬链式立管在分析时长中最大的贯入深度。图7给出了在最大贯入深度对应的时间步时的触地点区域的SCR位形。该位形图结果与表3的结果一致,垂荡幅值越大,SCR在触地点区域的位置越靠下。由此可知,当海床土的强度确定时,上部结构的运动幅值越大,SCR的贯入深度越大。

表4 SCR最大贯入深度Tab.4 Maximum penetration depth of SCR
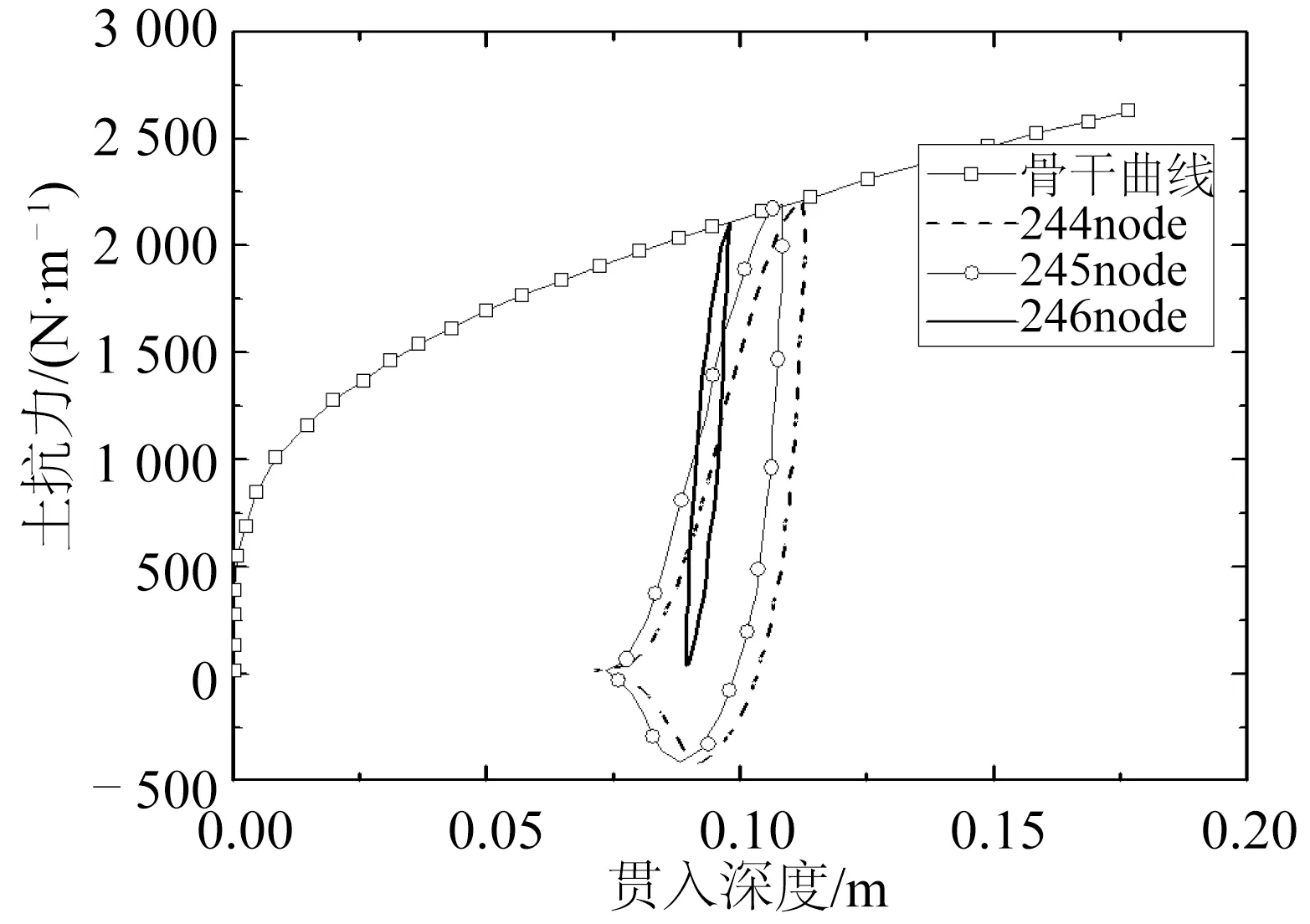
图6 低强度非线性海床p-y曲线Fig.6 p-y curves of nonlinear low intensity soil

图7 SCR位形图Fig.7 The position and shape of SCR
3.2.2 最大贯入深度节点垂向位移对比
图8~9给出了分析时间为500 s到800 s时间历程中垂荡幅值分别为1 m,2 m和3 m情况下对应的最大贯入深度节点处SCR垂向位移响应时程图和频谱图。从图8中可以看出不同垂荡幅值情况下,SCR的垂向位移响应皆呈现出明显的周期性,且幅值变化不大。随着垂荡幅值增大,垂向位移响应幅值分别约为0.003、0.15和0.31 m。当垂荡幅值为1 m时,仅激发了触地点处立管的一阶振动频率,为0.083 Hz。但是当垂荡幅值增加到2 m和3 m时,立管的振动幅值为0.083 Hz和0.166 Hz,其中前者恰为上部结构垂向运动的频率。因此,可以得出立管的运动频率主要是受到上部结构的振动频率的影响。

图8 垂荡位移响应时程图Fig.8 Displacement response in time domain

图9 垂荡位移响应频谱图Fig.9 Displacement response in frequency domain
3.2.3 弯矩、张力与应力
表5给出了不同强度海床土的弯矩最大值、弯矩最大幅值及其位置,最大应力值、最大应力幅值及位置。其中位置是指从SCR上端开始沿SCR轴向的距离。可以看出最大弯矩值明显受到上部结构运动情况的影响,上部结构运动幅值越大导致的最大弯矩值及最大弯矩幅值也就越大。应力值会随着弯矩值的增大而增大,也就是说最大应力值及应力幅值同样是明显受到上部结构运动情况的影响,上部结构的运动幅值越大,最大应力值及应力幅值也就越大。
图10给出了240~250 s中的一个弯矩幅值的波峰时刻不同垂荡幅值情况下沿管长的弯矩变化图。结合表5可以看出弯矩值最大值发生在触地点区域附近曲率变化剧烈的区域,但是弯矩值的幅值则是在触地点区域达到最大值,并且最大值出现的位置与上部结构运动幅值相关性不大。图11给出了张力沿SCR管长的变化。可以看出不同幅值情况下,SCR的张力都是沿着管长逐渐减小的,之后当SCR与海床土开始接触之后,张力的减小速率开始减慢。图12给出了应力沿SCR管长的变化。从图中可以看出应力沿着管长在上部区域和触地点区域的应力值最大。这是因为顶端的张力值最大,而触底点区域附近的弯矩值最大。结合表5可以看出应力值最大值发生在触地点区域附近曲率变化剧烈的区域,但是应力值的幅值则是在触地点区域达到最大值,并且在不同幅值时出现的位置基本相同,只是大小不同,这与弯矩值的变化呈现相同的规律。
综上所述,海床土的强度不变时,当上部结构的运动幅值增大时,此时相同立管情况下,最大的贯入深度越来越大;最大弯矩值和应力值都发生在触地点区域附近的曲率变化较大的位置,而最大的弯矩幅值和应力幅值发生在触地区域,且位置变化不大;最大弯矩值和最大应力值,以及弯矩幅度和应力幅值随着上部结构的垂荡幅值增大,而越来越大。
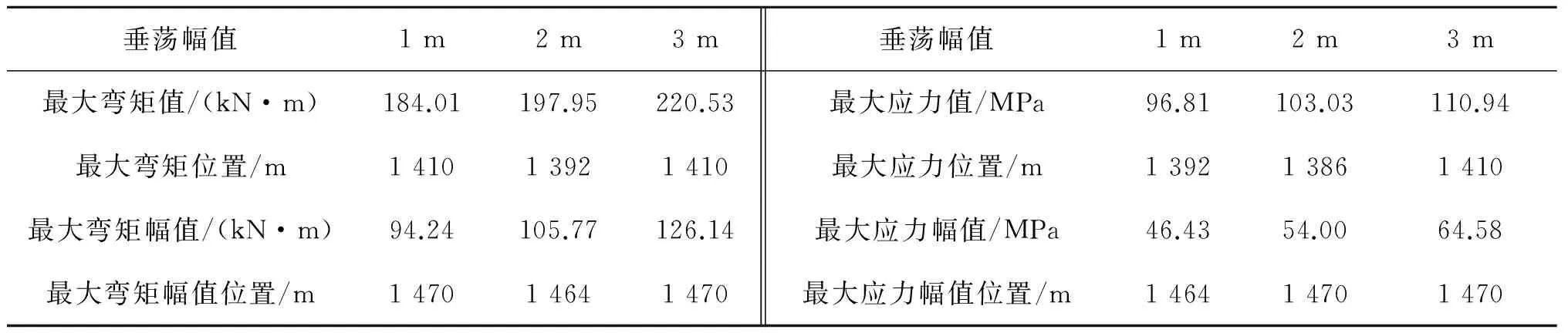
表5 弯矩值和应力值Tab.5 Bending moment and stress of SCR

图10 弯矩沿管长的变化Fig.10 Bending moment variation of SCR

图11 张力沿管长的变化Fig.11 Effective tention variation of SCR
4 结 语
采用大挠度细长梁模型模拟钢悬链式立管的运动,同时采用弹性基础梁模型模拟海床,而创新地用非线性p-y曲线模拟管土相互作用过程。该p-y曲线包括骨干曲线、管土完全接触的弹性回弹曲线、管土部分分离曲线、完全分离阶段和再接触阶段,以及在边界圈上和边界圈内部的管土作用曲线。在现有CABLE 3D程序基础上进行了改编,使新程序中SCR运动方程中海床土法向约束力遵循选用的p-y曲线。这样将非线性p-y曲线引入管土相互作用使得模拟更为准确。
算例中分别选取了海床土强度为低强度、中等强度和高强度三种情况,上部结构的运动情况只考虑垂荡值为1、2和3 m,周期都为12 s。计算了采用线性刚度土壤,在垂荡幅值为2 m时的立管响应,并与非线性土壤刚度情况进行对比。随后研究不同垂荡幅值情况下立管的动态响应。
结果表明,非线性管土相互作用能够更加准确的模拟真实的管土相互作用,非线性低强度海床土与原程序中线性海床土计算结果最为相近。在非线性管土相互作用分析过程中,触地点区域的节点会经历不同的管土相互作用过程。随着上部结构的运动幅值增加,立管的最大贯入深度也会相应的增加。立管最大弯矩值和最大应力值受到上部结构运动幅值的影响作用明显。因此,在立管设计过程中,针对上部结构的运动情况和不同的海床土参数,选取合理的设计参数对模拟立管与海床土的相互作用有重要参考意义。
[1] 梁辉.深水开发中的SCR立管系统[J].中国造船,2008,49(2):80-85.(LIANG Hui.Steel catenary risers in deepwater[J].Shipbuilding of China,2008,49(2):80-85.(in Chinese))
[2] 黄维平,李华军.深水开发的新型立管系统——钢悬链线立管(SCR)[J].中国海洋大学学报,2006,36(5):775-780.(HUANG Weiping,LI Huajun.A new type of deepwater riser in offshore oil& gas production:the steel catenary riser,scr[J].Periodical of Ocean University of China,2006,36(5):775-780.(in Chinese))
[3] BRIDGE C,LABER K,CLUKEY E,et al.Steel catenary riser touchdown point vertical interaction models [C]//Proceedings of the Offshore Technology Conference.2004:1-9.
[4] 白兴兰.基于惯性耦合的深水钢悬链线立管非线性分析方法研究[D].青岛:中国海洋大学,2009.(BAI Xinglan.Study on method for nonlinear analysis of deepwater SCR based on inertial coupling[D].Qingdao:Ocean University of China,2009.(in Chinese))
[5] BRIDGE C,WILLIS N.Steel catenary risers results and conclusions from large scale simulations of seabed interaction[C]//Proceedings of the 14th Annual Conference Deep Offshore Technology.2002.
[6] YOU J H.Numerical model for steel catenary riser on sea floor support[D].Texas:Texas A&M University,2005.
[7] AUBENY C P,BISCONTIN G,ZHANG J.Sea floor interaction with steel catenary risers[R].Texas:Texas A&M University,2006.
[8] ARGYRIS J,MLEJNEK H P.Dynamics of structures[M].New York:Elsevier Science Publication Co.,1991.
[9] 孟庆飞,黄维平.钢悬链线立管与海底相互作用弹性基础梁模拟方法研究[J].海洋工程,2013,31(4):74-78.(MENG Qingfei,HUANG Weiping.Simulation of SCR and seabed with elastic foundation beam model [J].The Ocean Engineering,2013,31(4):74-78.(in Chinese ))
[10] 李传凯.钢悬链线立管静力及波激疲劳分析[D].大连:大连理工大学,2008.(LI Chuankai.Static and wave induced fatigue analysis of steel catenary riser[D].Dalian:Dalian University of Technology,2008.(in Chinese))
[11] AUBENY C,SHI H.Interpretation of impact penetration measurements in soft clays[J].Journal of Geotechnical and Geoenvironmental Engineering,2006,132(6):770-777.
Study on method of interaction between steel catenary riser and nonlinear seabed
LIANG Ning,HUANG Weiping,YANG Chaofan
(Shandong Key Laboratory of Ocean Engineering,Ocean University of China,Qingdao 266100,China)
P751
A
10.16483/j.issn.1005-9865.2016.01.006
1005-9865(2016)01-0040-10
2015-01-07
国家自然科学基金(51179179,51239008)
梁 宁(1990-),男,山东淄博人,硕士生,主要从事海洋工程结构设计分析研究。E-mail:liangningouc@163.com
