浅水中浮体在波浪作用下运动的三维时域计算模型
2016-10-12张俊生丛培文
张俊生,滕 斌,丛培文
(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
浅水中浮体在波浪作用下运动的三维时域计算模型
张俊生,滕 斌,丛培文
(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
港口中系泊船在波浪作用下运动问题的本质是浅水波浪与浮体的相互作用。与深水情况不同,浅水问题应当考虑水底、水域边界的影响及浅水波浪自身的特性,单一模型很难实现该模拟过程。为此,建立了Boussinesq方程计算入射波和Laplace方程计算散射波的全时域组合计算模型。有限元法求解的Boussinesq方程能使入射波充分考虑到水底、水域边界的影响和浅水波浪的特性;散射波被线性化,采用边界元法求解,并以浮体运动时的物面条件为入射波和散射波求解的匹配条件。该方法为完全的时域方法,计算网格不随时间变动,计算过程较为方便。通过与实验及其他数值方法的结果进行比较,验证了本模型对非线性波面、浮体的运动都有比较理想的计算结果,显示了本模型对非线性问题具有较好的计算能力。
浅水中浮体运动;非线性波浪作用;Boussinesq方程;Laplace方程;三维时域数值模型
Abstract:The calculation of the wave-induced motion of a moored ship in a harbor is essentially a problem of calculating the wave-induced motion of a floating body in shallow water.In this case,the influence of the sea bed and boundaries as well as waves must be considered,as it is different from the problem in deep water.It is difficult to solve the problem by using a single model.Therefore,a combination of an improved Boussinesq equation,to calculate incident waves,and the Laplace equation,to calculate scattered waves,is used to establish a numerical model.The Boussinesq equation solved by the finite element method can embody the characteristics in shallow water while simulating incident waves,and scattered waves are solved by the boundary element method under the linear approximation.The two parts are matched through the boundary condition on the surface of the floating body.The present model is a full time-domain one,but computational grids do not change with the time,which makes the calculation convenient.While calculating nonlinear wave elevations and the motion of the floating body induced by nonlinear waves,the comparison of present results with experimental data and results of other numerical methods shows a good agreement and proves the combined model feasible to deal with nonlinear problems.The model is worthy of being applied to calculate the motion of the moored ship in engineering.
Keywords:motion of the floating body in shallow water; action of nonlinear waves; Boussinesq equation; Laplace equation; 3D time-domain numerical model
计算港口内系泊船在波浪作用下的运动是一个传统而远未解决的问题。准确计算需要考虑多方面问题:波浪的非线性、港口边界和地形、浮体的运动响应、系泊系统等,整个计算是一个复杂的耦合系统。其中,核心问题就是浅水中波浪作用下浮体运动响应的计算。最早比较完整地给出该问题计算的是Sawaragi & Kubo[1]。其计算是一种频域解析的方法,整个计算域被分为外域、船体与港池边界间的内域、船底下方与水底间计算域等三个部分,各部分之间通过速度势和压力连续相匹配,进行求解。计算只能假定水底为平地,港池也只能为规则的矩形,而计算条件完全采用线性假设。Weiler等[2]提出了一个计算岸壁前驻波对船体作用的频域计算方法,计算中,驻波被分离为两个反向的行进波进行考虑。鉴于频域方法对入射波特性、计算域形状等的限制,为使求解更能适用于真实、复杂的近岸港口水域,于是,一些非线性时域数值方法被不断地提出。
最有代表性的是Bingham[3]提出的一种组合型的计算方法,其通过差分法求解Boussinesq方程(以下简称“B方程”)计算入射波,通过源汇法在频域内求解线性的散射波激振力、附加质量和辐射阻尼,再通过傅里叶变换转化为时域的散射波作用力、附加质量和迟滞函数,最后把入射波和散射波的激振力相加,进而求解含有卷积积分的时域运动方程。B方程的特点是可以将三维问题简化为二维计算,使计算量大为减少,从而能够在大面积水底地形变化的浅水水域中模拟非线性波浪。因此,在系泊船运动的计算模型中应用B方程在此后的研究中被不断地采用,以使计算模型能在一定程度上考虑水域地形、边界的影响和波浪的非线性。Van Der Molen[4]也提出了类似的计算模型,但散射势的求解采用了卷积积分求解时域线性解的方法。不过,归根到底,该方法还是一种利用脉冲响应函数的算法,不是完全意义上的时域方法。王大国等[5]、Wang等[6]及王海龙等[7]给出了几个耦合时域模型,尽管形式不同,但本质上皆是内外域耦合计算的方法,外域采用B方程求解,内域采用Euler方程或Laplace方程(以下简称“L方程”)计算。该计算思路虽是非线性耦合,也是完全时域的,但最大的不足是这些模型只能适用于物体不动的情况,即模型不能考虑物体的运动,只能计算波面。故在其进行的实验中,浮体也固定不动,从而仅验证了波面计算的准确性,但该模型无法满足实际工程的需求。
这里也采用“组合”计算的方法,以B方程模拟入射波浪,以L方程计算散射波,通过运动浮体的物面条件连接两部分的计算并求解运动方程。与Bingham[3]和Van Der Molen[4]的模型相比,在浮体运动响应和散射波的计算上,采用沿时间步递进求解的方法,从而构建一个严格意义上的完全时域计算模型。在数值方法上,则采用有限元法求解B方程,以满足曲边界的计算,避免差分法处理边界不灵活的弊端;采用边界元法计算浮体的运动响应和散射波,从而既能满足浮体形状多样性的需求,又能简化三维计算。本文对散射波也做线性化处理。正如Van Der Molen[4]指出的:入射波非线性的影响是重要的,但船在港口内受波浪作用的运动幅度比较小,辐射波和绕射波比入射波小很多,因此采用线性方法计算波浪对船体的作用是有效的。也正因此,计算散射波时,地形的影响可以忽略,视水底为平地。
通过与Wang等[6]实验结果的对比,验证了本模型对非线性波面的计算能力;通过与Bai等[8]的浮体运动时域计算模型的线性波作用结果和Teng等[9]的二阶Stokes波作用下浮体运动频域计算模型的结果相比,验证了本模型的组合计算方法和衔接条件的正确性,考察了本模型对非线性波浪作用下的浮体运动的计算能力。
1 模型的建立
1.1入射波的计算
入射波浪的计算无需考虑浮体的存在。鉴于等参单元有限元法无法计算四阶及其以上导数,故采用Beji等[10]的改进型B方程计算入射波浪,方程形式为:

空间离散可以采用四边形或三角形单元;入射边界条件则为Fenton[12]的高精度非线性波解析解;固边壁上的边界条件按照Engelman等[13]方法处理,可对曲边界准确求解;根据计算的具体情况和需要,阻尼层和松弛层可分别布置在计算域出口和入射边界前,以吸收计算域内传出的波浪。时间积分方面,前四步,采用Runge-Kutta法求解,此后,采用四阶Adams-Bashforth-Moulton预报-校正方法进行计算。
1.2散射波的计算
采用L方程求解散射波,其形式为
其中,ηs为散射波波高。物面取浮体平均湿表面,物面条件为
式中:U为浮体上某一点运动速度矢量,n=(n1,n2,n3)为该点处指向物体内的物面单位法向向量,φI为入射势。浮体被看作刚体,其位移和转角矢量分别为ξ=(ξ1,ξ2,ξ3)、χ=(χ1,χ2,χ3),在小转角假定下有
其中,x(x,y,z)为所求点坐标,xr(xr,yr,zr)为转动中心坐标。将式(7)代入式(6),并进一步转化,可得
令(ξ4,ξ5,ξ6)=χ,(n4,n5,n6)=(x-xr)n,式(8)可简写为
其中,N=(n1,n2,n3,n4,n5,n6)为指向物体内的广义物面单位法向向量,ξ也扩为6维向量(ξ1,ξ2,ξ3,ξ4,ξ5,ξ6)。φI/n=φIn=uIn是散射波和入射波相衔接的条件。uI为入射波的质点速度,可由求得,其水平分量uI、vI近似到二阶的沿水深分布表达式为
对应的垂向分量wI的表达式为
wI=-
以边界元法求解散射波时,水底被看作不透水的平地。采用Rankine源及其关于海底的像作为格林函数
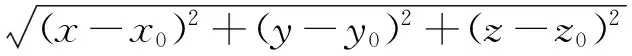
计算中,网格固定不变。通过式(4)、(5)可求得每一时间步自由水面上的ηs、φs;通过式(9),可求得物面上的φs/n。通过这些边界条件,利用边界元法,可求得自由水面上的φs/n(线性情况下,为z=0面上的φs/z)和物面上的φs,前者结合ηs通过式(4)、(5)可进一步求得下一时间步自由水面上的ηs、φs,后者可用于计算浮体受力,利用运动方程求得下一时间步的浮体运动位移,再通过式(9)计算物面上的φs/n,以此往复,在时间域上持续求解。对于计算散射波时的时间积分,这里采用四阶Runge-Kutta法。
1.3浮体运动的计算
对于波浪与浮体作用的问题,浮体运动以及其产生的辐射波必须予以考虑。不同于Bingham和Van Der Molen在计算中使用含有迟滞函数和附加质量的运动方程,本模型在时域内直接计算辐射波及其作用力,浮体的运动方程采用下式求解:

其中,M、B、C分别为浮体质量阵、黏性阻尼系数阵、恢复力矩阵,均为66的方阵,M和C需要根据物体质心和质量分布计算得出,具体求解过程参见李玉成和滕斌[14]给出的方法;F(t)为六个分量的广义波浪激振力,包括入射波和散射波的共同作用;G(t)为系泊系统等其它外部作用力和力矩。该方程包含了6个广义方向的运动:纵荡(ξ1沿x轴)、横荡(ξ2沿y轴)、垂荡(ξ3沿z轴)、横摇(ξ4绕x轴)、纵摇(ξ5绕y轴)、回转(ξ6绕z轴)。系泊系统等外部作用力G(t),如缆绳、护舷等,在具体工程估算中,可以由计算中求出的缆绳、护舷变形结合产品力学性能曲线获得;理论计算中,可由缆绳、护舷理论模型求得。本文不对G(t)进行具体分析求解,只集中考虑波浪激振力F(t)对浮体的作用,计算后文算例时,仅在式(13)中加入刚度阵K(式左侧加入Kξ(t)项),代替系泊系统,以保证浮体能围绕某一平衡位置运动。
通过流体动压强p在物面的平均湿表面Ωb上积分求解波浪激振力:
同样,p可分为入射波和散射波产生的动压强pI、ps。根据B方程理论,pI沿水深分布的二阶表达式为
ps的线性结果为
运动方程的时间积分也采用Runge-Kutta法,与散射波时间积分同步求解。如果把式(13)抽象表述为
则浮体运动位移和速度的时间积分表达式为



2 模型验证
2.1波面计算的验证
Wang等[6]开展了一个波浪对箱型船绕射的实验,实验中箱型船被固定住,并通过浪高仪测定了一些位置的波高。现利用该实验结果检验本模型对非线性问题的处理能力。
实验水池长31 m、宽14 m,实验水深为0.3 m,实验所用箱型船长l=2.0 m、宽B=0.6 m、高h=0.45 m、吃水dr=0.24 m。具体船与浪高仪的布置如图1所示。在静水面上,以箱形船的几何中心为原点,建立方向如图1所示的坐标系,表1给出了24个测点的坐标。实验中,入射波浪周期为T=3.0 s,波高为H0=0.03 m。
由实验布置可以看出,水池的上下两个边壁与船模型的距离并不远,对散射波浪场亦会产生影响,故计算散射波时需要对两侧边壁作些处理。如1.2节所述,在格林函数中,加入源点关于一侧边壁的像,从而去掉该侧边壁的面积积分,简化计算。另一侧边壁,则需进行网格划分,参与计算,其上的边界条件为φs/n=0。计算中为保证船不动,需取K足够大,文中取其对角线元素为1020。

图1 Wang等实验布置图 Fig.1 Layout of Wang et al.’s experiment

表1 测点位置Tab.1 Positions of the test points
Wang等给出了波浪场稳定后,两个周期内各测点上波高变化曲线。图2展示了本文模型计算结果与实验结果的对比。尽管本模型对散射波做了线性化处理,致使在某些测点上存在次波峰的差异,但从波高变化曲线的整体上观察,本计算与实验结果相当一致。可见,在散射波线性化处理的情况下,本模型对波浪非线性还是有较强的模拟能力,这从一方面体现了本模型的有效性,也证明了Van Der Molen的说法:散射波相比于入射波很小,可线性化处理。
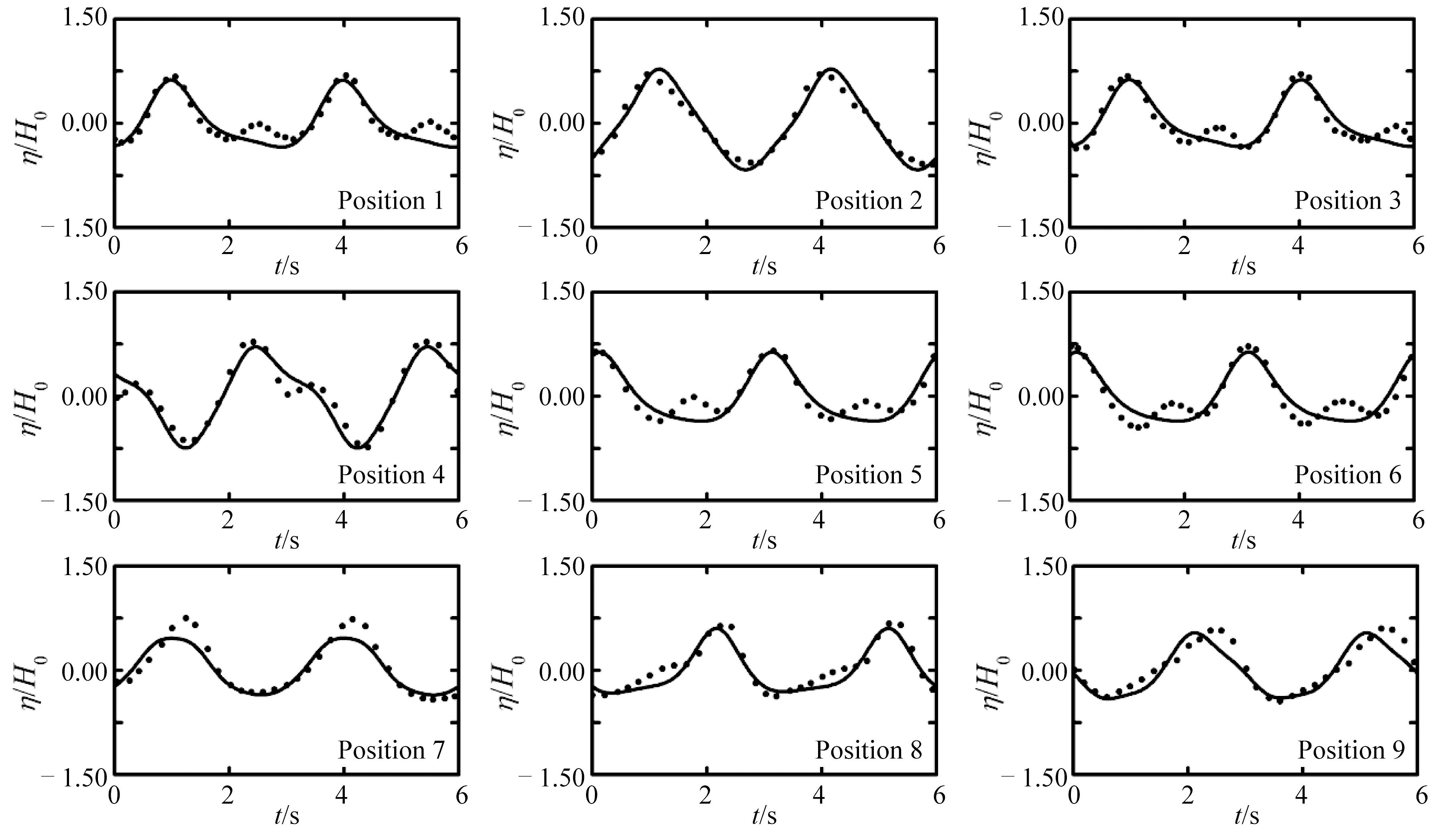

图2 各测点上计算波高与实验结果比较Fig.2 Comparison of wave elevations at the test points
2.2浮体运动计算的验证
Bai等[8]和Teng等[9]分别给出了开敞水域中浮体在二阶Stokes波作用下运动的时域和频域计算模型,并对模型的有效性进行了充分验证。本文计算浮体运动的结果将分别与该两种模型的结果进行比较,以验证本文对浮体运动计算的能力。

图3 被测试浮体的示意Fig.3 Sizes of the floating body tested
如图3所示,取开敞的计算水域水深为d=0.5 m,漂浮于水面上的箱形船长l=4.2 m、宽B=0.6 m、高h=0.5 m、吃水dr=0.3 m,计算中取箱形船为均质,质心oc为其形心。以质心垂直投影到静水面所得之点为原点o,建立坐标系,x轴沿船长方向,y轴沿船宽方向,z轴沿垂直方向。计算时,取原点o为转动中心。
测试波浪为4组,周期皆为T=1.8 s,波高由低到高分别取H0=0.012 m、0.036 m、0.072 m和0.108 m,相应的波陡分别为H0/L=0.34%、1%、2%、3%,均沿y方向入射。根据《The Shore Protection Manual (1984)》,可以大体判断出四组波浪的非线性和适用理论,如图4所示。很明显,Case 1(H0=0.012 m)可以被看作线性波,适用于线性理论求解;Case 2(H0=0.036 m)、Case 3(H0=0.072 m)、Case 4(H0=0.108 m)则皆适用于二阶Stokes波理论求解。
为便于计算结果的比较,需要保证浮体在波浪激振力作用下于某一平衡位置做简谐振动,故在计算中需要给出刚度阵K和黏性阻尼系数阵B。刚度阵中,取k22=450,k44=24,其余元素取0;黏性阻尼系数阵中,取b22=470,b44=25,其余元素取0。

图4 测试波浪的适用理论Fig.4 Appropriate theories for the tested waves
图5给出了本模型和Bai等的浮体运动时域计算模型对Case 1的计算结果。纵荡ξ1、纵摇ξ5、回转ξ6始终为0,故只给出横荡ξ2、垂荡ξ3、横摇ξ4的历时曲线。可以明显地看到,除因初始状态不同而致使前面若干个周期有差异外,两者的计算结果在浮体运动稳定之后完全一致。这证明了本模型作为一种组合模型,计算入射波的B方程和计算散射波的L方程相互间的衔接条件是合理的,匹配过程是准确的。图6给出了本模型和Teng等的二阶Stokes波作用下浮体运动频域计算模型对Case 2、3、4的计算结果,这里只计算浮体的周期运动,未考虑浮体因平均漂移力而产生的定常位移。同样只给出ξ2、ξ3、ξ4的历时曲线,其余方向的运动始终为0。可以直观地看到,整体上,本模型与二阶Stokes理论的频域计算结果吻合较好,显示出:尽管对散射波做了线性化处理,但本模型仍能在一定程度上对浮体在非线性波浪作用下的运动进行模拟和计算。进一步观察可以发现,在波陡从1%增加到3%的过程中,文中计算的运动幅值会逐渐小于二阶Stokes理论的频域结果。波浪非线性越强,偏小的程度就越略大一些,这是散射波线性化的必然结果。由图4可知,Case 4的波浪非线性已经比较可观,但这里计算结果与二阶Stokes理论结果仍比较接近;而另一方面,一般认为在港池中波浪的非线性不会太强,所以,本模型就系泊船的运动而言,对非线性波浪的计算能力是可以接受的。
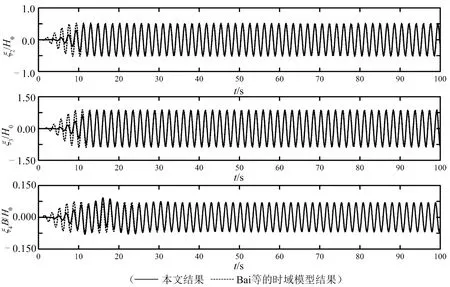
图5 线性波作用下浮体运动的计算结果比较(T=1.8 s,H0=0.012 m)Fig.5 Comparison of calculated results for the motion of the floating body induced by a linear wave (T=1.8 s,H0=0.012 m)


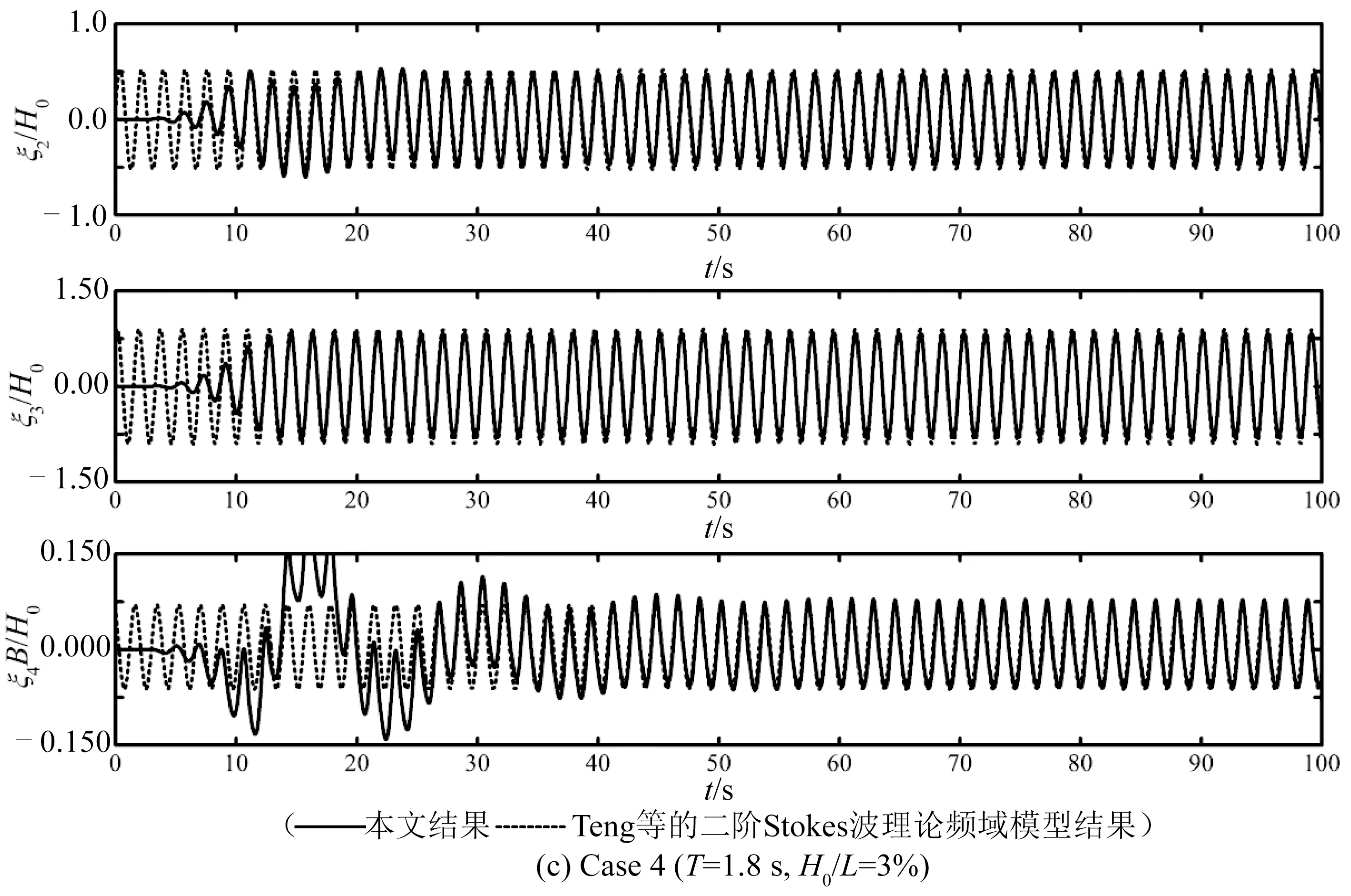
图6 二阶Stokes波作用下浮体运动的计算结果比较Fig.6 Comparison of calculated results for the motion of the floating body induced by 2nd order Stokes waves
3 结 语
港口中波浪作用下系泊船运动问题的核心是计算浅水中浮体在波浪作用下的运动。而相比于深水问题,海底地形、水域边界的影响和浅水波浪特性成为应该考虑的必要因素,因此,建立含有B方程的组合模型成为一种有效的方法。相比于已有的模型,文中建立的B方程和L方程的组合模型是一个能有效计算浮体运动的完全时域模型。采用有限元法求解B方程模拟入射波,在体现浅水波浪特性和水底影响之外,与差分法相比又能较好地处理曲边界的影响。散射波的线性化使计算得到简化,浮体的物面积分也只需在平均湿表面上进行,在时域求解过程中网格也始终保持不变,从而使整个求解过程相对简单、方便。
通过与Wang等实验结果的对比,体现了本模型对非线性波浪的计算能力;在计算线性波作用下浮体的运动时,本文结果与Bai等的时域模型结果完全一致,说明了本模型作为组合模型,各计算部分的匹配和计算过程是准确的。在计算二阶Stokes波作用下浮体的运动时,本文结果与Teng等的二阶Stokes理论频域模型的结果也基本一致,表现出本模型对非线性问题有较理想的计算能力。
综上可见,本模型是一个计算过程较简单、能在较大程度上计算出浅水中浮体在非线性波浪作用下运动响应的组合模型。可以预期,该模型在不断完善之后,能够成为工程中估算系泊船运动的有效工具。
[1] SAWARAGI T,KUBO M.The motion of a ship in a harbor basin[C]//Proc.18th ICCE.1982,3:2743-2762.
[2] WEILER O M,DEKKER J.Mooring container ships exposed to long waves[C]//Proc.13th Int.Harbor Congress.2003.
[3] BINGHAM H B.A hybrid Boussinesq-panel method for predicting the motion of a moored ship[J].Coastal Engineering,2000,40:21-38.
[4] VAN DER MOLEN W.Behavior of moored ships in harbors[D].Delft:The Water Research Center of The Delft University of Technology,2006:55-68.
[5] 王大国,邹志利,唐春安.波浪对箱形船作用的三维耦合计算模型[J].船舶力学,2007,11(4):533-544.(WANG Daguo,ZOU Zhili,TANG Chunan.Time stepping solutions of nonlinear wave forces on a three-dimensional box-shaped ship in a harbor[J].Journal of Ship Mechanics,2007,11(4):533-544.(in Chinese))
[6] WANG D G,ZOU Z L,TANG C A.A three-dimensional coupled numerical model of nonlinear waves in a harbor[J].Science in China Series E,Technological Sciences,2008,51(12):2195-2206.
[7] 王海龙,邹志利,周亚龙,等.波浪对圆柱作用的三维耦合计算模型[J].中国海洋平台,2010,25(5):38-48.(WANG Hailong,ZOU Zhili,ZHOU Yalong,et al.The three-dimensional coupled numerical model of non-linear wave acting on a circular cylinder[J].China Offshore Platform,2010,25(5):38-48.(in Chinese))
[8] BAI W,TENG B.Second-order wave diffraction around 3-D bodies by a time-domain method[J].China Ocean Engineering,2001,15(1):73-85.
[9] TENG B,EATOCK R.A BEM method for the second-order wave action on a floating body in monochromatic waves[C]//Proc.1st Int.Conf.on Hydrodynamics.1994:274-281.
[10] BEJI S,NADAOKA K.A formal derivation and numerical modeling of the improved Boussinesq equations for varying depth[J].Ocean Engineering,1996,23(8):691-704.
[11] LI Y S,LIU S X,YU Y X,et al.Numerical modeling of Boussinesq equations by finite element method[J].Coastal Engineering,1999,37:97-122.
[12] FENTON J D.The numerical solution of steady water wave problems[J].Computers & Geosciences,1988,14:357-368.
[13] ENGELMAN M S,SANI R L.The implementation of normal and/or tangential boundary conditions in finite element codes for incompressible fluid flow[J].International Journal for Numerical Methods in Fluids,1982,2:225-238.
[14] 李玉成,滕斌.波浪对海上建筑物的作用(第二版)[M].北京:海洋出版社,2002:70-73.(LI Y C,TENG B.Wave action on maritime structures (2nd edition)[M].Beijing:China Ocean Press,2002:70-73.(in Chinese))
A 3D time-domain numerical model for floating body motion
induced by shallow water waves
ZHANG Junsheng,TENG Bin,CONG Peiwen
(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)
TV139.2
A
10.16483/j.issn.1005-9865.2016.01.001
1005-9865(2016)01-0001-09
2014-11-23
国家自然科学基金面上项目(51379032);国家自然科学基金重大项目(51490672)
张俊生(1980-),男,辽宁大连人,助理研究员,博士生,从事波浪对海上结构物作用的研究。E-mail:yzjz009@126.com
滕 斌。E-mail:bteng@dlut.edu.cn
