一种改进的辅助函数法及其对近似长水波方程的求解

邱　春

(四川建筑职业技术学院土木工程系，四川德阳618000)



一种改进的辅助函数法及其对近似长水波方程的求解

邱春

(四川建筑职业技术学院土木工程系，四川德阳618000)

提出一种求解非线性演化方程的改进的辅助函数法，根据不同的参数可给出不同形式的精确解，从而有助于探索非线性方程的新解.用此方法求解了近似长水波方程，得到了其多组精确解.

改进的辅助函数法；辅助方程；近似长水波方程

非线性演化方程在物理学等领域有着重要的作用，而这些方程的准确求解可以帮助我们更好的理解其动力学特征，因而寻找非线性演化方程的精确解尤为重要，近年来涌现出一系列求解方法，如：齐次平衡法，[1]Jacobi椭圆函数展开法,[2]sine-cose方法,[3]双曲函数展开法,[4]辅助方程法,[5]使用这些方法，人们获得了非线性演化方程大量精确解.本文提出了一种改进的辅助方程法，并用之求解了近似长水波方程，结果表明该方法是方便是有效的.

1　方法介绍

设非线性演化方程一般形式为

(1)

式中f是其参数的多项式函数，引入行波变换

(2)

c为待定波常数

将(2)式代入(1)式得到关于U,U',U''...的常微分方程

(3)

式中“U'”表示导数dU/dξ.

设方程 (3) 的解为如下形式

(4)

其中ai，bi为待定常数，n由(3)中U的最高阶导数项与非线性项平衡来确定, F(ξ) 及G(ξ)为辅助函数，且满足如下微分方程组

(5)

且满足

(6)

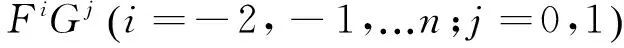
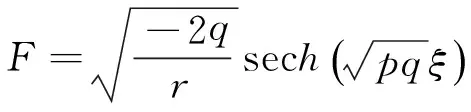
(7)

2　近似长水波方程的求解

考虑如下形式的长水波方程[7]

(8)

引入行波变换

(9)

式中c待定波速常数，将(9)式代入(8)式，经过简单变形有

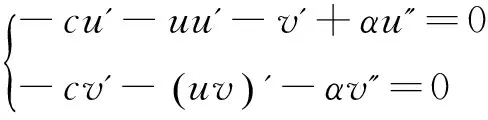
(10)

将(10)式中两方程关于ξ积分一次得到下式

(11)

式中C1，C2为积分常数

平衡方程(11)第一式中u'和v， 第二式中v'和uv可知m=1，n=2, 于是方程(11)有如下形式的解.

(12A)

(12B)

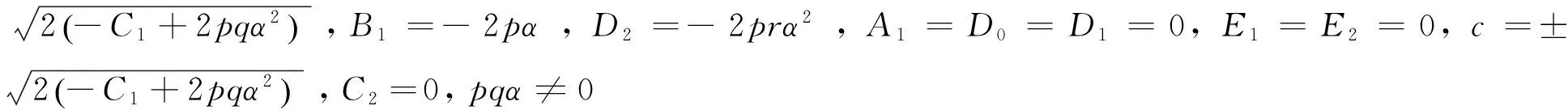
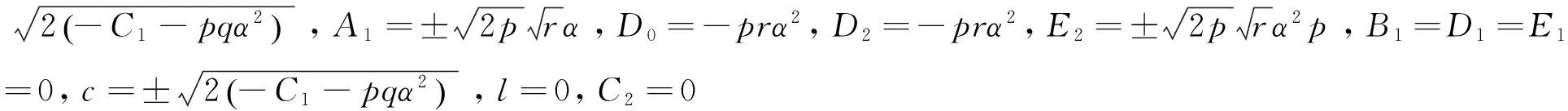
将以上4组解的系数代入式(12A)及(12B)，并结合F和G表达式可得出近似长水波方程(8)式对应的精确解

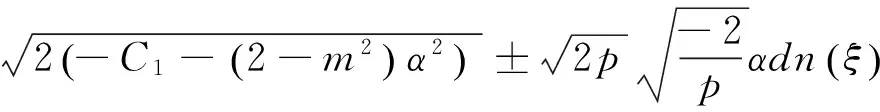
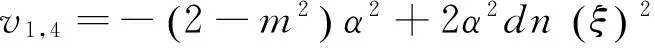
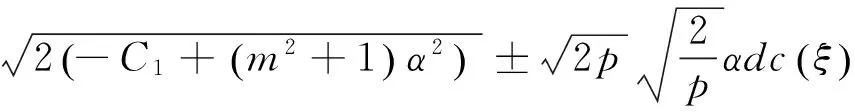
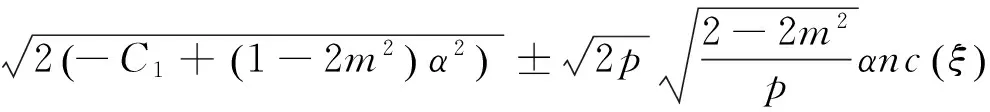
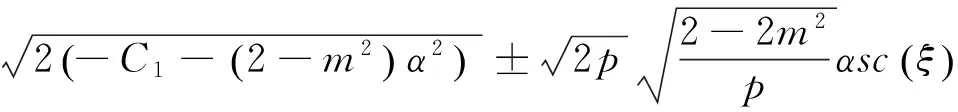
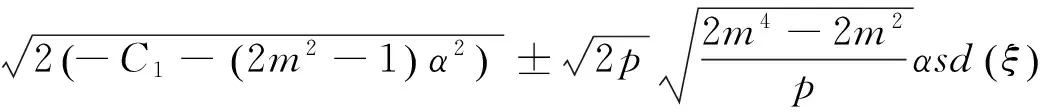
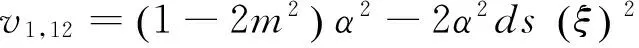
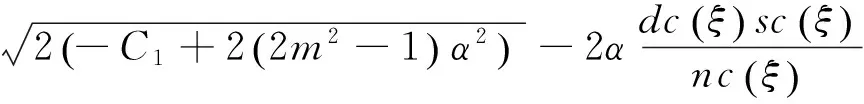
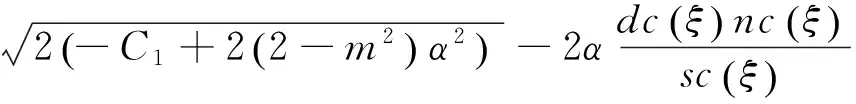
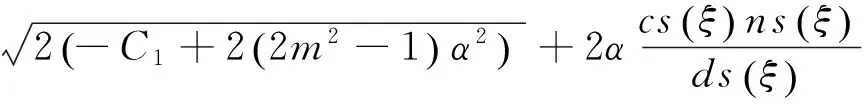
说明：

1)以上各种情况下的解必须满足对应的系数约束条件

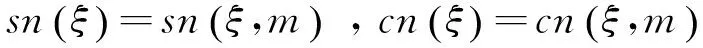
3　结论

本文采用一种改进的辅助微分方程法求解了近似长水波方程，得到其多组精确行波解，包含部分新解，这些解有助于我们更好的理解波的传播机理，因而有着重要的应用价值；此方法简单易行，具有一定的普遍性，也可用于探索其它非线性方程的新解.

[1] Fan E G, Zhang H Q.NewexactsolutionstoasystemofcoupledKdvequations[J]. Phys Lett A, 1998(5):389-392.

[2] Liu S K, Fu Z T, Liu S D, Zhang Q et al.Jacobiellipticfunctionexpansionmethodandperiodicwavesolutionsofnonlinearwaveequations[J]. Phys Lett A,2001(1):69-74.

[3] Yan C T.Asimpletransformationfornonlinearwaves[J]. Phys Lett A, 1996(1):77-84.

[4] Fan E G.Extendtanh-functionmethodanditsapplicationstononlinearequations[J].Phys Lett A, 2000(4-5):212-218.

[5] Fan E G.Anewalgebraicmethodforfindingthelinesolitonsolutionsanddoublyperiodicwavesolutiontoatwo-dimensionalperturbedKdvequation[J]. Chaos Solitons Fractals, 2003(3):567-574.

[6]刘式适，刘式达. 物理学中的非线性方程[M]. 北京：北京大学出版社, 2001:47-56.

[责任编辑范藻]

An Improved Auxiliary Function Method and Its Applications for the Approximate Long Water Wave Equations

QIU Chun

( Civil Engineering School of Sichuan College of Architecture Technology, Deyang Sichuan 618000, China)

In this paper, we present a new improved auxiliary method and use it to investigate the approximate long water wave equations; as a result, more explicit solutions according to some parameters are obtained, some of which are new.

improved auxiliary function method; auxiliary equation; the approximate long water wave equations

2016-04-15

德阳市重点科学技术研究项目(2014ZZ095-3)

邱春(1976—)，男，江苏徐州人.工程师，博士，主要从事工程水力学及非线性方程研究.

O175

A

1674-5248(2016)05-0013-04