关于斜坡信号的傅里叶变换探讨——从一则悖论谈起

王益艳，伍世云

(四川文理学院智能制造学院，四川达州635000)



关于斜坡信号的傅里叶变换探讨
——从一则悖论谈起

王益艳，伍世云

(四川文理学院智能制造学院，四川达州635000)

斜坡信号作为一种特殊的奇异信号，由于不满足绝对可积的条件，在计算傅里叶变换时如果采用传统方法往往会遇到困难.若采用傅里叶变换时域卷积定理，将导致一个悖论产生.从该悖论入手，对斜坡信号傅里叶变换的求解方法进行了探讨，给出了三种新的计算方法，最后分析了悖论引起的原因.

斜坡信号；傅里叶变换；悖论；广义函数

0　引 言

傅里叶变换是一种非常重要的时频信号分析工具，已被广泛应用于电力工程、通信和控制等领域.[1]对周期信号进行时频分析时，需要利用其傅里叶级数展开，而求解傅里叶级数，必须满足“狄利克雷”条件.[2]而对非周期信号而言，其傅里叶变换公式可表示为：[3]

(1)

其中，f(t)为时域连续信号，F(jω)为其对应的傅里叶变换.

一般来说，只要所给信号的上述积分收敛，其傅里叶变换就有意义.即要求满足如下绝对可积的条件：[3]

(2)

其中，M为常量.但式(2)只是傅里叶变换存在的充分条件，并不是必要条件.某些常用信号(如周期信号、阶跃信号、符号函数等)并不满足式(2)绝对可积的条件，但可以借助广义函数(如冲激函数)的概念，[4]求解它们对应的傅里叶变换.

斜坡信号t·ε(t)作为一种特殊的奇异信号，显然也不满足绝对可积的条件.虽然可从现有的《信号与系统》教科书后面附录“常见信号傅里叶变换表”中查到其傅里叶变换为：[5,6]

(3)

但王道宪等人对该结论提出了质疑.[7]由于

(4)

f1(t)*f2(t)⟺F1(jω)·F2(jω)

(5)

可以得出：

(6)

显然，式(3)和式(6)结果不相等(实部和虚部分别对应不相等).根据信号傅里叶变换结果的唯一性，同一信号不可能产生两种截然不同的频谱？于是产生了悖论.

1　斜坡信号傅里叶变换方法探讨

王道宪等人对上述矛盾结果进行了探讨，指出产生悖论的原因在于傅里叶变换本身所存在的不足：[7]只给出了傅里叶变换存在的充分条件，没指出其所应满足的必要条件.其实不然，为了作比较，本文先给出三种新的计算斜坡信号傅里叶变换的方法.同样，也是利用傅里叶变换的性质.

(7)

而根据普通函数与冲击偶函数乘积的定义：[8]

f(t)·δ′(t)=f(0)·δ′(t)-f′(0)·δ(t)

(8)

令f(t)=t，式(8)容易推出t·δ′(t)=-δ(t)，进行变量代换得ω·δ′(ω)=-δ(ω).因此式(7)可变为：

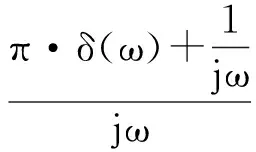
(9)

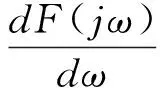
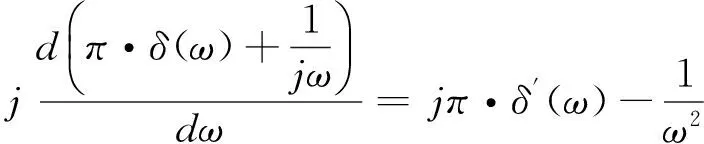
(10)

(11)

式(11)的化简利用了以下冲激函数卷积的两条性质：[9]

f(t)*δ(t)=f(t)，f(t)*δ′(t)=f′(t)

(12)

由上述分析可知，式(9)、(10)和(11)对斜坡信号计算傅里叶变换得到的结果相等，且与教材中附录表给出的结论一致(见式(3))，唯独与式(6)结果矛盾.观察式(6)、(9)、(10)和(11)中间运算步骤就会发现：在计算过程中都利用了冲激函数δ(t)或冲激偶函数δ′(t)的乘积、微分或卷积运算.而冲激函数或冲激偶函数都属于广义函数，它不符合普通函数的定义，并且冲激函数具有自身一些独有的性质.下面通过广义函数的性质分析上述矛盾结果产生的原因.

2　广义函数的定义及上述悖论的根源

广义函数g(t)的定义为：[10]

(13)

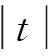
按广义函数理论，冲激函数δ(t)可定义为：

(14)

其中，φ(t)在冲激时刻t=0处连续.上式表明，广义函数δ(t)具有筛选性质，即可从φ(t)中筛选出φ(0)的值.

冲激函数可以求导，求积分，也可以与普通函数进行乘积或卷积，冲激函数之间也可以进行卷积.[9-10]比如：

冲激函数δ(t)的一阶导数δ′(t)可定义为：

(15)

δ(t)的积分为：

(16)

其中，ε(t)为阶跃函数.

冲激函数δ(t)与普通函数f(t)的乘积：

f(t)·δ(t)=f(0)·δ(t)

(17)

冲激函数δ(t)与普通函数f(t)的卷积：

f(t)*δ(t)=f(t)

(18)

冲激函数δ(t)与冲激函数δ(t)的卷积：

δ(t)*δ(t)=δ(t)

(19)

但是，由于广义函数自身之间不能进行乘法运算，[11]因此δ(t)·δ(t)没有定义.[12]在上一节中，分别采用时域微分、频域微分、频域卷积定理等三种不同方法，在求解斜坡信号傅里叶变换过程中，式(9)、(10)和(11)分别利用的是冲激函数与普通函数的乘积、冲激函数的微分、冲激函数与冲激函数的卷积等性质.而采用时域卷积定理方法计算斜坡信号的傅里叶变换，式(6)中出现了δ2(ω)，即两个冲激函数直接相乘，它没有定义，所以该结果不正确.因此，对斜坡信号，不能采用时域卷积定理求其傅里叶变换.

3　结论

斜坡信号作为一种特殊的奇异信号，它既不是能量信号，也不是功率信号.在计算其傅里叶频谱时，由于不满足绝对可积的条件，如果采用传统方法往往会遇到困难.通过引入广义函数(如冲激函数δ(t))，再借助卷积积分和傅里叶变换的性质，可使问题简单化.本文从一个悖论结果出发，对斜坡信号的傅里叶变换方法进行了简要探讨，给出了三种新的计算方法，最后指出了悖论产生的原因，有利于人们加深对广义函数的理解.

[1] Vretblad A.FourierAnalysisandItsApplications[M]. Berlin：Spring-Verlag, 2003: 23-26.

[2] B.P. 拉兹. 线性系统与信号[M].刘树棠，王微洁，译.西安: 西安交通大学出版社, 2006: 473-474.

[3] 金波, 张正炳. 信号与系统分析[M]. 北京: 高等教育出版社, 2011: 315-316.

[4] Philips L, Parr M, Riskin E A.Signals,Systems,andTransforms[J].International Journal of Gynecology & Obstetrics,2009(S2):S416.

[5] 郑君里, 应启珩, 杨为理. 信号与系统:上[M]. 北京: 高等教育出版社, 2011: 404-405.

[6] 王宝祥. 信号与系统[M]. 北京: 电子工业出版社, 2010: 305-306.

[7] 王道宪, 段晓辉, 杨光临.关于信号傅里叶变换存在条件问题的探讨[J]. 电子与信息学报, 2013(11)：2790-2793.

[8] 刘泉, 江雪梅. 信号与系统[M]. 北京: 高等教育出版社, 2006: 22-23.

[9] 郭银景. 信号与系统[M]. 北京: 机械工业出版社, 2009：41-42.

[10]陈生潭, 郭宝龙, 李学武,等. 信号与系统[M]. 西安: 西安电子科技大学出版社, 2008：18-19.

[11]L.施瓦兹. 广义函数论[M]. 姚家燕,译.北京: 高等教育出版社, 2010：83-84.

[12]吴大正. 信号与线性系统分析[M]. 北京: 高等教育出版社, 2008：18-19.

[责任编辑范藻]

The Paradox in Fourier Transform of Ramp Signal

WANG Yiyan,WU Shiyun

(Intelligent Manufacturing School of Sichuan University of Arts and Sciences, Dazhou Sichuan 635000, China)

The ramp signal, as a special singular signal, calculating its Fourier transform by the traditional methods has encountered a difficult problem, because the condition of absolutely integrable is not satisfied, while calculating by Fourier transform time domain convolution theorem, a paradox will be resulted. In this paper, the method for solving the Fourier transform of ramp signal is discussed from the start of the paradox, then three new calculation methods are presented, and finally the reason of the paradox caused is analyzed.

ramp signal; Fourier transform; paradox; generalized function

2016-03-07

四川文理学院教改重点项目(2013JZ12)；四川文理学院教改一般项目(2013JY32)

王益艳(1982—)，男，湖北咸宁人.讲师，硕士，主要从事信号与图像处理研究.

TP391

A

1674-5248(2016)05-0036-03