前提嵌套程序和基数约束程序的简洁性研究*,†
2016-10-09张燕
张燕
中山大学逻辑与认知研究所
zhang85@mail2.sysu.edu.cn
沈榆平
中山大学逻辑与认知研究所
shyping@mail.sysu.edu.cn
赵希顺
中山大学逻辑与认知研究所
hsszxs@mail.sysu.edu.cn
前提嵌套程序和基数约束程序的简洁性研究*,†
张燕
中山大学逻辑与认知研究所
zhang85@mail2.sysu.edu.cn
沈榆平
中山大学逻辑与认知研究所
shyping@mail.sysu.edu.cn
赵希顺
中山大学逻辑与认知研究所
hsszxs@mail.sysu.edu.cn
直观地说,简洁性是指一个逻辑系统紧凑表示问题的能力。近年来关于简洁性的研究逐渐得到人们的关注。本文将讨论两类逻辑程序,即基数约束程序(Cardinality Constraint Programs,CCP)与前提嵌套程序(Nested Logic Programs,NLP)之间的简洁性。我们设计了一个从CCP到NLP多项式长度的等价翻译,这极大改进了Ferraris和Lifschitz提出的指数长度翻译方法,由此证明NLP至少与CCP一样简洁。
简洁性;回答集;基数约束程序;前提嵌套程序
1 引言
逻辑系统的简洁性指该系统紧凑表示问题的能力。简单地说,对于系统C 和C′,若C′中的每个理论都可等价翻译(不添加辅助变元)为C中的理论而不会引起该理论长度的指数增长,则称C至少与C′一样简洁(C′≾C)。最近,对基于回答集语义的逻辑程序(Answer Set Programs,ASP,[1,5,7])的简洁性研究已经引起领域内的兴趣。([8,12])ASP是处理规划、诊断、常识推理等应用的一种人工智能逻辑,它包括许多子类,如基数约束程序(Cardinality Constraint Programs,CCP,[3])、前提嵌套程序(Nested Logic Programs,NLP,[9])等。人们已经知道CCP和NLP有相同的表达能力(它们与命题逻辑等价)和推理复杂性(一致性检测为NP-完全,[3,9,12]),但它们之间的相对简洁性尚无明确结论。
本文将证明CCP≾NLP,即NLP至少与CCP一样简洁,或者说,每一个CCP程序都可以等价翻译为一个多项式长度的NLP程序。具体而言,CCP是一类含有基数约束(Cardinality Constraints,CC)的程序,即允许在文字集上表达数值约束的程序,而NLP是一类允许规则前提有命题嵌套公式的程序,此处的命题嵌套公式指由弱否定符(not)、析取符(;)和合取符(,)在文字集上形成的表达式。在2005年,Ferraris和Lifschitz([3])对CCP程序与NLP程序之间的等价翻译关系进行了深入研究,他们构造了一个从CCP程序到NLP程序的等价翻译,但该翻译一般会导致程序长度产生指数增长,因此并没有回答CCP与NLP之间的简洁性问题。
在本文中,我们通过基于布尔函数([11,14])的紧凑表示技术将上述翻译降低为多项式长度,并在此基础上证明CCP≾NLP。我们对Ferraris和Lifschitz的工作改进主要在于将基数约束拆分为计数函数、比较函数并将它们改写成多项式长度的嵌套表示,最终得到多项式长度的等价翻译。本文第二部分回顾基本知识;第三部分回顾Ferraris和Lifschitz的的构造方法;第四部分是主要证明过程,最后得到相关结论。
2 基础知识
一个字母表Σ为一个有穷原子集合。一个正文字是Σ中的一个原子(或命题变元)x。一个负文字是Σ中的一个原子x的否定not x。正文字或负文字均称为文字。按习惯,我们约定在讨论中均预设了一个字母表。
2.1基数约束程序
下面的背景来自[3,10]。一个基数约束是形如:

的表达式,其中ci(i=1,2,...,m)是文字,L,U是整数或是−∞,+∞之一。若L=−∞,则L可以省略;若U=+∞,则U可以省略。为方便,也可忽略≤号,记(1)为L{c1,...,cm}U。

一条CCP规则是形如:的表达式,其中n≥0,C、Ci(i=1,2,...,n)为基数约束。我们称C1...,Cn为该规则的前提,C为该规则的结论。若n=0,则(2)可记为C←(或C←⊤)。
一个CCP程序Π是有穷条规则(2)组成的集合。一条规则(2)的长度是指基数约束C和Ci(i=1,2,...,n)的总个数。一个CCP程序Π的长度|Π|指Π中所有规则的长度之和。
令I为原子集合,x∈Σ为一个原子,称I满足x,记为I|=x,如果x∈I。称I满足not x,如果I⊭x。我们约定I总满足⊤,且永不满足⊥。对于基数约束C,记lit(C)为C中出现的所有文字的集合。记v(C,I)为C中被I满足的文字的个数,即v(C,I)=|{c∈lit(C):I|=c}|。令C为基数约束L{c1,...,cm}U,若L≤v(C,I)≤U,则称I满足C,记为I|=C。
对规则C←C1,...,Cn,如果I满足C或I不满足前提中某个Ci(i= 1,...,n),那么称I满足此规则。如果I满足程序Π中所有规则,则称I满足Π(或I在Π下封闭),记为I|=Π。
例1考虑下面的CCP规则:
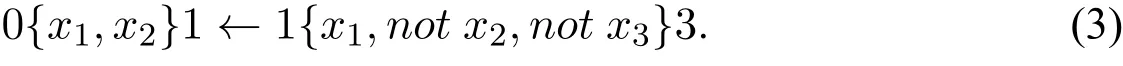
原子集{x1,x2}满足其前提,因为v(1{x1,not x2,not x3}3,{x1,x2})=|{x1,not x3}|=2,但{x1,x2}不满足其结论,因为v(0{x1,x2}1,{x1,x2})=|{x1,x2}|=2。据定义,{x1,x2}不满足规则(3)。此外,可观察到原子集{x2,x3}不满足其前提,因为v(1{x1,not x2,not x3}3,{x2,x3})=|∅|=0。据定义,{x2,x3}满足规则(3)。
对基数约束C,令atom(C)为C中出现的正文字集合,即{x∈lit(C):x∈Σ是原子}。一个形如L≤lit(C)的基数约束C相对于原子集合I的归约,记为CI,是一个基数约束L′≤atom(C),其中L′=L−|{not x∈lit(C):I|=not x}|。
例2令C为2{x1,not x2,not x3},I={x1,x2}。注意atom(C)={x1},且{x1,x2}满足C中的负文字not x3,L′=2−|{not x3}|=1,因此CI为L′≤atom(C)=1{x1}。
给定规则C←C1,...,Cn和原子集I,其中每个Ci形如Li≤lit(Ci)≤Ui,那么该规则相对于I的归约为以下规则的集合:
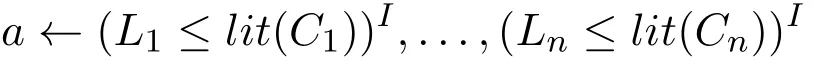
如果对每个i∈{1,...,n},I|=lit(Ci)≤Ui,其中a∈atom(C)∩I;否则,为∅。
例3规则1{x1,x2}2←1{not x2,x3}3相对于{x1,x3}的归约是
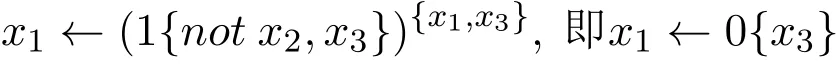
一个CCP程序Π相对于原子集I的归约ΠI是Π中所有规则相对于I的归约的并集。我们记Cn(ΠI)为满足ΠI的极小原子集。注意ΠI不含not,且Cn(ΠI)是唯一的。若I=Cn(ΠI)且I|=Π,则称I为Π的回答集。
例4令Π为程序1{x1,not x2}2←。可观察到Π有两个回答集:∅和{x1}。因∅|=Π,且Cn(Π∅)=Cn(∅)=∅;类似地,{x1}|=Π且Cn(Π{x1})= Cn({x1←})={x1}。再考虑程序{x1,x2}←,可观察到∅,{x1},{x2},{x1,x2}均为其回答集。比如,{x1,x2}|={x1,x2}←,且Cn({{x1,x2}←}{x1,x2})= Cn({x1←,x2←})={x1,x2}。
关于CCP的更多细节,可参考[3,10]。
2.2前提嵌套程序(NLP)
下面的背景来自[9]。令Σ为字母表,一个NLP公式F定义如下:
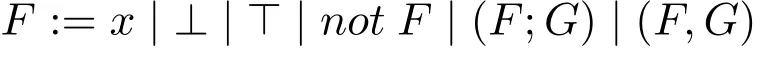
其中x∈Σ,⊥和⊤是零元连接词,弱否定符(not)是一元连接词,合取符(,)和析取符(;)是二元连接词。
一个NLP程序Π是有穷条如下形式的规则组成的集合:

其中F为原子或⊥,称为结论,G为公式,称为前提。一个NLP程序Π的长度|Π|指Π中连接词的总数。若F=⊥,则上式称为限制规则。
原子集合I和NLP公式F,G之间的可满足关系|=N定义如下:
·对每个原子x∈Σ,如果x∈I,那么I|=Nx,否则,I/|=Nx;
·I|=N⊤,I⊭N⊥;
·如果I|=NF且I|=NG,那么I|=N(F,G);
·如果I|=NF或I|=NG,那么I|=N(F;G);
·如果I⊭NF,那么I|=Nnot F。
我们称I满足一条规则F←G,如果I⊭NG或I|=NF。NLP公式、规则和一个程序Π相对于原子集合I的归约按照如下方式递归定义:
·对每个原子x,xI=x;
·⊥I=⊥,⊤I=⊤;
·(F,G)I=(FI,GI);
·(F;G)I=(FI;GI);

·(F←G)I=FI←GI;
·ΠI={(F←G)I:F←G∈Π}。
注意到ΠI是一个不含not及not not联结词的程序。这样的程序也称为基本程序。类似地,若Π是一个基本程序,则Cn(Π)指满足Π的极小原子集合(又称演绎封闭)。例如,满足程序{x2←x1,x1←,x3←x3}的极小原子集为{x1,x2}。不难看出,任何一个基本程序Π的演绎封闭Cn(Π)是唯一的。
令Π为NLP程序,I为原子集合,若I=Cn(ΠI),则称I是Π的回答集。为方便,无论是CCP程序还是NLP程序Π,我们记Ans(Π)为程序Π的回答集的集合。
例5对程序Π={x←not not x},我们有Ans(Π)={∅,{x}}。因Cn(Π∅)= Cn(∅)=∅;Cn(Π{x})=Cn({x←})={x},且Π没有其它回答集。此外,不难看出程序{x←x}仅有一个回答集∅!这意味着在NLP回答集语义下,两个相邻的弱否定not并不能够直接抵消。
2.3问题的表示及简洁性
一个(二元)字符串是{0,1}组成的有穷序列。长度为n的字符串w(即w∈{0,1}n),可记为w1w2...wn,其中wi∈{0,1}(i=1,2,...,n)。一个长度为n的字符串w可看成原子集合{x1,...,xn}的子集。例如,1010表示{x1,x3},其中n=4。
一个问题L是一个字符串的集合。
定义1[6,12]给定一个问题L和逻辑程序系统C,若C中存在程序公式序列{Πn|n=1,2,...},使得对于每个字符串w∈{0,1}n,有
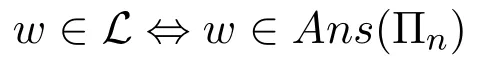
则称L可以由C表示(L∈C)。若L∈C且|Πn|≤p(n),其中p(n)为某个多项式,则称L在C中有多项式长度的表示(L∈Poly-C)。
定义2([4,6,12]) 已知C和C′是两个逻辑程序系统,若对每个问题L,
·L∈C⇔L∈C′,且
·L∈Poly-C′⇒L∈Poly-C。
则称C至少与C′一样简洁(C′≾C)。若L∈Poly-C但L/∈Poly-C′,则称L将C从C′中分离(CC′)。若C′≾C且CC′,则称C严格比C′简洁(C′≺C)。
例6为理解简洁性的直观含义,我们以命题逻辑为例进行介绍。命题公式(Propositional Formulas,PF)是建立在原子集合和连接词∨,∧,¬,←,↔上的表达式,我们可将经典地满足命题公式的原子集视为模型(或回答集)。在上述约定下:(i)PF严格比仅含联结词∨,∧,¬的合取范式(Conjunctive Normal Form,CNF)简洁。因为一般而言将命题公式等价地转换成合取范式将导致公式长度(即联结词个数)指数增长1更准确地说,我们可以找到一个问题,使得该问题在PF中可以用长度多项式增长的公式序列表示,但该问题在CNF中无法用长度多项式增长的公式序列表示。;而合取范式本身就是特殊的命题公式。(ii)合取范式与析取范式(Disjunctive Normal Form,DNF)简洁性是不可比较的。因为二者的相互等价翻译一般情况下都导致公式长度指数增长。更多的例子可见[4,6,12]。
2.4CCP及NLP与命题逻辑的等价性
我们之前提及CCP和NLP与命题逻辑是等价的,即它们有相同的表示能力,可以表示任意命题模型集/问题。本节简要讨论它们之间的等价构造。
先考虑从命题逻辑公式到程序的转换。令ϕ为一个固定字母表Σ上的CNF公式:
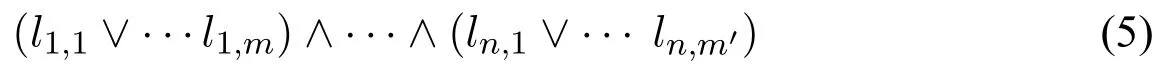
其中li,j为Σ上的经典命题逻辑文字。
·构造等价于ϕ的CCP程序。对每一个x∈Σ,引入规则

对于每个ϕ的子句(li,1∨···∨li,j),引入规则
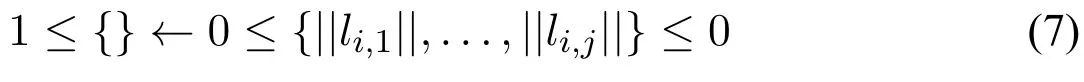
其中||li,k||是将li,k中可能出现的¬替换成not得到的文字。根据[10,13]中CCP的语义,不难看出得到的CCP程序与ϕ是等价的,即有相同的模型(回答集)。因为(6)的功能是任意选择x的真假,(7)则表达子句的约束功能,直观上,(7)的含义是若一个子句中无被满足的文字,则去掉该回答集。
·构造等价于ϕ的NLP程序。对每一个x∈Σ,引入规则

对于每个ϕ的子句(li,1∨···∨li,j),引入规则
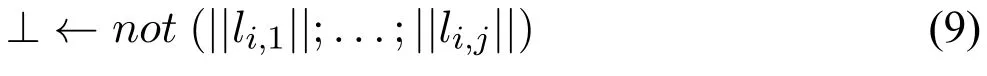
其中||li,k||是将li,k中可能出现的¬替换成not得到的文字。根据[9]中
NLP的语义,不难看出得到的NLP程序与ϕ是等价的,即有相同的模型
(回答集)。因为(8),(9)分别与(6),(7)类似,不再详细解释。
对于从CCP和NLP程序等价构造命题公式,可从语义的角度考虑。比如,令程序Π的全部回答集为{S1,...,Sn},其中Si⊆Σ为原子集{xi,1,...,xi,j}。我们很容易构造一个等价的DNF,其每个合取子句对应一个Si,具体为:
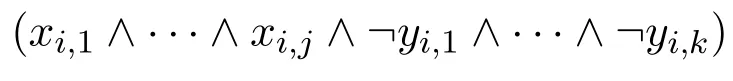
其中{yi,1,...,yi,k}=ΣSi。
由上述讨论可知,CCP和NLP与命题逻辑具有相同的表达能力。不过,从逻辑程序到命题逻辑的等价语法转换是一个较复杂的过程,有兴趣的读者可参考[2]。
3 Ferraris和Lifschitz指数增长的等价翻译
本节中我们回顾Ferraris和Lifschitz提出的从CCP程序到NLP程序的等价翻译([3]),并将通过分析指出该方法可导致翻译结果的指数增长。
对文字c1,...,cm和{1,...,m}的子集的集合X(即X⊆2{1,...,m}),定义〈c1,...,cm〉:X为以下NLP公式:

例如,X={{1,2},{2,3},{1,3}},则〈c1,c2,c3〉:X为公式(c1,c2);(c2,c3);(c1,c3)。不难看出本例中X是{1,2,3}所有元素个数≥2的子集的集合。因此,该公式直观含义为文字c1,c2,c3中至少有两个为真。换句话说,对任意原子集I,I满足该公式当且仅当I满足c1,c2,c3中至少两个文字。
值得指出的是,记法〈c1,...,cm〉:X所指的公式(10)本质上是一种对基数约束的直接枚举,其长度一般而言相对于m是指数大的。比如,根据组合原理中常用的Stirling不等式,{1,...,m}所有m/2个元素的子集的个数这说明若使用公式(10)表达c1,...,cm有一半文字为真,则公式中联结词的个数将
在上述定义的基础上,我们介绍Ferraris和Lifschitz的翻译方法如下:
1.基数约束L≤{c1,...,cm}的翻译是〈c1,...,cm〉:{Y⊆{1,...,m}:
L≤|Y|}。为方便,记L≤S的翻译为[L≤S]。
2.基数约束{c1,...,cm}≤U的翻译是not(〈c1,...,cm〉:{Y⊆{1,...,m}:
U<|Y|})。为方便,记S≤U的翻译为[S≤U]。
3.基数约束L≤S≤U的翻译是[L≤S],[S≤U]。
4.对任意CCP程序Ω,其翻译[Ω]是将Ω中每一条形如C←C1,...,Cn的
规则改写为以下p+1条规则:
·cj←not not cj,[C1],...,[Cn](1≤j≤p)
·⊥←not[C],[C1],...,[Cn].
而得到的,其中c1,...,cp是C中出现的所有正文字。
定理1([3]) 令Ω为一个CCP程序,Ω与[Ω]有相同的回答集。
此定理说明上述翻译是等价的。不过由于翻译的第1,2步涉及到联结词个数的指数增长,所以该方法可导致整体翻译长度指数增长。下面进行具体些的分析。考虑如下问题:
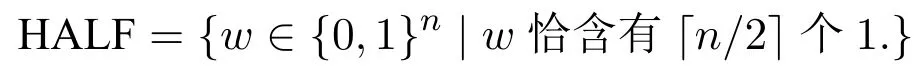
简单地说,HALF是所有那些恰有一半字符(向上取整)为1的字符串的集合。不难看出,可用CCP程序序列{Ωn|n=1,2,...,}表示HALF,其中每个Ωn仅含一条规则:根据之前的讨论,翻译所得的[Ωn]将含有个联结词。以下命题显然。
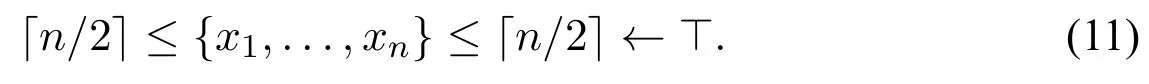
命题1存在CCP程序序列{Ωn|n=1,2,...,},其对应的NLP程序序列{[Ωn]|n=1,2,...,},每一个[Ωn]的长度
换言之,在极端情况下,Ferraris及Lifschitz的等价翻译是长度指数增长的。因此,该方法并没有对CCP与NLP的相对简洁性给出明确结论。
4 NLP至少与CCP一样简洁
本节中我们将构建从CCP到NLP的多项式等价翻译,由此证明NLP至少与CCP一样简洁。我们将首先为基数约束引入一种多项式增长的命题公式等价翻译,其核心思路来源于布尔电路设计理论([11,14])。
4.1布尔电路和命题公式
定义3([11,14]) 布尔电路是一个有向无环图,其中结点为标记了∧,∨,¬的门或布尔变元x1,x2,...或常元0,1。结点的入度(或出度)为指向(或离开)该结点的边的个数。电路的输入为布尔变元或常元0,1,其入度为0。输出为出度为0的门。但为方便,也常在输出处标上无后继的指示箭头。
简单地说,电路ψ在输入x1,...,xn下的值,记为ψ(x1,...,xn),是将输入与电路中的门通过连续布尔运算得到的结果。电路ψ的大小|ψ|为ψ中门的总数。如果ψ只有一个输出且每个门的出度为1,那么电路ψ本质上是一个命题公式。此时,可将原子集I⊆{x1,...,xm}视为输入,即xi∈I当且仅当xi=1。我们定义I|=Pψ如果ψ(I)=1,否则I⊭Pψ。不难看出,|=P本质上是经典命题逻辑的可满足关系。
图1是一个电路例子,易见ψ({x1})=ψ(1,0)=1,因此{x1}|=Pψ。又如ψ({x1,x2})=ψ(1,1)=0,所以{x1,x2}⊭Pψ。
命题2令ψ为由∨,∧,¬构成的经典命题逻辑公式,ϕ′为将ψ中的∨,∧,¬对应替换成;,not得到的NLP公式。则对于任意原子集I,
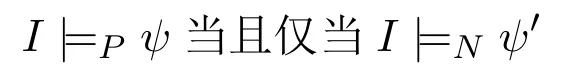
证明.据NLP公式的可满足性定义显然可得。
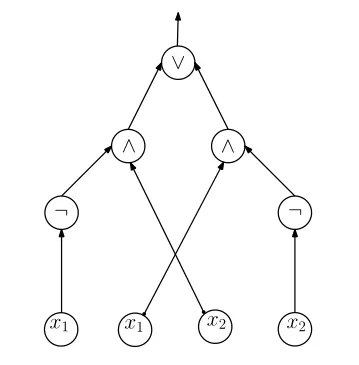
图1 :布尔电路ψ=(¬x1∧x2)∨(x1∧¬x2)

4.2基于电路方法的基数约束等价翻译
我们先将形如L≤{c1,...,cm}≤U的基数约束翻译成NLP公式:
1.对基数约束L≤{c1,...,cm},若m<L,则翻译成⊥,否则,翻译成电路
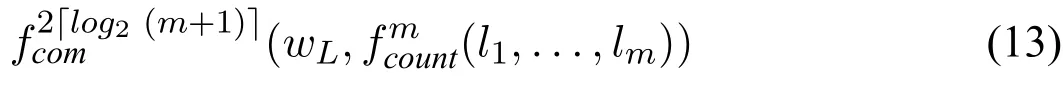
其中li=xi,如果ci是正文字(原子)xi,li=¬xi,如果ci是负文字not xi。另外,wL是L的二进制数,长度为「log2(m+1)」,不足位用0补充。特别地,构建wL时,可用xi∨¬xi表示1,xi∧¬xi表示0,其中xi是任意原子。最后,将(13)中所有∧,∨,¬门分别替换成,;not,记结果为[[L≤S]],其中S={c1,...,cm}。显然,[[L≤S]]是一个NLP公式。一个简单的基数约束1≤{x1,not x2}电路可见图2(a)。
2.对基数约束{c1,...,cm}≤U,若m<U,则翻译成⊤,否则,翻译成电路

其中li=xi,如果ci是正文字(原子)xi,li=¬xi,如果ci是负文字not xi。另外,wU是U的二进制数,长度为「log2(m+1)」,不足位用0补充。同理,构建wU时,可用xi∨¬xi表示1,xi∧¬xi表示0,其中xi是任意原子。最后,将(14)中所有∧,∨,¬门分别替换成,;not,记结果为[[S≤U]],其中S={c1,...,cm}。显然,[[S≤U]]是一个NLP公式。一个简单的基数约束{x1,not x2}≤2电路可见图2(b)。注意,[[S≤U]]以两个弱否定词not not开头,在NLP的回答集语义下,两个相邻的弱否定词并不能相互抵消。
3.对于基数约束L≤S≤U,翻译成NLP公式([[L≤S]],[[S≤U]]),也记作[[L≤S≤U]]。
命题3令I为一个原子集,对任意基数约束L≤S≤U,其中S= {c1,...,cn}是一个文字集,我们有
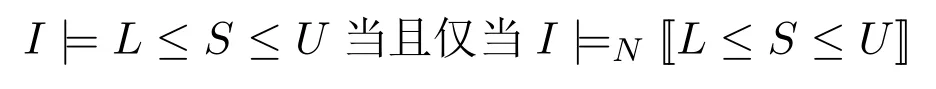
其中[[L≤S≤U]]相对于n为多项式大小,即|[[L≤S≤U]]|∈O(nk),k∈N。
证明.根据相关可满足关系定义以及对应的电路语义,不难看出:
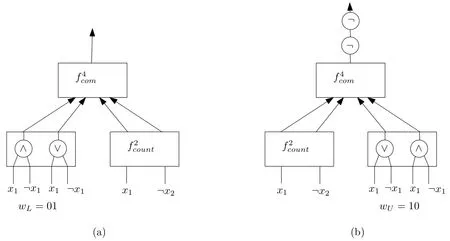
图2 :基数约束1≤{x1,not x2}和{x1,not x2}≤2的电路图示
I|=L≤S≤U当且仅当L≤v(L≤S≤U,I)≤U,
当且仅当L≤|{c∈S:I|=c}|≤U,
下面对[[L≤S≤U]]公式的大小进行分析。首先[[L≤S]]的大小由电路,电路及wL电路构成决定,根据定理2和定理3,前两个电路大小分别为O(nk1),及O(「log2(n+1)」k2),k1,k2∈N。不难看出wL电路大小为O(n),因此[[L≤S]]大小为O(nk1)+O(「log2(n+1)」k2)+O(n)。同理,容易看出[[S≤U]]的大小为O(nk1)+O(「log2(n+1)」k2)+O(n)+2。整个[[L≤S≤U]]公式由上述两部分电路合取得到,根据复杂性分析原理忽略次要量,则公式总大小为O(nk),k∈N,即多项式大小。
4.3从CCP到NLP的多项式等价翻译
利用上一小节的基数约束多项式等价翻译,我们现在构造从CCP程序到NLP程序的多项式等价翻译。
令Ω为任意CCP程序,令[[Ω]]为将Ω中每一条形如C←C1,...,Cn的规则改写为以下p+1条规则:
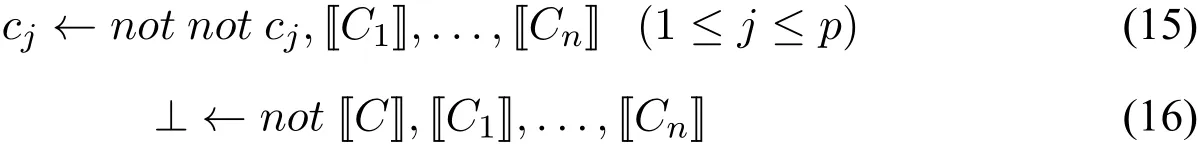
得到的NLP程序,其中c1,...,cp是C中出现的所有正文字。
命题4令Ω为任意CCP程序,则[[Ω]]相对于Ω为多项式长度,即|[[Ω]]|∈O(|Ω|k),k∈N。
证明.记Ω的长度,即其中含有基数约束的个数为n。因每条CCP规则至少含有一个基数约束,所以Ω中规则条数为O(n)。注意Ω和[[Ω]]使用固定的字母表(翻译过程不引入辅助变元),其大小记为O(1)。那么,Ω中的正文字也最多为O(1)个。由上可知,[[Ω]]中规则的个数是O(n)∗(p+1)=O(n)∗(O(1)+1)=O(n)。同时,每个规则中最多有O(n)个基数约束对应翻译得到的NLP公式,据命题3,此类NLP公式的大小是O(nk),k∈N。因此,[[Ω]]中由基数约束翻译得到NLP公式的总大小为O(n)∗O(n)∗O(nk),注意在(15)和(16)中除基数翻译外使用的not个数为O(n)∗O(1)。最终,[[Ω]]的大小,即其中含有的联结词个数为O(nk+2)+O(n)∗O(1)=O(nk+2),为多项式大小。
注意,无论Ω的组成如何,[[Ω]]总由形如(15)和(16)的规则组成。为方便,我们记(15)部分的规则为Ω1,记(16)部分的规则为Ω2,则[[Ω]]=Ω1∪Ω2。即,我们把NLP程序[[Ω]]中的规则划分成两部分,一部分是以原子开头的规则,另一部分是⊥开头的(限制)规则。对于这个区分,我们可直接应用[9]中的一个一般结论。
引理1([9]) 一个原子集I是[[Ω]]的回答集,当且仅当I是Ω1的回答集且I|=NΩ2。
引理2对任意原子集I,I|=Ω当且仅当I|=NΩ2。
证明.为方便,考虑Ω中仅有一条规则C←C1,...,Cn。此时,I|=Ω当且仅当
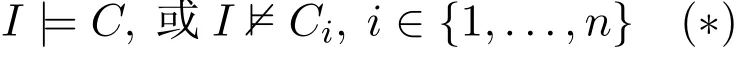
另外,I|=NΩ2当且仅当
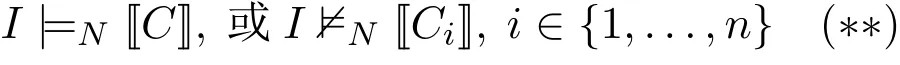
据命题3,条件(∗)与(∗∗)是等价的(当且仅当关系成立)。注意Ω含有多条规则的情形也类似。因此,命题得证。
引理3对任意两个原子集合I,I′和基数约束L≤S,则
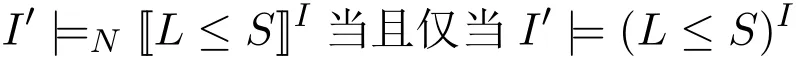
证明.根据[[L≤S]]的构造语义和归约(L≤S)I的定义,不难看出:
I′|=N[[L≤S]]I当且仅当L≤|{c∈S:I′|=NcI}|,
当且仅当L≤|{c∈S:I′|=cI}|,
当且仅当L−|{c∈S:I′|=cI且cI=⊤}|
≤|{c∈S:I′|=cI且cI=c}|,
当且仅当I′|=(L≤S)I。
引理4对任意原子集合I,基数约束S≤U,则

证明.首先,注意到本文翻译方法中,[[S≤U]]是一个以not开头的NLP公式,据2.2节中的定义,其相对于I归约要么为⊤,要么为⊥。更准确地说:

进一步地,根据命题3,I|=N[[S≤U]]当且仅当I|=S≤U。原题得证。
引理5对任意原子集I,I′,I′|=ΩI当且仅当I′|=NΩI1。
证明.为方便,考虑Ω中仅有一条规则
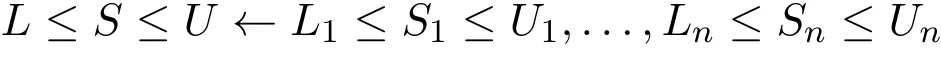
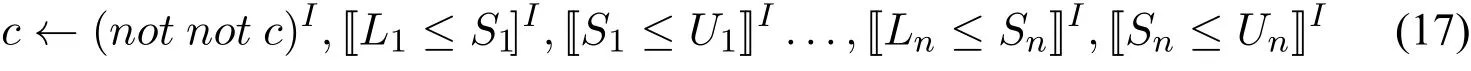
的规则组成,其中c∈S为S中的正文字。考虑以下情形:
·对任意i,1≤i≤n,都有I|=Si≤Ui。据引理4,每个[[Li≤Si]]I均为⊤。此外,如果c/∈I那么(not not c)I为⊥,I′显然满足(17)。因此,I′|=N当且仅当对任意I中正文字c
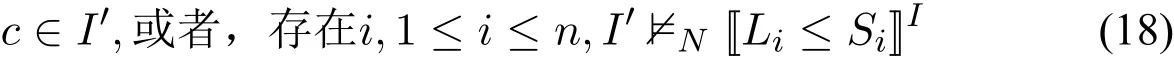
另一方面,据CCP归约的定义,ΩI由所有形如
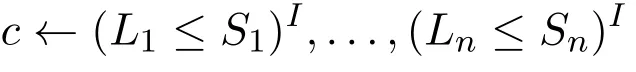
的规则组成,其中c∈S为S中的正文字。因此,I′|=ΩI当且仅当对任意I中正文字c
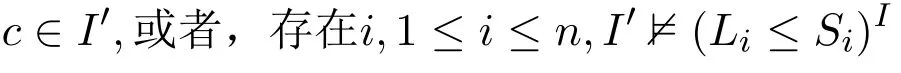
显然,据引理3,这与条件(18)是等价的。
·存在i,1≤i≤n使得I⊭Si≤Ui。据引理4,[[Li≤Si]]I为⊥,因此
I′|=NΩI1。另一方面,此情况下ΩI为空集,显然I′|=ΩI。
Ω中含有多条规则的情况类似。原题得证。
引理6对任意原子集I,I=Cn(ΩI)当且仅当I=Cn()。
证明.注意,ΩI及均为不带not的程序,Cn(·)被定义成为满足这些程序的极小原子集。据引理5,ΩI及总被相同的原子集满足,命题得证。
定理4(翻译的等价性) 令Ω为任意CCP程序,则Ω与[[Ω]]具有相同的回答集。
证明.据CCP回答集的定义,一个原子集I是Ω的回答集,当且仅当
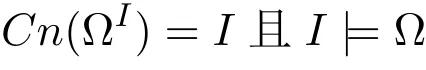
据引理6和2,上述条件等价于
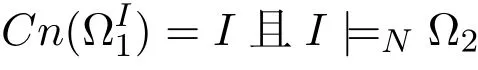

据引理1,上述条件意味着I是[[Ω]]的回答集。
定理5(主定理CCP≾NLP) NLP至少与CCP一样简洁。
证明.据定理4及命题4,每一个CCP程序Ω,都存在一个等价的NLP程序[[Ω]],使得|[[Ω]]|≤p(|Ω|),其中p是一个多项式函数。因此,对于任意CCP程序的序列{Ωn|n∈N},其中|Ωn|≤q(n),q为一个多项式函数,总是存在等价的NLP程序序列{[[Ω]]n|n∈N},使得|[[Ω]]n|≤p(q(n))。注意p(q(n))仍为多项式函数。这意味着对任何语言L,L∈Poly-CCP⇒L∈Poly-NLP。又,CCP与NLP是逻辑等价的,据定义2,NLP至少与CCP一样简洁,即CCP≾NLP。
5 结语
在本文中,我们提供了一个从CCP程序到NLP程序的多项式长度等价翻译方法。该方法改进了Ferraris和Lifschitz的结果,并意味着NLP至少与CCP一样简洁。这为进一步研究ASP以及不同类别的逻辑程序之间的关系提供了新的进展。据我们所知,CCP是否至少与NLP一样简洁依旧是开问题。典范逻辑程序(CP)作为NLP的子类,要求每条规则中的前提只能是规则元素(a,not a,not not a)合取的形式。CCP与CP之间的关系也引起了我们的兴趣,[12]指出存在PARITY问题,使得PARITY∈Poly-CCP,但PARITY/∈Poly-CP,即CCPCP。CCP似乎严格比CP简洁,但这需要我们进一步研究。
[1] G.Brewka,T.EiterandM.Truszczynski,2011,“Answersetprogrammingataglance”,Communications of the ACM,54(12):92-103.
[2] P.Ferraris,J.Lee and V.Lifschitz,2006,“A generalization of the Lin-Zhao theorem”,Annals of Mathematics and Artificial Intelligence,47(1-2):79-101.
[3] P.Ferraris and V.Lifschitz,2005,“Weight constraints as nested expressions”,Theory and Practice of Logic Programming,5(1-2):45-74.
[4] T.French,W.van der Hoek,P.Iliev and B.Kooi,2013,“On the succinctness of some modal logics”,Artificial Intelligence,197:56-85.
[5] M.Gelfond and V.Lifschitz,1988,“The stable model semantics for logic programming”,in R.Kowalski and K.Bowen(eds.),Proceedings of International Logic Programming Conference and Symposium,pp.1070-1080,Seattle,WA:MIT Press.
[6] G.Gogic,H.A.Kautz,C.H.Papadimitriou and B.Selman,1988,“The comparative linguistics of knowledge representation”,in C.Mellish(ed.),Proceedings of the 14th International Joint Conference on Artificial Intelligence,pp.862-869,San Fransisco,CA,USA:Morgan Kaufmann Publishers Inc.
[7] V.Lifschitz,2008,“What is answer set programming?”,in A.Cohn(ed.),Proceedings of the 23rd National Conference on Artificial Intelligence,Vol.3,pp.1594-1597,Chicago,IL:AAAI Press.
[8] V.Lifschitz and A.Razborov,2006,“Why are there so many loop formulas?”,ACM Transactions on Computational Logic,7(2):261-268.
[9] V.Lifschitz,L.R.Tang and H.Turner,1999,“Nested expressions in logic programs”,Annals of Mathematics and Artificial Intelligence,25:369-389.
[10] I.Niemela and P.Simons,2001,“Extending the smodels system with cardinality and weight constraints”,Logic-based Artificial Intelligence,597(14):491-521.
[11] J.E.Savage,1998,Models of Computation:Exploring the Power of Computing,Addison Wesley Longman Publishing Co.Inc.
[12] Y.Shen and X.Zhao,2014,“Canonical logic programs are succincly incomparable with propositional formulas”,in C.Baral,G.Giacomo and T.Eiter(eds.),Proceedings of the 14th International Conference on Principles of Knowledge Representation and Reasoning,Vol.3,pp.665-668,Vienna,Austria:MIT Press.
[13] P.Simons,I.Niemela and T.Soininen,2002,“Extending and implementing the stable model semantics”,Artificial Intelligence,138(1-2):181-234.
[14] I.Wegener,1987,The Complexity of Boolean Functions,John Wiley and Sons Inc.
(责任编辑:罗心澄)
Abstract
Simply speaking,succinctness means the ability of a logical system to compactly represent a problem.Recently,the study of succinctness has gained a lot of attention.In this paper,we will discuss the succinctness between two classes of logic programs,that is,cardinality constraint programs(CCP)and nested logic programs(NLP).We prove that NLP is at least as succinct as CCP,it means every CCP program can be equivalently translated into a NLP program within polynomial-size growth.This significantly improves the result of Ferraris and Lifschitz,which states that every CCP program can be equivalently translated into an exponential-size NLP program.
On the Succinctness of Logic Programs with Nested Bodies and Cardinality Constraints
Yan Zhang
Institute of Logic and Cognition,Sun Yat-sen University zhang85@mail2.sysu.edu.cn
Yuping Shen
Institute of Logic and Cognition,Sun Yat-sen University shyping@mail.sysu.edu.cn
Xishun Zhao
Institute of Logic and Cognition,Sun Yat-sen University hsszxs@mail.sysu.edu.cn
B81
A
2015-03-05;
2016-05-06
本文受国家社会科学基金青年项目《逻辑系统的简洁性研究》(14CZX058)资助。
†致谢:感谢审稿人对本文的帮助。赵希顺为本文通讯作者。
